МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
Кафедра
высшей математики.
Дисциплина «Математический анализ»
ОТЧЕТ
по курсовой работе
Тема
Решение военно-логической задачи по распределению ударной группы авиационного подразделения
г.Москва 2008г.
Словесная постановка задачи
В авиационном подразделении имеется 40 вертолетов. Планируется удар полковым вылетом по 3-м групповым целям: скоплению танков, двум дивизионам самоходной артиллерии и подразделению мотопехоты на бронетранспортерах. Необходимо найти оптимальный вариант распределения вертолетов по объектам удара и оценить его эффективность по математическому ожиданию поражаемой силы, выраженной в единицах боевого потенциала.
Боевой потенциал ударной группы приведен в табл. 1. Боевые потенциалы групповых целей приведены в табл. 2.
Таблица 1:
Количество ударных единиц
N1
|
Типы групповых целей |
Количество АСП на 1 вертолете
n1
|
Вероятность поражения единичной цели 1 ракетой.
Р1
i
|
Вероятность преодоления ПВО единичной цели.
Р2
i
|
| 40 |
Танки |
4 |
0,34 |
0,7 |
| САУ |
4 |
0,42 |
0,76 |
| БТР |
4 |
0,56 |
0,79 |
Таблица 2 :
| Групповые цели |
Количество единиц в группе
N2
i
|
Количество средств поражения на единичной цели
n2
i
|
Вероятность поражения одной ракетой одного вертолета
Р3
i
|
| Танки |
20 |
8 |
0,3 |
| САУ |
40 |
6 |
0,24 |
| БТР |
60 |
4 |
0,21 |
Процесс математического моделирования прикладной задачи условно можно разбить на три этапа:
I этап: Словесная и математическая постановка исходной задачи.
1) Словесная постановка задачи.
2) Математическая постановка задачи.
3) Исследование математической задачи на корректность.
II этап: Разработка методов решения.
1) Разработка метода решения.
2) Обоснование выбранного метода.
III этап: Проведение расчетов и анализ полученных результатов.
Итак, согласно нашего разбиения переходим к пункту 1 первого этапа:
Исходя из словесной постановки задачи (стр.2) (исходные данные были взяты гипотетические). По исходным данным определим тип задачи которую нам необходимо решить. Поставленная задача может быть представлена в виде задачи на распределение сил и средств поражения по целям.
Для решения задачи об оптимальном распределении вертолетов по групповым целям воспользуемся методом ОПТИМИЗАЦИИ АДДИТИВНОЙ ЦЕЛЕВОЙ ФУНКЦИИ.
Аддитивная целевая функция, являясь суммой частных нелинейных целевых функций, используется для оптимального распределения сил и боевых средств по задачам или объектам удара, представляющим одиночные и групповые наземные или воздушные цели. Оптимизация аддитивной функции может реализоваться в форме аналитической модели на основе метода условного экстремума.
Реклама

Далее переходим к пункту 2 первого этапа:
Математическая постановка задачи
Дадим математическую постановку задачи на следующем тактическом фоне. Имеется Sобъектов с важностями Ai
(j=1…S), по которым планируется удар N однородными средствами поражения (вертолетами). Заданы вероятности поражения каждого из объектов одним боевым средством 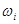 и вероятность преодоления их ПВО P2
i
(j=1…s). Требуется определить оптимальный вектор X0
=(x0
i
)s, доставляющий максимум аддитивной целевой функции ущерба и вероятность преодоления их ПВО P2
i
(j=1…s). Требуется определить оптимальный вектор X0
=(x0
i
)s, доставляющий максимум аддитивной целевой функции ущерба
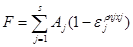
При следующих ограничениях на искомые переменные и ее параметры:
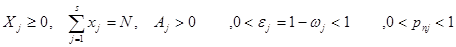
В нелинейной целевой функции xi
- наряды средств поражения по объектам удара ; Ai
– важность объектов, выражаемые в процентах или других физических единицах F – функция ущерба, представляющая собой математическое ожидание поражаемых важностей, выраженных в процентной мере или в виде конкретных физических величин (поражаемых элементарных целей, составляющих групповой объект, единицах боевого потенциала)
Максимизация функции F означает нахождение такого варианта распределения N однородных средств по S объектам удара, при котором суммарный ущерб будет наибольшим.
Для решения задачи методом условного экстремума запишем функцию Лагранжа в виде
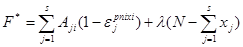
Общий результат решения можно получить по индукции на основе рассмотрения некоторого частного случая, например , S=3. Для него имеем
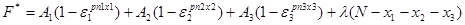
Находим частные производные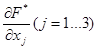 и и 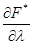 . и приравниваем их к нулю. В результате получаем систему алгебраических уравнений: . и приравниваем их к нулю. В результате получаем систему алгебраических уравнений:
 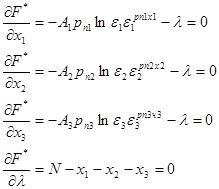 (1) (1)
Исключая неопределенный множитель Лагранжа λ, приходим к системе трех уравнений с тремя неизвестными 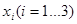
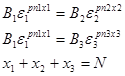 (2) (2)
Где 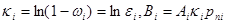 некоторые приведенные коэффициенты. Коэффициент некоторые приведенные коэффициенты. Коэффициент 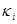 назовем приведенным коэффициентом эффективности средства поражения по i-тому объекту удара, коэффициент Bi
назовем приведенным коэффициентом важности i-ого объекта. назовем приведенным коэффициентом эффективности средства поражения по i-тому объекту удара, коэффициент Bi
назовем приведенным коэффициентом важности i-ого объекта.
Решая эту систему относительно xi
получим расчетную формулу вида
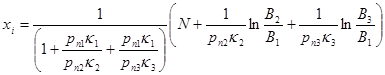 (3) (3)
Этот частный результат можно обобщить на общий случай и записать решение системы (2) в виде следующей обобщенной формулы:
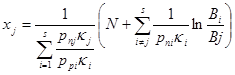 (4) (4)
В частности, для S=3 и J=1 получаем формулу (3). Возможен и другой вычислительный вариант. Сначала по формуле
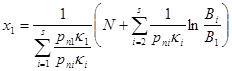 (5) (5)
Находится оптимальный наряд по первому объекту удара, а затем по системе формул
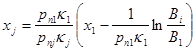 (6) (6)
Определяются оптимальные наряды по оставшимся j=2,3,,,S объектам удара. В качестве критерия правильности решения задачи выступает условие
Реклама

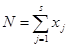
Далее переходим к пункту 3 первого этапа:
Исследование математической задачи на корректность.
Многие задачи военного содержания допускают не один , а множество вариантов решений относительно искомых переменных. Ответить на вопрос какое решение из этого множества является наилучшим без дополнительных условий, невозможно .В качестве такого дополнительного условия выступает целевая функция. Под целевой функцией будем понимать возможный конечный результат, который желательно получить путем выбора и реализации переменных, либо это количественный показатель эффективности функционирования процесса.
Итак у нас есть тактико-технические данные вертолетов и трех видов групповых целей. Найдем оптимальное распределение вертолетов по целям для нанесения максимального урона противнику
Разработка метода решения
Исходя из словесной постановки задачи, данную задачу будем решать методом выбора оптимального маршрута, с помощью аналитической оптимизации.
Задача выбора оптимального маршрута. Аналитическая оптимизация.
Решение данной задачи включает в себя следующие этапы:
1) Расчет поражающего потенциала каждой из групп целей.
2) Определение вероятности поражения, наносимого одним вертолетом каждой из групповых целей.
3) Определение важности целей выражаемых в единицах поражающего потенциала.
4) Определение условных коэффициентов эффективностей.
5) Определение обобщенных важностей целей.
6) Определение оптимального наряда вертолетов по скоплению танков.
7) Определение оптимального наряда вертолетов по дивизионам самоходных артиллерийских установок и бронетранспортерам.
8) Определение оптимального решения задачи.
Итак приступим к решению задачи поэтапно:
1) Рассчитать поражающий потенциал единичных целей по формуле
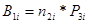
Где B1
i
-поражающий потенциал единичных целей
n2
i
- количество средств поражения на единичной цели
Р3
i
-вероятность поражения одной ракетой одного вертолета
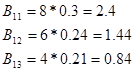
2) Определение вероятности поражения, наносимого одним вертолетом каждой из групповых целей по формуле
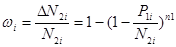
Где wi
-вероятность поражения, наносимого 1 вертолетом каждой из групповых целей
P1
i
-вероятность поражения 1 вертолетом единичной цели
N2
i
-количество единичных целей в группе
n1
-количество ракет на одном вертолете
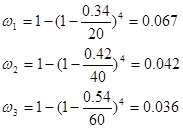
3) Определение важности целей выражаемых в единицах поражающего потенциала по формуле
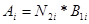
Где Аi
-важность целей в единицах боевого потенциала
N2
i
- количество единичных целей в группе
B1
i
- поражающий потенциал единичных целей
 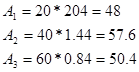
4) Определение условных коэффициентов эффективностей по формуле
 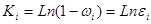
Где Ki
-условный коэффициент эффективности применения вертолетов
wi
-вероятность поражения, наносимого 1 вертолетом каждой из групповых целей
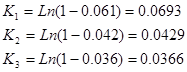
5) Определение обобщенных важностей целей по формуле
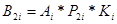
Где B2
i
-обобщенная важность групповых целей
Аi
-важность целей в единицах боевого потенциала
Ki
-условный коэффициент эффективности применения вертолетов
Р2
i
-Вероятность преодоления ПВО единичной цели.
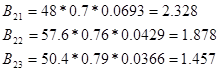
6) Определение оптимального наряда вертолетов по скоплению танков по формуле
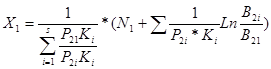
Где Р2
i
-Вероятность преодоления ПВО единичной цели.
Ki
-условный коэффициент эффективности применения вертолетов
B2
i
-обобщенная важность групповых целей
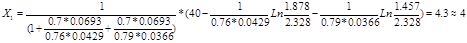
7)Определение оптимального наряда вертолетов по дивизионам самоходных артиллерийских установок и бронетранспортерам по формуле
 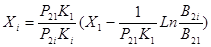
Где Р2
i
-Вероятность преодоления ПВО единичной цели.
Ki
-условный коэффициент эффективности применения вертолетов
B2
i
-обобщенная важность групповых целей
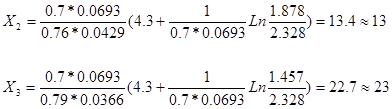
8)Определение оптимального решения задачи.
Оптимальное решение задачи представляет собой вектор
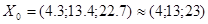
При таком использовании вертолетов величина ущерба наносимого объектам удара, максимальна и равна
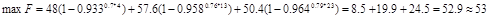
Единиц боевого потенциала, что составляет примерно 30% от суммарной боевой силы трех ударных подразделений противника. От ущерба в единицах боевого потенциала можно перейти к ущербу в единицах элементарных целей по формуле
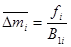
где B1
i
-поражающий потенциал единичных целей
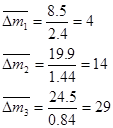
При таком использовании вертолетов будет уничтожено 4 танка, 14 самоходных артиллерийских установок и 29 бронетранспортеров.
Вывод
Некоторым недостатком аналитической модели является определение искомых переменных не в целочисленной форме. Для перехода к целочисленному ответу необходимо выполнить округление до ближайшего целого числа. В отдельных задачах одна, а может и несколько переменных могут получаться отрицательными. В этом случае такой переменной или переменным приписываются нулевые значения и выполняются повторные вычисления по сокращенной на это число системе формул(4)
Литература
1) Малявко К.Ф. «Применение математических методов в военном деле».
2) Журко М.Д. «Математические методы и основы их применения в управлении войсками».
3) Иванов П.И. «Применение методов прикладной математики в военном деле».
|