Работа №1
Случайные события
6 вариант.
Задача 1.1.
Бросают три монеты. Найти вероятность того, что только на двух монетах появится ''герб''.
Исследуемое событие А – только на двух монетах из трех будет герб. У монеты две стороны, значит всего событий при бросании трех монет будет 8. В трех случаях только на двух монетах будет герб. Вероятность события А вычислим с помощью формулы :
Р(А) = m/n = 3/8.
Ответ
: вероятность 3/8.
Задача 1.2.
Слово СОБЫТИЕ составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что буквы вынимаются в порядке заданного слова.
Испытание заключается в вынимании карточек с буквами в случайном порядке без возврата. Элементарным событием является полученная последовательность букв. Событие А состоит в получении нужного слова СОБЫТИЕ.
Элементарные события являются перестановками из 7 букв, значит, по формуле имеем n= 7!
Буквы в слове СОБЫТИЕне повторяются, поэтому не возможны перестановки, при которых слово не изменяется. Их число равно 1.
Таким образом,
Р(А) = 1/7! = 1/5040.
Ответ:
Р(А) = 1/5040.
Задача 1.3.
Как и в предыдущей задаче, найти соответствующую вероятность случая, когда заданным словом является слова АНТОНОВ ИЛЬЯ.
Эта задача решается аналогично предыдущей.
n= 11!; M = 2!*2! = 4.
Р(А) = 4/11 = 4/39916800 = 1/9979200
Ответ:
Р(А) =1/9979200.
Задача 1.4.
В урне содержится 8 черных и 6 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется:
а) 3 белых шаров;
б) меньше, чем 3, белых шаров;
в) хотя бы один белый шар.
8 ч Испытанием будет случайное вынимание 5 шаров. Элементарными
6 б событиями являются всевозможные сочетания по 5 из 14 шаров. Их число равно
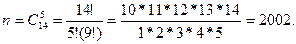
а) А1
- среди вынутых шаров 3 белых. Значит, среди вынутых шаров 3 белых и 2 черных. Используя правило умножения, получаем
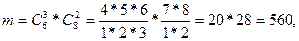 Р(А1
) = 560/2002 = 280/1001. Р(А1
) = 560/2002 = 280/1001.
б) А2
- среди вынутых шаров меньше чем 3 белых. Это событие состоит из трёх несовместных событий:
В1
- среди вынутых шаров только 2 белых и 3 черных шара,
В2
- среди вынутых шаров только один белый и 4 черных шара
В3
- среди вынутых шаров нет ни одного белого, все 5 шаров черные:
Реклама

А2
= В1
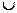 В2 В2
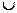 В3. В3.
Так как события В1
, В2
и В3
несовместимы, можно использовать формулу:
Р(А2
) = Р(В1
) + Р(В2
) + Р(В3
);
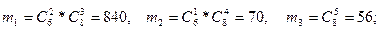
Р(А2
) = 840/2002 + 70/2002 + 56/2002 = 483/1001.
в) 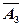 - среди вынутых шаров нет ни одного белого. В этом случае: - среди вынутых шаров нет ни одного белого. В этом случае:
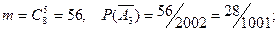
Р(А3
) = 1 - Р(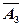 ) = 1 - 28/1001 = 973/1001. ) = 1 - 28/1001 = 973/1001.
Ответ:
Р(А1
) = 280/1001, Р(А2
) = 483/1001, Р(А3
) = 973/1001.
Задача 1.6.
В первой урне 5 белых и 7 черных шаров, а во второй урне 6 белых и и 4 черных шаров. Из первой урны вынимают случайным образом 2 шара, а из второй - 2 шара. Найти вероятность того, что среди вынутых шаров:
а) все шары одного цвета;
б) только три белых шара;
в) хотя бы один белый шар.
1 урна 2 урна Шары вынимали из обеих урн независимо. Испытаниями
5 б 6 б являются извлечение двух шаров из первой урны и двух шаров
7 ч 4 ч из второй урны. Элементарными событиями будут сочетания
_____ ______ по 2 или 2 из 12 или 10 шаров соответственно.
2 2 а) А1
- все вынутые шары одного цвета, т.е. они или все белые,
или все черные.
Определим для каждой урны всевозможные события:
В1
- из первой урны вынуты 2 белых шара;
В2
- из первой урны вынуты 1 белых и 1 черный шар;
В3
- из первой урны вынуты 2 черных шара;
С1
- из второй урны вынуты 2 белых шара;
С2
- из второй урны вынуты 1 белый и 1 черный шар;
С3
- из второй урны вынуты 2 черных шара.
Значит, А1
= 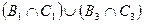 , откуда, учитывая независимость и несовместимость событий, получаем , откуда, учитывая независимость и несовместимость событий, получаем
Р(А1
) = Р(В1
) * Р(С1
) + Р(В3
) * Р(С3
).
Найдем количество элементарных событий n1
и n2
для первой и второй урн соответственно. Имеем:
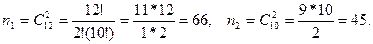
Найдем количество каждого элемента событий, определяющих следующие события:
В1
: m11
= 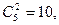 C1
: m21
= C1
: m21
= 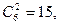
B2
: m12
=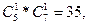 C2
: m22
= C2
: m22
= 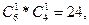
B3
: m13
=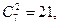 C3
: m23
= C3
: m23
= 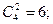
Следовательно,
Р(А1
) = 10/66 * 15/45 + 21 * 6/45 = 5/99 + 7/165 = 46/495.
б) А2
- среди извлеченных шаров только 3 белых. В этом случае
А2
= (В1
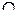 С2 С2
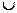 (В2 (В2
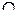 С1
); С1
);
Р(А2
) = Р(В1
) * Р(С1
) + Р(В2
) * Р(С2
)
Р(А2
) = 10/66 * 6/45 + 35/66 * 24/45 = 33/99 = 1/3.
в) А3
- среди извлеченных шаров имеется по крайней мере один белый.
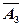 - среди извлеченных шаров нет ни одного белого шара. Тогда - среди извлеченных шаров нет ни одного белого шара. Тогда
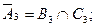
Р(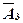 ) = Р(В3
) * Р(С3
) = 21/66 * 6/45 = 7/165; ) = Р(В3
) * Р(С3
) = 21/66 * 6/45 = 7/165;
Р(А3
) = 1 - Р(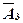 ) = 1 - 7/165 = 158/165. ) = 1 - 7/165 = 158/165.
Ответ:
Р(А1
) = 46/495, Р(А2
) = 1/3, Р(А3
) = 158/165.
Задача 1.7.
В урне содержится 5 черных и белых шаров, к ним добавляют 4 белых шара. После этого из урны случайным образом вынимают 3 шара. Найти вероятность того, что все вынутые шары белые, предполагая, что все возможные предложения о первоначальном содержании урны равновозможные.
Реклама

Здесь имеют место два вида испытаний: сначала задается первоначальное содержимое урны и затем случайным образом вынимается 3 шар, причем результат второго испытания зависит от результата первого. Поэтому используется формула полной вероятности.
событие А - случайно вынимают 3 белых шара. Вероятность этого события зависит от того, каким был первоначальный состав шаров в урне.
Рассмотрим события:
В1
- в урне было 5 белых шара;
В2
- в урне было 4 белых и 1 черный шар;
В3
- в урне было 3 белых и 2 черных шара;
В4
- в урне был 2 белый и 3 черных шара;
В5
- в урне было 1 белый и 4 черных шара.
В6
- в урне было 5 черных шара;
Общее число элементарных исходов
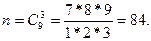
Найдем условные вероятности события А при различных условиях.
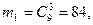 Р(А/В1
) = 1. Р(А/В1
) = 1.
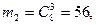 Р(А/В2
) = 56/84 = 2/3. Р(А/В2
) = 56/84 = 2/3.
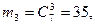 Р(А/В3
) = 35/84 = 5/12. Р(А/В3
) = 35/84 = 5/12.
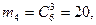 Р(А/В4
) = 5/21. Р(А/В4
) = 5/21.
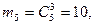 Р(А/В5
) = 5/42. Р(А/В5
) = 5/42.
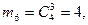 Р(А/В6
) = 1/21. Р(А/В6
) = 1/21.
Р(А) = 1 * 1/6 + 2/3 * 1/6 + 5/12 * 1/6 + 5/21 * 1/6 + 5/42 * 1/6 + 1/21 * 1/6 = 209/504.
Ответ:
Р(А) = 209/504.
Задача 1.9.
В пирамиде стоят 11 винтовок, их них 3 с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 87/100, а стреляя из винтовки без оптического прицела, - с вероятностью 52/100. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
Учитывая, что винтовки выбираются по одной, получаем 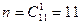 и соответственно и соответственно 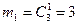 (для В1
) и (для В1
) и 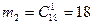 (для В2
); таким образом Р(В1
) = 3/ 11, Р(В2
) = 8/11. (для В2
); таким образом Р(В1
) = 3/ 11, Р(В2
) = 8/11.
Условные вероятности заданы в условии задачи:
Р(А/В1
) = 0,87 и Р(А.В2
) = 0,52.
Следовательно,
Р(А) = 0,87 * 3/11 + 0,52 * 8/11 = 0,615.
Ответ:
Р(А) =0,615.
Задача 1.10.
В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами изготовителями. На складе имеются электродвигатели этих заводов соответственно в количестве М1
=13, М2
=12, и М3
=17 штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно 0,91, 0,82, и 0,77. Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятность того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом - изготовителем.
Условные вероятности заданы в условии задачи: Р(А/В1
) = 0,91, Р(А/В2
) = 0,82, Р(А/В3
) = 0,77.
Аналогично предыдущей задаче найдем вероятности:
Р(В1
) = 13/42 = 0,3095; Р(В2
) = 12/42 = 0,2857; Р(В3
) = 17/42 = 0,4048;
Р(А) = 0,91 * 0,3095 + 0,82 * 0,,2857 + 0,77 * 0,4048 = 0,8276.
По формуле Байеса (1.8.) вычисляем условные вероятности событий (гипотез) В1
:
Р(В1
/А) = 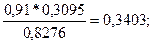
Р(В2
/А) = 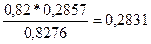
Р(В3
/А) = 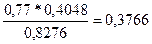
Ответ:
Р(В1
/А) = 0,3403, Р(В2
/А) = 0,2831, Р(В3
/А) = 0,3766
Работа №2
Случайные величины.
6 - вариант.
Задача 2.1.
В каждом из n независимых испытаний событие А происходит с постоянной вероятностью 0,36. Вычислить все вероятности рk
, k = 0, 1, 2, ..., 11, где k частота события А. Построить график вероятностей рk
.
Найти наивероятнейшую частоту.
Задано:
n = 11, p = 0,36, q = 1 - p = 0,64.
Найти:
р0
, р1
, р2
, ..., р11
и k.
Используя формулу Бернулли. Значение р0
вычисляем по первой из формул, а остальные вероятности рk
- по второй.
Для формулы вычисляем постоянный множитель
р/q = 0,36/ 0,64 = 0,5625, р0
= 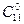 *0,360
* 0,6411
= 0,0073787. *0,360
* 0,6411
= 0,0073787.
Результаты вычислений запишем в таблице 1. Если вычисления верны, то должно выполняться равенство 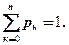
По найденным значениям вероятностей построим их график (рис. 1).
Найдем наивероятнейшую частоту по заданным условиям:
np - q 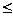 k k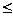 np + p, np + p,
np - q = 11 * 0,36 - 0,64 = 3,32.np + k = 4,32
Значит, наивероятнейшая частота k = 4 и, было получено ранее, значение р3
является максимальным.
Таблица 1
| k |
(n-k-1)/ k |
рk
|
k |
(n-k-1)/ k |
pk
|
0
1
2
3
4
5
|
-
11/ 1
10/ 2
9/ 3
8/ 4
7/ 5
|
0,0073787
0,0456556
0,1284066
0,2166861
0,2437719
0,1919704
|
6
7
8
9
10
11
|
6/ 6
5/ 7
4/ 8
3/ 9
2/ 10
1/ 11
|
0,1079833
0,0433861
0,0122023
0,0022879
0,0002573
0,0000131
|
 |
- |
0,9926213 |
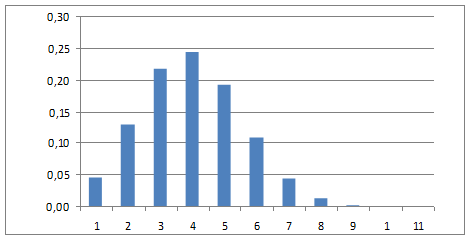
Рисунок 1 График вероятностей рk
Задача 2.2.
В каждом из n независимых испытаний событие А происходит с постоянной вероятностью 0,47. Найти вероятность того, что событие А происходит:
а) точно 330 раз;
б) меньше чем 330 и больше чем 284 раз;
в) больше чем 330 раз.
а) Задано:
п = 760, р = 0,47, М = 330.
Найти:
Р760
(330).
Используем локальную теорему Муавра - Лапласа . Находим:
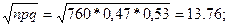
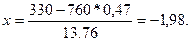
Значение функции j(x) найдем из таблицы :
j(1,98) = 0,0562, P760
(330) = 0,0562/ 13,76 = 0,00408.
б) Найти:
Р760
(284<k<330).
Используем интегральную теорему Муавра - Лапласа .
Находим: 
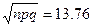
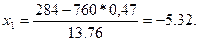
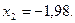
Значение функции Ф(х) найдем из таблицы :
Р760
(284<k<330) = Ф(-1,98) - Ф(-5,32) = Ф(5,32) - Ф(1,98) = 0,5 – 0,4761 = 0,0239.
в) Найти:
Р760
(330<k).
Имеем: 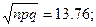 х1
= -1,98, х1
= -1,98, 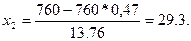
Р760
(330<k) = Р760
(330<k<760) = Ф(29,3) + Ф(1,98) = 0,5 - 0,4761 = 0,9761.
Задача 2.4.
На телефонной станции неправильное соединение происходит с вероятностью 1/800. Найти вероятность того, что среди 5600 соединений имеет место:
а) точно 2 неправильных соединений;
б) меньше чем 3 неправильных соединений;
в) больше чем 8 неправильных соединений.
а) Задано:
n = 5600, p = 1/800, k = 2.
Найти:
Р800
(2).
Получаем:
l = 5600 * 1/800 = 7.
Р800
(2) = 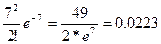 . .
б) Задано
k<3.
Найти:
Р200
(k<3).
Имеем:
l= 7.
Р800
(k<3) = Р800
(0) + Р800
(1) + Р800
(2) = 0,0223 + 0,0009 + 0,0064 = 0,0296.
в) Задано
k > 8.
Найти:
Р800
(k > 8).
Находим
l= 7.
Эту задачу можно решить проще, найти вероятность противоположного события, так как в этом случае нужно вычислить меньше слагаемых. Принимая во внимание предыдущий случай, имеем
Р800
(k>8) = 1 – Р800
(k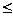 8) = 1 - Р800
(k<9) = 1 - 0,7291 = 0,2709. 8) = 1 - Р800
(k<9) = 1 - 0,7291 = 0,2709.
Задача 2.6.
Случайная величина Х задана рядом распределения.
| Х |
8 12 16 24 |
| Р |
0,11 0,14 0,50 0,25 |
Найти функцию распределения F(x) случайной величины Х и построить ее график. Вычислить для Х ее среднее значение ЕХ, дисперсию DXи моду Мо.
R = 4
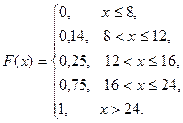
Построим график функции распределения F(x) . Среднее значение ЕХ вычисляем по формуле:
ЕХ = 8*0,11 + 12*0,14 + 16*0,5 + 24*0,25 = 16,56.
Дисперсия: Е(Х2
) = 82
*0,11 + 122
*0,14 + 162
*0,5 + 242
*0,25 = 299,2
DX = 299,2 – 16,522
= 26,2896.

График функции распределения
Задача 2.7.
Случайная величина Х задана функцией плотности вероятности
f(x) = 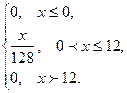
Найти функцию распределения F(x) случайной величины Х. Построить график функции f(x) и F(x). Вычислить для Х ее среднее значение ЕХ, дисперсию DX, моду Мо и медиану Ме. К = 8, R = 12.
Функцию распределения F(х) непрерывной случайной величины найдем по формуле:
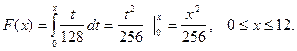
Поэтому
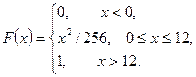
Построить графики функций f(x) и F(x). Среднее значение Х вычисляем по формуле:
ЕХ = 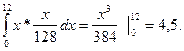
Для нахождения дисперсии Х воспользуемся формулами:
Е(Х2
) = 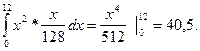
DX = 40,5 – (4,5)2
.
Из графика видно, что f(x) достигает максимума в точке х = 1/2 и, значит, Мо = 12. Для нахождения медианы Ме нужно решить уравнение х2
/ 256 = 1/2, или х2
= 128. Имеем х = ± 11,31, Ме = 11,31.

6 3
  6 12 х
График функции плотности вероятности f(x).
 6 6

3
6 12 х
График функции распределения F(х).
Работа №3.
Задача 3.1
По выборкам А и В
- составить вариационный ряд;
- вычислить относительные частоты (частости) и накопленные частости;
- построить графики вариационного ряда (полигон и гистограмму);
- составить эмпирическую функцию распределения и построить ее график;
- вычислить числовые характеристики вариационного ряда:
среднее арифметическое 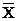 , ,
дисперсию 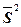 , ,
стандартное отклонение 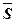 , ,
моду Мо,
медиану Ме.
Задача 3.2.
Вычислить несмещенные оценки параметров генеральной совокупности 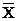 ,S2
, Sпо ,S2
, Sпо
выборкам А и В (используя результаты, полученные в задаче 3.1.), а также по первому столбцу выборки В.
Выборка А6
| 4 |
10 |
7 |
6 |
3 |
7 |
8 |
7 |
4 |
7 |
10 |
7 |
3 |
9 |
3 |
| 1 |
5 |
8 |
10 |
11 |
6 |
5 |
7 |
6 |
3 |
8 |
4 |
3 |
8 |
4 |
| 10 |
6 |
8 |
7 |
8 |
7 |
7 |
7 |
4 |
6 |
7 |
10 |
4 |
4 |
0 |
| 5 |
4 |
4 |
8 |
5 |
5 |
10 |
7 |
3 |
8 |
5 |
6 |
6 |
6 |
3 |
| 5 |
7 |
8 |
5 |
7 |
10 |
9 |
10 |
8 |
2 |
3 |
6 |
9 |
N = 73 Начало первого интервала: 0 Длина интервала: 1
Выборка В6
| 324 |
296 |
313 |
323 |
312 |
321 |
322 |
301 |
337 |
322 |
329 |
307 |
| 301 |
328 |
312 |
318 |
327 |
315 |
319 |
317 |
309 |
334 |
323 |
340 |
| 326 |
322 |
314 |
335 |
313 |
322 |
319 |
325 |
312 |
300 |
323 |
335 |
| 339 |
326 |
298 |
298 |
337 |
322 |
303 |
314 |
315 |
310 |
316 |
321 |
| 312 |
315 |
331 |
322 |
321 |
336 |
328 |
315 |
338 |
318 |
327 |
323 |
| 325 |
314 |
297 |
303 |
322 |
314 |
317 |
330 |
318 |
320 |
312 |
333 |
| 332 |
319 |
325 |
319 |
307 |
305 |
316 |
330 |
318 |
335 |
327 |
321 |
| 332 |
288 |
322 |
334 |
295 |
318 |
329 |
305 |
310 |
304 |
326 |
319 |
| 317 |
316 |
316 |
307 |
309 |
309 |
328 |
317 |
317 |
322 |
316 |
304 |
| 303 |
350 |
309 |
327 |
345 |
329 |
338 |
311 |
316 |
324 |
310 |
306 |
| 308 |
302 |
315 |
314 |
343 |
320 |
304 |
310 |
345 |
312 |
330 |
324 |
| 308 |
326 |
313 |
320 |
328 |
309 |
306 |
306 |
308 |
324 |
312 |
309 |
| 324 |
321 |
313 |
330 |
330 |
315 |
320 |
313 |
302 |
295 |
337 |
346 |
| 327 |
320 |
307 |
305 |
323 |
331 |
345 |
315 |
318 |
331 |
322 |
315 |
| 304 |
324 |
317 |
322 |
312 |
314 |
308 |
303 |
333 |
321 |
312 |
323 |
| 317 |
288 |
317 |
327 |
292 |
316 |
322 |
319 |
313 |
328 |
313 |
309 |
| 329 |
313 |
334 |
314 |
320 |
301 |
329 |
319 |
332 |
316 |
300 |
300 |
| 304 |
306 |
314 |
323 |
318 |
337 |
325 |
321 |
322 |
288 |
313 |
314 |
| 307 |
329 |
302 |
300 |
316 |
321 |
315 |
323 |
331 |
318 |
334 |
316 |
| 328 |
294 |
288 |
312 |
312 |
315 |
321 |
332 |
319 |
N = 237 Начало первого интервала: 285 Длина интервала: 7
Решение задач.
Задача 3.1.
Сначала решим задачу по выборке А. Находим: хmin
= 0 и хmax
= 11. Размах (11 - 0 + 1 = 12) довольно мал, поэтому составим вариационный ряд по значениям (табл. 1).
Таблица 1
| xi
|
ni
|
ni
/n |
Накопленные частости |
0
1
2
3
4
5
6
7
8
9
10
11
|
1
1
1
8
9
8
9
14
10
3
8
1
|
0,0137
0,0137
0,0137
0,1096
0,1233
0,1096
0,1233
0,1918
0,1370
0,0411
0,1096
0,0137
|
0,0137
0,0274
0,0411
0,1507
0,274
0,3836
0,5069
0,6987
0,8357
0,8768
0,9864
1,0001
|
| å |
73 |
1,0001 |
- |
Все относительные частоты вычисляем с одинаковой точностью. При построении графиков изображаем на оси х значения с 0 по 11 и на оси ni
/n - значения с 0 по 0,25 (рис.1 и 2).
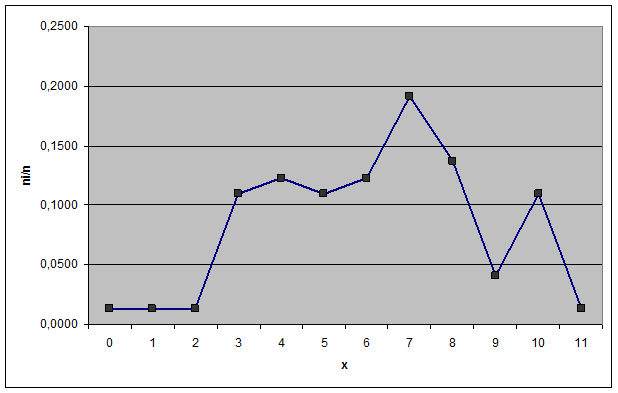
Рис. 1. Полигон вариационного ряда выборки А

Рис. 2. Гистограмма вариационного ряда выборки А.
Эмпирическую функцию распределения F*
(x) находим, используя формулу и накопленные частости, из табл. 1. Имеем:
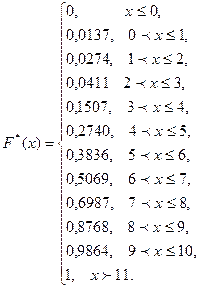
При построении графика F*
(x) откладываем значения функции в интервале от 0 до 1,2 (рис. 3).
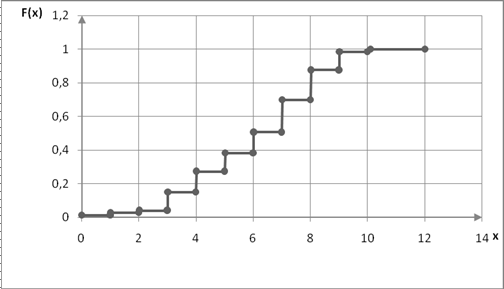
Рис.3. График эмпирической функции распределения выборки А.
Вычисление сумм для среднего арифметического и дисперсии по формулам и по вариационному ряду (см. табл. 1) оформляем в табл. 2. По максимальной частоте определяем с = 7, а шаг таблицы k = 1.
Далее по формуле вычисляем среднее арифметическое 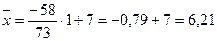 и дисперсию и дисперсию 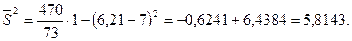
Таблица 2
| xi
|
ni
|
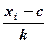 |
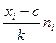 |
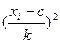 |
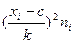 |
| 0 |
1 |
-7 |
-7 |
49 |
49 |
| 1 |
1 |
-6 |
-6 |
36 |
36 |
| 2 |
1 |
-5 |
-5 |
25 |
25 |
| 3 |
8 |
-4 |
-32 |
16 |
128 |
| 4 |
9 |
-3 |
-27 |
9 |
81 |
| 5 |
8 |
-2 |
-16 |
4 |
32 |
| 6 |
9 |
-1 |
-9 |
1 |
9 |
| 7 |
14 |
0 |
0 |
0 |
0 |
| 8 |
10 |
1 |
10 |
1 |
10 |
| 9 |
3 |
2 |
6 |
4 |
12 |
| 10 |
8 |
3 |
24 |
9 |
72 |
| 11 |
1 |
4 |
4 |
16 |
16 |
| 73 |
-58 |
470 |
Стандартное отклонение 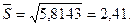 Модой Мо является значение с максимальной частотой, т.е. Мо = 7. Медианой Ме служит 37-е значение вариационного ряда: Ме = 7. Модой Мо является значение с максимальной частотой, т.е. Мо = 7. Медианой Ме служит 37-е значение вариационного ряда: Ме = 7.
Теперь по выборке В найдем хmin
= 288 и хmax
= 350. Размах (350 - 288 + 1 = 63) достаточно большой, поэтому составим вариационный ряд по интервалам значений, используя при выборке заданные начало первого интервала и длину интервала (табл.3).
Таблица 3
| Интервалы |
ni
|
ni
/n |
Накопленные частости |
285-292
292-299
299-306
306-313
313-320
320-327
327-334
334-341
341-348
348-355
|
4
8
22
36
62
50
33
16
5
1
|
0,017
0,034
0,093
0,153
0,262
0,211
0,140
0,068
0,022
0,004
|
0,017
0,051
0,144
0,295
0,557
0,768
0,907
0,975
0,996
1,000
|
| å |
237 |
1,000 |
- |
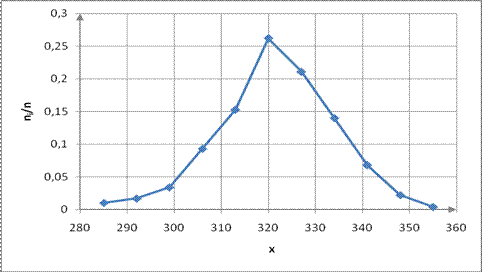
Рис. 4. Полигон вариационного ряда выборки В.
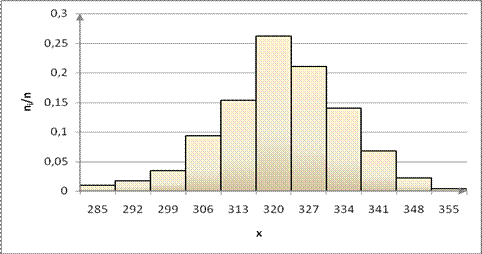
Рис. 5. Гистограмма вариационного ряда выборки В.
При построении графиков откладываем по оси х значения с 285 по 355 и по оси ni
/n - значения с 0 по 0,3(рис. 4 и 5).
Далее учитываем, что в качестве представителя каждого интервала взят его конец. Принимая за координаты точек концы интервалов и соответствующие накопленные частости (см. табл. 3) и соединяя эти точки прямыми, построим график эмпирической функции распределения (рис. 6).
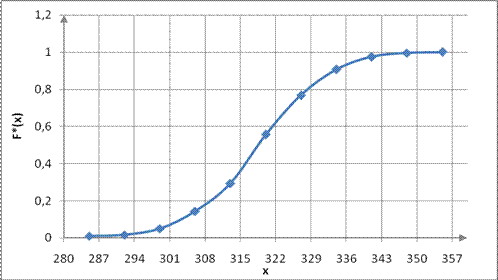
Рис. 6. График эмпирической функции распределения выборки В.
Для вычисления среднего арифметического и дисперсии по формулам и по табл. 3 определим с = 316 и k = 7. Суммы вычислим с помощью табл. 4 (табл. 4).
По формулам вычисляем среднее арифметическое 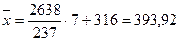 и дисперсию и дисперсию 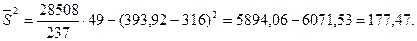
Стандартное отклонение 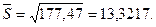 Моду находим по формуле: Моду находим по формуле:
Мо = 313 + 7×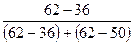 = 317,8. = 317,8.
Таблица 4
| Интервал |
Середина интервала |
ni
|
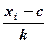 |
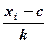 ni ni
|
(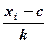 )2 )2
|
(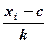 )2
ni )2
ni
|
285-292
292-299
299-306
306-313
313-320
320-327
327-334
334-341
341-348
348-355
|
289
296
303
310
317
324
331
338
345
352
|
4
8
22
36
62
50
33
16
5
1
|
-3,8
-2,8
-1,8
-0,8
0,1
1,1
2,1
3,1
4,1
5,1
|
-1114,7
-845,7
-562,7
-265,7
45,3
370,3
709,3
1062,3
1429,3
1810,3
|
14,9
8,2
3,4
0,7
0,02
1,3
4,6
9,9
17,2
26,4
|
4299,6
2416,3
1045
227,8
6,5
423,2
1519,9
3338,6
5921,3
9310
|
| å |
- |
237 |
2637,9 |
- |
28508,3 |
Медиану находим по формуле: Ме =.
Задача 3.2.
По формуле находим несмещенные оценки дисперсии и стандартного отклонения:
n = 73, S-2
= 5,8143,S2
= 73/72×5,8143 = 5,8951, S = 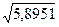 = 2,43. = 2,43.
Для выборки В имеем
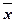 = 393,92, = 393,92, 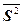 = 177,47, n = 237, S2
= 237/236×177,47 = 178,222, S = 13,35. = 177,47, n = 237, S2
= 237/236×177,47 = 178,222, S = 13,35.
Несмещенные оценки для первого столбца выборки В получаются аналогично (если эта выборка содержит мало повторяющихся элементов, вариационный ряд можно не составлять).
|