КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Планирование и прогнозирование
в условиях рынка»
на тему: Доверительные интервалы прогноза
Оценка адекватности и точности моделей
Содержание
Глава 1. Теоретическая часть. 3
Глава 2. Практическая часть. 9
Список используемой литературы.. 13
Глава
1. Теоретическаячасть
Доверительные интервалы прогноза. Оценка адекватности и точности моделей
1.1 Доверительные интервалы прогноза
Заключительным этапом применения кривых роста является экстраполяция тенденции на базе выбранного уравнения. Прогнозные значения исследуемого показателя вычисляют путем подстановки в уравнение кривой значений времени t
, соответствующих периоду упреждения. Полученный таким образом прогноз называют точечным, так как для каждого момента времени определяется только одно значение прогнозируемого показателя.
На практике в дополнении к точечному прогнозу желательно определить границы возможного изменения прогнозируемого показателя, задать "вилку" возможных значений прогнозируемого показателя, т.е. вычислить прогноз интервальный.
Несовпадение фактических данных с точечным прогнозом, полученным путем экстраполяции тенденции по кривым роста, может быть вызвано:
1. субъективной ошибочностью выбора вида кривой;
2. погрешностью оценивания параметров кривых;
3. погрешностью, связанной с отклонением отдельных наблюдений от тренда, характеризующего некоторый средний уровень ряда на каждый момент времени.
Погрешность, связанная со вторым и третьим источником, может быть отражена в виде доверительного интервала прогноза. Доверительный интервал, учитывающий неопределенность, связанную с положением тренда, и возможность отклонения от этого тренда, определяется в виде:
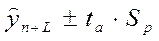 (1.1.), (1.1.),
где n- длина временного ряда;
L -период упреждения;
yn
+
L
-точечный прогноз на момент n+L;
ta
- значение t-статистики Стьюдента;
Sp
- средняя квадратическая ошибка прогноза.
Предположим, что тренд характеризуется прямой:
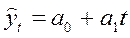
Так как оценки параметров определяются по выборочной совокупности, представленной временным рядом, то они содержат погрешность. Погрешность параметра ао
приводит к вертикальному сдвигу прямой, погрешность параметра a1
- к изменению угла наклона прямой относительно оси абсцисс. С учетом разброса конкретных реализаций относительно линий тренда, дисперсию 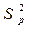 можно представить в виде: можно представить в виде:
Реклама

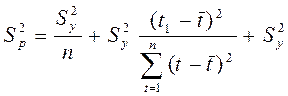 (1.2.), (1.2.),
где 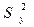 - дисперсия отклонений фактических наблюдений от расчетных; - дисперсия отклонений фактических наблюдений от расчетных;
t
1
- время упреждения, для которого делается экстраполяция;
t1
= n + L
;
t
- порядковый номер уровней ряда, t = 1,2,..., n;
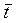 - порядковый номер уровня, стоящего в середине ряда, - порядковый номер уровня, стоящего в середине ряда, 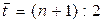
Тогда доверительный интервал можно представить в виде:
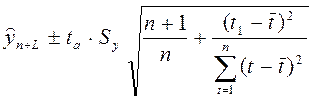 (1.3.), (1.3.),
Обозначим корень в выражении (1.3.) через К. Значение К зависит только от n и L, т.е. от длины ряда и периода упреждения. Поэтому можно составить таблицы значений К или К*= ta
K . Тогда интервальная оценка будет иметь вид:
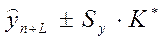 (1.4.), (1.4.),
Выражение, аналогичное (1.3.), можно получить для полинома второго порядка:
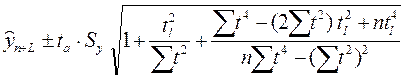 (1.5.), (1.5.),
или
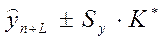 (1.6.), (1.6.),
Дисперсия отклонений фактических наблюдений от расчетных определяется выражением:
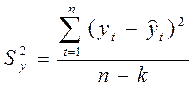 (1.7.), (1.7.),
где yt
- фактические значения уровней ряда,
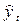 - расчетные значения уровней ряда, - расчетные значения уровней ряда,
n
- длина временного ряда,
k
- число оцениваемых параметров выравнивающей кривой.
Таким образом, ширина доверительного интервала зависит от уровня значимости, периода упреждения, среднего квадратического отклонения от тренда и степени полинома.
Чем выше степень полинома, тем шире доверительный интервал при одном и том же значении Sy
, так как дисперсия уравнения тренда вычисляется как взвешенная сумма дисперсий соответствующих параметров уравнения
Рисунок 1.1. Доверительные интервалы прогноза для линейного тренда
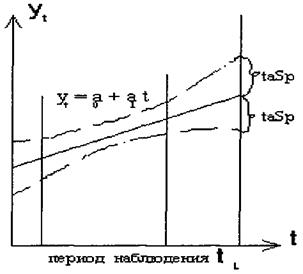
Доверительные интервалы прогнозов, полученных с использованием уравнения экспоненты, определяют аналогичным образом. Отличие состоит в том, что как при вычислении параметров кривой, так и при вычислении средней квадратической ошибки используют не сами значения уровней временного ряда, а их логарифмы.
По такой же схеме могут быть определены доверительные интервалы для ряда кривых, имеющих асимптоты, в случае, если значение асимптоты известно (например, для модифицированной экспоненты).
В таблице 1.1. приведены значения К*
в зависимости от длины временного ряда n
и периода упреждения L
для прямой и параболы. Очевидно, что при увеличении длины рядов (n
) значения К*
уменьшаются, с ростом периода упреждения L
значения К*
увеличиваются. При этом влияние периода упреждения неодинаково для различных значений n
: чем больше длина ряда, тем меньшее влияние оказывает период упреждения L
.
Таблица 1.1.
Значения К* для оценки доверительных интервалов прогноза на основе линейного тренда и параболического тренда при доверительной вероятности 0,9 (7).
Реклама

| Линейный тренд
|
Параболический тренд
|
| Длина
ряда (п)
|
Период упреждения (L)
1 2 3
|
длина ряда (п)
|
период упреждения (L)
1 2 3
|
| 7 |
2,6380 2,8748 3,1399 |
7 |
3,948 5,755 8,152 |
| 8 |
2,4631 2,6391 2,8361 |
8 |
3,459 4,754 6,461 |
| 9 |
2,3422 2,4786 2,6310 |
9 |
3,144 4,124 5,408 |
| 10 |
2,2524 2,3614 2,4827 |
10 |
2,926 3,695 4,698 |
| 11 |
2,1827 2,2718 2,3706 |
11 |
2,763 3,384 4,189 |
| 12 |
2,1274 2,2017 2,2836 |
12 |
2,636 3,148 3,808 |
| 13 |
2,0837 2,1463 2,2155 |
13 |
2,536 2,965 3,516 |
| 14 |
2,0462 2,1000 2,1590 |
14 |
2,455 2,830 3,286 |
| 15 |
2,0153 2,0621 2,1131 |
15 |
2,386 2,701 3,100 |
| 16 |
1,9883 2,0292 2,0735 |
16 |
2,330 2,604 2,950 |
| 17 |
1,9654 2,0015 2,0406 |
17 |
2,280 2,521 2,823 |
| 18 |
1,9455 1,9776 2,0124 |
18 |
2,238 2,451 2,717 |
| 19 |
1,9280 1,9568 1,9877 |
19 |
2,201 2,391 2,627 |
| 20 |
1,9117 1,9375 1,9654 |
20 |
2,169 2,339 2,549 |
| 21 |
1,8975 1,9210 1,9461 |
21 |
2,139 2,293 2,481 |
| 22 |
1,8854 1,9066 1,9294 |
22 |
2,113 2,252 2,422 |
| 23 |
1,8738 1,8932 1,9140 |
23 |
2,090 2,217 2,371 |
| 24 |
1,8631 1,8808 1,8998 |
24 |
2,069 2,185 2,325 |
| 25 |
1,8538 1,8701 1,8876 |
25 |
2,049 2,156 2,284 |
Задание 1.5. Использование адаптивных методов в экономическом прогнозировании
1. Рассчитать экспоненциальную среднюю для временного ряда курса акций фирмы ЮМ. В качестве начального значения экспоненциальной средней взять среднее значение из 5 первых уровней ряда. Значение параметра адаптации а принять равным 0,1.
Таблица 1.2.
Курс акций фирмы IBM
| t
|
yt
|
t
|
yt
|
t
|
yt
|
| 1 |
510 |
11 |
494 |
21 |
523 |
| 2 |
497 |
12 |
499 |
22 |
527 |
| 3 |
504 |
13 |
502 |
23 |
523 |
| 4 |
510 |
14 |
509 |
24 |
528 |
| 5 |
509 |
15 |
525 |
25 |
529 |
| 6 |
503 |
16 |
512 |
26 |
538 |
| 7 |
500 |
17 |
510 |
27 |
539 |
| 8 |
500 |
18 |
506 |
28 |
541 |
| 9 |
500 |
19 |
515 |
29 |
543 |
| 10 |
495 |
20 |
522 |
30 |
541 |
2. По данным задания №1 рассчитать экспоненциальную среднюю при значении параметра адаптации а
равным 0,5. Сравнить графически исходный временной ряд и ряды экспоненциальных средних, полученные при а
=0,1 и а
=0,5. Указать, какой ряд носит более гладкий характер.
3. Прогнозирование курса акций фирмы IBM осуществлялось на основе адаптивной полиномиальной модели второго порядка
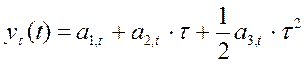 , ,
где 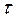 - период упреждения. - период упреждения.
На последнем шаге получены следующие оценки коэффициентов:
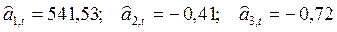
Рассчитать прогноз курса акций:
• на 1 день вперед (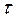 =1); =1);
• на 2 дня вперед (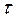 =2). =2).
Решение задания 1.5
1.
Определим
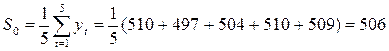
Найдем значения экспоненциальной средней при а
=0,1.
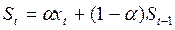 . а
=0,1 – по условию; . а
=0,1 – по условию;
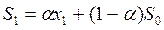 ; S1
= 0,1 х 510 + 0,9 х 506 = 506,4; ; S1
= 0,1 х 510 + 0,9 х 506 = 506,4;
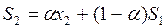 ; S2
= 0,1 х 497 + 0,9 х 506,4 = 505,46; ; S2
= 0,1 х 497 + 0,9 х 506,4 = 505,46;
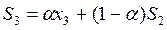 ; S3
= 0,1 х 504 + 0,9 х 505,46 = 505,31 и т.д. ; S3
= 0,1 х 504 + 0,9 х 505,46 = 505,31 и т.д.
Результаты расчетов представлены в таблице 1.3.
2.
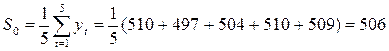
а
=0,5 – по условию.
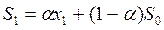 ; S1
= 0,5 х 510 + 0,5 х 506 = 508; ; S1
= 0,5 х 510 + 0,5 х 506 = 508;
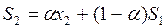 ; S2
= 0,5 х 497 + 0,5 х 508 = 502,5 и т.д. ; S2
= 0,5 х 497 + 0,5 х 508 = 502,5 и т.д.
Результаты расчетов представлены в таблице 1.3.
Таблица 1.3.
Экспоненциальные средние
| t
|
Экспоненциальная средняя
|
t
|
Экспоненциальная средняя
|
| а
=0,1
|
а
=0,5
|
а
=0,1
|
а
=0,5
|
| 1 |
506,4 |
508 |
16 |
505,7 |
513,3 |
| 2 |
505,5 |
502,5 |
17 |
506,1 |
511,7 |
| 3 |
505,3 |
503,2 |
18 |
506,1 |
508,8 |
| 4 |
505,8 |
506,6 |
19 |
507,0 |
511,9 |
| 5 |
506,1 |
507,8 |
20 |
508,5 |
517 |
| 6 |
505,8 |
505,4 |
21 |
509,9 |
520 |
| 7 |
505,2 |
502,7 |
22 |
511,6 |
523,5 |
| 8 |
504,7 |
501,4 |
23 |
512,8 |
523,2 |
| 9 |
504,2 |
500,7 |
24 |
514,3 |
525,6 |
| 10 |
503,4 |
497,8 |
25 |
515,8 |
527,3 |
| 11 |
502,4 |
495,9 |
26 |
518,0 |
532,7 |
| 12 |
502,0 |
497,5 |
27 |
520,1 |
525,8 |
| 13 |
502,0 |
499,7 |
28 |
522,2 |
538,4 |
| 14 |
502,7 |
504,4 |
29 |
524,3 |
540,7 |
| 15 |
505,0 |
514,7 |
30 |
525,9 |
540,9 |
Рисунок 1.2. Экспоненциальное сглаживание временного ряда курса акций: А – фактические данные; В – экспоненциальная средняя при альфа = 0,1; С – экспоненциальная средняя при альфа = 0,5
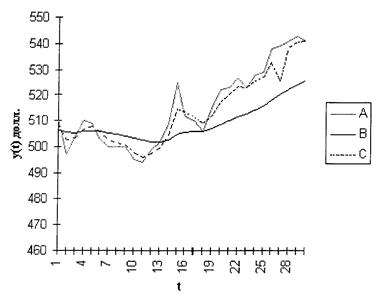
При а
=0,1 экспоненциальная средняя носит более гладкий характер, т.к. в этом случае в наибольшей степени поглощаются случайные колебания временного ряда.
3.
Прогноз по адаптивной полиномиальной модели второго порядка формируется на последнем шаге, путем подстановки в уравнение модели последних значений коэффициентов и значения 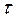 - времени упреждения. - времени упреждения.
Прогноз на 1 день вперед (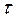 = 1): = 1):
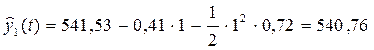 (дол.) (дол.)
Прогноз на 2 дня вперед (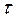 = 2): = 2):
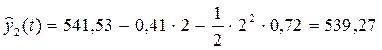 (дол.) (дол.)
1. Дуброва Т.А. Статистические методы прогнозирования в экономике: Учебное пособие / Московский государственный университет экономики, статистики и информатики. – М.: МЭСИ, 2003. – 52с.
2. Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование М.: Финансы и статистика, 2001.
3. Лукашин Ю.П. Регрессионные и адаптивные методы прогнозирования. Учебное пособие. – М.: МЭСИ, 1997.
|