Федеральное агентство по образованию
Оренбургский государственный институт менеджмента
Кафедра естественно-математических дисциплин
Реферат
по математике разделу:
Математические методы принятия управленческих решений
на тему
Сетевые модели
Выполнила студентка
группы МО-34
_________ Устинова И.В.
Проверила
_________ Кочетова Л.А.
Оренбург, 2008
Содержание
Введение. 3
1 Основные понятия сетевой модели.4
2 Обоснование привлекательности проекта по выпуску продукции.6
Заключение. 12
Список использованной литературы.. 13
До появления сетевых методов планирования работ, проектов осуществлялось в небольшом объеме. Работа была очень затратоемкой и неэффективной.
Современное планирование начинается с разбиения программы работ на операции. Определяются оценки продолжительности операций, и строится сетевая модель (график). Построение сетевой модели позволяет проанализировать все операции и внести улучшения в структуру модели до начала реализации. Строится календарный график, определяющий начало и окончание каждой операции, а также взаимосвязи с другими операциями.
Календарный график выявляет критические операции, которым надо уделять особое внимание, чтобы закончить все операции в директивный срок. Что касается некритических операций, то календарный план позволяет определить резервы времени, которые можно выгодно использовать при задержке выполнения работ или эффективном использовании как трудовых, так и финансовых ресурсов.
Сетевая модель – графическое изображение плана выполнения комплекса работ, состоящих из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого планирования лежит изображение планируемого комплекса работ в виде графа. Граф – схема, состоящая из заданных точек (вершин), соединенных системой линий. Отрезки, соединяющие вершины, называются ребрами (дугами) графа. Ориентированным называют такой граф, на котором стрелкой указаны направления всех его ребер (дуг), что позволяет определить, какая из двух его граничащих вершин является начальной, а какая – конечной. Исследование таких систем проводится методами теории графов.
Теория графов оперирует понятием пути, объединяющим последовательность взаимосвязанных ребер. Контур означает такой путь, у которого начальная вершина совпадает с конечной. Сетевой график – это ориентированный граф без контуров. В сетевом моделировании имеется два основных понятия – работа и событие.
Реклама

Работа – это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.
Фиктивная работа – это связь между результатами работ (событиями), не требующая затрат времени и ресурсов.
Событие – это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ.
Путь – это любая непрерывная последовательность (цепь) работ и событий.
Критический путь – это путь, не имеющий резервов и включающий самые напряженные работы комплекса. Работы, находящиеся на критическом пути, называются критическими.
При построении сетевых моделей необходимо соблюдать следующее правила:
1. Сеть изображается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.
2. Два соседних события могут соединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа.
3. В сети не должно быть тупиков, т.е. промежуточных событий, из которых не выходит не одна работа.
4. В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа.
5. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь.
Продолжительность выполнения работ устанавливается на основании действующих нормативов или экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором – стохастическими (вероятностными).
Основным временным параметром сетевого графика является продолжительность критического пути.
Расчет критического пути включает два этапа:
1 – прямой проход. Вычисления начинают с исходного события и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события определятся одно число, представляющее ранний срок его наступления.
2 – обратный проход. Вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления.
Реклама

Рассмотрим прямой проход:
Пусть 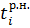 - ранний срок начала всех операций, выходящих из события - ранний срок начала всех операций, выходящих из события 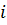 , , 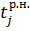 – ранний срок начала всех операций, входящих в – ранний срок начала всех операций, входящих в 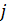 . .
Тогда 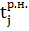 =max( =max(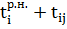 ) для всех (i,j), где ) для всех (i,j), где 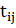 – продолжительность операций (i,j). – продолжительность операций (i,j).
Формулы для обратного прохода:
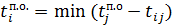 для всех операций (i,j). для всех операций (i,j).
Операция принадлежит критическому пути, если она удовлетворяет условиям:
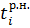 = =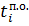
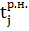 = =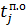
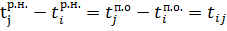 . .
Следует отметить, что критические операции должны иметь нулевой полный резерв времени, при этом свободный резерв также должен быть равен нулю.
Для финансирования проектов по строительству и наладке изготовления конкурентоспособной продукции в большинстве случаев фирме требуются инвестиции. Включение в проект материалов с оптимизацией сетевых моделей в части обоснования сроков возврата инвестиций делает проект более привлекательным и способствует принятию инвестором положительного решения.
Задача:
Предприятие решило для улучшения финансового состояния наладить выпуск конкурентоспособной продукции (мороженого). Для переоборудования цеха (участка) под выпуск этой продукции необходимо выполнить:
1) подготовку технического задания на переоборудование участка (30 дней);
2) заказ и поставку нового оборудования (60 дней);
3) заказ и поставку нового электрооборудования (50 дней);
4) демонтаж старого и установку нового оборудования (80 дней);
5) демонтаж старого и установку нового электрооборудования (80 дней);
6) переобучение персонала (30 дней);
7) испытание и сдачу в эксплуатацию оборудования для производства мороженого (20 дней).
Ожидается, что производительность после ввода новой линии составит 20 т мороженого в смену. Прибыль от реализации 1т продукции составит 0,5 тыс. р. в смену. Деньги на покупку и переоборудование участка в размере 2000 тыс. р. взяты в банке под 20 % годовых (из расчета 1500 тыс. р. на закупку оборудования и 500 тыс. р. на работы по демонтажу старого и установке нового оборудования). Затраты на проведение работ в нормальном режиме указаны в Таблице 1.
| Работа |
Нормальный режим |
| Продолжительность, дн. |
Затраты, тыс. р. |
1
2
3
4
5
6
7
|
30
60
50
90
80
30
20
|
20
40
30
70
60
25
20
|
| Итого |
360 |
265 |
Таблица 1.
Определить, через какое время может быть возвращен кредит в банк.
Решение:
1.Составим график проведения работ по пуску новой линии:
               30 60 50 90 80 30 20 30 60 50 90 80 30 20
На проведение переоборудования необходимо:
30+60+50+90+80+30+20=360 дн.
2.График можно улучшить, выполняя некоторые работы параллельно. Получим график:
 60 90 60 90
        30 30 20 30 30 20
50 80
На этом графике обозначены работы:
0,1 – подготовка технического оборудования;
1,2 – заказ и поставка нового оборудования;
1,3 – заказ и поставка нового электрооборудования;
2,4 –установка нового оборудования;
3,4 – установка нового электрооборудования;
1,4 – переобучение персонала;
4,5 – сдача в эксплуатацию новой линии.
По графику путь (0,1), (1,2), (2,4), (4,5) имеет продолжительность 200 дней; (0,1), (1,3), (3,4), (4,5) – 180 дней; (0,1), (1,4), (4,5) – 80 дней.
Критическим путем графика является путь, на котором находятся работы (0,1), (1,2), (2,4), (4,5) продолжительностью:
30+60+90+20=200 дней
График улучшится на 360 – 200=160 дней.
Определим, через какое время после начала пуска мороженого может быть возвращен в банк.
Через 200 дней после начала работ предприятие истратит 1500 тыс.р. на приобретение оборудования и 265 тыс. р. На его установку и сдачу в эксплуатацию. В наличии у предприятия останется
2000 – 1500 – 265=235 тыс. р.
  Построим графики изменения кредита в зависимости от времени получения прибыли предприятием – от выпуска мороженого. Построим графики изменения кредита в зависимости от времени получения прибыли предприятием – от выпуска мороженого.
Стоимость,
тыс.р.
 3000 3000
В (360,2400)
2000 А (0,2000)
1000 D (300,1235)
 С (200,235) С (200,235)
100 200 300 400Время, дн.
Для построения графика изменения кредита в зависимости от времени составим уравнение. Через 360 дней после выдачи банком кредита под 20 % годовых долг предприятия составит 2400 тыс. р. Поэтому известны две точки этой прямой: А(0,2000), В(360,2400). Согласно уравнению ппрямой, проходящей через две точки:
(у – 2000)/(2400 – 2000)= (x – 0)/(360 – 0)
Решая уравнение, получим:
10x – 9у+18000=0
Найдем уравнение прибыли предприятия. Известно, что через 200 дней после начала работ у предприятия осталось от кредита 235 тыс. р. Через 100 дней после начала выпуска продукции предприятие получит прибыль:
0,5*20*100=1000 тыс. р.
И в наличии у него будет
1000+235= 1235 тыс. р.
Таким образом, для нахождения уравнения прибыли имеем две точки: С (200,235), D (300,1235). Тогда уравнение прибыли:
10x – у – 1765=0
Решая совместно два найденых уравнения, определим время, через которое кредит может быть возвращен в банк. Получаем у=2471, х=424 дня.
Ответ: Через 200 дней предприятие наладит новое производство мороженого,а через 424 дня вернет кредит в банк.
Проекты по обоснованию привлекательности производства нового вида продукции важны прежде всего для предприятия, решившего начать производство нового вида продукции или изделия. Во – первых, потому что руководство должно знать сроки выполнения переоборудования и пуска новых производящих линий. Во –вторых, для администрации важно можно ли сократить сроки пуска производства новой продукции, ускорив тем самым получение прибыли. В – третьих, план содержит расчет времени необходимого для того, чтобы вернуть деньги в банк.
Такого рода проекты и все расчеты, производимые в них, важны и инвесторам или кредиторам. Ведь знание того, когда, сколько предприятие начнет получать прибыль, повышает увереность ивестора и снижает риск потери денежных средств.
Использование сетевых моделей значительно упрощает процедуры расчета времени и средств на пукс нового производства. Эти мобъясняется его широкое применение в экономическом обосновании инвестиционых проектов.
1. Колесников А.Н. Краткий курс математики для экономистов: Учебное пособие. / А.Н. Колесников. – М.: ИНФРА-М,1999. – 208 с.
2. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник / М.С. Красс, Б.П. Чупрынов. – М.: Дело, 2000. – 688 с.
3. Кремер Э.П. Высшая математика для экоомистов: Учебник / Э.П. Кремер. – М.: ИНФРА-М,2001. – 347 с.
4. Общий курс высшей математики для экономистов: Учебник / Под ред. В.И. Ермакова. – М.: ИНФРА-М, 2004. – 656 с.
|