для хранения и переработки информации.
Задача№1
Синтез реверсивного регистра сдвига.
Регистр на 10 разрядов. Использовать триггеры типа D.
Решение
Регистры представляют собой узлы цифровых систем, предназначенные для записи и хранения двоичных кодов. Например: Если необходимо сложить два числа А и В, то необходима их предварительная запись в два регистра.
Т. к. Схема регистра должна хранить двоичные цифры, а триггер предназначен для записи и хранения 0 или 1, то схема регистра должна содержать столько триггеров, сколько двоичных цифр необходимо хранить. Обычно регистры строят, используя триггеры типа D.
В качестве примера представим структуру регистра, предназначенного для записи и хранения 4-ёх разрядных двоичных чисел.
В представленной схеме выходы Q3, Q2, Q1, Q0 являются прямыми выходами регистра, в то время как необязательные выходы Q3, Q2, Q1, Q0 являются инверсными выходами регистра.
Для реализаций операций сдвига влево/вправо могут использоваться либо мультиплексоры, либо регистры. Регистр, способный сдвигать данные в обоих направлениях, называется реверсивным сдвигающим регистром (РСР).
Синтез РСР.
Выполним синтез РСР на триггерах типа D.
Составим таблицу, в которой отразим текущее и следующее состояние каждого из триггеров регистра. При этом будем полагать, что регистр 3-ёх разрядный. Так как регистр должен сдвигать либо влево, либо вправо, то в этой таблице следует в отдельном столбце записывать значение специального управляющего сигнала SL/R. Кроме того, таблица будет содержать значения, которые нужно подавать на входы D каждого из триггеров при переходе от текущего состояния в следующее состояние.
| SL/R |
t |
t+1 |
D2
|
D1
|
D0
|
| Q2
|
Q1
|
Q0
|
Q2
|
Q1
|
Q0
|
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
| 0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
| 0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
| 1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
| 1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
| 1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
Заполним диаграмму Вейча-Карно с тем, чтобы получить логические выражения для D2
, D1
, D0
.
| OO |
O1 |
11 |
1O |
OO |
O1 |
11 |
1O |
OO |
O1 |
11 |
1O |
| OO |
1 |
1 |
OO |
1 |
1 |
OO |
| O1 |
1 |
1 |
O1 |
1 |
1 |
O1 |
| 11 |
11 |
1 |
1 |
1 |
1 |
11 |
1 |
1 |
| 1O |
1O |
1O |
1 |
1 |
D2
= SL/R* Q1
D1
= SL/R* Q0
SL/R* Q2
D0
= SL/R* Q1
По полученным логическим выражениям синтезируем схему регистра.
На основе полученных логических выражений и синтезированной схемы можно получить логическое выражение и схему для i-го триггера.
Di
= SL/R* Qi - 1
SL/R* Qi + 1
На основе полученного выражения можно построить схему заданного регистра.
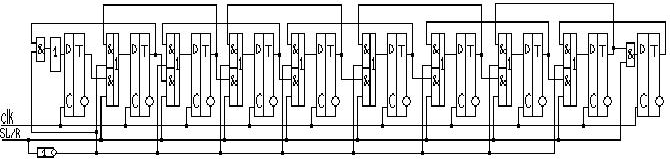
Задача№2
Синтез асинхронного двоичного счётчика, выполняющего прямой счёт, с модулем счёта равным 26, используя триггеры типа D.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Решение
Самыми простыми двоичными счётчиками являются асинхронные двоичные счётчики(АДС).Пусть к=3, тогда АДС с М=2^3 будет выглядеть:
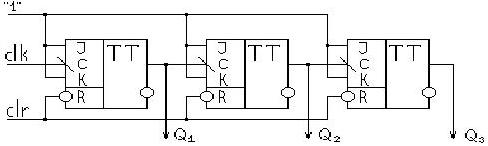
Представленная схема является схемой АДС, обеспечивающего суммирование входных импульсов ( с прымым счётом).
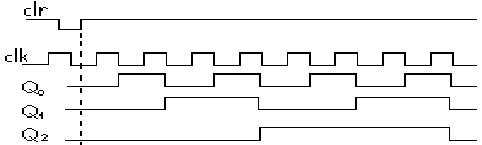
Представленная временная диаграмма поясняет работу асинхронного 3-х разрядного счётчика.
Таблица переходов для прямого счёта записывается так:
000
001
010
011
100
101
110
111
Младший триггер счётчика срабатывает по срезу входных импульсов на линии clk. Как видно из диаграммы состояние на выходе младшего триггера меняется после каждого среза входных синхроимпульсов. Так как средний триггер синхронизируется прямым выходом соседнего младшего триггера, то состояние на его выходе будет менятся при формировании среза на выходе Q0
.Так же как и на Q2
.
Преимуществом этой схемы является простота структуры,наряду с этим есть огромный недостаток: с ростом разрядности, то есть числа триггеров счётчика, возрастает суммарная задержка срабатывания самого старшего триггера счётчика, что означает необходимость уменшения частоты входных синхроимпульсов. Иначе говоря, в АДС невозможно обеспечить высокие рабочие частоты.
Если вход синхронизации соседнего старшего триггера пдключить к обратному выходу соседнего триггера, то счётчик станет вычитающим. В этом случае говорят,что имеет место обратный счёт.
Осуществим синтез заданного АДС:
Определим количество триггеров log2
26=5.
Переведём число 26 из десятичной системы счисления в двоичную: 262
= 110102
.
Изобразим схему заданного АДС:
Задача№3
Синтез синхронного двоичного счётчика, выполняющего обратный счёт, с модулем счёта равным 14, используя триггеры типа JK и логику И-НЕ.
Решение
Используем триггеры типа JK.
Определим количество триггеров.
M = log2
14 = 4
Строится таблица переходов счётчика. При этом ипсользуется таблица переходов соответствующего триггера.
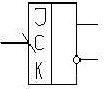
| Qt
|
Qt+1
|
J |
K |
| 0 |
0 |
0 |
* |
| 0 |
1 |
1 |
* |
| 1 |
0 |
* |
1 |
| 1 |
1 |
* |
0 |
Для счётчика с к = 14 таблица переходов будет выглядеть следующим образом:
| Q3
|
Q2
|
Q1
|
Q0
|
Q3
' |
Q2
' |
Q1
' |
Q0
' |
J3
|
K3
|
J2
|
K2
|
J1
|
K1
|
J0
|
K0
|
| 0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
* |
1 |
* |
0 |
* |
1 |
* |
| 1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
* |
0 |
* |
0 |
0 |
* |
* |
1 |
| 1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
* |
0 |
* |
1 |
1 |
* |
1 |
* |
| 1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
* |
0 |
0 |
* |
* |
0 |
* |
1 |
| 1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
* |
0 |
0 |
* |
* |
1 |
1 |
* |
| 1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
* |
0 |
0 |
* |
0 |
* |
* |
1 |
| 1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
* |
1 |
1 |
* |
1 |
* |
1 |
* |
| 0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
* |
* |
0 |
* |
0 |
* |
1 |
| 0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
* |
* |
0 |
* |
1 |
1 |
* |
| 0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
* |
* |
0 |
0 |
* |
* |
1 |
| 0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
* |
* |
1 |
1 |
* |
1 |
* |
| 0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
* |
0 |
* |
* |
0 |
* |
1 |
| 0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
* |
0 |
* |
* |
1 |
1 |
* |
| 0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
* |
0 |
* |
0 |
* |
* |
1 |
| 1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
* |
1 |
* |
1 |
* |
1 |
0 |
* |
| 1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
* |
1 |
* |
1 |
* |
1 |
* |
1 |
Строим диаграмму Вейча-Карно для функции управления J и K каждого из триггеров, используя таблицу переходов счётчика.
По диаграммам выполним минимизацию соответствующих функций, то есть получаем минимальные дизъюнктивные нормальные формы для всех сигналов J и K.
| OO |
O1 |
11 |
1O |
OO |
O1 |
11 |
1O |
OO |
O1 |
11 |
1O |
OO |
O1 |
11 |
1O |
| OO |
1 |
OO |
* |
* |
* |
* |
OO |
1 |
OO |
* |
* |
* |
* |
| O1 |
O1 |
* |
* |
* |
* |
O1 |
* |
* |
* |
* |
O1 |
1 |
| 11 |
* |
* |
* |
* |
11 |
1 |
11 |
* |
* |
* |
* |
11 |
1 |
1 |
1 |
| 1O |
* |
* |
* |
* |
1O |
1 |
1 |
1O |
1 |
1O |
* |
* |
* |
* |
| J3
= Q2
*Q1
*Q0
|
K3
= Q2
*Q1
*Q0
Q1
*Q0
|
J2
= Q1
*Q0
|
K2
= Q1
*Q0
Q3
*Q1
|
| OO |
O1 |
11 |
1O |
OO |
O1 |
11 |
1O |
OO |
O1 |
11 |
1O |
OO |
O1 |
11 |
1O |
| OO |
* |
* |
OO |
* |
* |
1 |
OO |
1 |
* |
* |
1 |
OO |
* |
1 |
1 |
* |
| O1 |
1 |
* |
* |
O1 |
* |
* |
1 |
O1 |
1 |
* |
* |
1 |
O1 |
* |
1 |
1 |
* |
| 11 |
1 |
* |
* |
11 |
* |
* |
1 |
1 |
11 |
1 |
* |
* |
11 |
* |
1 |
1 |
* |
| 1O |
1 |
* |
* |
1O |
* |
* |
1 |
1O |
1 |
* |
* |
1 |
1O |
* |
1 |
1 |
* |
 J1
= Q3
*Q0
Q2
*Q0
|
 K1
= Q0
Q3
*Q2
|
J0
= Q1
Q3
Q3
*Q2
|
K0
= 1 |
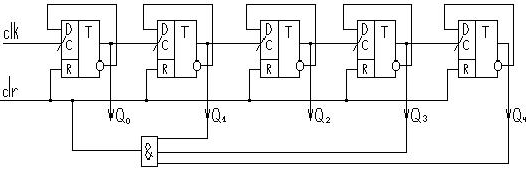
По полученным выражениям можно построить схему заданного счётчика:
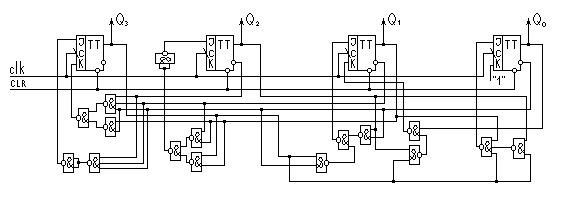
Задача№4
Синтез последовательного восьмиразрядного сумматора.
Решение
При сложении двоичных чисел на уровне I-го разряда необходимо учитывать двоичные цифры ai
и bi
, а также возможный перенос из соседнего младшего разряда. Элементарное устройство, выполняющее суммирование указанных двоичных цифр называется полным одноразрядным двоичным сумматором (ПОДС).
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Синтез ПОДС выполняется классическим путём, то есть начинается с таблицы истинности. Функции, описывающие выходы Si
и Ci
зависят от 3-х переменных ai
, bi
и ci
; поэтому таблица истинности будет выглядеть следующим образом:
| ai
|
bi
|
Ci-1
|
Si
|
Ci
|
OO |
O1 |
11 |
1O |
| 0 |
0 |
0 |
0 |
0 |
O |
1 |
1 |
| 0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
0 |
| 1 |
1 |
0 |
0 |
1 |
Si
= ai
*bi
*Ci-1
ai
*bi
*Ci-1
ai
*bi
*Ci-1
ai
*bi
*Ci-1
|
| 0 |
0 |
1 |
1 |
0 |
| 0 |
1 |
1 |
0 |
1 |
OO |
O1 |
11 |
1O |
| 1 |
0 |
1 |
0 |
1 |
O |
1 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| Ci
= ai
*bi
Ci-1
*bi
ai
*Ci-1
|
Логическая схема ПОДС в базисе И-ИЛИ-НЕ будет выглядеть следующим образом:
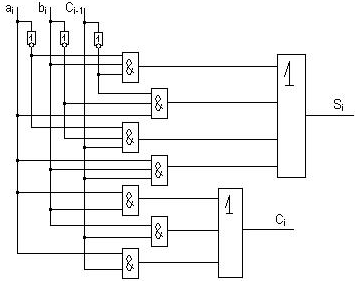
В общем случае нам необходимо складывать n-разрядные двоичные числа. Для сложения таких чисел необходимо взять n ПОДС.
Структура n-разрядного двоичного сумматора называется сумматором с последовательным распределением переноса.
Преимуществом такого сумматора является простота и низкая стоимость схемы. Недостатком является его низкое быстродействие, то есть большое время суммирования двоичных чисел.
Легко заметить, что время суммирования двоичных чисел на таком сумматоре возрастает с ростом разрядности складываемых чисел.
Если требуется быстрое суммирование двоичных чисел независимо от их разрядности, используют схему сумматора, в которой реализуется так называемый ускоренный перенос. В таком сумматоре, наряду с одноразрядными двоичными сумматорами, используется специальная схема ускоренного переноса. При этом одноразрядные сумматоры складывают двоичные цифры исходных чисел с учётом переносов вырабатываемых схемой ускоренного переноса. Так как подобная схема вычисляет все переносы одновременно (параллельно), то при суммировании чисел не приходится ждать последовательной генерации требуемых переносов.
На базе полученной схемы одноразрядного двоичного сумматора можно построить заданный сумматор. При этом нужно осуществлять загрузку двух восьмиразрядных чисел, а также сдвиг результата вправо.
Таким образом схема заданного сумматора будет выглядеть следующим образом:
|
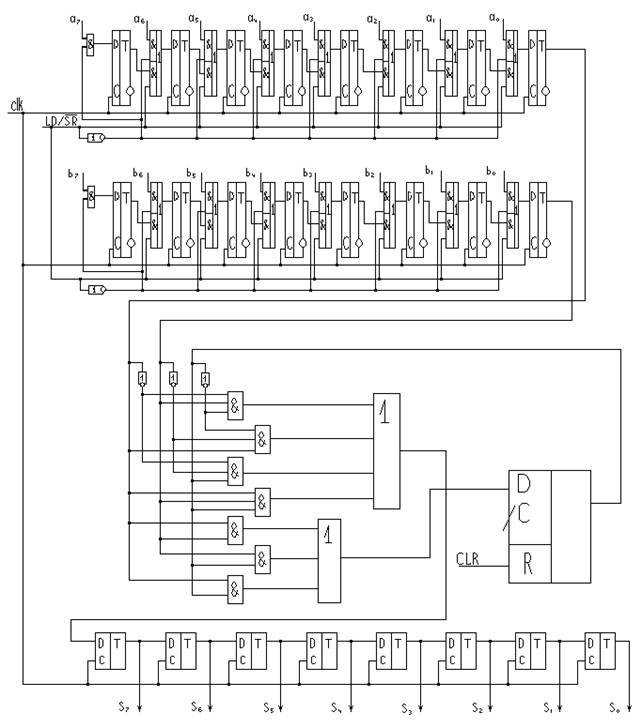
