Пономарева Т.Т., Комаров К В., Емельянов П. Ю.
РЕШЕНИЕ УРАВНЕНИЙ КОЛЕБАНИЯ СТРУНЫ
МЕТОДОМ ХАРАКТЕРИСТИК.
Известно, что решение многих задач из курса физики напрямую зависит от владения аппаратом математического анализа. Так, например, и уравнения колебания струны, которые рассматриваются как в математическом анализе, так и в курсе физики, но с разными подходами к их решению.
Существует несколько способов решения этих уравнений. При изучении уравнений колебания струны на курсе механики, студенты пользуются идеализаций, упрощений и вторым законом Ньютона. В курсе математического анализа же решение уравнений колебания струны легко решить методом характеристик или методом Даламбера.
Итак, для начала, нам нужно определить, что такое струна? Струна – это тонкая, гибкая, сильно натянутая нить с равномерно распределённой по всей длине плотностью.
Пусть струна находится под действием сильного начального натяжения 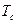 . Очевидно, что если вывести струну из положения равновесия и подвергнуть действию какой-нибудь силы, то струна начнет колебаться (см. рис. 1). . Очевидно, что если вывести струну из положения равновесия и подвергнуть действию какой-нибудь силы, то струна начнет колебаться (см. рис. 1).
Для упрощения задачи, будем ограничиваться рассмотрением малых, поперечных и плоских колебаний струны, то есть только тех колебаний, при которых отклонения точек струны от положения покоя малы. В любой момент времени все точки струны находятся в одной и той же плоскости и каждая точка колеблется, оставаясь на одном и том же перпендикуляре прямой, соответствующей состоянию покоя струны. Примем эту прямую за ось 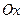 , и обозначим через , и обозначим через 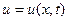 – отклонение точек струны от положения равновесия в момент времени – отклонение точек струны от положения равновесия в момент времени 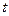 .
Итак, при каждом фиксированном значении .
Итак, при каждом фиксированном значении 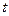 график функции график функции 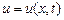 на плоскости на плоскости 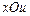 дает форму струны в момент времени дает форму струны в момент времени 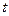 . .
Функция 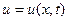 удовлетворяет дифференциальному уравнению удовлетворяет дифференциальному уравнению
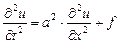 , ,
где  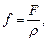 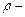 масса единицы длины, или линейная скорость струны, масса единицы длины, или линейная скорость струны, 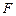 –
сила действующая на струну перпендикулярно оси абсцисс и рассчитанная на единицу длины. –
сила действующая на струну перпендикулярно оси абсцисс и рассчитанная на единицу длины.
Если внешняя сила отсутствует, то есть 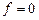 , то получим уравнение свободных колебаний струны: , то получим уравнение свободных колебаний струны:
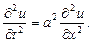
Для того чтобы определить полное движение струны, мы зададим в начальный момент времени форму и скорость струны, то есть положение её точек и их скорость в виде функций абсцисс x
этих точек. Тогда начальными условиями задачи будут:
Реклама

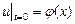 , , 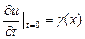 . .
Приведем уравнение
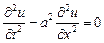
к каноническому виду и получим уравнение вида:
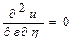 , ,
где  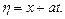
Запишем общее решение последнего уравнения:
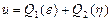 , ,
где  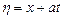 , , 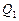 и и 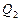 – произвольные функции. – произвольные функции.
Таким образом, общее решение дифференциального уравнения свободных колебаний запишется в виде:
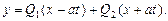
Подберем функции 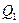 и и 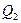 таким образом, чтобы функция таким образом, чтобы функция 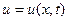 удовлетворяла приведенным начальным условиям, и тогда получим решение исходного уравнения: удовлетворяла приведенным начальным условиям, и тогда получим решение исходного уравнения:
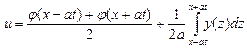
(1)
Формулу (1) называют формулой Даламбера.
Пример 1.
Найти формулу струны, определяемой уравнением 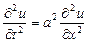 в момент времени в момент времени 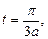 если если 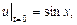 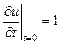 . .
Решение:
Подставляя исходные данные в формулу (1) получим:
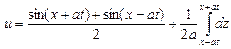
Воспользовавшись формулой суммы тригонометрических функций и одним из основных свойств интеграла:
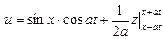 , ,
т.е.
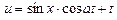 ; ;
Если 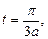 то то 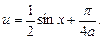
Ответ:
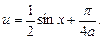
Пример 2.
Найти решение уравнения 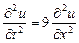 , если , если 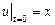 , , 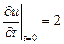 . .
Решение:
Из условий примера видно, что 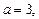 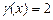 . .
Согласно формуле (1), получим:
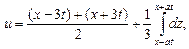
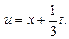
Ответ:
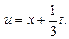
Пример 3.
Методом Даламбера найти уравнение 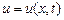 формы бесконечной струны, определяемой волновым уравнением формы бесконечной струны, определяемой волновым уравнением 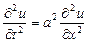 , если в начальный момент , если в начальный момент 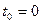 форма струны с абсциссой x
определяется соответственно заданными функциями форма струны с абсциссой x
определяется соответственно заданными функциями 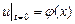 , , 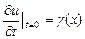 , ,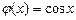 , ,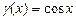 . .
Решение:
Искомая функция описывается формулой Даламбера (1)
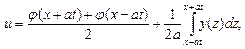 где где 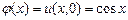 , , 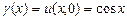 . .
Тогда
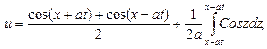
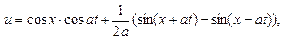
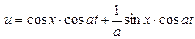 . .
Ответ:
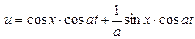 . .
Итак, после решения уравнений колебания струны методом характеристик и разбора предложенных примеров, мы видим, что эти уравнения не так сложны, как кажется на первый взгляд. Разобрав метод характеристик, каждый студент способен сам решить рассмотренные уравнения.
Также можно сказать, что благодаря знаниям основных разделов математического анализа, некоторые физические явления, уравнения, формулы из курса физики становятся понятнее и доступнее для каждого студента физико-математического факультета. Таким образом, мы пытаемся показать актуальность межпредметных связей при изучении отдельных дисциплин студентами физико-математических факультетов различных вузов.
Библиографический список:
1. Берман Г. Н. Сборник задач по курсу математического анализа. Решение типичных и трудных задач. СПб. : Издательство «Лань», 2007. - 608 с.
2. Бицадзе А. В. Уравнения математической физики: Учебник. - 2-е изд., перераб. и дополненное. - М.: Наука, Главная редакция физико-математической литературы. 1982 - 336 с.
3. С.Л. Соболев Уравнения математической физики: Учебник. - 4-е изд. - М.: Наука, Главная редакция физико-математической литературы. 1966 - 443 с.
|