Содержание.
Обоснование выбора языка программирования ……………….2 Требования к аппаратному обеспечению………………………..2 Основные принципы моделирования трёхмерных объектов....3 Алгоритм Варнока…………………………………………………….5 Описание возможностей программы…………………………….19 Интерфейс…………………………………………….………………21 6.1 Главное окно……………………………………………………21 6.2 Меню. ……………………………………………………………22 Листинг…………………………………………………………………58 Список литературы. …………………………………………………59
1. Обоснование выбора языка программирования. Представленная курсовая работа разработана среде программирования Delphi 6 от Borland. Данный программный продукт предоставляет широкие возможности для создания прикладных программ под Widows, а также Delphi является наиболее удобной средой программирования, т.к. обладает интуитивно понятным интерфейсом, мощной палитрой средств для разработки пользовательского интерфейса. В тоже время, разработка взаимодействия программа - пользователь не требует больших временных затрат, что позволяет сосредоточить внимания на реализации требуемых алгоритмов.
2. Требования к аппаратному обеспечению системы. ОС Windows 9x/NT/Me/2000/Xp. Процессор не ниже Pentium 166 Mhz. 16 Mb Ram. SVGA 800x600. HDD Free Space = 300 kb
3. Основные принципы моделирования трёхмерных объектов. Один из способов моделирования трёхмерных объектов - это описание всех поверхностей, составляющих границы объекта. В большинстве случаев объекты ограничены сложными кривыми поверхностями, для приближенного представления границ объекта можно использовать простые многоугольники. Многие простые тела, такие как, например, кубы естественным образом ограничиваются плоскостями, но даже объекты с кривыми границами, в частности цилиндр, конус или сфера, могут в достаточной мере адекватно, промоделированы большим числом плоских поверхностей. Многоугольник определяется его вершинами. Каждая вершина – это трёхмерная точка в декартовой системе координат. Во время конструирования завершенной трёхмерной сцены может возникнуть необходимость поменять местоположение одного или нескольких объектов, повращать или изменить масштаб, для этого необходимо произвести трёхмерное преобразование координат. Существует краткая математическая запись для выражения преобразования координат – матрично-векторное умножение. Трёхмерная точка представляется трёхэлементными векторами-столбцами. “Масштабирование координат точки означает умножение каждой координаты на постоянную величину. Масштабирование представляется следующей матрицей преобразования:  , где K - фактор масштабирования. , где K - фактор масштабирования. Перенос относится к передвижению объекта в новую точку с сохранением ориентации. Для переноса трёхмерной точки необходимо прибавить соответствующие смещения к X, Y, Z-координатам для получения эффекта движения. Таким образом, перенос основан на сложении двух векторов. Перенос можно выразить как матричное умножение, но для этого необходим “математический костыль” – однородные координаты. К трехмерной координате следует добавить ещё одну со значением 1:  , где X, Y, Z – координаты точки. Это представление известно как точка в однородной системе координат. Согласно этому определению можно реализовать перенос умножением этого вектора на матрицу преобразования размером 4х4, чья последняя колонка содержит параметры переноса: , где X, Y, Z – координаты точки. Это представление известно как точка в однородной системе координат. Согласно этому определению можно реализовать перенос умножением этого вектора на матрицу преобразования размером 4х4, чья последняя колонка содержит параметры переноса:  Если умножить четырёхмерный вектор V на эту матрицу, то следующий результат, который представляет перенос: Если умножить четырёхмерный вектор V на эту матрицу, то следующий результат, который представляет перенос:  Фактически используя эти искусственные однородные координаты, можно выразить все преобразования последовательностью матричных умножений. Фактически используя эти искусственные однородные координаты, можно выразить все преобразования последовательностью матричных умножений. Вращение – самое сложное преобразование координат и самое важное, потому что даёт ощущуние объёмного изображения благодаря возможности увидеть объект со всех сторон. Матрицы преобразования при вращении:  - вокруг оси OX правой системы координат, - вокруг оси OX правой системы координат,  - вокруг оси OY правой системы координат, - вокруг оси OY правой системы координат,  - вокруг оси OZ правой системы координат, где - угол поворота.” - вокруг оси OZ правой системы координат, где - угол поворота.” 4. Алгоритм Варнока. Основные идеи, на которые опирается алгоритм Варнока, обладают большой общностью. Они основываются на гипотезе о способе обработки информации, содержащейся в сцене, глазом и мозгом человека. Эта гипотеза заключается в том, что тратится очень мало времени и усилий на обработку тех областей, которые содержат мало информации. Большая часть времени и труда затрачивается на области с высоким информационным содержимым. В качестве примера рассмотрим поверхность стола, на которой нет ничего, кроме вазы с фруктами. Для восприятия цвета, фактуры и других аналогичных характеристик всей поверхности стола много времени не нужно. Все внимание сосредоточивается на вазе с фруктами. В каком месте стола она расположена? Велика ли она? Из какого материала сделана: из дерева, керамики, пластика, стекла, металла? Каков цвет вазы: красный, синий, серебристый; тусклый или яркий и т. п.? Какие фрукты в ней лежат: персики, виноград, груши, бананы, яблоки? Каков цвет яблок: красный, желтый, зеленый? Есть ли у яблока хвостик? В каждом случае, по мере сужения сферы интереса, возрастает уровень требуемой детализации. Далее, если на определенном уровне детализации на конкретный вопрос нельзя ответить немедленно, то он откладывается на время для последующего рассмотрения. В алгоритме Варнока и его вариантах делается попытка извлечь преимущество из того факта, что большие области изображения однородны, например поверхность стола в приведенном выше примере. Такое свойство известно как когерентность, т. е. смежные области (пиксели) вдоль обеих осей х и у имеют тенденцию к однородности. Поскольку алгоритм Варнока нацелен на обработку картинки, он работает в пространстве изображения. В пространстве изображения рассматривается окно и решается вопрос о том, пусто ли оно, или его содержимое достаточно просто для визуализации. Если это не так, то окно разбивается на фрагменты до тех пор, пока содержимое подокна не станет достаточно простым для визуализации или его размер не достигнет требуемого предела разрешения. В последнем случае информация, содержащаяся в окне, усредняется, и результат изображается с одинаковой интенсивностью или цветом. Устранение лестничного эффекта можно реализовать, доведя процесс разбиения до размеров, меньших, чем разрешение экрана на один пиксель, и усредняя атрибуты подпикселей, чтобы определить атрибуты самих пикселей. Конкретная реализация алгоритма Варнока зависит от метода разбиения окна и от деталей критерия, используемого для того, чтобы решить, является ли содержимое окна достаточно простым. В оригинальной версии алгоритма Варнока каждое окно разбивалось на четыре одинаковых подокна. На рис. 1 показан результат простейшей реализации алгоритма Варнока. Здесь окно, содержимое которого слишком сложно изображать, разбито на четыре одинаковых подокна. Окно, в котором что-то есть, подразбивается далее до тех пор, пока не будет достигнут предел разрешения экрана.
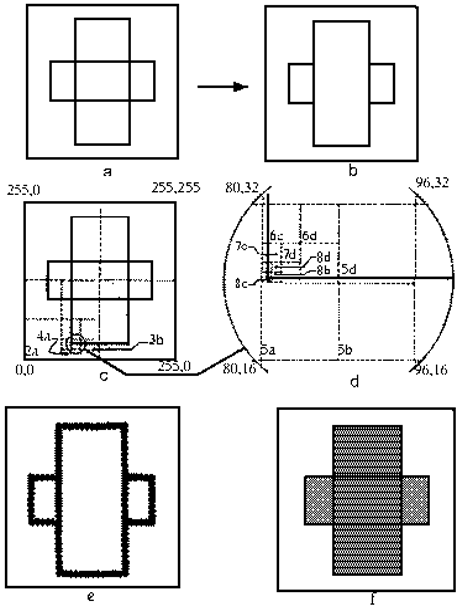 рис. №1 “Пример использования алгоритма Варнока”
На рис. 1, a показана сцена, состоящая из двух простых многоугольников. На рис. 1, b показан результат после удаления невидимых линий. Заметим, что горизонтальный прямоугольник частично экранирован вертикальным. На рис. 1, c и d показан процесс разбиения окон на экране с разрешением 256х256. Поскольку 256 = 2^8, требуется не более восьми шагов разбиения для достижения предела разрешения экрана. Пусть подокна рассматриваются в следующем порядке: нижнее левое, нижнее правое, верхнее левое, верхнее правое. Будем обозначать подокна цифрой и буквой,' цифра – это номер шага разбиения, а буква – номер квадранта. Тогда для окна 1а подокна 2а, 4а, 4с, 5а, 5b оказываются пустыми и изображаются с фоновой интенсивностью в процессе разбиения. Первым подокном, содержимое которого не пусто на уровне пикселей, оказывается 8а. Теперь необходимо решить вопрос о том, какой алгоритм желательно применить: удаления невидимых линий или удаления невидимых поверхностей. Если желательно применить алгоритм удаления невидимых линий, то пиксель, соответствующий подокну 8а, активируется, поскольку через него проходят видимые ребра. В результате получается изображение видимых ребер многоугольников в виде последовательности точек размером с пиксель каждая (рис. 1, е). Следующее рассмотрение окна, помеченного как 8d на рис. 1, d, лучше всего проиллюстрирует различие между реализациями алгоритмов удаления невидимых линий и поверхностей. В случае удаления невидимых линий окно 8d размером с пиксель не содержит ребер ни одного многоугольника сцены. Следовательно, оно объявляется пустым и изображается с фоновой интенсивностью или цветом. Для алгоритма удаления невидимых поверхностей проверяется охват этого окна каждым многоугольником сцены. Если такой охват обнаружен, то среди охватывающих пиксель многоугольников выбирается ближайший к точке наблюдения на направлении наблюдения, проходящем через данный пиксель. Проверка проводится относительно центра пикселя. Затем этот пиксель изображается с интенсивностью или цветом ближайшего многоугольника. Если охватывающие многоугольники не найдены, то окно размером с пиксель пусто. Поэтому оно изображается с фоновым цветом или интенсивностью. Окно 8d охвачено вертикальным прямоугольником. Поэтому оно изображается с цветом или интенсивностью этого многоугольника. Соответствующий результат показан на рис. 1, f. Возвратившись к рассмотрению окна 8а на рис. 1, d, покажем, как включить в алгоритм удаления невидимых поверхностей устранение лестничного эффекта. Разбиение этого окна дает четыре подокна с размерами, меньшими, чем размеры пикселя. Только одно из этих подокон – правое верхнее – охвачено многоугольником. Три других пусты. Усреднение результатов для этих четырех подпикселей показывает, что окно 8а размером с пиксель нужно изображать с интенсивностью, равной одной четверти интенсивности прямоугольника. Аналогично пиксель 8Ь следует высвечивать с интенсивностью, равной половине интенсивности прямоугольника. Конечно, окна размером с пиксель можно разбивать более одного раза, чтобы произвести взвешенное усреднение характеристик. Процесс подразбиения порождает для подокон структуру данных, являющуюся деревом, которое показано на рис. 2 (В алгоритме Варнока впервые была реализована такая структура данных, как кватернарное дерево). Корнем этого дерева является визуализируемое окно. Каждый узел изображен прямоугольником, содержащим координаты левого нижнего угла и длину стороны подокна. Предположим, что подокна обрабатываются в следующем порядке: abcd, т. е. слева направо на каждом уровне разбиения в дереве. На рис. 2 показан активный путь по структуре данных дерева к окну 8а размером с пиксель. Активные узлы на каждом уровне изображены толстой линией. Рассмотрение рис. 1 и 2 показывает, что на каждом уровне все окна слева от активного узла пусты. Поэтому они должны были визуализироваться ранее с фоновым значением цвета или интенсивности. Все окна справа от активного узла на каждом уровне будут обработаны позднее, т. е. будут объявлены пустыми или будут подразделены при обходе дерева в обратном порядке.
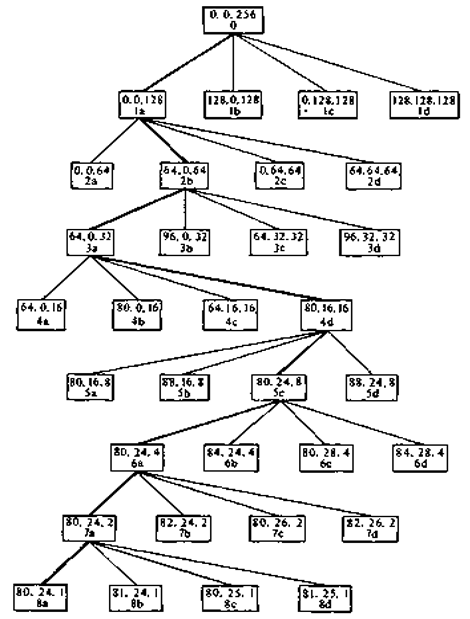 рис. №2 “ Дерево разбиения окон”
При помощи изложенного алгоритма можно удалить либо невидимые линии, либо невидимые поверхности. Однако простота критерия разбиения, а также негибкость способа разбиения приводят к тому, что количество подразбиений оказывается велико. Можно повысить эффективность этого алгоритма, усложнив способ и критерий разбиения. Например, с использованием прямоугольной объемлющей оболочки многоугольника. Заметим, что подокна при этом могут быть неквадратными. Этот способ можно рекурсивно применить к любому многоугольнику, который полностью охвачен каким-нибудь окном или подокном. Если в окне содержится только один многоугольник и если он целиком охвачен этим окном, то его легко изобразить, не проводя дальнейшего разбиения. Такой способ разбиения полезен, в частности, при минимизации числа разбиений для простых сцен. Однако с ростом сложности сцены его преимущество сходит на нет. Для рассмотрения более сложных критериев разбиения будет полезно определить способы расположения многоугольников относительно окна. Назовем многоугольник: внешним, если он находится целиком вне окна;
внутренним, если он находится целиком внутри окна;
пересекающим, если он пересекает границу окна;
охватывающим, если окно находится целиком внутри него. На рис. 4 показаны примеры всех этих типов многоугольников. 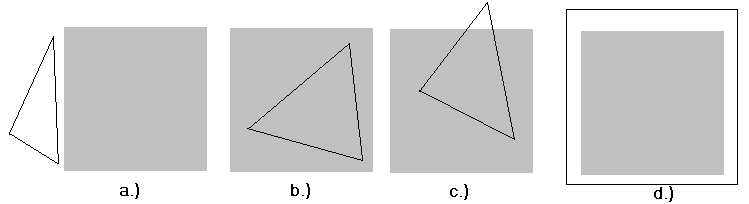 Рис. №3. “Типы многоугольников: внешний (a), внутренний (b), пересекающий (c), охватывающий (d).”
Используя эти определения, можно предложить следующие правила обработки окна:
Для каждого окна: Если все многоугольники сцены являются внешними по отношению к окну, то это окно пусто. Оно изображается с фоновой интенсивностью или цветом без дальнейшего разбиения.
Если внутри окна находится только один многоугольник, то площадь окна вне этого многоугольника заполняется фоновым значением интенсивности или цвета, а сам многоугольник заполняется соответствующим ему значением интенсивности или цвета.
Если только один многоугольник пересекает окно, то площадь окна вне многоугольника заполняется фоновым значением интенсивности или цвета, а та часть пересекающего многоугольника, которая попала внутрь окна, заполняется соответствующей ему интенсивностью или цветом.
Если окно охвачено только одним многоугольником и если в окне нет других многоугольников, то окно заполняется значением интенсивности или цвета, которое соответствует охватывающему многоугольнику.
Если найден, по крайней мере, один охватывающий окно многоугольник и если этот многоугольник расположен ближе других к точке наблюдения, то окно заполняется значением интенсивности или цвета, которое соответствует охватывающему многоугольнику.
В противном случае проводится разбиение окна. Первые четыре из этих критериев касаются ситуаций, в которых участвуют один прямоугольник и окно. Они используются для сокращения числа подразбиений. Пятое правило является ключом к решению задачи удаления невидимых поверхностей. В нем речь идет о поиске такого охватывающего многоугольника, который находился бы ближе к точке наблюдения, чем все остальные многоугольники, связанные с этим окном. Очевидно, что этот многоугольник будет закрывать или экранировать все остальные многоугольники, связанные с окном. Поэтому в сцене будут фигурировать именно его визуальные характеристики. Для реализации этих правил требуются методы определения способа расположения многоугольника относительно окна. В случае прямоугольных окон можно воспользоваться минимаксными или габаритными, с объемлющей прямоугольной оболочкой, тестами для определения, является ли многоугольник внешним по отношению к окну. В частности, если xЛ, xП, yН, yВ определяют четыре ребра окна, а xmin, xmax, ymin, ymax – ребра прямоугольной объемлющей оболочки многоугольника, то этот многоугольник будет внешним по отношению к окну, если выполняется любое из следующих условий: xmin > xП, xmax < xЛ, ymin > yВ, ymax < yН Кроме того, многоугольник является внутренним по отношению к окну, если его оболочка содержится внутри этого окна, т. е. если xmin >= xЛ, xmax <= xП, ymin >= yН, ymax < yВ Можно воспользоваться простой подстановкой для проверки пересечения окна многоугольником. Координаты вершин окна подставляются в пробную функцию, заданную уравнением прямой, несущей ребро многоугольника. Если знак этой пробной функции не зависит от выбора вершины окна, то все его вершины лежат по одну сторону от несущей прямой и на указанной прямой нет точек пересечения. Если же эти знаки различны, то многоугольник пересекает окно. Если ни одно из ребер многоугольника не пересекает окна, то этот многоугольник либо является внешним по отношению к окну, либо охватывает его. Если уравнение прямой, проходящей через две вершины P1(x1, y1) и P2(x2, y2), имеет вид у = тх + b, то пробная функция (T.F. – test function) такова: T.F. = у – mх – b , где  , x2 – x10, b = у1 – mх1. , x2 – x10, b = у1 – mх1. Простым габаритным тестом с прямоугольной оболочкой, который рассматривался выше, нельзя идентифицировать все виды внешних многоугольников. Для этого нужны более сложные тесты. Особый интерес представляют тест с бесконечной прямой и тест с подсчетом угла. В обоих тестах предполагается, что внутренние и пересекающие многоугольники уже были идентифицированы. Оба теста могут быть использованы для определения внешних и охватывающих многоугольников. В тесте с бесконечной прямой проводится луч из любой точки окна, например из угла в бесконечность. Подсчитывается число пересечений этого луча с заданным многоугольником. Если это число четное (или нуль), то многоугольник внешний; если же оно нечетное, то многоугольник охватывает окно. Если луч проходит через вершину многоугольника, то результат неопределен. Эта неопределенность устраняется, если считать касание за два пересечения, а протыкание – за одно. Изменение угла наклона луча тоже позволяет устранить неопределенность. Теперь рассмотрим тест с подсчетом угла. Совершим обход по ребрам многоугольника по или против часовой стрелки. При этом просуммируем углы, образованные лучами, начинающимися в любой точке окна и проходящими через начало и конец проходимого в данный момент ребра многоугольника. Часто удобной точкой является центр окна. Получаемая сумма углов интерпретируется следующим образом: Сумма = 0, многоугольник, внешний по отношению к окну.
Сумма = ± 360 n, многоугольник охватывает окно n раз (простой многоугольник (не имеющий самопересечений) может охватить точку только один раз). Практическое вычисление этой суммы значительно упрощается, если учесть, что точность вычисления каждого угла не обязана быть высокой. Фактически нужная точность получается, если считать только целые октанты (приращения по 45°), покрытые отдельными углами. Техника здесь напоминает ту, что использовалась для кодирования концов отрезка при отсечении. Пронумеруем октанты числами от 0 до 7 против часовой стрелки. Число целых октантов, покрытых углом, равно разности между номерами октантов, в которых лежат концы его ребер. Предлагается следующий алгоритм: = (номер октанта, в котором лежит второй конец ребра) – (номер октанта, в котором лежит первый конец ребра) if > 4 then = – 8
if < – 4 then = + 8
if = 0 then ребро многоугольника расщепляется ребром окна, и процесс повторяется с парой полученных отрезков. Суммируя вклады от отдельных ребер, получаем: 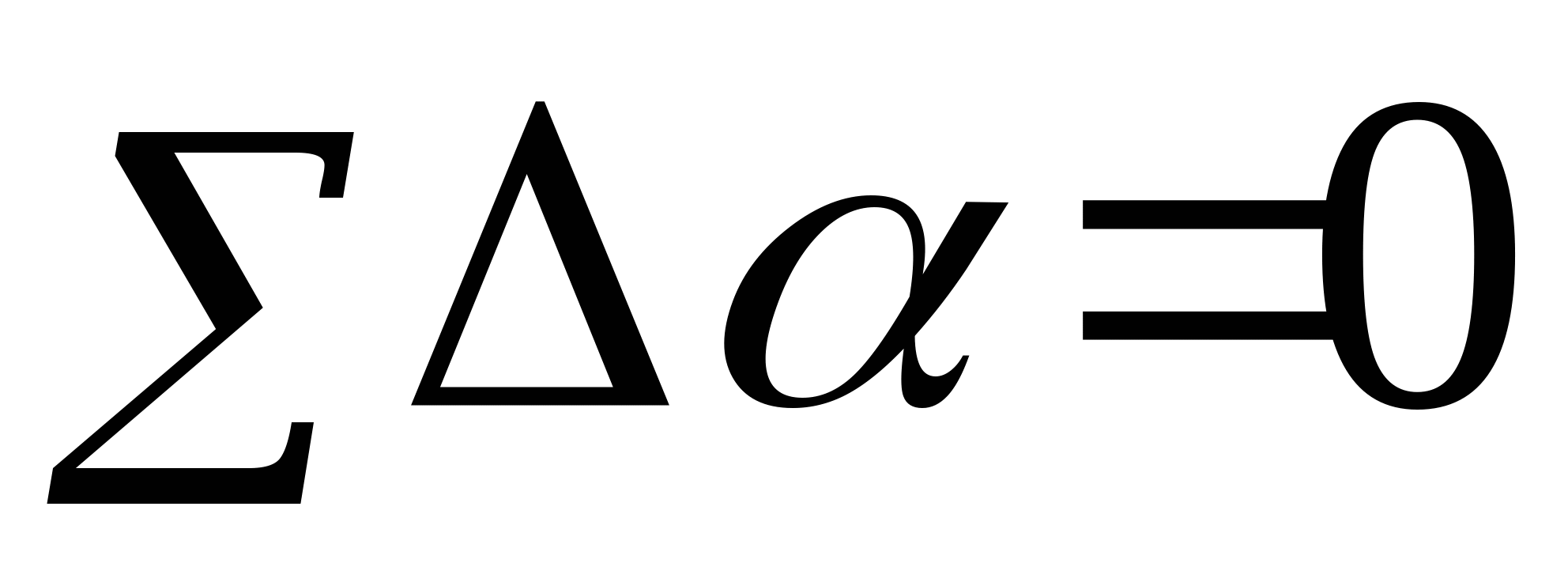 многоугольник, внешний по отношению к окну. многоугольник, внешний по отношению к окну. 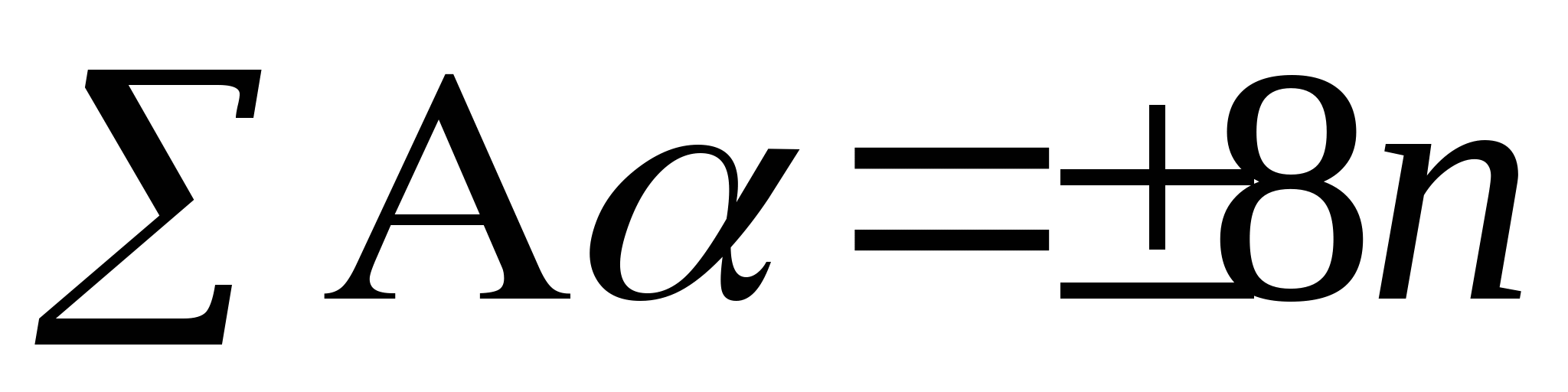 многоугольник охватывает окно. многоугольник охватывает окно. Иерархическое использование методов, основанных на изложенных вычислительных приемах, дает дополнительный выигрыш. Если реализуется только простейший алгоритм Варнока, то нет смысла определять внутренние или пересекающие многоугольники. Разбиения будут постоянно превращать такие многоугольники во внешние или охватывающие. Все нестандартные ситуации разрешаются на уровне пикселей. В этом простом алгоритме для определения пустых окон достаточно пользоваться только тестом с прямоугольной объемлющей оболочкой. Если этот простой тест дает отрицательный результат, то алгоритм разбивает окно вплоть до достижения уровня пикселей. Более сложный алгоритм, обсуждавшийся выше, делает попытку определить способ расположения многоугольника относительно окна больших размеров, чтобы избежать его подразбиения. Такие тесты требуют больших вычислительных затрат. Следовательно, существует зависимость между затратами, связанными с процессом разбиения окон, и затратами, связанными с ранним определением окон, готовых к визуализации. Более сложный алгоритм должен реализовать тестирование каждого окна в следующем порядке. Провести проверку при помощи простого теста с прямоугольной оболочкой для определения как можно большего числа пустых окон и окон, содержащих единственный внутренний многоугольник. Такие окна сразу же изображаются. Провести проверку при помощи простого теста на пересечение для определения окон, пересекающих единственный многоугольник. Этот многоугольник отсекается и изображается. Провести проверку при помощи более сложных тестов для внешних и охватывающих многоугольников, чтобы определить дополнительные пустые окна и окна, охваченные единственным многоугольником. Такие окна сразу же изображаются. После реализации этих шагов проводится разбиение окна или делается попытка обнаружить такой охватывающий многоугольник, который был бы ближе к точке наблюдения, чем любой другой многоугольник. Если проводится разбиение, то решение последнего вопроса откладывается до достижения уровня пикселей. В любом случае требуется проводить тест глубины. Тест глубины проводится путем сравнения глубин (координат z) плоскостей, несущих многоугольники, в угловых точках окна. Если глубина охватывающего многоугольника больше, чем глубины всех остальных многоугольников в углах окна, то охватывающий многоугольник экранирует все остальные многоугольники в этом окне. Следовательно, данное окно можно визуализировать с тем значением интенсивности или цвета, которое соответствует охватывающему многоугольнику. Заметим, что приведенное условие по глубине является достаточным, но не необходимым для того, чтобы охватывающий многоугольник экранировал все остальные многоугольники в окне. В частности, если плоскость, несущая многоугольник, экранируется охватывающим многоугольником в углах окна, то сам многоугольник тоже экранируется последним в углах окна. Если же несущая плоскость не экранируется охватывающим окно многоугольником, то не очевидно, будет или нет экранирован многоугольник, лежащий в этой. Этот конфликт разрешается путем разбиения окна. Глубину несущей плоскости в углу окна можно вычислить с помощью ее уравнения. Например, если уравнение этой плоскости имеет вид: ax + by + cz + d = 0 а координаты угловой точки окна равны (xw, yw), то значение z = – (d + axw + byw)/c, c 0 равно искомой глубине. Всюду выше предполагалось, что все многоугольники следует сравнивать с каждым окном. Для сложных сцен это весьма неэффективно. Эффективность можно повысить, проведя сортировку по приоритету глубины (сортировку по z). Сортировка проводится по значению z координаты той вершины многоугольника, которая ближе других к точке наблюдения. В правой системе координат многоугольник с максимальным значением такой координаты z будет ближайшим к точке наблюдения. В списке отсортированных многоугольников он появится первым. При обработке каждого окна алгоритм ищет охватывающие его многоугольники. После обнаружения такого многоугольника запоминается величина z у его самой удаленной от наблюдателя вершины zsmin. При рассмотрении каждого очередного многоугольника в списке сравнивается координата z его ближайшей к наблюдателю вершины –zpmax с zsmin. Если zpmax < zsmin, то, очевидно, что очередной многоугольник экранируется охватывающим и не должен больше учитываться. Длину списка многоугольников, обрабатываемых для каждого окна, можно сократить, если воспользоваться информацией, полученной этим алгоритмом ранее. В частности, если многоугольник охватывает окно, то, очевидно, что он охватывает и все подокна этого окна и его можно больше не тестировать для них. Кроме того, если многоугольник является внешним по отношению к окну, то он будет внешним и для всех его подокон, и его можно не рассматривать при обработке этих подокон. Учитывать далее следует только пересекающие и внутренние многоугольники. Чтобы воспользоваться этой информацией, применяют три списка: для охватывающих, для внешних и для пересекающих и внутренних многоугольников. По ходу процесса разбиения многоугольники включаются в соответствующий список или удаляются из него. Запоминается также и уровень (шаг разбиения), на котором многоугольник впервые попадает в тот или иной список. Эта информация используется при обходе дерева, изображенного на рис. 2, в обратном порядке. На каждом шаге разбиения первым обрабатывается список охватывающих многоугольников для того, чтобы найти ближайший к наблюдателю многоугольник такого типа. Затем обрабатывается список пересекающих и внутренних многоугольников, чтобы проверить, не экранируются ли все они охватывающим многоугольником. Список внешних многоугольников игнорируется. Выше были изложены основные идеи и методы возможных улучшений алгоритма Варнока. Важно подчеркнуть, что нет единого алгоритма Варнока. Конкретные реализации этого алгоритма различаются в деталях. Если размер окна больше разрешающей способности дисплея и если оно еще содержит нечто, представляющее интерес, то алгоритм всегда будет разбивать окно. Чтобы идентифицировать внешние многоугольники для окон, размер которых больше размера пикселей, проводится простой габаритный тест с прямоугольной оболочкой. А для окон размером с пиксель выполняется более сложный тест, в котором видимый многоугольник определяется путем сравнения координат z всех многоугольников в центре пикселя. Однако здесь не используется сортировка по приоритету вдоль оси z, а также выигрыш, даваемый ранее накопленной информацией об относительном расположении многоугольников и окон. Алгоритм использует стек, максимальная длина которого равна: 3·(разрешение экрана в битах – 1) + 5. На рис. №4 приведена обобщенная блок-схема алгоритма Варнока.
5. Описание возможностей программы. Программа Varnok позволяет демонстрировать трёхмерные сцены из невыпуклых многогранников и производить их преобразования. Представлены следующие режимы изображения: Проволочный (рис. №5) Контурный (рис. №6) Полутоновый (рис. №7)  рис.4 “проволочный режим”  рис.4 “контурный режим”  рис.5 “полутоновый режим”
6. Интерфейс. 6.1. Главное окно. В главном окне демонстрируются 3D модели. Здесь же можно производить их преобразования(рис.6). 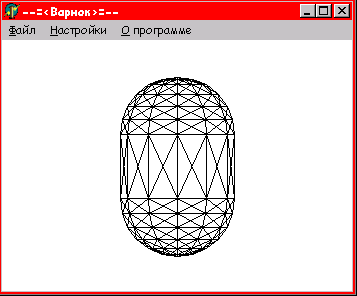 Рис.6
6.2 Меню Файл : Открыть – открывает новую модель созданную в 3D Studio Max (*.asc) или в другом 3D редакторе. Выход – закрывает программу
Настройки: Режим изображения – вид отображения модели(проволочный, контурный, полутоновый). Вращать – вращение модели вокруг осей X, Y и Z. Двигать – перемещение модели по сям X и Y. Масштабировать – увеличение и уменьшение модели. Сменить цвет фона – меняет цвет фона главного окна. Сменить цвет фигуры – меняет цвет фигуры.
7. Листинг Unit 1: procedure Line(p1,p2 : TPoint3d); //отрисовка линии procedure SetPoint(X, Y, Color: Longint); //установка точки procedure Line(p1,p2 : TPoint3d); begin Form1.PaintBox1.Canvas.Pen.Color := objcolor; Form1.PaintBox1.Canvas.MoveTo(p1^.x2d,p1^.y2d); Form1.PaintBox1.Canvas.LineTo(p2^.x2d,p2^.y2d); end;
procedure SetPoint(X, Y, Color: Longint); begin if ( (X>=0) and (X<SWidth) and (Y>=0) and (Y<SHeight) ) then Form1.PaintBox1.Canvas.Pixels[x,y] := Color; end;
procedure TForm1.FormCreate(Sender: TObject); begin foncolor:=RGB(255,255,255); //задаем исходно белый цвет фона objcolor:=RGB(0,0,0); //и черный - объекта ClearScreen(); //очищаем экран end;
procedure TForm1.ClearScreen(); begin Form1.PaintBox1.Canvas.Pen.Color := foncolor; Form1.PaintBox1.Canvas.Brush.Color:=foncolor; Form1.PaintBox1.Canvas.Brush.Style:=bsSolid; Form1.PaintBox1.Canvas.Rectangle(0,0,Width,Height); end;
procedure TForm1.PaintBox1Paint(Sender: TObject); begin SWidth := PaintBox1.Width; SHeight := PaintBox1.Height; MidX := Round(SWidth/2); MidY := Round(SHeight/2); ClearScreen(); if (Figure1<>nil) then Figure1.ShowFigure; //вызываем метод отрисовки фигуры end;
procedure TForm1.N2Click(Sender: TObject); begin //обработчик переключения на проволочный режим if (N2.Checked=false) then begin N3.Checked := false; N6.Checked := false; N2.Checked := true; Figure1.shading:=1; //устанавливаем флаг проволочного режима PaintBox1Paint(Sender); end; end;
procedure TForm1.N3Click(Sender: TObject); begin //обработчик переключения на контурный режим if (N3.Checked=false) then begin N2.Checked := false; N6.Checked := false; N3.Checked := true; Figure1.shading:=2; //устанавливаем флаг PaintBox1Paint(Sender); end; end;
procedure TForm1.Exit1Click(Sender: TObject); begin Close; end;
procedure TForm1.OpenAscFile1Click(Sender: TObject); var //процедура открытия ASCII файла s:string; ss:AnsiString; begin setlength(ss,1000); GetCurrentDirectory(1000,PChar(ss)); OpenDialog1.InitialDir:=ss; //начальный каталог при выборе файла - текущий if (OpenDialog1.Execute=true) then begin N2.Checked:=true; N3.Checked:=false; s:=OpenDialog1.FileName; if (Figure1<>nil) then Figure1.FigureDestroy; //уничтожаем старую копию фигуры если была Figure1 :=Figure.FigureCreate(s); //и создаем новую фигуру Options1.Enabled:=true; // включаем возможность регулировки настроек PaintBox1Paint(Sender); end; end;
Unit 2: procedure Normalize (V: TPoint3d); //приведение к единичному вектору var length: extended; begin length := sqrt((V^.x * V^.x) + (V^.y * V^.y) + (V^.z * V^.z));//общая длина V^.x := V^.x/length; V^.y := V^.y/length; V^.z := V^.z/length; end; //---------------------------------------------------------------------------
constructor Figure.FigureCreate(FileName: string); //конструктор класса begin //FileName - имя загружаемого файла numPoints := 0; // инициализация переменных numNormals := 0; numFaces := 0; LoadObject(FileName);//вызов метода "загрузка объекта" end;
destructor Figure.FigureDestroy; //удаление памяти связанной с классом var count: Longword; begin for count:=0 to (numPoints-1) do //все точки, грани, нормали dispose(points[count]); points := nil; //обнуляем сами массивы указателей for count:=0 to (numNormals-1) do dispose(normals[count]); normals := nil; for count:=0 to (numFaces-1) do dispose(polys[count]); polys := nil; end;
procedure Figure.SetMidPoint; //расчет координат точки центра объекта var count: Integer; tmpX,tmpY,tmpZ: extended; begin tmpX:=0; tmpY:=0; tmpZ:=0; for count:=0 to (numPoints-1) do begin tmpX := tmpX + points[count]^.x; //суммируем все координаты X Y Z tmpY := tmpY + points[count]^.y; tmpZ := tmpZ + points[count]^.z; end; tmpX := tmpX/numPoints; //и делим их на общее кол-во точек tmpY := tmpY/numPoints; tmpZ := tmpZ/numPoints;
midpoint.x := tmpX; //получаем точку центра объекта midpoint.y := tmpY; midpoint.z := tmpZ; end;
procedure Figure.CalcNormal(N: Longword); //расчет нормали (при загрузке) var //точки грани всегда заданы по часовой стрелке поэтому нормаль всегда выходит ИЗ объекта Vector1: array [0..2] of extended;//вспомогательные переменные Vector2: array [0..2] of extended; nx,ny,nz,l: extended; begin Vector1[0]:= polys[N]^.B^.x - polys[N]^.A^.x;// находим 2 вектора в плоскости Vector2[0]:= polys[N]^.C^.x - polys[N]^.A^.x;// грани Vector1[1]:= polys[N]^.B^.y - polys[N]^.A^.y; Vector2[1]:= polys[N]^.C^.y - polys[N]^.A^.y; Vector1[2]:= polys[N]^.B^.z - polys[N]^.A^.z; Vector2[2]:= polys[N]^.C^.z - polys[N]^.A^.z;
nx := Vector1[2]*Vector2[1] - Vector1[1]*Vector2[2];//находим векторное произведение ny := Vector1[0]*Vector2[2] - Vector1[2]*Vector2[0];//этих векторов nz := Vector1[1]*Vector2[0] - Vector1[0]*Vector2[1];//это и есть нормаль к грани
l:=sqrt((nx * nx) + (ny * ny) + (nz * nz));//нормализуем ее if (l<>0) then begin nx := nx/l; ny := ny/l; nz := nz/l; end;
new(normals[N]); //добавляем в список нормалей normals[N]^.x := nx; normals[N]^.y := ny; normals[N]^.z := nz; polys[N]^.normal := normals[N]; end;
procedure Figure.LoadObject(FileName: string); //метод "загрузка объекта" var f: Text; //открываемый текстовый файл str: string; Znach :string; Vertices, Faces: Longword; //общее кол-во вершин и граней count, A, B, C: Longword; X, Y, Z: extended; Code: Integer; n1,n2: byte; begin Assign(f,FileName); Reset(f);
while (not EOF(f)) do begin Readln(f,str);
if(Pos('Tri-mesh',str)<>0) then //ищем эту строку (она означает что сейчас begin // будет описание фигуры) n1:=21; n2:=Pos('Faces',str); //ищем положение этой строки n2:=n2-5; //n1 и n2 положения в строке числа Znach:=Copy(str,n1,n2-n1);//выделяем это число из строки Val(Znach,Vertices,Code);//преобразуем в числовой формат n1:=n2+5+7; n2:=Length(str)+1; Znach:=Copy(str,n1,n2-n1); Val(Znach,Faces,Code); numPoints := Vertices; numNormals := Faces; numFaces := Faces; SetLength(points,Vertices); //устанавливаем массивы указателей SetLength(normals,Faces); // в реальные значения SetLength(polys,Faces);
Readln(f,str); //пропускаем "Vertex list:" if (Pos('Mapped',str)<>0) then Readln(f,str);//текстурные коорд не нужны
for count:=0 to (Vertices-1) do begin Readln(f,str); n1:=Pos('X:',str)+2; n2:=Pos('Y:',str)-5; Znach:=Copy(str,n1,n2-n1); //выделяем координату Х Val(Znach,X,Code);
n1:=Pos('Y:',str)+2; n2:=Pos('Z:',str)-5; Znach:=Copy(str,n1,n2-n1); //выделяем координату У Val(Znach,Y,Code);
n1:=Pos('Z:',str)+2; if (Pos('U:',str)=0) then n2:=Length(str)+1 else n2:=Pos('U:',str)-5; Znach:=Copy(str,n1,n2-n1); //выделяем координату Z Val(Znach,Z,Code); new(points[count]); //выделяем память для точки points[count]^.x:=X; points[count]^.y:=Z; //в 3dMax обычно меняют Y c Z points[count]^.z:=Y; end;
Readln(f,str); //пропускаем "Face list:"
Readln(f,str);
for count:=0 to (Faces-1) do begin while Pos('Face',str)=0 do Readln(f,str); n1:=Pos('A:',str)+2; n2:=Pos('B:',str)-1; Znach:=Copy(str,n1,n2-n1);//выделяем позицию точки А Val(Znach,A,Code);
n1:=Pos('B:',str)+2; n2:=Pos('C:',str)-1; Znach:=Copy(str,n1,n2-n1);//выделяем позицию точки В Val(Znach,B,Code);
n1:=Pos('C:',str)+2; n2:=Pos('AB:',str)-1; Znach:=Copy(str,n1,n2-n1);//выделяем позицию точки С Val(Znach,C,Code); new(polys[count]); //выделяем память для грани polys[count]^.A:=points[A]; polys[count]^.B:=points[B]; polys[count]^.C:=points[C]; CalcNormal(count); //расчет нормали для этой грани Readln(f,str); end; shading:=1; //затенение - проволочное SetMidPoint; //расчет центра фигуры break; end; end; Close(f); //закрываем файл end; //Вращение относительно точки procedure Figure.RotateAboutPoint(X, Y, Z, angleX, angleY, angleZ: extended); var sinx,cosx,siny,cosy,sinz,cosz: extended; coordX,coordY,coordZ: extended; tX,tY,tZ: extended; count: Longword; begin sinx := Sin(angleX * PI / 180.0); //расчет синусов и косинусов углов поворота cosx := Cos(angleX * PI / 180.0); siny := Sin(angleY * PI / 180.0); cosy := Cos(angleY * PI / 180.0); sinz := Sin(angleZ * PI / 180.0); cosz := Cos(angleZ * PI / 180.0);
for count:=0 to (numPoints-1) do //вначале поворот всех точек begin coordX := points[count]^.x - X; //вычисляем локальные координаты coordY := points[count]^.y - Y; //(переносим в начало координат coordZ := points[count]^.z - Z;
tX := (coordX * cosz - coordY * sinz);//ось Z tY := (coordX * sinz + coordY * cosz); tZ := coordZ; coordY := (tY * cosx - tZ * sinx);//ось X coordZ := (tY * sinx + tZ * cosx); tZ := coordZ; coordX := (tZ * siny + tX * cosy);//ось Y coordZ := (tZ * cosy - tX * siny);
points[count]^.x := coordX + X;//преобразуем локальные координаты в мировые points[count]^.y := coordY + Y; points[count]^.z := coordZ + Z; end;
for count:=0 to (numNormals-1) do //затем поворот всех нормалей begin coordX := normals[count]^.x; coordY := normals[count]^.y; coordZ := normals[count]^.z;
tX := (coordX * cosz - coordY * sinz);//ось Z tY := (coordX * sinz + coordY * cosz); tZ := coordZ; coordY := (tY * cosx - tZ * sinx);//ось X coordZ := (tY * sinx + tZ * cosx); tZ := coordZ; coordX := (tZ * siny + tX * cosy);//ось Y coordZ := (tZ * cosy - tX * siny);
normals[count]^.x := coordX; normals[count]^.y := coordY; normals[count]^.z := coordZ; end; end; //вращать относительно начала координат procedure Figure.RotateWorldCoord(angleX, angleY, angleZ: extended); begin RotateAboutPoint(0,0,0,angleX,angleY,angleZ); end;
//перенос тела по осям procedure Figure.Translate(dX, dY, dZ: extended); var count: Longword; begin for count:=0 to (numPoints-1) do begin points[count]^.x:=points[count]^.x+dX; points[count]^.y:=points[count]^.y+dY; points[count]^.z:=points[count]^.z+dZ; end; end;
//масштабирование тела procedure Figure.Scale(sX, sY, sZ: extended); var count: Longword; coordX,coordY,coordZ: extended; begin for count:=0 to (numPoints-1) do begin coordX := points[count]^.x - midpoint.x; //переносим в начало координат coordY := points[count]^.y - midpoint.y; coordZ := points[count]^.z - midpoint.z;
coordX := coordX*sX; //масштабируем coordY := coordY*sY; coordZ := coordZ*sZ;
points[count]^.x := coordX + midpoint.x; //теперь обратно в мировые координаты points[count]^.y := coordY + midpoint.y; points[count]^.z := coordZ + midpoint.z; end; end;
//преобразование координат на плоскость (в экранные) procedure Figure.TransformToScreen; var count: Longword; begin for count:=0 to (numPoints-1) do begin points[count]^.x2d := Round(points[count]^.x) + MidX; //центруем по Х points[count]^.y2d := MidY - Round(points[count]^.y); //теперь по У end; //ось У идет вверх поэтому вычитаем end;
//метод отображающий фигуру procedure Figure.ShowFigure; begin
TransformToScreen(); case shading of 1: Wire; 2: Varnok; 3: Varnok; end; end;
procedure Figure.Wire; //рисует проволочный вид var count : Longword; begin for count:=0 to (numFaces-1) do begin Line(polys[count]^.A,polys[count]^.B); Line(polys[count]^.B,polys[count]^.C); Line(polys[count]^.C,polys[count]^.A); end; end; //////////////////////////////////////////////////////////////////////////////// // Набор структур и процедур для рисования методом Варнока
type //структура для занесения данных об обрабатываемом окне Window = record x,y,size:Longint; //координаты левой нижней точки и длина окна end;
var Stack: array of ^Window; //массив для занесения окон в стек Counter: Longword=0; //счетчик кол-ва окон в стеке
Xmin: array of Longint; //массивы координат прямоугольных оболочек граней Xmax: array of Longint; Ymin: array of Longint; Ymax: array of Longint; Colors: array of LongWord;
//процедура заталкивания окна в стек procedure Push(X,Y,SIZE: Longword); begin SetLength(Stack,Counter+1); //устанавливаем длину стека на 1-цу больше new(Stack[Counter]); //и добавляем следующее окно Stack[Counter]^.x:=X; Stack[Counter]^.y:=Y; Stack[Counter]^.size:=SIZE; inc(Counter); end;
//процедура извлечения окна из стека procedure Pop(var X: Longint;var Y: Longint;var SIZE: Longint); begin if (Counter-1)<0 then exit; X:=Stack[Counter-1]^.x; Y:=Stack[Counter-1]^.y; SIZE:=Stack[Counter-1]^.size; dispose(Stack[Counter-1]); SetLength(Stack,Counter-1); //уменьшаем стек на 1-цу dec(Counter); end;
//тест прямоугольных оболочек граней на попадание в окно function simple_triangle_Test(N,X,Y,SIZE: Longint):boolean; var Xleft,Xright,Ybottom,Ytop: Longint; begin
Xleft := X; Xright := X+SIZE-1; Ytop := Y; Ybottom := Y+SIZE-1;
if (Xmin[N]>Xright) then begin simple_triangle_Test:=false; exit; end; if (Xmax[N]<Xleft) then begin simple_triangle_Test:=false; exit; end; if (Ymax[N]<Ytop) then begin simple_triangle_Test:=false; exit; end; if (Ymin[N]>Ybottom) then begin simple_triangle_Test:=false; exit; end;
simple_triangle_Test:=true; //если пересекает окно значит true end;
//фунция расчета глубины по Z треугольника в точке экрана (Х,У) function ZDepth(X,Y:Longword; tP:TTriangle):extended; type fpoint = record x,y,z: extended; end; var PX,PY:extended; p,q: fpoint; //векторы в грани n: fpoint; //нормаль к грани cc: extended; //свободный член ур-ния плоскости A,B,C: TPoint3d; begin //ур-ние n.x*x+n.y*y+n.z*z-cc=0 Zdepth:=100000000; A := tP^.A; B := tP^.B; C := tP^.C;
p.x := B^.x2d-A^.x2d;//1-й вектор в грани p.y := B^.y2d-A^.y2d; p.z := B^.z-A^.z; q.x := C^.x2d-A^.x2d;//2-й вектор q.y := C^.y2d-A^.y2d; q.z := C^.z-A^.z;
n.z := p.x*q.y-p.y*q.x; //их векторное произведение n.x := p.y*q.z-p.z*q.y; n.y := -(p.x*q.z-p.z*q.x);
cc := n.x*A^.x2d+n.y*A^.y2d+n.z*A^.z; //свободный член
PX:=X+0.5; //расчет в середине пикселя PY:=Y+0.5;
if n.z<>0 then Zdepth := (cc - n.x*PX - n.y*PY)/n.z; //возвращает координату Z в этой точке end;
// точная проверка того охватывает ли хотя бы одна грань окно размером с пиксел // и координатами X,Y для контурного режима function in_Window(X,Y: Longword; P: array of TTriangle; N:Longword):Longint; var Zmin: extended; //минимальное Z в этом окне (ближе всех к наблюдателю) Z: extended; A,B,C: TPoint3d; //временные точки AB,BC,CA,AD,BD,CD: Point3d; D: Point3d; f1,f2,f3: extended; s1,s2,s3,s4: extended; i:Longint;
begin in_Window:=-1; Zmin:= 10000000; //заполняем Z максимальным значением т.е. как самый отдаленный for i:=0 to (N-1) do //цикл проверки по всем граням begin A := P[i]^.A; B := P[i]^.B; C := P[i]^.C;
if ((A^.y2d = B^.y2d)and(A^.y2d = C^.y2d)) then continue; //если грань видна как линия if ((A^.x2d = B^.x2d)and(A^.x2d = C^.x2d)) then continue; //то пропускаем ее
D.x := X; //заносим координаты левой верхней координаты пикселя D.y := Y;
AB.x := B^.x2d - A^.x2d; //рассчитываем векторы сторон грани AB.y := B^.y2d - A^.y2d; BC.x := C^.x2d - B^.x2d; BC.y := C^.y2d - B^.y2d; CA.x := A^.x2d - C^.x2d; CA.y := A^.y2d - C^.y2d;
AD.x := D.x - A^.x2d; //рассчит. векторы от вершин грани до верхней координаты пикселя AD.y := D.y - A^.y2d; BD.x := D.x - B^.x2d; BD.y := D.y - B^.y2d; CD.x := D.x - C^.x2d; CD.y := D.y - C^.y2d;
f1 := AB.x*AD.y - AD.x*AB.y; //находим векторные произведения векторов сторон грани f2 := BC.x*BD.y - BD.x*BC.y; //с предыдущими рассчитанными векторами f3 := CA.x*CD.y - CD.x*CA.y; if ( (f1<0)and(f2<0)and(f3<0) ) then s1 := -1 else s1 := 1;//если все 3 значения f1,f2,f3 if ((f1=0)and(f2<=0)and(f3<=0)) then s1 := 0; //отрицательны то точка внутри грани if ((f2=0)and(f1<=0)and(f3<=0)) then s1 := 0; //если одно значение=0 а другие <=0 то if ((f3=0)and(f1<=0)and(f2<=0)) then s1 := 0; //точка находится на самой грани //иначе она вне грани //s1<0 если точка вне грани s1>0 если внутри, и s1=0 если на стороне грани
//далее вычисляем флаги для верхней правой координаты пикселя //абсолютно также D.x := X+1; D.y := Y;
AD.x := D.x - A^.x2d; AD.y := D.y - A^.y2d; BD.x := D.x - B^.x2d; BD.y := D.y - B^.y2d; CD.x := D.x - C^.x2d; CD.y := D.y - C^.y2d;
f1 := AB.x*AD.y - AD.x*AB.y; f2 := BC.x*BD.y - BD.x*BC.y; f3 := CA.x*CD.y - CD.x*CA.y; if ( (f1<0)and(f2<0)and(f3<0) ) then s2 := -1 else s2 := 1; if ((f1=0)and(f2<=0)and(f3<=0)) then s2 := 0; if ((f2=0)and(f1<=0)and(f3<=0)) then s2 := 0; if ((f3=0)and(f1<=0)and(f2<=0)) then s2 := 0;
//вычисляем флаги для нижней левой координаты пикселя //абсолютно также D.x := X; D.y := Y+1;
AD.x := D.x - A^.x2d; AD.y := D.y - A^.y2d; BD.x := D.x - B^.x2d; BD.y := D.y - B^.y2d; CD.x := D.x - C^.x2d; CD.y := D.y - C^.y2d;
f1 := AB.x*AD.y - AD.x*AB.y; f2 := BC.x*BD.y - BD.x*BC.y; f3 := CA.x*CD.y - CD.x*CA.y; if ( (f1<0)and(f2<0)and(f3<0) ) then s3 := -1 else s3 := 1; if ((f1=0)and(f2<=0)and(f3<=0)) then s3 := 0; if ((f2=0)and(f1<=0)and(f3<=0)) then s3 := 0; if ((f3=0)and(f1<=0)and(f2<=0)) then s3 := 0;
//вычисляем флаги для нижней правой координаты пикселя //абсолютно также D.x := X+1; D.y := Y+1;
AD.x := D.x - A^.x2d; AD.y := D.y - A^.y2d; BD.x := D.x - B^.x2d; BD.y := D.y - B^.y2d; CD.x := D.x - C^.x2d; CD.y := D.y - C^.y2d;
f1 := AB.x*AD.y - AD.x*AB.y; f2 := BC.x*BD.y - BD.x*BC.y; f3 := CA.x*CD.y - CD.x*CA.y; if ( (f1<0)and(f2<0)and(f3<0) ) then s4 := -1 else s4 := 1; if ((f1=0)and(f2<=0)and(f3<=0)) then s4 := 0; if ((f2=0)and(f1<=0)and(f3<=0)) then s4 := 0; if ((f3=0)and(f1<=0)and(f2<=0)) then s4 := 0;
//теперь если все вершины пикселя внутри грани то заполняем фоновым цветом if ( (s1<0)and(s2<0)and(s3<0)and(s4<0) ) then begin Z := ZDepth(X,Y,P[i]); if (Z<Zmin) then //если коорд. Z текущей грани меньше (грань ближе к наблюдателю) begin //то рисуем пиксель Zmin := Z; in_window := foncolor; end; continue; end else //если левые верхняя и нижняя вершины пикселя или верхние левая и правая -||- лежат на стороне грани if ( ((s1=0)and(s3=0))or((s1=0)and(s2=0)) ) then //то закрашиваем цветом фигуры begin Z := ZDepth(X,Y,P[i]); if (Z<Zmin) then begin Zmin := Z; in_window := objcolor; end; continue; end //если правые верхняя и нижняя вершины пикселя или нижние левая и правая -||- лежат на стороне грани else //то пропускаем if ( ((s2=0)and(s4=0))or((s3=0)and(s4=0)) ) then else //если вершины пикселя лежат по по разные стороны от стороны грани то рисуем цветом фигуры if ( not((s1>=0)and(s2>=0)and(s3>=0)and(s4>=0)) ) then begin Z := ZDepth(X,Y,P[i]); if (Z<Zmin) then begin Zmin := Z; in_window := objcolor; end; continue; end; end; end;
// точная проверка того охватывает ли хотя бы одна грань окно размером с пиксел // и координатами X,Y для полутонового режима function in_WindowPainted(X,Y: Longword; P: array of TTriangle; N:Longword):Longint; var Zmin: Real; //минимальное Z в этом окне (ближе всех к наблюдателю) AB,BC,CA: Point3d; AD,BD,CD: Point3d; A,B,C: TPoint3d; Z: Real; f1,f2,f3: Real; i:Longword; begin in_WindowPainted:=-1; Zmin:= 10000000; //заполняем Z максимальным значением т.е. как самый отдаленный for i:=0 to (N-1) do //цикл проверки по всем граням begin A := P[i]^.A; B := P[i]^.B; C := P[i]^.C;
if ((A^.y2d = B^.y2d)and(A^.y2d = C^.y2d)) then continue; //если грань видна как линия if ((A^.x2d = B^.x2d)and(A^.x2d = C^.x2d)) then continue; //то пропускаем ее
AB.x := B^.x2d-A^.x2d;//рассчитываем векторы сторон грани AB.y := B^.y2d-A^.y2d; BC.x := C^.x2d-B^.x2d; BC.y := C^.y2d-B^.y2d; CA.x := A^.x2d-C^.x2d; CA.y := A^.y2d-C^.y2d;
AD.x := X+0.5 - A^.x2d; //рассчит. векторы от вершин грани до окна размером в пиксель AD.y := Y+0.5 - A^.y2d; //причем в середине этого окна BD.x := X+0.5 - B^.x2d; //для расчета принадлежности этого окна полигону BD.y := Y+0.5 - B^.y2d; CD.x := X+0.5 - C^.x2d; CD.y := Y+0.5 - C^.y2d;
f1 := AB.x*AD.y - AD.x*AB.y; //находим векторные произведения векторов сторон грани f2 := BC.x*BD.y - BD.x*BC.y; //с предыдущими рассчитанными векторами f3 := CA.x*CD.y - CD.x*CA.y; //если получились отрицательные числа для каждой стороны //то окно внутри полигона //если хотя бы одно равно 0 то окно находится на стороне if ((f1<=0)and(f2<=0)and(f3<=0)) then begin Z := ZDepth(X,Y,P[i]); //ищем коорд. Z для этой точки if (Z<Zmin) then //если ближе begin Zmin := Z; in_WindowPainted := Colors[i]; end; continue; end; end; end;
procedure Figure.Varnok; var x,y,size:Longint; flag: boolean; V1: TPoint3d; V2: Point3d; ugol, tmp: extended; num,count : Longint; //счетчики polylst: array of TTriangle; //массив обрабатываемых граней A,B,C:TPoint3d; color: Longint; LightPosition: Point3d; Hue, Luminance, Saturation: Word;//для преобразования цвета из RGB в систему HLS
begin V2.x:=0; //вектор направления взгляда V2.y:=0; V2.z:=-1; num:=0; for count:=0 to (numFaces-1) do begin V1 := polys[count]^.normal; ugol:= V1^.x*V2.x + V1^.y*V2.y + V1^.z*V2.z; //проверяем совпадает ли направление взгляда if (ugol>0) then //с нормалью. Если грань не видна то ugol будет меньше или равен нулю begin inc(num); SetLength(polylst,num); polylst[num-1] := polys[count];//видимые грани добавляем в список обрабатываемых end; end; SetLength(Xmin,num); //расчитываем прямоугольные оболочки граней SetLength(Xmax,num); SetLength(Ymin,num); SetLength(Ymax,num); for count:=0 to (num-1) do begin A:=polylst[count]^.A; B:=polylst[count]^.B; C:=polylst[count]^.C; if (A^.x2d<B^.x2d) then Xmin[count] := A^.x2d else Xmin[count] := B^.x2d; if (Xmin[count]>C^.x2d) then Xmin[count] := C^.x2d;
if (A^.x2d>B^.x2d) then Xmax[count] := A^.x2d else Xmax[count] := B^.x2d; if (Xmax[count]<C^.x2d) then Xmax[count] := C^.x2d;
if (A^.y2d<B^.y2d) then Ymin[count] := A^.y2d else Ymin[count] := B^.y2d; if (Ymin[count]>C^.y2d) then Ymin[count] := C^.y2d;
if (A^.y2d>B^.y2d) then Ymax[count] := A^.y2d else Ymax[count] := B^.y2d; if (Ymax[count]<C^.y2d) then Ymax[count] := C^.y2d; end;
if (shading=3) then begin LightPosition.x:=0; LightPosition.y:=0; LightPosition.z:=-1000000; SetLength(Colors, num); for count:=0 to (num-1) do begin //находим вектор между источником света и любой точкой из грани V2.x := LightPosition.x - polylst[count]^.A^.x; V2.y := LightPosition.y - polylst[count]^.A^.x; V2.z := LightPosition.z - polylst[count]^.A^.x; tmp:=sqrt(V2.x*V2.x+V2.y*V2.y+V2.z*V2.z);//находим длину вектора V2.x:=V2.x/tmp; //нормализуем вектор (приводим к единичной длине) V2.y:=V2.y/tmp; V2.z:=V2.z/tmp; //расчет коэффициента яркости //1 - макс. яркость, 0 - миним. tmp := polylst[count]^.normal^.x*V2.x+polylst[count]^.normal^.y*V2.y + polylst[count]^.normal^.z*V2.z; if (tmp<0) then tmp:=0; if (tmp>1) then tmp:=1; ColorRGBToHLS(objcolor,Hue, Luminance, Saturation); Colors[count] := ColorAdjustLuma(objcolor,round(Luminance*tmp)-Luminance,true); end; end;
Push(0,0,1024); //заносим 1-е окно в стек //причем длиной 1024 т.е. размер экрана не должен превышать 1024x1024 while (Counter>0) do //цикл работает пока есть хотя бы 1но окно в стеке begin Pop(x,y,size); //извлекаем окно из стека flag:=false; //флаг пересечения грани с окном for count:=0 to (num-1) do //цикл проверки всех прямоуг. оболочек граней на пересечение с окном if (simple_triangle_Test(count,x,y,size)) then begin flag:=true; //если пересекает хотя бы одна грань то устанавливаем флаг break; end;
if (flag) then begin if (size>1) then //если окно больше пикселя то разбиваем его еще на 4 begin size := size div 2; Push(x+size,y+size,size); Push(x,y+size,size); Push(x+size,y,size); Push(x,y,size); end //if size else //если грань пересекает окно размером с пиксел то рассчитываем цвет этой точки begin if (shading=3) then color:=in_WindowPainted(x,y,polylst,num) //если полутоновый else color:=in_Window(x,y,polylst,num); //если контурный if (color>=0) then begin SetPoint(x,y,color);//устанавливаем рассчитанный цвет пикселя end; end; end; end; SetLength(polylst,0); //удаляем временные списки SetLength(Xmin,0); SetLength(Xmax,0); SetLength(Ymin,0); SetLength(Ymax,0); if (shading=3) then SetLength(Colors,0); end.
Unit 3: procedure TOKBottomDlg.Button1Click(Sender: TObject); begin case RadioButton1.Checked of //если включен режим true: //вращать "относительно начала координат" begin Figure1.RotateWorldCoord(5,0,0); Form1.PaintBox1Paint(Sender); end; false: begin Figure1.RotateAboutPoint(Figure1.midpoint.x,Figure1.midpoint.y,Figure1.midpoint.z,5,0,0); Form1.PaintBox1Paint(Sender); end; end; end;
procedure TOKBottomDlg.Button2Click(Sender: TObject); begin case RadioButton1.Checked of true: begin Figure1.RotateWorldCoord(-5,0,0); Form1.PaintBox1Paint(Sender); end; false: begin Figure1.RotateAboutPoint(Figure1.midpoint.x,Figure1.midpoint.y,Figure1.midpoint.z,-5,0,0); Form1.PaintBox1Paint(Sender); end; end; end;
procedure TOKBottomDlg.Button3Click(Sender: TObject); begin case RadioButton1.Checked of true: begin Figure1.RotateWorldCoord(0,5,0); Form1.PaintBox1Paint(Sender); end; false: begin Figure1.RotateAboutPoint(Figure1.midpoint.x,Figure1.midpoint.y,Figure1.midpoint.z,0,5,0); Form1.PaintBox1Paint(Sender); end; end; end;
procedure TOKBottomDlg.Button4Click(Sender: TObject); begin case RadioButton1.Checked of true: begin Figure1.RotateWorldCoord(0,-5,0); Form1.PaintBox1Paint(Sender); end; false: begin Figure1.RotateAboutPoint(Figure1.midpoint.x,Figure1.midpoint.y,Figure1.midpoint.z,0,-5,0); Form1.PaintBox1Paint(Sender); end; end; end;
procedure TOKBottomDlg.Button5Click(Sender: TObject); begin case RadioButton1.Checked of true: begin Figure1.RotateWorldCoord(0,0,5); Form1.PaintBox1Paint(Sender); end; false: begin Figure1.RotateAboutPoint(Figure1.midpoint.x,Figure1.midpoint.y,Figure1.midpoint.z,0,0,5); Form1.PaintBox1Paint(Sender); end; end; end;
procedure TOKBottomDlg.Button6Click(Sender: TObject); begin case RadioButton1.Checked of true: begin Figure1.RotateWorldCoord(0,0,-5); Form1.PaintBox1Paint(Sender); end; false: begin Figure1.RotateAboutPoint(Figure1.midpoint.x,Figure1.midpoint.y,Figure1.midpoint.z,0,0,-5); Form1.PaintBox1Paint(Sender); end; end; end; end.
Unit 4: procedure TForm4.Button2Click(Sender: TObject); begin Figure1.Translate(5,0,0); //вызов метода для перемещения Form1.PaintBox1Paint(Sender); end;
procedure TForm4.Button3Click(Sender: TObject); begin Figure1.Translate(-5,0,0); Form1.PaintBox1Paint(Sender); end;
procedure TForm4.Button4Click(Sender: TObject); begin Figure1.Translate(0,5,0); Form1.PaintBox1Paint(Sender); end;
procedure TForm4.Button5Click(Sender: TObject); begin Figure1.Translate(0,-5,0); Form1.PaintBox1Paint(Sender); end; end.
Unit 5: procedure TForm5.Button2Click(Sender: TObject); begin Figure1.Scale( 1.1,1.1,1.1); //вызов метода для масштабирования Form1.PaintBox1Paint(Sender); end;
procedure TForm5.Button3Click(Sender: TObject); begin Figure1.Scale( 0.9,0.9,0.9); //вызов метода для масштабирования Form1.PaintBox1Paint(Sender); end; end.
11. Список литературы. Материалы сайта: www.rusdoc.ru. Материалы сайта: www.kursk.ru. Материалы сайта: www.citos.ru. Тимофей Самарский “Увлекательный мир программирования” М: Бином, 1996., Павлидис Т. Алгоритмы машинной графики и обработки изображений. Пер. с англ. М.: Радио и связь, 1986. Архангельский А.Г. “Delphi 6” Спб:Питер, 2001
Набайоти Баркакати “Программирование игр для Windows на Borland C++ ” М: Бином, 1994., стр. 284-286. Для написания данного пункта использовались материалы сайта: www.kursk.ru. 60
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ. ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ.
Кафедра Информационных систем и технологий. Дисциплина – Системная организация САПР.
П  одписано к защите Принято одписано к защите Принято З  ащита состоится Оценка ащита состоится Оценка  Подпись членов коммиссии Подпись членов коммиссии Р  уководитель уководитель  

Расчетно – пояснительная записка к курсовому проекту.
Тема: Удаление невидимых линий и поверхностей с помощью алгоритма Варнока.
КП 071900.18
Исполнитель: Белов Артём Борисович Группа: ИТ-41 |