Министерство образования Российской Федерации
Дальневосточный государственный университет
Специальность:
"Менеджмент организаций"
Контрольная работа
По предмету: "Статистика"
Владивосток 2007
1. Результаты сессии приведены в таблице:
| Балл оценки
|
2 (неуд.)
|
3 (удовл.)
|
4 (хорошо)
|
5 (отлично)
|
Всего
|
| Число студентов
|
5
|
45
|
110
|
40
|
200
|
Рассчитайте:
1. Средний балл успеваемости.
2. Показатели вариации уровня знаний.
3. Структуру численности студентов по успеваемости.
Сделайте выводы
Решение
Найдем средний балл успеваемости за сессию используя следующую формулу:
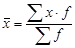 или или 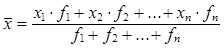
где x – индивидуальное значение усредняемого признака – балл оценки,
f – численность единиц совокупности – число студентов.
Подставив значения x и f по данным таблицы: x1
=2, x2
=3, x3
=4, x4
=5;
f1
=5, f2
=45, f3
=110, f4
=40, получаем уравнение:
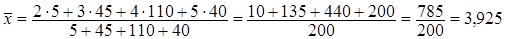
Средний балл успеваемости за сессию составляет 3,93.
Коэффициент вариации вычисляем по формуле:
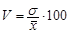
Для определения дисперсии (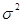 ) найдем отклонения от среднего по каждому усредняемому признаку x, возведем их в квадрат и просуммируем. Общая сумма квадратов отклонений: ) найдем отклонения от среднего по каждому усредняемому признаку x, возведем их в квадрат и просуммируем. Общая сумма квадратов отклонений:
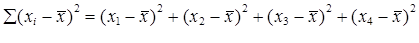
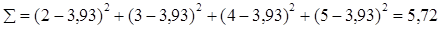
Дисперсия (средний квадрат отклонений) составит:
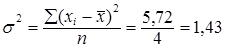
Зная дисперсию найдем среднее квадратическое отклонение
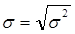
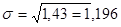
Коэффициент вариации 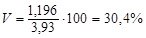
Следовательно, в среднем вариация уровня знаний составляет 1,196 балла или 30,4%
Относительная величина структуры рассчитывается как процентное отношение части целого к целому:
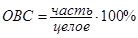
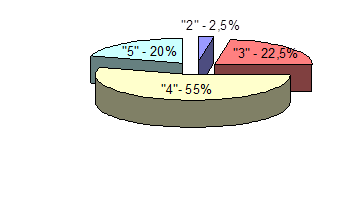
Если общая численность студентов сдававших сессию – 200, то в процентном выражении количество получивших оценку 2 составляет 2,5%, 3 – 22,5%, 4 – 55%, 5 – 20%.
То есть число студентов, сдавших сессию успешно составляет 3 / 4 (75%) от общей численности, а количество получивших «неуд.» и, следовательно, не сдавших сессию составляет 1/40 от общей численности.
Структура численности студентов по успеваемости выглядит следующим образом:
Задача 2. Построить интервальный ряд распределения малых предприятий Приморского края по размеру капитальных вложений.
Имеются данные (табл. 1.9.) об основных показателях финансово-хозяйственной деятельности малых предприятий в 1996 году по Приморскому краю.
Таблица 1.9.
| |
Основные показатели финансово-хозяйственной деятельности малых предприятий в 1996 г. 1
|
| |
Количество предприятий, ед.
|
Среднесписочная численность, чел.
|
Среднемесячная заработная плата, руб.
|
Объем произведенной продукции на 1 работающ., тыс. руб.
Реклама

|
Балансовая прибыль (+) или убытки (–), млн. руб.
|
Капитальные вложения, тыс. руб.
|
| 1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
| ВСЕГО по краю, в том числе по районам
|
11372
|
109535
|
624
|
71,5
|
-56144
|
172093
|
| Арсеньев
|
193
|
2113
|
678
|
50,7
|
-345
|
850
|
| Артем
|
475
|
4539
|
561
|
39,7
|
14357
|
409
|
| Большой Камень
|
145
|
1324
|
599
|
46,5
|
677
|
284
|
| Владивосток
|
6788
|
55584
|
627
|
99,8
|
-534568
|
142232
|
| Дальнегорск
|
146
|
1835
|
504
|
35,5
|
-13007
|
90
|
| Дальнереченск
|
82
|
1003
|
678
|
36,6
|
-4
|
115
|
| Лесозаводск
|
66
|
824
|
736
|
35,7
|
-2337
|
194
|
| Находка
|
1339
|
14117
|
792
|
60,6
|
-17672
|
7562
|
| Партизанск
|
201
|
2449
|
552
|
29,8
|
-11560
|
602
|
| Спасск-Дальний
|
74
|
1829
|
693
|
39,5
|
-6505
|
273
|
| Уссурийск
|
716
|
7741
|
564
|
47
|
10505
|
4797
|
| Фокино
|
77
|
765
|
235
|
35,8
|
1860
|
57
|
| Анучинский
|
32
|
506
|
456
|
10
|
-729
|
626
|
| Дальнегорский
|
5
|
13
|
506
|
3
|
5
|
114
|
| Дальнереченский
|
11
|
237
|
278
|
8,6
|
-1501
|
-
|
| Кавалеровский
|
66
|
1533
|
477
|
14,5
|
-2271
|
799
|
| Кировский
|
18
|
615
|
633
|
10,1
|
232
|
37
|
| Красноармейский
|
35
|
642
|
707
|
25,6
|
5761
|
625
|
| Лазовский
|
35
|
512
|
785
|
20,1
|
929
|
1353
|
| Лесозаводский
|
5
|
92
|
237
|
2
|
-721
|
105
|
| Михайловский
|
93
|
959
|
503
|
46,8
|
-3143
|
789
|
| Надеждинский
|
74
|
957
|
710
|
52,3
|
6049
|
586
|
| Октябрьский
|
130
|
1098
|
344
|
31,5
|
147
|
149
|
| Ольгинский
|
24
|
349
|
388
|
29,4
|
1377
|
1
|
| Партизанский
|
85
|
1317
|
516
|
38,1
|
595
|
6622
|
| Пограничный
|
35
|
330
|
622
|
29,5
|
502
|
295
|
Решение
1. Для построения интервального ряда определим число групп по формуле Стерджесса:
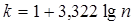 , ,
где n – число единиц изучаемой совокупности, т.е. число районов – 26.
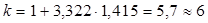 интервалов (групп) интервалов (групп)
2. Вычислим величину интервала: 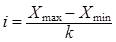
Исходя из данных таблицы – X
max
=142232 тыс. руб. (г. Владивосток), X
min
=0 (Дальнереченский р-он), следовательно 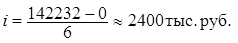
3. Представляем интервальный ряд распределения малых предприятий по размеру капитальных вложений с интервалом 2400 тыс. руб. в таблице:
| № группы п/п
|
Группы по размеру капитальных вложений,
тыс. руб.
|
Количество территор. единиц совокупности в группе, наименования
|
Количество
предприятий
в
группе
|
Сумма капитальных вложений в группе, тыс
|
Доля в % к общему размеру капитальных вложений по краю
|
| 1.
|
До 2400
|
14
|
Дальнереченский
|
1354
|
2123
|
1,2
|
| |
|
|
Ольгинский
|
|
|
|
| |
|
|
Кировский
|
|
|
|
| |
|
|
Фокино
|
|
|
|
| |
|
|
Дальнегорск
|
|
|
|
| |
|
|
Лесозаводский
|
|
|
|
| |
|
|
Дальнегорский
|
|
|
|
| |
|
|
Дальнереченск
|
|
|
|
| |
|
|
Октябрьский
|
|
|
|
| |
|
|
Лесозаводск
|
|
|
|
| |
|
|
Спасск-Дальний
|
|
|
|
| |
|
|
Большой Камень
|
|
|
|
| |
|
|
Пограничный
|
|
|
|
| |
|
|
Артем
|
|
|
|
| 2.
|
2400–4800
|
6
|
Надеждинский
|
501
|
4027
|
2,3
|
| |
|
|
Партизанск
|
|
|
|
| |
|
|
Красноармейский
|
|
|
|
| |
|
|
Анучинский
|
|
|
|
| |
|
|
Михайловский
|
|
|
|
| |
|
|
Кавалеровский
|
|
|
|
| 3.
|
4800–7200
|
3
|
Арсеньев
|
944
|
7000
|
4,1
|
| |
|
|
Лазовский
|
|
|
|
| |
|
|
Уссурийск
|
|
|
|
| 4.
|
7200–9600
|
1
|
Находка
|
1339
|
7562
|
4,4
|
| 5.
|
9600–12000
|
-
|
|
-
|
-
|
|
| 6.
|
12000 и более
|
2
|
Партизанский
|
6873
|
148854
|
87
|
| |
|
|
Владивосток
|
|
|
|
Из таблицы видно неравномерное распределение объема капитальных вложений, более 80% которых приходится на малые предприятия г. Владивостока.
Задача 3. По данным таблицы №№КБ с 6 по 30 требуется:
1) рассчитать показатели, характеризующие связь между размером прибыли, величиной неликвидных активов (
х1
) и размером ссуд (
х2
);
Реклама

2) дать оценку выборочных коэффициентов корреляции
ryx1
3) по расчетам сделать выводы и принять решение.
| №№ п/п
|
Наименование банка
|
Прибыль
|
Ссуды
|
Неликвидные активы
|
Привлеченные средства, тыс. руб.
|
|
|
|
x4
|
x2
|
x1
|
x3
|
| 1.
|
Большой камень банк
|
1212
|
14595
|
110
|
15327
|
| 2.
|
Восток бизнесбанк
|
7677
|
37299
|
5592
|
72860
|
| 3.
|
Дальневосточный банк
|
25555
|
518850
|
1800178
|
892145
|
| 4.
|
Дальрыббанк
|
-104191
|
134510
|
165014
|
450832
|
| 5.
|
Банк «Меркурий»
|
374
|
9164
|
2218
|
13554
|
| 6.
|
Банк «Приморье»
|
14599
|
385862
|
78077
|
604834
|
| 7.
|
Примсоцбанк
|
1837
|
166423
|
19885
|
232007
|
| 8.
|
Примтеркомбанк
|
1230
|
13659
|
966
|
12514
|
| 9.
|
Далькомбанк
|
103358
|
656262
|
49341
|
1381192
|
| 10.
|
Банк «Дземки»
|
8047
|
73345
|
8875
|
100358
|
| 11.
|
Банк «Конэкагропром»
|
-849
|
131758
|
8349
|
152694
|
| 12.
|
Регионбанк
|
7567
|
317375
|
43232
|
482305
|
| 13.
|
Банк «Уссури»
|
2148
|
16260
|
3
|
14731
|
| 14.
|
Амурбанк
|
-8694
|
7930
|
2249
|
11368
|
| 15.
|
Белогорскагрокомбанк
|
1435
|
11212
|
1
|
12357
|
| 16.
|
Супербанк
|
653
|
16386
|
142
|
25448
|
| 17.
|
Камчатбизнесбанк
|
1094
|
6867
|
1295
|
40059
|
| 18.
|
Банк «Камчатка»
|
1382
|
12046
|
1801
|
27026
|
| 19.
|
Камчаткомагропромбанк
|
46192
|
320153
|
43305
|
676113
|
| 20.
|
Камчатпромбанк
|
9988
|
66912
|
19299
|
231853
|
| 21.
|
Камчатпрофитбанк
|
19446
|
88076
|
6862
|
258057
|
| 22.
|
Камчатрыббанк
|
1052
|
17815
|
2038
|
33347
|
| 23.
|
«ПИКОбанк»
|
5625
|
19062
|
4885
|
21201
|
| 24.
|
Банк «ИТУРУП»
|
9733
|
39217
|
418
|
285888
|
| 25.
|
Банк «Сахалин-Вест»
|
6193
|
31622
|
1513
|
118615
|
| 26.
|
Банк «Холмск»
|
-929
|
13571
|
612
|
24434
|
| 27.
|
«Колыма-БАНК»
|
6044
|
84157
|
35173
|
143994
|
| 28.
|
Банк «Магаданский»
|
548
|
25280
|
331
|
33650
|
| 29.
|
Алданзолотобанк
|
807
|
6212
|
3149
|
28848
|
| 30.
|
Алмазэргиенбанк
|
13695
|
59600
|
5493
|
173437
|
| 31.
|
Банк «Майинский»
|
647
|
3697
|
187
|
1655
|
| 32.
|
Нерюнгрибанк
|
6269
|
33965
|
5586
|
116584
|
Решение
1. Исх. данные:
| Вид товара
|
БАЗИСНЫЙ ПЕРИОД («0»)
|
ОТЧЕТНЫЙ ПЕРИОД («1»)
|
| Цена за 1 кг, тыс. руб.
|
Продано, тонн
|
Цена за 1 кг, тыс. руб.
|
Продано, тонн
|
| 1
|
2
|
3
|
4
|
5
|
| А
|
4,50
|
500
|
4,90
|
530
|
| Б
|
2,00
|
200
|
2,10
|
195
|
| В
|
1,08
|
20
|
1,00
|
110
|
Решение
Индекс – это показатель сравнения двух состояний одного и того же явления (простого или сложного, состоящего из соизмеримых или несоизмеримых элементов); включает 2 вида:
- Отчетные, оцениваемые данные («1»)
- Базисные, используемые в качестве базы сравнения («0»)
1) Найдем индивидуальные индексы по формулам:
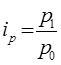 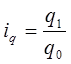
(где: р, q – цена, объем соответственно; р1
, р0
- цена отчетного, базисного периодов соответственно; q1
, q2
– объем отчетного, базисного периодов соответственно)
· для величины 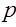 (цены) по каждому виду товара (цены) по каждому виду товара
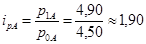
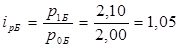
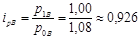
· для величины q (объема) по каждому виду товаров:
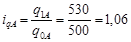
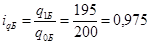
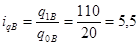
2) Найдем общие индексы по формулам:
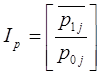 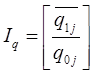 
представляет собой среднее значение индивидуальных индексов (цены, объема), где j – номер товара.
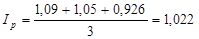
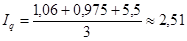
3) Общий индекс товарооборота равен: 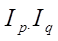
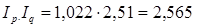
4) Найдем абсолютное изменение показателя (экономии или перерасхода):
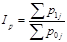
получаем: 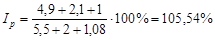
Вывод:
наблюдается перерасход денежных средств населения в результате изменения цен на товары в отчетном периоде по сравнению с базисным, в среднем на 5,54%.
2. Коэффициент корреляции оценивает тесноту связи между несколькими признаками. В данном случае требуется оценить связь между двумя признаками. Поэтому необходимо рассчитать парный коэффициент корреляции. Воспользуемся следующими формулами:
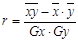 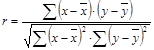
где:
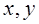 – индивидуальные значения факторного и результативного – индивидуальные значения факторного и результативного
признаков;
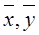 – средние значения признаков; – средние значения признаков;
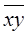 – средняя из произведений индивидуальных значений признаков; – средняя из произведений индивидуальных значений признаков;
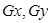 – средние квадратические отклонения признаков – средние квадратические отклонения признаков
1) Коэффициент рассчитаем по исходным данным варианта (50 предприятий), которые представлены в табл. 1
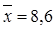 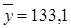 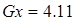 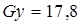
2) Расчет средней из произведений проведем в таблице M, заполняя данные о факторном и результативном признаке из таблицы №1:
| №
|
Группир. признак
|
Результат признак
|
X x Y
|
|
№
|
Группир
.
признак
|
Результат
признак
|
XxY
|
| число вагонов, шт./сут
|
чистая
прибыль, млн. руб.
|
|
число
вагонов,
шт./сут
|
чистая
прибыль,
млн. руб.
|
| 51
|
8
|
130
|
1040
|
|
76
|
10
|
134
|
1340
|
| 52
|
11
|
148
|
1628
|
|
77
|
6
|
136
|
816
|
| 53
|
36
|
155
|
5580
|
|
78
|
7
|
133
|
931
|
| 54
|
2
|
124
|
248
|
|
79
|
1
|
127
|
127
|
| 55
|
2
|
125
|
250
|
|
80
|
7
|
128
|
896
|
| 56
|
29
|
135
|
3915
|
|
81
|
1
|
118
|
118
|
| 57
|
14
|
126
|
1764
|
|
82
|
5
|
124
|
620
|
| 58
|
14
|
136
|
1904
|
|
83
|
15
|
137
|
2055
|
| 59
|
8
|
124
|
992
|
|
84
|
6
|
110
|
660
|
| 60
|
8
|
128
|
1024
|
|
85
|
17
|
139
|
2363
|
| 61
|
5
|
110
|
550
|
|
86
|
8
|
148
|
1184
|
| 62
|
8
|
150
|
1200
|
|
87
|
1
|
123
|
123
|
| 63
|
1
|
110
|
110
|
|
88
|
10
|
138
|
1380
|
| 64
|
6
|
122
|
732
|
|
89
|
21
|
189
|
3969
|
| 65
|
18
|
140
|
2520
|
|
90
|
11
|
139
|
1529
|
| 66
|
4
|
110
|
440
|
|
91
|
2
|
122
|
244
|
| 67
|
9
|
139
|
1251
|
|
92
|
2
|
124
|
248
|
| 68
|
2
|
121
|
242
|
|
93
|
1
|
113
|
113
|
| 69
|
1
|
111
|
111
|
|
94
|
8
|
117
|
936
|
| 70
|
5
|
132
|
660
|
|
95
|
6
|
126
|
756
|
| 71
|
1
|
129
|
129
|
|
96
|
3
|
130
|
390
|
| 72
|
7
|
139
|
973
|
|
97
|
3
|
112
|
336
|
| 73
|
9
|
148
|
1332
|
|
98
|
2
|
133
|
266
|
| 74
|
25
|
144
|
3600
|
|
99
|
25
|
195
|
4875
|
| 75
|
16
|
146
|
2336
|
|
100
|
5
|
176
|
880
|
| 61686
|
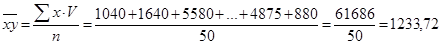
Расчет коэффициента корреляции проведем по первой из предложенных в начале решения двух формул:
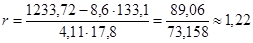
Вывод:
т.к. полученный коэффициент корреляции больше значения 0,8, то можно сделать вывод о том, что теснота связи между исследуемыми признаками достаточно тесная.
|