Министерство образования Республики Беларусь
Белорусский государственный экономический университет
Бобруйский филиал
Кафедра высшей математики и информатики
Ковальчук В.М.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Опорный конспект
Для студентов экономических специальностей
г. Бобруйск 2004
Лекция 1.
Предмет теории вероятностей. Случайные события и вероятности событий
Предметом теории вероятностей является анализ явлений, наблюдения над которыми не всегда приводят к одним и тем же исходам и в то же время обладающим некоторой статистической регулярностью, которая проявляется в статистической устойчивости частот исходов.
Статистическая устойчивость частот делает весьма правдоподобной гипотезу о возможности количественной оценки случайности того или иного события, появляющегося в результате эксперимента. Как правило, эксперимент предпринимается для изучения некоторых свойств интересующих нас экономического процесса или явления. При этом производится построение математической модели эксперимента, которое включает описание:
· Возможных исходов;
· Класса рассматриваемых событий;
· Вероятностей наступления этих событий.
Современная теория вероятностей основана на аксиоматическом подходе Колмогорова, позволяющим охватить все классические разделы теории вероятностей и дать основу для развития ее новых разделов, вызванных запросами практики.
Одной из важных сфер приложения теории вероятностей является экономика, так как при исследовании и прогнозировании экономических показателей используется эконометрика, опирающаяся на теорию вероятностей. Практическое значение вероятностных методов состоит в том, что они позволяют по известным характеристикам простых случайных явлений прогнозировать характеристики более сложных явлений.
.
1.1.
Случайные события. Вероятность.
Пространством элементарных событий
называют множество W взаимоисключающих исходов эксперимента такое, что каждый интересующий результат эксперимента может быть однозначно описан с помощью элементов этого множества. Элементы W называются элементарными событиями и обозначаются w.
Событием
называют любое подмножество AÍW элементов из W. Событие A произойдет, если произойдет какое-либо из элементарных событий wÎA. Пустое множество Æ называется невозможным событием.
Реклама

Суммой
двух событий A и B называется событие A+B(AÈB), состоящее из элементарных событий, принадлежащих хотя бы одному из событий A или B.
Произведением
двух событий A и B называется событие AB(AÇB), состоящих из элементарных событий, принадлежащих одновременно A и B.
Противоположным
событием событию A называют событие `A , состоящее из элементарных событий, не принадлежащих A.
Разностью
двух событий A и B называют событие A\B, состоящее из элементарных событий, которые входят в событие B.
События A и B называются несовместными
, если у них нет общих элементарных событий.
Пусть F - поле событий для данного эксперимента. Вероятностью
P(A) называется числовая функция, определенная на всех AÎF и удовлетворяющая трем условиям (аксиомам вероятностей):
1. P(A)³ 0;
2. P(W)=1;
3. Для любой конечной или бесконечной последовательности наблюдаемых событий 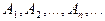 таких, что таких, что 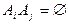 при при 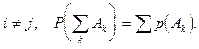
Существует 4 способа задания вероятности:
1.
Классический способ задания вероятности
При данном способе пространство элементарных событий является конечным, и все элементарные события равновероятны. Тогда вероятность события определяется равенством
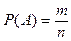 , ,
где 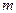 - число элементарных исходов испытания, благоприятствующих появлению события - число элементарных исходов испытания, благоприятствующих появлению события  ; ;
 - общее число возможных элементарных исходов испытания. - общее число возможных элементарных исходов испытания.
2. Геометрический способ задания вероятности
При данном способе пространство элементарных событий является бесконечным, но все элементарные события, входящие в это пространство, являются равновозможными.
Если отождествлять пространство элементарных событий с некоторой замкнутой областью пространства из 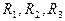 , то вероятность события , то вероятность события 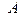 будет вычисляться по формуле будет вычисляться по формуле
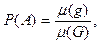
где 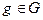 и и 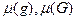 мера области : мера области :
· Это длина ( если рассматривается пространство 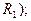
· площадь (если рассматривается пространство 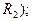
· объем ( если рассматривается пространство 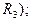
3.
Дискретный способ задания вероятности
При данном способе пространство элементарных событий является бесконечным счетным. Числовая неотрицательная функция Р определяется таким образом, чтобы вероятность каждого элементарного события была равна некоторому числу 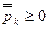 , ,
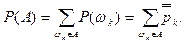
4.
Статистический способ задания вероятности
При данном способе рассматривается случайный эксперимент для которого построить пространство элементарных событий невозможно. Тогда эксперимент проводится 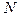 раз при неизменном комплексе условий протекания и подсчитывается число экспериментов, в которых появилось некоторое событие раз при неизменном комплексе условий протекания и подсчитывается число экспериментов, в которых появилось некоторое событие 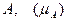 . Тогда вероятность вычисляется по формуле . Тогда вероятность вычисляется по формуле
Реклама

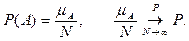
На практике, при вычислениях вероятностей в классической схеме часто приходиться пользоваться формулами комбинаторики (соединений).
Каждая из комбинаторных формул определяет общее число элементарных событий в некотором эксперименте, состоящем в выборе наудачу  элементов из элементов из  различных элементов исходного множества. Существуют две принципиально различные схемы выбора: различных элементов исходного множества. Существуют две принципиально различные схемы выбора:
а) без возращения элементов (это значит, что отбираются либо сразу все  элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества); элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества);
б) с возвращением (выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге и тщательном перемешиванием исходного множества перед следующим выбором).
В результате получаются различные постановки эксперимента по выбору наудачу  элементов из общего числа и различных элементов исходного множества. элементов из общего числа и различных элементов исходного множества.
1. Перестановки.
Возьмем 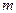 различных элементов различных элементов 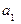 , ,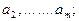 будем переставлять эти элементы всевозможными способами, оставляя неизменным их число и меняя лишь их порядок. Каждая из полученных таким образом комбинаций ( в том числе и первоначальная) носит название перестановки
. Общее число перестановок из будем переставлять эти элементы всевозможными способами, оставляя неизменным их число и меняя лишь их порядок. Каждая из полученных таким образом комбинаций ( в том числе и первоначальная) носит название перестановки
. Общее число перестановок из 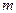 элементов обозначается элементов обозначается 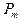 и равно и равно
Символ 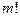 (читается «эм факториал»). Следует отметить, что 0!=1. (читается «эм факториал»). Следует отметить, что 0!=1.
2. Размещения
. Будем составлять из 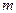 различных элементов множества по различных элементов множества по  элементов в каждом, отличающихся либо набором элементов, либо порядком их следования. Полученные при этом комбинации элементов называются размещениями
из элементов в каждом, отличающихся либо набором элементов, либо порядком их следования. Полученные при этом комбинации элементов называются размещениями
из 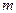 элементов по элементов по  и обозначается и обозначается 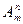 . Их общее число равно: . Их общее число равно:
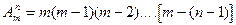 . .
Замечание.
Перестановки можно считать частным случаем размещений (именно размещениями из 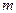 элементов по элементов по 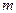 ) . ) .
3. Сочетания.
Из 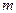 различных элементов будем составлять множества по различных элементов будем составлять множества по  элементов, имеющих различный состав. Полученная при этом комбинации элементов называются сочетаниями
из элементов, имеющих различный состав. Полученная при этом комбинации элементов называются сочетаниями
из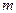 элементов по элементов по  . Общее число различных между собой сочетаний обозначается . Общее число различных между собой сочетаний обозначается 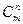 и вычисляется по следующим формулам: и вычисляется по следующим формулам:
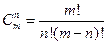 , ,
или
 . .
Лекция №2 Свойства вероятностей. Условная вероятность. Теоремы сложения и умножения вероятностей.
Пусть для некоторого случайного эксперимента построено пространство элементарных событий 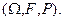 Числовая неотрицательная функция Числовая неотрицательная функция 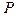 удовлетворяет следующим свойствам: удовлетворяет следующим свойствам:
1. Если события 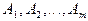 образуют полную группу событий, то вероятность объединения этих событий равна единице: образуют полную группу событий, то вероятность объединения этих событий равна единице: 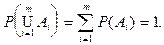
2. Вероятность противоположного события: 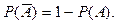
3. Если событие  влечет за собой событие влечет за собой событие  , то вероятность события , то вероятность события  не превосходит вероятность события не превосходит вероятность события 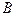 , т.е. , т.е. 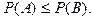
Пусть  и и 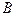 - наблюдаемые события в эксперименте , причем - наблюдаемые события в эксперименте , причем 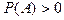 . Условной вероятностью . Условной вероятностью 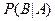 осуществления события осуществления события 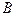 при условии, что событие при условии, что событие  произошло в результате данного эксперимента, называется величина, определяемая равенством: произошло в результате данного эксперимента, называется величина, определяемая равенством:
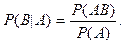
Теорема сложения:
Пусть событие 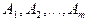 -совместные события. Тогда вероятность их объединения вычисляется по формуле: -совместные события. Тогда вероятность их объединения вычисляется по формуле:
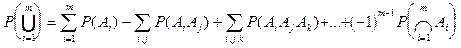 . .
Теорема умножения :
Вероятность произведения событий 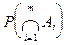 равна произведению вероятностей событий, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие имели место: равна произведению вероятностей событий, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие имели место:
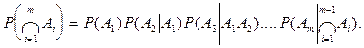
2.2. Формула полной вероятности. Формула Бейеса ( теорема гипотез)
Пусть случайный эксперимент можно описать событиями 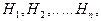 которые являются попарно несовместными которые являются попарно несовместными 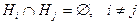 и и 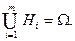 Такие события Такие события 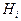 называют гипотезами
. Предполагается, что событие называют гипотезами
. Предполагается, что событие  может произойти с одной из гипотез может произойти с одной из гипотез 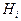 . .
Теорема:
Вероятность любого события  , которое может произойти с одной из гипотез , которое может произойти с одной из гипотез
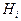 будет равна сумме произведений вероятностей гипотез на условную будет равна сумме произведений вероятностей гипотез на условную
вероятность события  : :
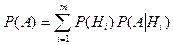 - формула полной вероятности. - формула полной вероятности.
Пусть случайный эксперимент можно описать попарно несовместными событиями 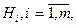 объединение которых образует пространство элементарных событий объединение которых образует пространство элементарных событий 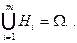 Событие Событие  может произойти с одной из гипотез. Предполагается, что в результате эксперимента произошло событие может произойти с одной из гипотез. Предполагается, что в результате эксперимента произошло событие  . Как изменится вероятность гипотез при этом? Ответ на поставленный вопрос дает следующая теорема. . Как изменится вероятность гипотез при этом? Ответ на поставленный вопрос дает следующая теорема.
Теорема:
Пусть событие  может произойти с одной из гипотез может произойти с одной из гипотез 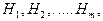
Которые описывают случайный эксперимент. Если в результате реализации
эксперимента произошло событие  , то вероятность гипотез вычисляются по , то вероятность гипотез вычисляются по
следующим формулам :
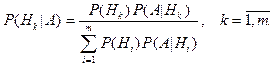 - формулы Байеса. - формулы Байеса.
Лекция №3 -5 Случайные величины. Функции распределения случайных величин
3.1. Дискретные случайные величины
Случайная величина , обозначаемая  , называется дискретной,
если она принимает , называется дискретной,
если она принимает
конечное либо счетное множество значений, т.е. множество -конечное, либо счетное. -конечное, либо счетное.
Законом распределения
дискретной случайной величины называется совокупность пар
чисел 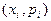 , где , где 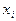 - возможные значения случайной величины, а - возможные значения случайной величины, а 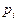 - вероятности, с - вероятности, с
которыми она принимает эти значения, причем 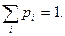
Зная закон распределения случайной величины, можно вычислить функцию распределения
:
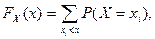
где суммирование распространяется на все значения индекса 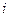 , для которых , для которых 
Математическим ожиданием
 дискретной случайной величины дискретной случайной величины  называется сумма произведений всех ее возможных значений и соответствующих им вероятностей: называется сумма произведений всех ее возможных значений и соответствующих им вероятностей:
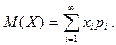
Модой
дискретной случайной величины, обозначаемой 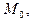 называется ее наиболее вероятное значение. называется ее наиболее вероятное значение.
Медианой
случайной величины  называется такое ее значение называется такое ее значение 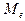 , для которого одинаково вероятно, окажется ли случайная величина меньше или больше , для которого одинаково вероятно, окажется ли случайная величина меньше или больше 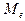 , т.е. , т.е.
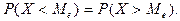
Дисперсией
случайной величины называется математическое ожиданиеквадрата ее отклонения:
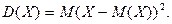
Дисперсия дискретной случайной величины вычисляется по формуле:
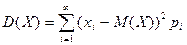 или или 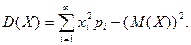
Средним квадратическим отклонением
(стандартом) случайной величины  называется арифметический корень из дисперсии, т.е. называется арифметический корень из дисперсии, т.е. 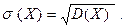
Начальным моментом
порядка 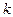 случайной величины случайной величины  называется математическое ожидание называется математическое ожидание 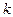 -й степени этой случайной величины, т.е. -й степени этой случайной величины, т.е. 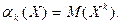
Для дискретной случайной величины 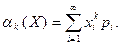
Центральным моментом
порядка 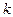 случайной величины случайной величины  называется математическое ожидание называется математическое ожидание 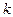 -й степени отклонения -й степени отклонения 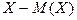 , т.е. , т.е. 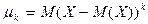 . .
Для дискретной случайной величины 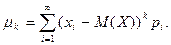
Биноминальным
называют закон распределения дискретной случайной величины  - числа появлений событий в - числа появлений событий в  независимых испытаниях, в каждом из которых вероятность появления события равна независимых испытаниях, в каждом из которых вероятность появления события равна 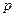 ; вероятность возможного значения ; вероятность возможного значения 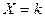 ( числа ( числа 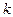 появлений события ) вычисляют по формуле Бернулли : появлений события ) вычисляют по формуле Бернулли : 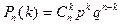 , где , где 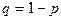 . При этом матема-тическое ожидание и дисперсия соответственно равны: . При этом матема-тическое ожидание и дисперсия соответственно равны: 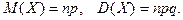
Наивероятнейшее число 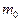 появлений событий в появлений событий в  независимых испытаниях определяется по формуле: независимых испытаниях определяется по формуле: 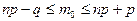
Если число испытаний велико, а вероятность появления события 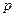 в каждом испытании мала, то вероятность того, что некоторое событие появиться в каждом испытании мала, то вероятность того, что некоторое событие появиться 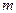 раз в раз в  испытаниях, приближенно вычисляется по формуле: испытаниях, приближенно вычисляется по формуле:
 , ,
где 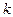 - число появлений событий в - число появлений событий в  независимых испытаниях, независимых испытаниях, 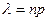 - среднее число появлений событий в - среднее число появлений событий в  испытаниях. Случайная величина, характеризующая число наступлений события испытаниях. Случайная величина, характеризующая число наступлений события  в в  независимых испытаниях, распределена по закону Пуассона
, если независимых испытаниях, распределена по закону Пуассона
, если 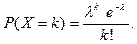
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона:
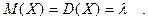
Геометрическое распределение
возникает в том случае, когда производится серия испытаний до первого появившегося события  . Тогда распределение случайной величины . Тогда распределение случайной величины  имеет вид: имеет вид:
Вероятность появления события  в каждом испытании постоянна и равна в каждом испытании постоянна и равна 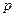 , т.е. , т.е.
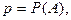 и и 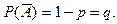
Математическое ожидание и дисперсия случайной величины, распределенной по геометрическому закону, соответственно равны:
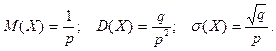
Гипергеометрический закон
распределения используется при проверке качества продукции. Проверяется 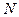 изделий, и известно, что среди этих изделий имеется изделий, и известно, что среди этих изделий имеется 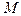 изделий, которые обладают некоторым признаком изделий, которые обладают некоторым признаком 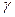 , а остальные , а остальные 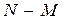 - признаком - признаком 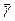 . Для проверки производится выборка, содержащая . Для проверки производится выборка, содержащая  изделий. Определить вероятность того, что среди этих изделий изделий. Определить вероятность того, что среди этих изделий 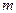 изделий обладают некоторым признаком изделий обладают некоторым признаком 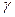 . Для определения вероятности используется классический способ задания вероятности. Число элементарных событий будет определяться числом сочетаний . Для определения вероятности используется классический способ задания вероятности. Число элементарных событий будет определяться числом сочетаний
 и и 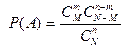 , ,
где  - событие, состоящее в том, что в выборке - событие, состоящее в том, что в выборке 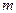 объектов обладают признаком объектов обладают признаком 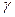 . .
Закон распределения дискретной случайной величины  , характеризующей число появлений события , характеризующей число появлений события 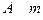 раз в раз в 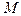 испытаниях имеет вид: испытаниях имеет вид:
· Если 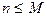
· Если 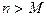
Функция гипергеометрического распределения имеет вид
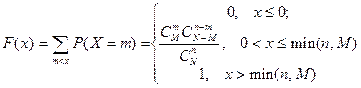
Гипергеометрический закон стремится к биноминальному закону распределению, если 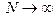 при при 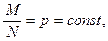 и его числовые характеристики следующие и его числовые характеристики следующие
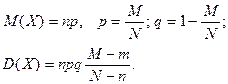
3.2.
Непрерывные случайны величины.
Случайная величина  называется непрерывной,
если существует такая неотрицательная, называется непрерывной,
если существует такая неотрицательная,
интегрируемая по Риману функция 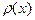 , называемая плотностью распределения вероятностей, , называемая плотностью распределения вероятностей,
что при всех 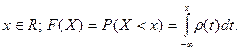 Множество значений непрерывной Множество значений непрерывной
случайной величины   - некоторый числовой интервал. - некоторый числовой интервал.
Плотностью распределения вероятностей
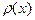 непрерывной случайной величиныХ непрерывной случайной величиныХ
называют предел, если он существует, отношения вероятности попадания случайной величины
Х на отрезок 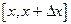 , примыкающей к точке , примыкающей к точке 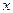 , к длине этого отрезка, когда , к длине этого отрезка, когда
последний стремится к 0, т.е.
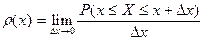 . .
Свойства плотности распределения вероятностей:
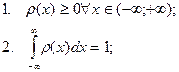
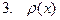 -
непрерывная или кусочно непрерывна функция; -
непрерывная или кусочно непрерывна функция;
Функция распределения
случайной величины  – это функция – это функция 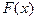 действительной действительной
переменной 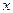 , определяющая вероятность того, что случайная величина принимает значение , определяющая вероятность того, что случайная величина принимает значение
меньше некоторого фиксированного числа 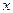 , т.е. , т.е. 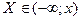
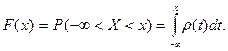
Математическое ожидание и дисперсия случайной величины :
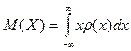 ; ;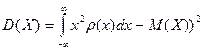 ; ; 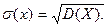
Модой
непрерывной случайной величины  называется действительное число называется действительное число  , ,
определяемое точка максимума плотности распределения вероятностей  . .
Медианой
непрерывной случайной величины  называется действительное число называется действительное число 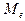 , ,
Удовлетворяющее условию 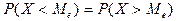 , т.е. корень уравнения , т.е. корень уравнения
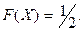
Начальный момент
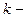 го порядка: го порядка:
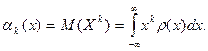
Центральный момент
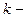 го порядка: го порядка:
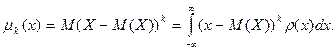
Коэффициент асимметрии
или «скошенности» распределения
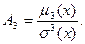
Коэффициент эксцесса
или островершинности распределения
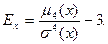
Случайная величина  называется центрированной, если называется центрированной, если 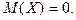 Если же для Если же для
случайной величины  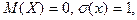 то она называется центрированной и то она называется центрированной и
нормированной (стандартизованной) случайной величиной.
3.3. Законы распределения непрерывной случайной величины
Равномерное распределение:
Пусть плотность вероятности равна нулю всюду, кроме отрезка 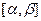 , на котором все значения случайной величины Х одинаково возможны. Выражение плотности распределения вероятностей , на котором все значения случайной величины Х одинаково возможны. Выражение плотности распределения вероятностей 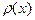 имеет следующий вид: имеет следующий вид:
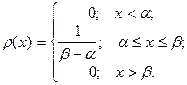
Функция равномерного распределения задается формулой:
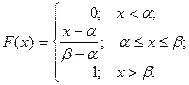
Математическое ожидание, дисперсия и среднее квадратическое отклонение соответственно равны:
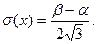
Показательное распределение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины  , которое описывается функцией плотности вероятности: , которое описывается функцией плотности вероятности:
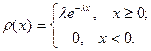
где 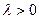 постоянная и называется параметром экспоненциального распределения. постоянная и называется параметром экспоненциального распределения.
Функция распределения случайной величины, распределенной по показательному закону, имеет вид:
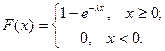
Математическое ожидание 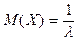 . Дисперсия . Дисперсия 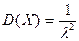 , среднее квадратическое отклонение , среднее квадратическое отклонение 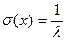 . .
Лекция №6. Нормальное распределение.
Распределение с непрерывной случайной величины называется нормальным, если плотность распределения ее описывается формулой:
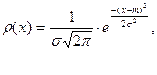
где 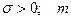 - параметры распределения. - параметры распределения.
Функция распределения случайной величины Х, распределенной по нормальному закону:
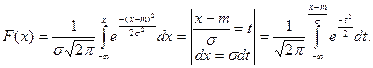
Полученный интеграл нельзя выразить через элементарные функции, но его можно вычислить через специальную функцию:
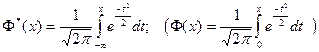 , ,
называемую нормальной функцией распределения (функцией Лапласа). Эта функция неубывающая, непрерывная слева и 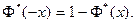 Математическое ожидание и дисперсия соответственно равны Математическое ожидание и дисперсия соответственно равны 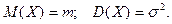
Центральные моменты случайной величины с нормальным законом распределения вычисляются через следующие рекуррентные соотношения:
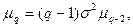
поскольку 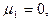 то нечетные центральные моменты равны нулю, а четные центральные моменты равны: то нечетные центральные моменты равны нулю, а четные центральные моменты равны: 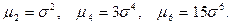
Коэффициенты ассиметрии и эксцесса для нормального закона распределения равны нулю:
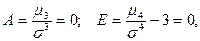
так как они характеризуют скошенность и крутизну исследуемового закона распределения по сравнению с нормальным.
Вероятность попадания случайной величины  , подчиненной нормальному закону распределения, на заданный интервал , подчиненной нормальному закону распределения, на заданный интервал 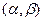 , определяется следующим образом: , определяется следующим образом:
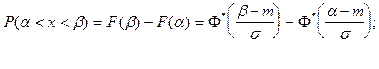
или
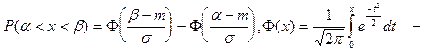 функция Лапласа. функция Лапласа.
Вероятность заданного отклонения вычисляется по формуле:
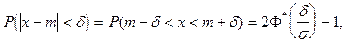 или или
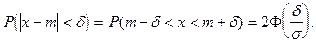
Интервалом практически возможных значений случайной величины  , распределенной по нормальному закону , будет интервал , распределенной по нормальному закону , будет интервал 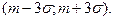
Лекция 7-8. Предельные теоремы и законы больших чисел
Все законы вероятности получены из практики, то есть из наблюдений за массовыми случайными явлениями. Массовые случайные явления проявляются в статистической совокупности.
Было замечено, что при определенных условиях массовые случайные явления порождают величину неслучайную, которая подчиняется вполне определенным закономерностям. Все полученные соответствующие теоремы и образуют теоремы закона больших чисел, в которых приведены условия, когда среднее значение случайных величин стремится к величине не случайной. Таким образом, закон больших чисел – это совокупность теорем, в которых приведены условия, при которых последовательность случайных величин подчиняется определенным закономерностям, то есть стремится к величине неслучайной.
Неравенство Чебышева
:
Теорема:
Вероятность того, что случайная величина  отклоняется от своего математического отклоняется от своего математического
ожидания на величину не меньше 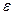 , ограничена сверху величиной , ограничена сверху величиной 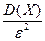 , где , где 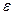 - -
положительное действительное число:
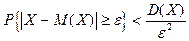 или или 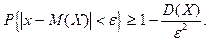
Теорема Чебышева (закон больших чисел).
Теорема:
Если 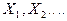 последовательность независимых случайных величин, которые имеют последовательность независимых случайных величин, которые имеют
конечное математические ожидания и ограниченные дисперсии 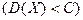 , то , то
средние арифметические наблюденных значений случайных величин сходиться по
вероятности к среднему арифметическому их математических ожиданий:
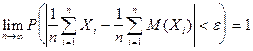 . .
Закон больших чисел справедлив и для зависимых случайных величин, то есть справедлива
теорема Маркова:
Теорема: :
Если для случайных величин 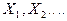 выполняется условие выполняется условие
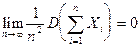 , то среднее арифметическое наблюденных случайных величин , то среднее арифметическое наблюденных случайных величин
сходится по вероятности к среднему арифметическому их математических ожиданий:
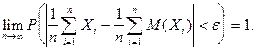
Теоремы Бернулли :
Если производится  испытаний, в каждом из которых некоторое событие испытаний, в каждом из которых некоторое событие
 может появиться с вероятностью может появиться с вероятностью 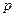 , то относительная частота появления , то относительная частота появления
события в  испытаниях сходится по вероятности к вероятности появления испытаниях сходится по вероятности к вероятности появления
события в каждом испытании:
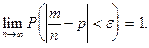
Теорема Пуассона:
Пусть производится  независимых испытаний, в каждом их которых событие независимых испытаний, в каждом их которых событие
 появляется с вероятностью появляется с вероятностью 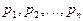 . Тогда при неограниченном . Тогда при неограниченном
увеличении числа испытаний относительная частота появления события 
сходится по вероятности к среднему арифметическому вероятности
появления события в различных испытаниях:
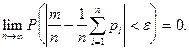
Теорема Лендеберга-Леви:
Пусть 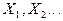 независимые одинаково распределенные случайные независимые одинаково распределенные случайные
величины с математическим ожиданием 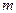 и дисперсией и дисперсией  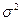 . Закон . Закон
распределения нормируемой случайной величины 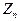 стремится к нормальному стремится к нормальному
закону распределения с плотностью распределения вероятностей равной
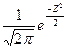 , ,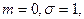 где где
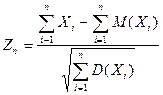 - нормированная случайная величина.
- нормированная случайная величина.
Это центральная предельная теорема для одинаково распределенных случайных независимых величин.
Теорема Ляпунова:
Если 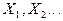 независимые случайные величины, имеющие конечные независимые случайные величины, имеющие конечные
математические ожидания 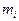 и дисперсии и дисперсии 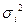 и абсолютные центральные и абсолютные центральные
моменты третьего порядка, удовлетворяющие условиям:
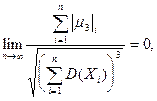
то закон распределения величины 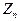 сходится к нормальному закону сходится к нормальному закону
распределения с плотностью распределения вероятности
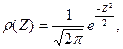 для которой для которой 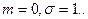
Эта теорема имеет большое практическое значение, так как, используя ее, можно вычислить вероятность того, что сумма независимых случайных величин принимает значение, принадлежащее интервалу. Условие
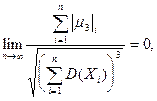 характеризует тот факт, что все случайные величины сравнимы между собой, то есть ни одна из случайных величин не имеет преимущество перед другими случайными величинами. характеризует тот факт, что все случайные величины сравнимы между собой, то есть ни одна из случайных величин не имеет преимущество перед другими случайными величинами.
Рассмотрим дискретную случайную величину  , которая характеризует число появлений события , которая характеризует число появлений события  в в  независимых испытаниях. Эту случайную величину можно представить в виде суммы случайной величины независимых испытаниях. Эту случайную величину можно представить в виде суммы случайной величины 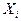 , каждая из которых характеризует число появлений события , каждая из которых характеризует число появлений события  в в 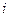 испытании. Нормированная сумма будет иметь вид: испытании. Нормированная сумма будет иметь вид: 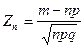 . .
Если случайная величина  подчиняется биноминальному закону распределения, то вычисление вероятности того, что некоторое событие подчиняется биноминальному закону распределения, то вычисление вероятности того, что некоторое событие  появиться появиться 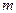 раз в раз в  испытаниях по формуле Бернулли затруднительно, если испытаниях по формуле Бернулли затруднительно, если  достаточно большое, а достаточно большое, а 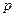 мало. В этом случае можно воспользоваться следующими теоремами: мало. В этом случае можно воспользоваться следующими теоремами:
Теорема Мавра -Лапласа (локальная):
Пусть производится  испытаний, в каждом из которых испытаний, в каждом из которых
некоторое событие  может появиться с вероятностью может появиться с вероятностью 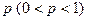 . Тогда для всех . Тогда для всех 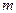 , удовлетворяющих условию , удовлетворяющих условию 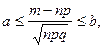 ( где ( где 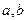 - произвольные числа) выполняется соотношение: - произвольные числа) выполняется соотношение:
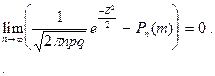
Локальная теорема используется при больших значениях  для вычисления для вычисления 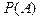 , где некоторое событие , где некоторое событие  наступает наступает 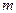 раз в раз в  испытаниях. испытаниях.
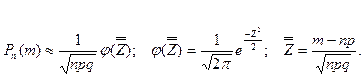
Теорема Муавра- Лапласа (интегральная):
Пусть производится  независимых испытаний, независимых испытаний,
в каждом из которых событие может появиться с вероятностью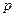 . Тогда для любых . Тогда для любых 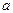 и и 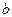
справедливо соотношение:
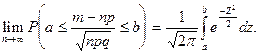
Из предельного равенства теоремы следует формула:
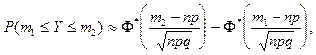
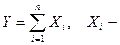 число появлений событий число появлений событий  в в  испытаниях. испытаниях.
Отсюда вытекают следующие соотношения:
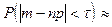 2Ф* 2Ф*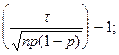
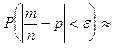 2Ф* 2Ф*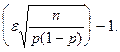
В отличии от теорем Бернулли и Пуассона последние две формулы более точную оценку
вероятности отклонений частоты появления событий от его математического ожидания и
частости события от вероятности появления события в каждом испытании.
Двумерные случайные величины.
Совокупность случайных величин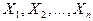 образуют образуют 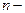 мерную случайную мерную случайную
величину 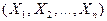 . Если экономический процесс описывается при помощи двух . Если экономический процесс описывается при помощи двух
случайных величин 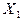 и и 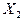 , определяется двумерная случайная величина , определяется двумерная случайная величина 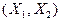 или или
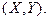
Функция распределения
системы двух случайных величин 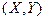 , рассматриваемой как , рассматриваемой как
функция переменных 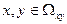 , называется вероятность появления события , называется вероятность появления события
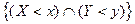 : :
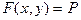 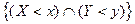 . .
Используя функцию распределения, можно найти вероятность попадания случайной точки в
бесконечную полуполосу 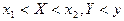 или или 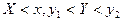 и прямоугольник и прямоугольник
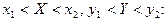
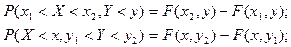 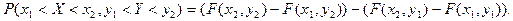
Дискретной
называют двухмерную величину, составляющие которой дискретны.
Законом распределения
двумерной дискретной случайной величины называется множество
всевозможных значений 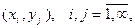 дискретных двумерных случайных величин и
дискретных двумерных случайных величин и
соответствующих им вероятностей  При этом При этом 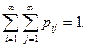
Непрерывной
называют двумерную величину, составляющие которой непрерывны.
Функция 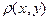 , равная пределу отношения вероятности попадания двумерной случайной , равная пределу отношения вероятности попадания двумерной случайной
величины 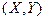 в прямоугольник со сторонами в прямоугольник со сторонами 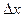 и и 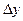 к площади этого прямоугольника, к площади этого прямоугольника,
когда обе стороны прямоугольника стремятся к нулю, называется плотностью распределения
вероятностей:
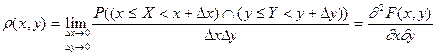 . .
Зная плотность распределения, можно найти функцию распределения по формуле:
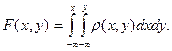
Вероятность попадания случайной точки 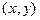 в область в область 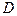 определяется равенством: определяется равенством:
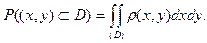
Вероятность того, что случайная величина  приняла значение приняла значение 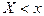 при условии, что при условии, что
случайная величина 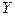 приняла фиксированное значение, вычисляется по формуле: приняла фиксированное значение, вычисляется по формуле:
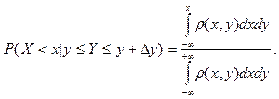
Начальным моментом
порядка 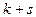 системы системы 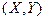 называется математическое называется математическое
ожидание произведений 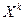 и и 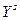 , т.е. , т.е. 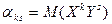 .Если .Если  и и 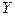 -дискретные -дискретные
случайные величины, то
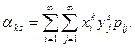
Если  и и 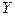 - непрерывные случайные величины, то - непрерывные случайные величины, то
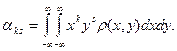
Центральным моментом
порядка 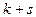 системы системы 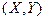 называется математическое называется математическое
ожидание произведений 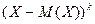 и и 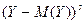 , т.е. , т.е.
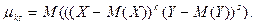
Если составляющие величины являются дискретными, то
Если составляющие величины являются непрерывными, то
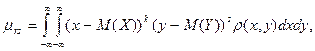 где где
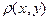 - плотность распределения системы - плотность распределения системы 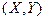 . .
Условным математическим ожиданием
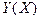 при при  ( при ( при 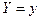 ) называется ) называется
выражение вида:
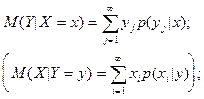 -для дискретной случайной величины -для дискретной случайной величины 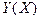
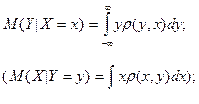 - для непрерывной случайной величины - для непрерывной случайной величины 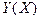 . .
Корреляционным моментом
независимых случайных величин  и и 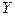 , входящих в , входящих в
двумерную случайную величину 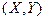 , называют математическое ожидание произведений , называют математическое ожидание произведений
отклонений этих величин:
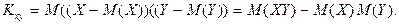
Корреляционный момент двух независимых случайных величин  и и 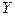 , входящих в , входящих в
двумерную случайную величину 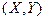 , равен нулю. , равен нулю.
Коэффициентом корреляции 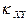 случайных величин
случайных величин  и и 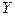 , входящих в , входящих в
двумерную случайную величину 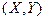 , называют отношение корреляционного момента к , называют отношение корреляционного момента к
произведению средних квадратических отклонений этих величин:
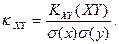
Коэффициент корреляции удовлетворяет условию 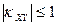 и определяет степень линейной и определяет степень линейной
зависимости между  и и  . Случайные величины, для которых . Случайные величины, для которых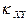 =
0 , называются =
0 , называются
некоррелированными.
Уравнения 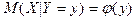 и и 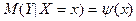 называют уравнениями регрессии, а линии, определяемые ими, - линиями регрессии. называют уравнениями регрессии, а линии, определяемые ими, - линиями регрессии.
Лекция №9.Случайные функции. Цепи Марков. Пуассоновский поток событий
Пусть 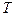 - некоторое множество действительных чисел. Если каждому значению - некоторое множество действительных чисел. Если каждому значению 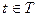 поставлена в соответствие случайная величина поставлена в соответствие случайная величина 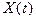 , то на множестве , то на множестве 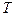 задана случайная функция задана случайная функция
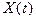 . .
Если 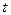 - время, то случайная функция называется случайным процессом. - время, то случайная функция называется случайным процессом.
Значение случайной функции 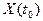 при при 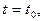 где где 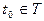 , называется сечением. Каждое испытание дает конкретную функцию , называется сечением. Каждое испытание дает конкретную функцию 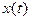 , которая называется реализацией (траекторией) случайной функции. , которая называется реализацией (траекторией) случайной функции.
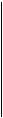   XX сечение XX сечение
0 t 0 tt
Реализация Семейство реализаций
При зафиксированном значении аргумента t случайная функция X(t) превращается в случайную величину- сечение
случайной функции или процесса. Тогда X(t) в данный момент времени t определяется плотностью распределения f(x ; t). Однако одномерные законы распределения и их числовые характеристики, вычисленные для одного момента времени ( для одного сечения семейства реализаций) не могут оценивать характер изменения процесса во времени. Для этой цели используют характеристики связи между ординатами, взятыми в различные моменты времени. Наиболее полно эти связи характеризуются многомерной плотностью распределения 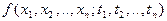 n произвольных сечений процесса. Однако многомерная плотность распределения не всегда известна, поэтому для практических приложений случайные процессы характеризуются математическим ожиданием, дисперсией и корреляционной функцией. n произвольных сечений процесса. Однако многомерная плотность распределения не всегда известна, поэтому для практических приложений случайные процессы характеризуются математическим ожиданием, дисперсией и корреляционной функцией.
Математическим
ожиданием случайной функцией 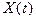 называют неслучайную функцию называют неслучайную функцию 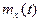 , которая при каждом значении аргумента , которая при каждом значении аргумента 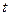 равна математическому ожиданию соответствующего сечения семейства реализаций случайной функции: равна математическому ожиданию соответствующего сечения семейства реализаций случайной функции:
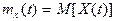
и является средней траекторией для всех возможных реализаций.
Дисперсией
случайной функции 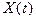 называют неслучайную функцию называют неслучайную функцию 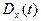 , значения которой для каждого , значения которой для каждого 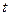 равно дисперсии соответствующего сечения случайной функции: равно дисперсии соответствующего сечения случайной функции:
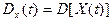
и характеризующей возможный разброс реализаций случайной функции относительно средней траектории.
Корреляционной
функцией случайной функции 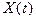 называют неслучайную функцию двух аргументов называют неслучайную функцию двух аргументов 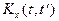 , которая при каждой паре значений , которая при каждой паре значений 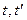 равна корреляционному моменту соответствующих сечений случайной функции: равна корреляционному моменту соответствующих сечений случайной функции:
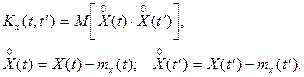
Корреляционная функция характеризует степень зависимости между сечениями случайной функции, относящихся к различным  . Положительное значение корреляционной функции свидетельствует о том, что при увеличении (уменьшении) ординат процесса в сечении . Положительное значение корреляционной функции свидетельствует о том, что при увеличении (уменьшении) ординат процесса в сечении  в среднем увеличиваются (уменьшаются) ординаты при в среднем увеличиваются (уменьшаются) ординаты при  . Отрицательная корреляция означает увеличение (уменьшение) в среднем ординат в сечении . Отрицательная корреляция означает увеличение (уменьшение) в среднем ординат в сечении 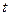 при их уменьшении (увеличении) в сечении при их уменьшении (увеличении) в сечении 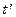 . .
Корреляционная функция является симметричной функцией своих аргументов, а ее ординаты по абсолютному значению не могут быть больше произведений среднеквадратичных отклонений в моменты времени 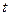 и и 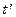 : :
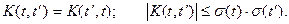
Процесс считается стационарным
, если его многомерная плотность распределения не изменяется при сдвиге соответствующих моментов времени на любую величину. В рамках корреляционной теории , процесс считается стационарным, если его ковариационная функция 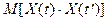 не зависит от времени, а зависит только от разности не зависит от времени, а зависит только от разности 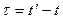 , ,
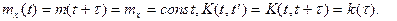
Корреляционная функция стационарного процесса по модулю не превосходит дисперсию:
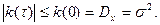
Стационарный процесс у которого корреляционная функция стремится к нулю 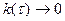 при при 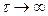 называют эргодичным.
Эргодические процессы представляют наибольший интерес для практических приложений, поскольку их характеристики, определяемые по семейству и по одной реализации совпадают: называют эргодичным.
Эргодические процессы представляют наибольший интерес для практических приложений, поскольку их характеристики, определяемые по семейству и по одной реализации совпадают:
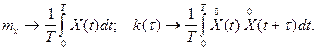
Марковскими
случайными процессами называют такие процесса, у которых плотность совместного распределения произвольных двух сечений полностью определяют характер процессов, т.е. дальнейшее поведение процесса зависит только от значений, принятых процессом в настоящий момент времени , и не зависит от ранее принятых.
Марковский случайный процесс, в котором сама функция принимает счетное множество возможных состояний (дискретные состояния)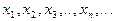 , переход из одного состояния в другое происходит скачком под влиянием случайных факторов, называют цепями Маркова
. Если переход из состояния в состояние происходит в дискретные моменты времени , переход из одного состояния в другое происходит скачком под влиянием случайных факторов, называют цепями Маркова
. Если переход из состояния в состояние происходит в дискретные моменты времени 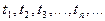 , то такой процесс называют дискретными цепями Маркова
. Если переходы возможны в любой момент времени, то процесс называют непрерывными цепями Маркова
. , то такой процесс называют дискретными цепями Маркова
. Если переходы возможны в любой момент времени, то процесс называют непрерывными цепями Маркова
.
Вероятность того, что дискретная цепь Маркова в момент времени 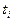 примет значение примет значение 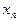 при условии, что в момент времени при условии, что в момент времени 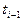 она имела значение она имела значение 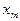 , называют вероятностью перехода
из состояние в состояние , называют вероятностью перехода
из состояние в состояние 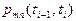 . Если эта вероятность зависит от длины промежутка времени . Если эта вероятность зависит от длины промежутка времени 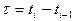 и нет зависит от начала отсчета времени, т.е. не зависит от номера шага, то такую цепь Маркова называют однородной: и нет зависит от начала отсчета времени, т.е. не зависит от номера шага, то такую цепь Маркова называют однородной:
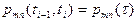 . .
Дискретные цепи Маркова однозначно определяются либо матрицей переходов
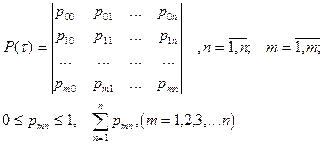
или графом состояний
    Р21
Р32
Р43 Р21
Р32
Р43
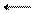   Х1
Х2
Х3
Х4 Х1
Х2
Х3
Х4
Р12
Р23
Р34
Вектором вероятностей
(безусловной вероятностью) состояния цепи Маркова называют вероятности 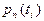 того, что в момент времени того, что в момент времени 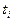 цепь примет значение цепь примет значение 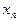 , которая представляет собой матрицу-строку: , которая представляет собой матрицу-строку:
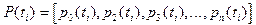 , ,
где - 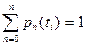 . .
Вектор вероятностей состояния однородной цепи Маркова после 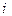 этапов однозначно определяется вектором вероятностей этапов однозначно определяется вектором вероятностей 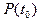 в начальный момент времени матрицей переходов в начальный момент времени матрицей переходов 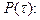 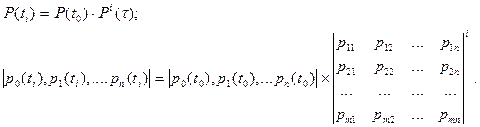
Если в цепи Маркова 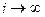 , то вектор вероятностей состояния превращается в вектор финальной (стационарной) вероятности , то вектор вероятностей состояния превращается в вектор финальной (стационарной) вероятности 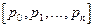 , определяемый из однородной системы n уравнений: , определяемый из однородной системы n уравнений:
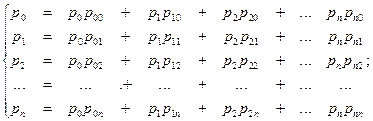
Учитывая, что  и заменяя этим соотношение одно из вышеприведенных уравнений в системе, находим искомые финальные (стационарные) вероятности однородной цепи Маркова. и заменяя этим соотношение одно из вышеприведенных уравнений в системе, находим искомые финальные (стационарные) вероятности однородной цепи Маркова.
Для непрерывных цепей Маркова возможности перехода из состояния 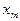 в состояние в состояние 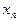 за время за время 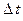 оценивается плотностью вероятностей
перехода оценивается плотностью вероятностей
перехода 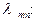
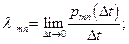 при условии, что при условии, что 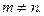
Если  не зависит от времени, то непрерывная цепь Маркова называется однородной. не зависит от времени, то непрерывная цепь Маркова называется однородной.
Для непрерывных цепей Маркова вектор вероятностей состояния есть функция времени и определяется путем решения системы дифференциальных уравнений, которые составляются по графу состояния цепи Маркова по следующим правилам :
· в левой части каждого уравнения стоят производные по времени вероятностей состояния цепи;
· правая часть этих уравнений содержит столько членов, сколько переходов (стрелок на графе) связанно с данным состоянием;
· каждый член правой части уравнений равен произведению плотности вероятностей перехода , соответствующей данной стрелки графа состояния, умноженной на вероятность того состояния из которого исходит стрелка;
· каждый член правой части уравнений имеет знак «минус», если стрелка графа состояния входит в данное состояния и знак «плюс», если стрелка выходит из данного состояния.
Например:
Имеем граф состояния однородной непрерывной цепи ркова:

X1
  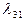 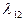
  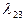
 X3
X2 X3
X2
Для этого графа составляем систему уравнений по вышеуказанным правилам:
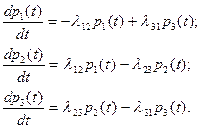
Учитывая, что 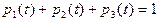 , известными методами находят , известными методами находят 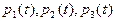 . .
В случае, когда нас интересую вероятности состояния непрерывных цепей Маркова по истечению длительного промежутка времени (установившейся процесс 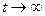 ), то решение системы получают путем записи в левой части системы дифференциальных вместо производных нулей, т.е. : ), то решение системы получают путем записи в левой части системы дифференциальных вместо производных нулей, т.е. :
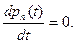
Переход из состояния в состояние в непрерывных цепях Маркова происходит вод воздействием потока событий.
Потоком событий
называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.
Поток событий называю простейшим или стационарным Пуассоновским, если он стационарен, ординарен и без последействия.
1. Поток называется стационарным, если вероятность попадания события на участок времени 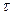 зависит только от длины этого участка и не зависит от места расположения этого участка на оси времени. зависит только от длины этого участка и не зависит от места расположения этого участка на оси времени.
2. Поток называют потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от числа событий на другом участке.
3. Поток событий называют ординарным, если вероятность попадания на элементарный участок двух и более событий пренебрежительно мала по сравнению с вероятностью попадания на этот участок одного события.
Плотностью вероятностей
перехода 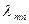 цепи Маркова из состояния цепи Маркова из состояния 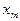 в состояние в состояние 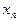 является интенсивностью потока событий является интенсивностью потока событий 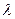 или средним числом событий в единицу времени. Для стационарного потока
или средним числом событий в единицу времени. Для стационарного потока 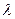 не зависит от времени. Для нестационарного
не зависит от времени. Для нестационарного 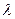 - функция времени
- функция времени 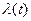 . .
В Пуассоновском потоке событий число событий, попадающих на любой участок времени 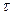 , подчиняется закону распределения Пуассона с математическим ожиданием , подчиняется закону распределения Пуассона с математическим ожиданием 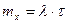 , т.е. вероятность того, что за время , т.е. вероятность того, что за время 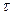 произойдет ровно произойдет ровно 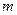 событий, равна: событий, равна:
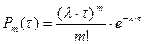 . .
Промежутки времени 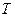 между событиями в Пуассоновском потоке событий подчиняются показательному закону распределения с функцией распределения между событиями в Пуассоновском потоке событий подчиняются показательному закону распределения с функцией распределения 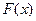 и плотностью распределения и плотностью распределения 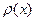 , равные: , равные:
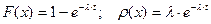 , ,
с математическим ожиданием 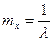 , дисперсией , дисперсией 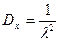 и среднеквадратичным отклонением и среднеквадратичным отклонением 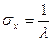 . .
Лекция №10. Предмет математической статистики. Генеральная и выборочная совокупности. Вариационные ряды и их характеристики
Математическая статистика –
раздел высшей математики, изучающий методы сбора, систематизации и обработки результатов случайных массовых явлений с целью выявления существующих закономерностей.
Вся подлежащая изучению совокупность объектов наблюдений называют генеральной совокупностью.
Иными словами, совокупность всех возможных, всех мыслимых, значений исследуемой случайной величины. Понятие генеральной совокупности аналогично понятию случайной величины (закону распределения, вероятностному пространству).
Та часть объектов, которая отобрана для непосредственного изучения из генеральной совокупности, называется выборочной совокупностью или выборкой.
Число объектов в генеральной или в выборочной совокупности называют их объемом 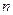 . .
Основная форма представления выборочной совокупности – вариационные ряды. Вариационный ряд
– это ранжированные в порядке возрастания или убывания ряд вариантов с соответствующими им весами (частотами и частостями). Различные значения признака (случайной величины 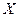 ) называют вариантами (обозначаем их через ) называют вариантами (обозначаем их через 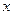 ). Число, показывающее, сколько раз встречается в выборке вариант ). Число, показывающее, сколько раз встречается в выборке вариант 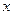 , называют частотой варианта , называют частотой варианта 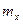 . Отношение числа вариантов к объему выборки (или общему числу наблюдений) . Отношение числа вариантов к объему выборки (или общему числу наблюдений)  - называют частостью варианта и обозначают - называют частостью варианта и обозначают  : :
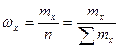 . .
Частости и частоты еще называют весами.
Кроме частости и частоты используют понятие накопленной частости и частоты,
которые обозначают 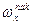 и и 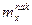 соответственно. Накопленная частота показывает, сколько вариантов признака приняли значение меньше заданного значения соответственно. Накопленная частота показывает, сколько вариантов признака приняли значение меньше заданного значения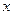 . .
Если варианты не отличаются друг от друга меньше определенного значения- то такой ряд называют дискретным.
Если варианты отличаются друг от друга на сколь угодно малую величину, то такой ряд называют непрерывным.
Для построения непрерывного вариационного ряда рекомендуемое число интервалов 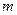 вычисляют по формуле Стерджеса вычисляют по формуле Стерджеса 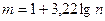 , а ширина интервала , а ширина интервала 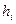 равна: равна:
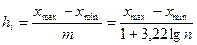 , ,
где 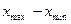 - разность между наибольшим и наименьшим значением признака. За начало первого интервала рекомендуется принимать величину - разность между наибольшим и наименьшим значением признака. За начало первого интервала рекомендуется принимать величину 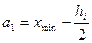 . Начало второго интервала совпадает с концом второго . Начало второго интервала совпадает с концом второго 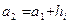 и т.д., до тех пор, пока начало и т.д., до тех пор, пока начало  -ого интервала не будет больше -ого интервала не будет больше 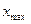 . .
Графически вариационные ряды изображают в виде полигона и гистограммы.
Полигон существуют для дискретного вариационного ряда в виде зависимости 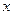 от от 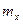 или или 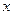 от от 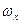 .Гистограмма представляет собой графики прямоугольников шириной равной величине интервала .Гистограмма представляет собой графики прямоугольников шириной равной величине интервала 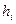 и высотой равной частоте или частости попадания ( и высотой равной частоте или частости попадания (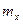 или или 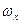 ) признака в этот интервал. ) признака в этот интервал.
Зависимость между 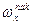 или или 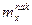 и и 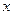 называют кумулятивной кривой или кумулятой. По своей сути полигон является статистическим аналогом или оценкой многоульника распределения случайной величины. Гистограмма – эмпирическая функции плотности распределения, кумулята - эмпирическая функция распределения. называют кумулятивной кривой или кумулятой. По своей сути полигон является статистическим аналогом или оценкой многоульника распределения случайной величины. Гистограмма – эмпирическая функции плотности распределения, кумулята - эмпирическая функция распределения.
Вариационные ряды характеризуются показателями средних значений и вариации. К средним значениям относят:
- средняя арифметическая  вариационного ряда, равная: вариационного ряда, равная:
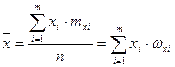 , ,
где 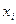 - варианты дискретного ряда или середины интервалов интервального ряда, - варианты дискретного ряда или середины интервалов интервального ряда, 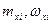 - соответствующие частоты или частости вариантов или интервалов. - соответствующие частоты или частости вариантов или интервалов.
- средней степенной 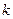 - ого порядка: - ого порядка:
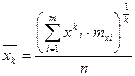 . .
При 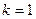 получаем среднюю арифметическую; получаем среднюю арифметическую;
при 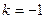
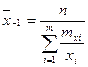 - среднюю гармоническую; - среднюю гармоническую;
при 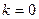 ( после открытия неопределенности ( после открытия неопределенности 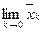 ): ):
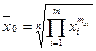 - среднюю геометрическую; - среднюю геометрическую;
при 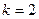 : :
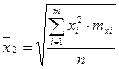 - средняя квадратическая. - средняя квадратическая.
Перечисленные средние относят к аналитическим. Кроме них в статистическом анализе применяют структурные или порядковые средние. К ним относят медиану
и моду
.
Медианой
вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений.
Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов – полусумме двух серединных вариантов. Приближенно медиану можно найти с помощью кумуляты как значение признака, для которого
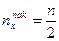 или или 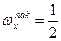 . .
Модой
вариационного ряда называют вариант, которому соответствует наибольшая частота.
К показателям вариации вариационных рядов относят:
- вариационный размах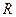 ,
равный разности между наибольшим и наименьшим вариантами ряда: ,
равный разности между наибольшим и наименьшим вариантами ряда:
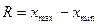 ; ;
- выборочная (эмпирическая) дисперсия 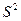 , равная средней арифметической квадратов отклонений вариантов от их средних арифметических:
, равная средней арифметической квадратов отклонений вариантов от их средних арифметических:
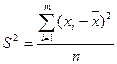 или или 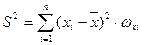 ; ;
- среднее квадратическое
отклонение 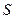 : :
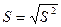 ; ;
-
коэффициент вариации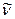 ,
равный процентному отношению среднего квадратического отклонения к средней арифметической: ,
равный процентному отношению среднего квадратического отклонения к средней арифметической:
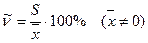

Лекция 11. Связь между генеральной и выборочной совокупностью.
Понятие генеральной совокупности в определенном смысле аналогично понятию случайной величины (закону распределения, вероятностному пространству). Выборку можно рассматривать, как некий эмпирический аналог генеральной совокупности.
Средние арифметические распределения признака в генеральной и выборочной совокупностях называются соответственно генеральной
и выборочной средними.
Дисперсии этих распределений называют генеральной
и выборочной дисперсиями.
Отношение числа элементов 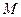 генеральной и генеральной и 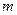 выборочной совокупностей, обладающих некоторым признаком выборочной совокупностей, обладающих некоторым признаком 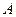 , к их объемам, называются соответственно генеральной , к их объемам, называются соответственно генеральной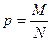 и выборочной долями и выборочной долями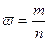 . .
В случае бесконечной генеральной совокупности (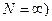 под генеральной средней и дисперсией понимаются соответственно математической ожидание под генеральной средней и дисперсией понимаются соответственно математической ожидание 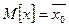 и дисперсия и дисперсия 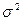 распределение признака распределение признака 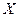 (генеральной совокупности), а под генеральной долей (генеральной совокупности), а под генеральной долей 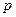 - вероятность данного события. - вероятность данного события.
Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности (по выборке) выносить суждение о свойствах генеральной совокупности в целом.
Чтобы по данным выборки можно было достоверно судить о генеральной совокупности, выборочная совокупность должна быть отобрана случайно
(т.е. по схеме случая или «урн»). При случайном отборе используют два способа образования выборки:
· Повторный отбор
, когда каждый элемент, отобранный и обследованный, возвращается в общую совокупность и может быть повторно отобран;
· Бесповторный отбор
, когда отобранный элемент не возвращается в общую совокупность.
Оценкой 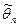 неизвестного параметра генеральной совокупности
неизвестного параметра генеральной совокупности 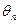 называют всякую функцию результатов наблюдений над случайной величиной называют всякую функцию результатов наблюдений над случайной величиной 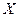 , с помощью которой судят о значении параметра , с помощью которой судят о значении параметра 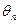 . Оценка . Оценка 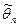 в отличие от оцениваемого параметра
в отличие от оцениваемого параметра 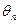 является случайной
величиной, зависящей от закона распределения является случайной
величиной, зависящей от закона распределения 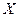 и числа и числа 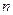 (объема выборки). (объема выборки).
В качестве оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности
, состоятельности
и эффективности
.
Оценка 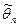 параметра параметра 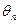 называется несмещенной
, если ее математическое ожидание равно оцениваемому параметру: называется несмещенной
, если ее математическое ожидание равно оцениваемому параметру:
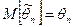
Требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.
Оценка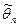 параметра
параметра 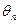 называется состоятельной
, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру: называется состоятельной
, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:
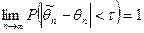 или или 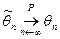 . .
Оценка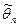 параметра параметра 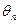 называется эффективной
, если она имеет наименьшую дисперсию среди всех возможных оценок параметра называется эффективной
, если она имеет наименьшую дисперсию среди всех возможных оценок параметра 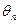 , вычисленных по выборкам одного и того же объема , вычисленных по выборкам одного и того же объема 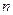 . .
Оценки 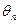 можно находить методами моментов, максимального правдоподобия
и наименьших квадратов. можно находить методами моментов, максимального правдоподобия
и наименьших квадратов.
Согласно методу моментов,
определенное количество выборочных моментов (начальных 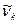 или центральный или центральный 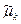 ) приравнивается к соответствующим теоретическим моментам распределения ( ) приравнивается к соответствующим теоретическим моментам распределения (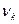 и и 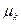 ) случайной величины ) случайной величины 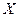 . .
Основы метода наибольшего правдоподобия
составляют функции правдоподобия,
выражающая плотность вероятности совместного появления результатов выборки 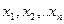 : :
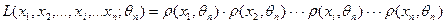 . .
Согласно метода наибольшего правдоподобия в качестве оценки неизвестного параметра 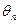 принимается такое значение принимается такое значение 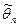 , которое максимизирует функцию , которое максимизирует функцию 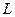 : :
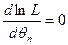 или или 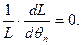
Метод наименьших квадратов
предусматривает определение оценки из условий минимизации квадратов отклонений выборочных данных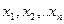 от определяемой оценки от определяемой оценки 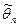 : :
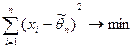 . .
Точечная и интервальная оценка.
Оценка неизвестного параметра 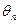 генеральной совокупности одним
числом генеральной совокупности одним
числом 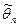 называют точечной
: называют точечной
:  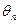 = =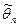 . .
Выборочная доля 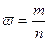 является несмещенной и состоятельной оценкой генеральной доли
является несмещенной и состоятельной оценкой генеральной доли  , дисперсия которой для повторной выборки равна: , дисперсия которой для повторной выборки равна:
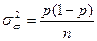 , ,
а для бесповторной:
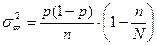
Выборочная средняя 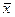 есть несмещенная и состоятельная оценка генеральной средней есть несмещенная и состоятельная оценка генеральной средней 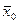 , дисперсия которой для повторной выборки рана: , дисперсия которой для повторной выборки рана:
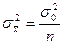 , ,
а для бесповторной:
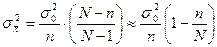 . .
Выборочная дисперсия 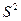 повторной и бесповторной выборок есть смещенная и состоятельная оценка генеральной дисперсии
повторной и бесповторной выборок есть смещенная и состоятельная оценка генеральной дисперсии 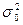 , так как , так как
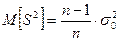 . .
Не смещенной и состоятельной оценкой генеральной дисперсии 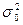 является исправленная выборочная дисперсия является исправленная выборочная дисперсия
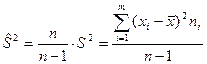 . .
Интервальной
оценкой параметра 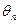 называется числовой интервал называется числовой интервал 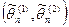 , который с заданной вероятностью , который с заданной вероятностью 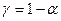 накрывает неизвестной значение параметра накрывает неизвестной значение параметра 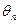 . Такой интервал называют доверительным
, а вероятность . Такой интервал называют доверительным
, а вероятность 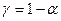 - доверительной вероятностью
или надежностью оценки. - доверительной вероятностью
или надежностью оценки.
Наиболее часто доверительный интервал выбирают симметричным относительно параметра 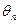 : :
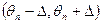 , ,
где 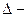 наибольшее отклонение оценки наибольшее отклонение оценки 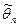 от параметра генеральной совокупности от параметра генеральной совокупности 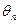 , возможное с вероятностью , возможное с вероятностью 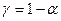 и называется предельной ошибкой выборки. и называется предельной ошибкой выборки.
При заданной доверительной вероятности 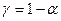 и большом объемы выборке, ее предельная ошибка оценки генеральной средней и генеральной доли равна и большом объемы выборке, ее предельная ошибка оценки генеральной средней и генеральной доли равна 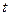 -кратной величине средней квадратической ошибки или средним квадратическим отклонениям выборочной средней -кратной величине средней квадратической ошибки или средним квадратическим отклонениям выборочной средней 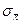 и выборочной доли и выборочной доли 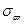 : :
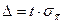 и и 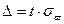 , , 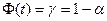 , ,
где 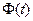 -функция (интеграл вероятностей) Лапласа. -функция (интеграл вероятностей) Лапласа.
Интервальные оценки (доверительные интервалы) для генеральной средней и генеральной доли равны:
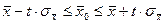 ; ;
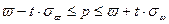 , ,
где 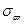 и и 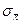 в зависимости от типа отбора (повторный или бесповторный) определяем по формулам: в зависимости от типа отбора (повторный или бесповторный) определяем по формулам:
· Для повторного отбора:
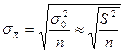 и и 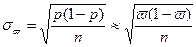 ; ;
· Для бесповторного отбора:
 и и 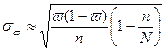 . .
Предельные ошибки и необходимый объем выборки (Повторный и бесповторный отбор)
Для определения необходимого объема выборки 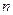 необходимо задать надежность (доверительную вероятность) необходимо задать надежность (доверительную вероятность) 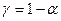 оценки и точность (предельную ошибку выборки) оценки и точность (предельную ошибку выборки) 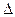 . В этом случае необходимый объем выборки для оценки генеральной средней . В этом случае необходимый объем выборки для оценки генеральной средней 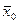 для повторного отбора находим по формуле: для повторного отбора находим по формуле:
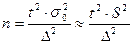 , ,
и для бесповторного отбора:
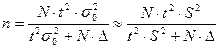 . .
Необходимый объем выборки для оценки генеральной доли 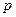 для повторного отбора находим: для повторного отбора находим:
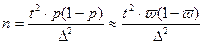 , ,
И для бесповторного отбора:
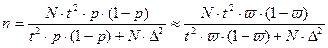 . .
Лекция №12. Проверка статистических гипотез.
Статистической гипотезой
называется любое предположение о виде или параметрах генеральной совокупности, проверяемое по выборке.
Различают простую
и сложную
статистические гипотезы. Простая гипотеза, в отличие от сложной, полностью определяет теоретическую функцию распределения наблюдаемой случайной величины.
Проверяемую гипотезу обычно называют нулевой  .
Наряду с нулевой гипотезой .
Наряду с нулевой гипотезой  рассматривают альтернативную,
или конкурирующую,
гипотезу
рассматривают альтернативную,
или конкурирующую,
гипотезу 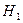 , являющуюся логическим отрицанием , являющуюся логическим отрицанием  . .
Правило, по которому принимается или отвергается  ,
называется статистическим критерием. ,
называется статистическим критерием.
Суть проверки статистической гипотезы заключается в том, что используется специальная составленная выборочная характеристика (критерий) 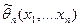 , полученная по выборке , полученная по выборке 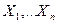 , точный или приближенный закон распределения которой при выдвинутой гипотезе , точный или приближенный закон распределения которой при выдвинутой гипотезе известно. По этому распределению определяется критическое значение критерия
известно. По этому распределению определяется критическое значение критерия 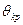 из условия, что вероятность из условия, что вероятность 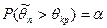 мала. Так что в соответствие с принципом практической уверенности в условиях данного исследования при правильности гипотезы мала. Так что в соответствие с принципом практической уверенности в условиях данного исследования при правильности гипотезы  событие
событие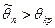 практически невозможно. Таким образом, множества значений критерия практически невозможно. Таким образом, множества значений критерия 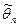 разбивается значением разбивается значением 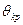 на два непересекающихся подмножества: на два непересекающихся подмножества:
· Область допустимых значений 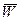 (область принятия гипотезы (область принятия гипотезы  ,
когда ,
когда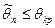 );
);
· Критическая область 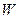 (область отбрасывания гипотезы (область отбрасывания гипотезы  , когда
, когда 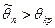 ).
).
При таком подходе возможны четыре случая (см. табл.):
Гипотеза 
|
Принимается
|
Отвергается |
| Верна |
Правильное решение |
Ошибка 1-го рода |
| Неверна |
Ошибка 2-го рода |
Правильное решение |
Таким образом, вероятность 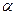 , называемая уровнем значимости
критерия, есть вероятность допущения ошибки 1-ого рода. , называемая уровнем значимости
критерия, есть вероятность допущения ошибки 1-ого рода.
Вероятность допустить ошибку 2-ого рода обозначают 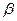 . Вероятность недопущения ошибки 2-ого рода . Вероятность недопущения ошибки 2-ого рода 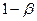 называется мощностью критерия. называется мощностью критерия.
При фиксированном объеме выборке невозможно одновременное уменьшение ошибок 1-ого и 2-ого рода. Критическая область 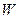 следует выбирать так, чтобы при заданном уроне значимости следует выбирать так, чтобы при заданном уроне значимости 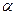 мощность критерия мощность критерия 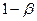 была максимальной. Вид критической области зависит от конкурирующей гипотезы была максимальной. Вид критической области зависит от конкурирующей гипотезы 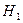 и бывает трех видом: и бывает трех видом:
· Правосторонняя, выбирается из соотношения: 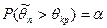 ; ;
· Левосторонняя: 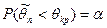 ; ;
· Двухсторонняя: 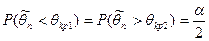 . .
Критерии проверки гипотез называю параметрическими, если известен закон распределения генеральной совокупности, что задает определенное распределение критерия. При неизвестном законе распределения генеральной совокупности, то критерии называют непараметрическими.
По своему прикладному содержанию. Статистические гипотезы подразделяются на несколько основных типов:
· О равенстве числовых характеристики генеральных совокупностей;
· О числовых значениях параметров;
· О законе распределения;
· Об однородности выборок (т.е. о принадлежности их одной и той же генеральной совокупности).
Проверка гипотез о равенстве средних значений при известной и неизвестной дисперсии.
Имеются две генеральные совокупности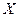 и и  с известными
дисперсиями с известными
дисперсиями  и и 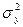 . Необходимо проверит гипотезу . Необходимо проверит гипотезу  о равенстве генеральных средних, т.е.
о равенстве генеральных средних, т.е.  :
: 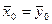 . Для проверки этой гипотезы взяты две независимые выборки объемами . Для проверки этой гипотезы взяты две независимые выборки объемами 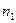 и и 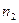 , по которым найдены средние арифметические , по которым найдены средние арифметические 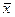 и и 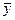 . В качестве критерия принимаем нормированную разность между . В качестве критерия принимаем нормированную разность между 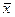 и и 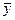 : :
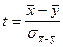 . .
Поскольку 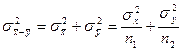 , то критерий при известных генеральных дисперсиях будет равен: , то критерий при известных генеральных дисперсиях будет равен:
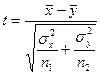
При выполнении гипотезы  критерий
критерий 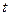 при больших объемах выборок или при малых, при условии, что генеральные совокупности при больших объемах выборок или при малых, при условии, что генеральные совокупности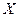 и и  подчиняются нормальному закону, так же будет подчиняться нормальному закону подчиняются нормальному закону, так же будет подчиняться нормальному закону 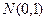 с нулевым математическим ожиданием и единичной дисперсией. Поэтому, например, при конкурирующей гипотезе с нулевым математическим ожиданием и единичной дисперсией. Поэтому, например, при конкурирующей гипотезе 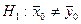 , выбирают двухстороннюю критическую область. Критическое значение критерия , выбирают двухстороннюю критическую область. Критическое значение критерия 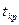 выбираем из условия: выбираем из условия:
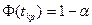 . .
Если фактически наблюдаемое значение критерия 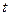 по абсолютному значению больше критического по абсолютному значению больше критического 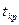 , определенного на уровне значимости , определенного на уровне значимости 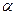 , т.е. , т.е. 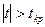 , то гипотеза , то гипотеза  отвергается. отвергается.
Если 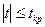 , то делаем вывод, что нулевая гипотеза , то делаем вывод, что нулевая гипотеза  не противоречит имеющимся наблюдениям.
не противоречит имеющимся наблюдениям.
При неизвестных
генеральных дисперсиях  и и 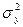 , но они равны, т.е. , но они равны, т.е. 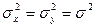 , то в качестве неизвестной величины , то в качестве неизвестной величины 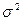 можно взять ее оценку – «исправленную» выборочную дисперсию: можно взять ее оценку – «исправленную» выборочную дисперсию:
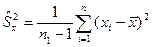 или или  . .
Однако лучшей оценкой дисперсии разности независимых выборочных средних 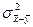 будет дисперсия смешанной совокупности будет дисперсия смешанной совокупности 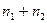 : :
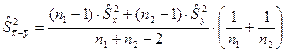 . .
В этом случае критерий вычисляем по выражению:
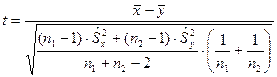 . .
Доказано, что в случае критерий 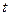 имеет распределение Стьюдента с имеет распределение Стьюдента с 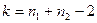 степенями свободы. Поэтому критическое значение критерия степенями свободы. Поэтому критическое значение критерия 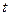 находится в зависимости от типа критической области по функции находится в зависимости от типа критической области по функции 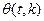 распределения Стьюдента, т.е. распределения Стьюдента, т.е. 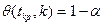 . .
При этом сохраняется тоже правило принятия гипотезы: гипотеза  отвергается на уровне значимости
отвергается на уровне значимости 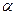 , если , если 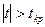 и принимается, если и принимается, если 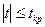 , т.е. с надежностью , т.е. с надежностью 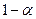 можно считать расхождение средних значений незначимым. можно считать расхождение средних значений незначимым.
В случае невозможности наложения допущения о равенстве генеральных дисперсий задача не имеет точного решения (пока) – это проблема Беренса-Фишера.
Рассмотренные критерии можно применять для исключения грубых ошибок при проведении наблюдений.
Например, если в ряде наблюдений 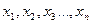 , , 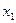 - резко отличается, то справедливость гипотезы - резко отличается, то справедливость гипотезы  :
: 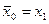 о принадлежности о принадлежности 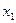 к остальным наблюдениям проверяем по критерию: к остальным наблюдениям проверяем по критерию:
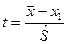 , ,
где 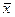 - средняя арифметическая, - средняя арифметическая, 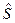 -«исправленное» среднее квадратическое отклонении ряда наблюдений -«исправленное» среднее квадратическое отклонении ряда наблюдений 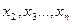 . При справедливости . При справедливости  критерий должен подчиняться так же закону распределения Стьюдента со степенью свободы
критерий должен подчиняться так же закону распределения Стьюдента со степенью свободы 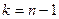 . При конкурирующей гипотезе . При конкурирующей гипотезе 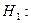 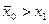 или или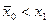 , т.е. является ли резко выделяющееся значение меньше или больше остальных наблюдений , т.е. является ли резко выделяющееся значение меньше или больше остальных наблюдений 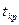 находится по функции находится по функции 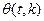 распределения Стьюдента при условии, что распределения Стьюдента при условии, что 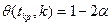 . Если . Если 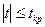 , то гипотеза , то гипотеза  принимается. При условии
принимается. При условии 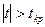 , гипотеза , гипотеза  отвергается.
отвергается.
Проверка гипотезы о равенстве дисперсий двух нормальных генеральных совокупностей.
Проверка гипотезы  , о том, что дисперсии двух нормально распределенных генеральных совокупностей
, о том, что дисперсии двух нормально распределенных генеральных совокупностей 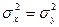 , сводится к сравнению выборочных «исправленных» дисперсий , сводится к сравнению выборочных «исправленных» дисперсий 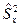 и и 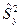 , вычисляемые по двум независимым выборкам объемом , вычисляемые по двум независимым выборкам объемом 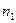 и и 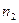 . В качестве критерия принимается отношение выборочных «исправленных» дисперсий . В качестве критерия принимается отношение выборочных «исправленных» дисперсий 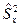 и и 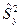 : :
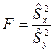 . .
Доказано, что при справедливости гипотезы  критерий
критерий 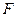 представляет собой случайную величину с распределением Фишера-Снедекора с степенями свободы представляет собой случайную величину с распределением Фишера-Снедекора с степенями свободы 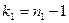 и и 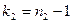 . .
Поэтому, выбрав необходимый уровень значимости 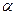 по таблицам распределения Фишера-Снедекора, находим критическое значение по таблицам распределения Фишера-Снедекора, находим критическое значение 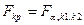 . .
Если 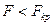 , то гипотеза , то гипотеза  принимается.
принимается.
Лекция№13.Проверка статистических гипотез о законе распределения генеральной совокупности
Проверку гипотезы  , о том, что генеральная совокупность подчиняется определенному теоретическому закону распределения
, о том, что генеральная совокупность подчиняется определенному теоретическому закону распределения 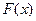 , осуществляют с помощью критериев согласия. Доля проверки гипотезы , осуществляют с помощью критериев согласия. Доля проверки гипотезы  выбирают некоторую случайную величину
выбирают некоторую случайную величину 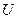 , характеризующую степень расхождения теоретического , характеризующую степень расхождения теоретического 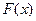 и эмпирического и эмпирического 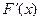 распределения, закон распределения которой при достаточно больших объемах выборки распределения, закон распределения которой при достаточно больших объемах выборки 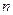 известен и практически не зависит от закона распределения генеральной совокупности. Зная закон распределения известен и практически не зависит от закона распределения генеральной совокупности. Зная закон распределения 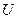 , можно найти вероятность того, что , можно найти вероятность того, что 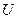 приняла значение не меньше, чем фактически наблюдаемое в опыте приняла значение не меньше, чем фактически наблюдаемое в опыте 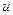 , т.е. , т.е. 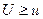 . Если . Если 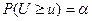 мала, то это означает в соответствии с принципом практической уверенности, что такие, как в опыте, и большие отклонения практически невозможны. В этом случае гипотезу мала, то это означает в соответствии с принципом практической уверенности, что такие, как в опыте, и большие отклонения практически невозможны. В этом случае гипотезу  отвергают. Если же вероятность
отвергают. Если же вероятность 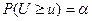 не мала, расхождение между эмпирическим и теоретическим распределением несущественно и гипотезу не мала, расхождение между эмпирическим и теоретическим распределением несущественно и гипотезу  можно считать правдоподобной или, по крайней мере, не противоречащей опытным данным.
можно считать правдоподобной или, по крайней мере, не противоречащей опытным данным.
Существует несколько критериев согласия: 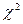 (хи- квадрат) Пирсона, Колмогорова, Смирнова и т.д. (хи- квадрат) Пирсона, Колмогорова, Смирнова и т.д.
Критерий согласия 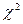 (хи- квадрат) Пирсона (хи- квадрат) Пирсона
В наиболее часто используемом на практике критерии 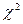 - Пирсона
в качестве меры расхождения
- Пирсона
в качестве меры расхождения 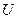 берется величина берется величина 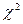 , равная относительной сумме квадратов отклонений межу эмпирическими
, равная относительной сумме квадратов отклонений межу эмпирическими 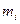 и теоретическими и теоретическими 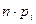 частотами попадания в интервалы частотами попадания в интервалы 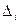 : :
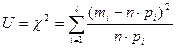 , ,
где 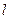 -число интервалов -число интервалов 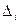 эмпирического распределения (вариационного ряда), эмпирического распределения (вариационного ряда), 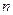 - объем выборки, - объем выборки, 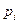 - вероятность попадания случайной величины в интервал - вероятность попадания случайной величины в интервал 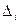 , вычисленная по закону распределения, соответствующему гипотезе , вычисленная по закону распределения, соответствующему гипотезе  . .
Доказано, что при справедливости гипотезы  и при
и при 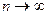 критерий критерий 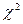 имеет
имеет 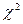 -
распределение со -
распределение со 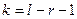 степенями свободы, где степенями свободы, где  - число параметров теоретического распределения, вычисленных по экспериментальным данным. - число параметров теоретического распределения, вычисленных по экспериментальным данным.
Методика применения критерия 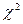 следующая:
следующая:
1. Разбиваем всю область наблюдаемых выборочных значений 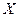 на на 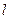 интервалов шириной интервалов шириной 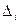 и подсчитываем количество выборочных значений и подсчитываем количество выборочных значений 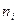 , попавших в каждый из этих интервалов. Предполагая, согласно выдвинутой гипотезы, известным теоретический закон распределения , попавших в каждый из этих интервалов. Предполагая, согласно выдвинутой гипотезы, известным теоретический закон распределения 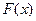 генеральной совокупности определяем генеральной совокупности определяем 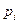 вероятность попадания случайной величины в интервал вероятность попадания случайной величины в интервал 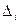 : :
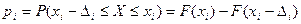 . .
Умножив полученные вероятности на объем выборки 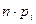 , получаем теоретические частоты попадания в интервалы и рассчитываем меру расхождения между частотами , получаем теоретические частоты попадания в интервалы и рассчитываем меру расхождения между частотами 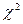 . .
2.Для выбранного уровня значимости 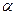 по таблице по таблице 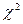 - распределения находим критическое значение
- распределения находим критическое значение 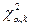 при числе степеней свободы при числе степеней свободы 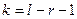 . .
3. Если фактически наблюдаемое значение 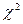 больше критического, т.е.
больше критического, т.е. 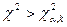 , то гипотеза , то гипотеза  отвергается, если
отвергается, если 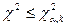 , гипотеза , гипотеза  не противоречит опытным данным.
не противоречит опытным данным.
Следует отметить, что критерий 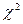 имеет закон распределения
имеет закон распределения 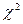 лишь при
лишь при 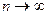 . Поэтому этот критерий нельзя применять при малых объемах выборок. Поэтому необходимо чтобы в каждом интервале было не менее 5-10 выборочных значений, а весь объем выборки был порядка сотен. . Поэтому этот критерий нельзя применять при малых объемах выборок. Поэтому необходимо чтобы в каждом интервале было не менее 5-10 выборочных значений, а весь объем выборки был порядка сотен.
Критерий согласия Колмогорова
Критерий Колмогорова применяется в тех случаях, когда заранее известен не только вид распределения, но и числовые характеристики распределения. В этом критерии в качестве меры расхождения между теоретическими и эмпирическими распределениями рассматривают максимальное значение абсолютной величины разности между эмпирической функцией распределения 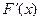 и соответствующей теоретической функции распределения и соответствующей теоретической функции распределения 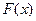 : :
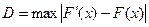 , ,
называемое статистикой критерия Колмогорова.
Доказано, что какова бы ни была функция распределения  , при неограниченном увеличении числа наблюдений , при неограниченном увеличении числа наблюдений 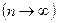 вероятность неравенства вероятность неравенства 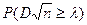 стремится к пределу стремится к пределу
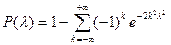 . .
Задавая уровень значимости 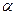 , из соотношения , из соотношения 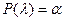 по приведенной формуле рассчитаны и представлены в таблицах критические значения по приведенной формуле рассчитаны и представлены в таблицах критические значения 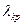 . Так, например, уровням значимости . Так, например, уровням значимости  , равным 0,05, 0,01 и 0,001 соответствуют , равным 0,05, 0,01 и 0,001 соответствуют  равные 1,36, 1,63 и 1,95 соответственно. равные 1,36, 1,63 и 1,95 соответственно.
Методика применения критерия Колмогорова следующая:
- Строятся эмпирическая функция распределения
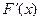 и предполагаемая теоретическая функция распределения и предполагаемая теоретическая функция распределения 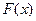 . .
- Определяется мера расхождения между теоретическим и эмпирическим распределением
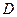 и вычисляется величина : и вычисляется величина :
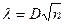
При заданном уровне значимости 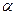 , сравнивается вычисленное значение , сравнивается вычисленное значение 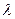 с критическим с критическим 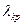 . Если . Если 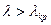 , то гипотеза , то гипотеза  отвергается. Если
отвергается. Если 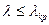 , то считают, что гипотеза , то считают, что гипотеза  не противоречит опытным данным.
не противоречит опытным данным.
Следует отметить, что на практике часто не известны параметры законов распределения генеральных совокупностей. Использование в этом случае критерий Колмогорова, заменяя неизвестные характеристики оценками, дает завышенное значение вероятности 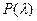 и, соответственно, критическое значение и, соответственно, критическое значение 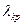 , что повышает вероятность ошибки 2-ого рода. Поэтому в этих случаях критерий Колмогорова можно использовать как предварительную оценку: , что повышает вероятность ошибки 2-ого рода. Поэтому в этих случаях критерий Колмогорова можно использовать как предварительную оценку:
- Если гипотеза не удовлетворяет условиям критерия Колмогорова, то ее можно отбросить;
- Если же гипотеза по критерию Колмогорова не противоречит опытным данным, то необходима дополнительная проверка другими критериями, например,
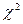 - Пирсона.
- Пирсона.
Лекция №14. Основные понятия дисперсионного анализа
Дисперсионный анализ
– статистический метод оценки влияния различных факторов на результаты эксперимента. Суть анализа заключается в разложении общей вариации случайной величины на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействие. Факторами обычно называют внешние условия, влияющие на эксперимент.
По числу факторов, влияние которых исследуется, различают:
· Однофакторный дисперсионный анализ;
· Двухфакторный дисперсионный анализ;
· Многофакторный дисперсионный анализ.
Для проведения дисперсионного анализа необходимо соблюдение следующих условий: результаты наблюдений должны быть независимыми случайными величинами с нормальным законом распределения с одинаковой дисперсией.
Однофакторный дисперсионный анализ
Однофакторная дисперсионная модель имеет вид:
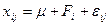 , ,
Где 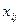 -значение исследуемой переменной, полученной на -значение исследуемой переменной, полученной на 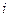 -м уровне фактора ( -м уровне фактора (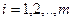 ) с ) с 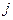 -м порядковым номером ( -м порядковым номером (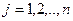 ); );
 - общая средняя; - общая средняя;
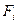 - эффект, обусловленный влиянием - эффект, обусловленный влиянием 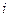 -го уровня фактора, т.е. вариация переменной между отдельными уровнями фактора; -го уровня фактора, т.е. вариация переменной между отдельными уровнями фактора;
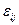 -случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариация переменной внутри отдельного уровня фактора. -случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариация переменной внутри отдельного уровня фактора.
Под уровнем фактора
понимается некоторая его мера или состояние, например номер партии детали, количество вносимых удобрений и т.п.
Проверим существенность влияния № партий изделий на их качество. Пусть имеется 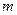 партий изделий. Из каждой партии отобрано соответственно партий изделий. Из каждой партии отобрано соответственно 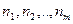 изделий (положим, что изделий (положим, что 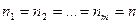 ). Значения показателей качества этих изделий представим в виде матрицы (или таблицы): ). Значения показателей качества этих изделий представим в виде матрицы (или таблицы):
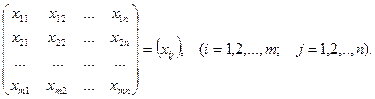
Если полагать, что элементы строк матрицы наблюдений – это численные значения (реализации) случайных величин  , выражающих качество изделий и имеющих нормальный закон распределения с математическим ожиданием соответственно , выражающих качество изделий и имеющих нормальный закон распределения с математическим ожиданием соответственно  и одинаковыми дисперсиями и одинаковыми дисперсиями  , то данная задача сводится к проверке нулевой гипотезы , то данная задача сводится к проверке нулевой гипотезы  : : 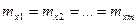 . .
Предположим, что для каждой  -ой партии( -ой партии( -го уровня фактора) из -го уровня фактора) из  изделий имеем средний показатель качества изделий имеем средний показатель качества 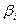 , равный сумме общего среднего , равный сумме общего среднего 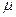 и ее вариации и ее вариации 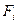 , обусловленной , обусловленной 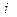 -ым уровнем фактора: -ым уровнем фактора:
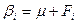 , ,
называемая группой средней для 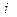 -го уровня фактора. -го уровня фактора.
Очевидно, что оценкой 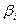 является средняя арифметическая является средняя арифметическая 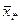 из из 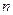 изделий изделий 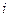 -ой партии ( -ой партии (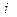 -го уровня фактора): -го уровня фактора):
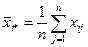 . .
Оценкой общего среднего 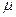 является средняя арифметическая всей совокупности показателей качества: является средняя арифметическая всей совокупности показателей качества:
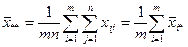 . .
Рассмотрим сумму квадратов отклонений  от общей средней от общей средней  в виде : в виде :
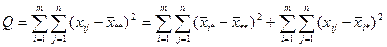
Или 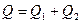 : :
где 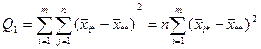 - сумма квадратов отклонений групповых средних от общей средней, или межгрупповая
(факторная) сумма квадратов отклонений; - сумма квадратов отклонений групповых средних от общей средней, или межгрупповая
(факторная) сумма квадратов отклонений;
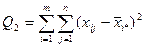 - сумма квадратов отклонений наблюдений от групповых средних, или внутригрупповая (остаточная) сумма квадратов отклонений. - сумма квадратов отклонений наблюдений от групповых средних, или внутригрупповая (остаточная) сумма квадратов отклонений.
В разложении общей суммы квадратов отклонений 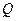 заключенная основная идея дисперсионного анализа: общая вариация показателя качества, измеренная суммой заключенная основная идея дисперсионного анализа: общая вариация показателя качества, измеренная суммой  , складывается из двух компонент - , складывается из двух компонент -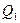 и и 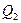 , характеризующих изменчивость этого показателя между партиями ( , характеризующих изменчивость этого показателя между партиями (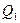 ) под воздействием изучаемого фактора и изменчивость «внутри» партий ( ) под воздействием изучаемого фактора и изменчивость «внутри» партий (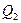 ) под воздействием всех других неучтенных факторов. В дисперсионном анализе изменчивость показателя оценивается не по суммам квадратов отклонений, а по выборочным дисперсиям ) под воздействием всех других неучтенных факторов. В дисперсионном анализе изменчивость показателя оценивается не по суммам квадратов отклонений, а по выборочным дисперсиям 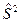 , которые являются несмещенными оценками соответствующих дисперсий генеральных совокупностей: , которые являются несмещенными оценками соответствующих дисперсий генеральных совокупностей:
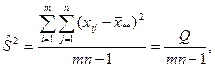
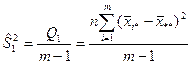 , ,
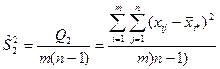 , ,
где 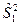 и и 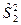 - получили название межгрупповой и внутригрупповой дисперсиями. - получили название межгрупповой и внутригрупповой дисперсиями.
Доказано, что, если влияние всех уровней фактора 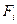 на показатели качества (для нашего примера) одинаково, то на показатели качества (для нашего примера) одинаково, то 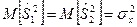 . Иными словами, межгрупповая и внутригрупповая дисперсии являются несмещенными оценками общей дисперсии генеральной совокупности и проверка нулевой гипотезы . Иными словами, межгрупповая и внутригрупповая дисперсии являются несмещенными оценками общей дисперсии генеральной совокупности и проверка нулевой гипотезы 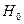 сводится к проверки сводится к проверки 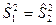 . Для этого вычисляется критерий (статистика): . Для этого вычисляется критерий (статистика):
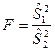 . .
При правильности нулевой гипотезы 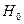 критерий критерий 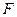 должен подчиняться закону распределения Фишера со степенями свободы должен подчиняться закону распределения Фишера со степенями свободы 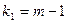 и и 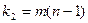 . Поэтому при заданном уровне значимости . Поэтому при заданном уровне значимости 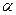 критическое значение критическое значение 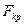 критерия находим по таблицам критерия находим по таблицам 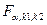 закона распределения Фишера. закона распределения Фишера.
Если 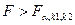 , то нулевая гипотеза отвергается и делается заключение о существенности влияния фактора , то нулевая гипотеза отвергается и делается заключение о существенности влияния фактора 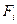 на случайную величину. на случайную величину.
При 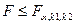 нет оснований отвергать гипотезу нет оснований отвергать гипотезу 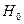 и считают, что влияние фактора несущественно. и считают, что влияние фактора несущественно.
Кроме того, по величине отношения 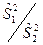 судят, насколько сильно проявляется влияние фактора. судят, насколько сильно проявляется влияние фактора.
Для упрощения расчетов сумм квадратов 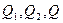 удобно пользоваться следующими формулами, которые позволяют предварительно не находить средние значения удобно пользоваться следующими формулами, которые позволяют предварительно не находить средние значения 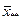 и и 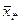 : :
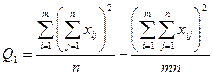 , , 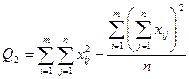 . .
Понятие о двухфакторном дисперсионном анализе
Двухфакторная дисперсионная модель имеет вид:
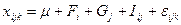 , ,
где 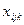 -значение наблюдений в ячейке -значение наблюдений в ячейке 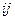 с номером с номером 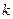 ; ;
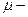 общая средняя; общая средняя;
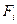 - эффект, обусловленный влиянием - эффект, обусловленный влиянием 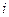 -го уровня фактора -го уровня фактора 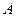 ; ;
 - эффект, обусловленный влияние - эффект, обусловленный влияние  -го уровня фактора -го уровня фактора 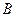 ; ;
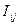 - эффект, обусловленный взаимодействием двух факторов - эффект, обусловленный взаимодействием двух факторов 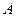 и и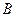 ; ;
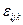 - случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариация переменной внутри отдельных уровней факторов. - случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариация переменной внутри отдельных уровней факторов.
Например, в условиях предыдущей задачи о качестве различных 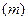 партий изделия изготавливались на различных партий изделия изготавливались на различных  станках и требуется выяснить, имеются ли существенные различия в качестве изделий по каждому фактору: станках и требуется выяснить, имеются ли существенные различия в качестве изделий по каждому фактору:
·  - партия изделия; - партия изделия;
· 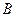 - станок. - станок.
Все имеющиеся данные представим в виде таблицы, в которой по строкам – уровни 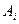 фактора фактора 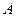 , по столбцам – уровни , по столбцам – уровни 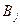 фактора фактора 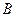 , а в соответствующих клетках, или ячейках, таблицы находятся значения показателей качества изделий , а в соответствующих клетках, или ячейках, таблицы находятся значения показателей качества изделий 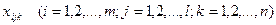 : :
Групповые средние находятся по формулам:
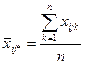 , ,
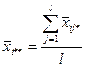 , ,
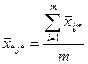 . .
Общая средняя:
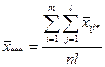
Далее рассчитываются 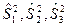 - межгрупповые дисперсии по фактору - межгрупповые дисперсии по фактору 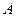 , по фактору , по фактору 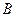 и по их взаимодействию, а так же и по их взаимодействию, а так же 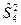 - остаточную дисперсию (внутригрупповую): - остаточную дисперсию (внутригрупповую):
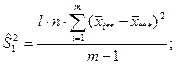 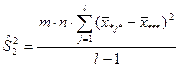 ; ;
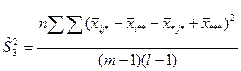 ; ; 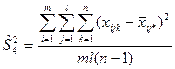 . .
Для оценки влияния факторов  и их взаимодействия на случайную величину рассчитывают три критерия: и их взаимодействия на случайную величину рассчитывают три критерия:
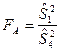 ; ; 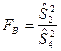 ; ; 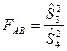
и сравнивают эти значения с соответствующим критическим значением, определяемым, при заданном уровне значимости 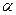 , по табличным значениям закона распределения Фишера. , по табличным значениям закона распределения Фишера.
Автоматизированный дисперсионный анализ возможен с помощью табличного процессора Excel.Для этого в опции Сервис находим пакет анализа данных (см. рис.)
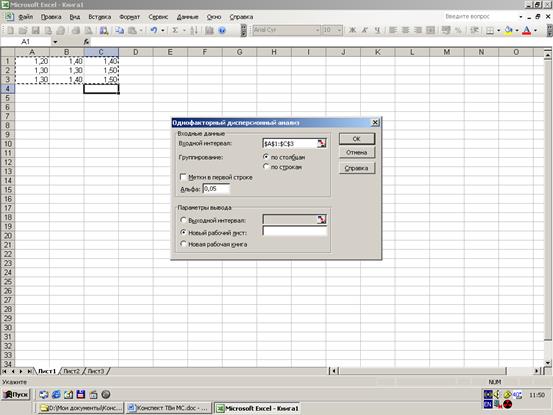
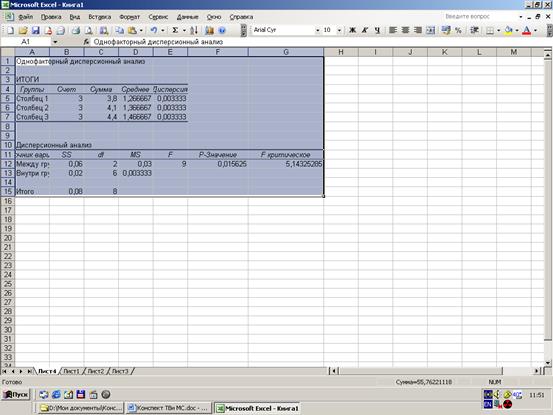
Лекция№15. Корреляционно – регрессионный анализ
В естественных науках различают функциональную и статистическую зависимости. Под функциональной понимают такую зависимость, когда значению одной переменной соответствует вполне определенное значение другой переменной. Под статистической (вероятностной или стохастической) понимают такую зависимость, когда одна переменная влияет на закон распределения другой. Наибольший интерес для практики представляют вероятностные зависимости в виде закономерностей изменения средних значений (условного математического ожидания) одной случайной величины при условии, что другая принимает определенные значения. Такие вероятностные зависимости получили название корреляционных. Корреляционной
зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.
Простейшая корреляционная зависимость может быть представлена в виде уравнения регрессии:
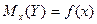 или или 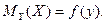
Для отыскания такого уравнения регрессии, строго говоря, необходимо знать закон распределения двумерной случайной величины 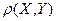 . В теории вероятностей, например, для двумерного нормального закона плотность совместного распределения двух переменных . В теории вероятностей, например, для двумерного нормального закона плотность совместного распределения двух переменных 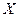 и и 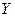 имеет вид: имеет вид:
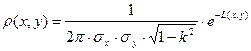 , ,
где 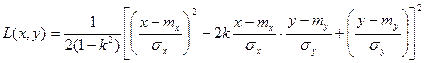 ; ;
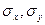 - дисперсии переменных - дисперсии переменных 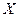 и и 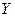 ; ;
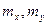 - математические ожидания переменных - математические ожидания переменных 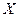 и и 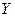 ; ;
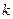 - коэффициент корреляции между переменными - коэффициент корреляции между переменными 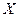 и и 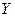 , определяемый через корреляционный момент (ковариацию) , определяемый через корреляционный момент (ковариацию) 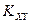 по формуле: по формуле:
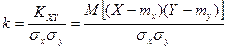 . .
Величина 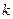 характеризует тесноту связи между случайными переменными характеризует тесноту связи между случайными переменными 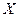 и и 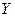 в генеральной совокупности
. Известно, что при совместном нормальном законе распределения случайных величин в генеральной совокупности
. Известно, что при совместном нормальном законе распределения случайных величин 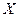 и и 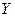 выражение для уловных математических ожиданий, т.е. уравнения регрессии, выражаются линейными функциями: выражение для уловных математических ожиданий, т.е. уравнения регрессии, выражаются линейными функциями:
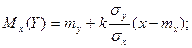
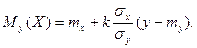
Из свойства коэффициента корреляции следует, что 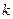 является показателем тесноты связи лишь в случае линейной зависимости (линейной регрессии) между переменными, получаемые, в частности, при совместном нормальном распределение.
является показателем тесноты связи лишь в случае линейной зависимости (линейной регрессии) между переменными, получаемые, в частности, при совместном нормальном распределение.
В практике статистических исследований нам не известны законы распределения генеральных совокупностей, располагаем лишь выборкой пар значений 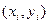 ограниченного объема. В этом случае речь может идти о нахождении приближенного выражения (выборочного) уравнения регрессии, являющейся наилучшей оценкой уравнения регрессии генеральной совокупности. И эта задача решается методами корреляционно-регрессионного анализа, основными задачами которых соответственно являются: ограниченного объема. В этом случае речь может идти о нахождении приближенного выражения (выборочного) уравнения регрессии, являющейся наилучшей оценкой уравнения регрессии генеральной совокупности. И эта задача решается методами корреляционно-регрессионного анализа, основными задачами которых соответственно являются:
- Выявление связи между случайными переменными и оценка ее тесноты;
- Установление формы и изучение зависимости между случайными переменными.
Основной метод нахождения неизвестных параметров уравнений регрессии в статистических исследованиях является метод наименьших квадратов
. Суть этого метода в том, что неизвестные параметры уравнений регрессии выбираются таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних 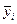 , вычисленных по наблюдаемым данным: , вычисленных по наблюдаемым данным:
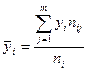 , ,
где 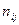 - частоты пар - частоты пар 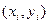 и и 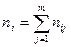 ; ;  - число интервалом по переменной - число интервалом по переменной 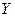 , от значений, найденных по уравнению регрессии , от значений, найденных по уравнению регрессии 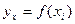 , была минимальной: , была минимальной:
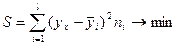 , ,
где 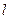 -число интервалов по переменной -число интервалов по переменной 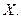

Линейная корреляционная зависимость и прямые регрессии
Линейную корреляционную зависимость между переменными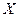 и и 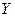 выражают в виде линейного уравнения регрессии: выражают в виде линейного уравнения регрессии:
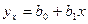 или или 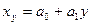 , ,
неизвестные параметры которых находим методом наименьших квадратов.
Например, для 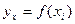 находим минимум находим минимум
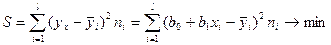
на основании необходимого условия экстремума функции двух переменных 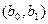 приравнивая нулю ее частные производные, т.е. приравнивая нулю ее частные производные, т.е.
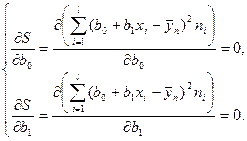
После преобразований получаем систему нормальных уравнений для определения параметров линейной регрессии:
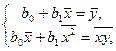
где соответствующие средние определяются по формулам:
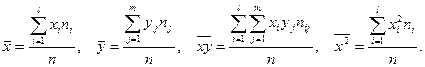
Подставляя значения 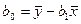 в уравнение регрессии в уравнение регрессии 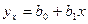 получаем: получаем:
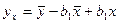 или или 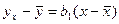 , ,
где коэффициент 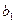 получил название коэффициента регрессии получил название коэффициента регрессии
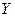 по по 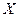 и обозначение и обозначение 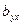 . Этот коэффициент показывает на сколько единиц в среднем изменяется переменная . Этот коэффициент показывает на сколько единиц в среднем изменяется переменная 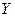 при увеличении переменной при увеличении переменной 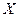 на одну единицу. на одну единицу.
Решая систему нормальных уравнений, найдем  : :
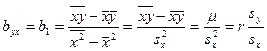 , ,
где  - выборочная дисперсия переменной - выборочная дисперсия переменной  : :
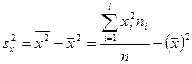 , ,
 - выборочный корреляционный момент или выборочная ковариация: - выборочный корреляционный момент или выборочная ковариация:
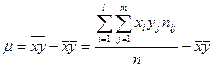 , ,

 - выборочный коэффициент корреляции: - выборочный коэффициент корреляции:
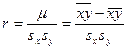 . .
Уравнение регрессии 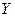 по по 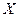 окончательно выглядит следующим образом: окончательно выглядит следующим образом:
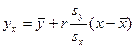 . .
Рассуждая аналогично находят уравнение регрессии 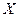 по по 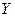 : :
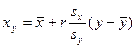 . .
Сравнение уравнения регрессии, полученные методом наименьших квадратов, с уравнением регрессии двумерной случайной величины с нормальным законом распределения показывает их идентичность. Поэтому для оценки линейного уравнения регрессии генеральных совокупностей 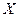 и и 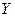 по выборке в формулах по выборке в формулах
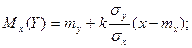
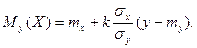
Необходимо заменить параметры 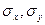 , ,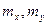 и и 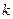 их состоятельными выборочными оценками – соответственно их состоятельными выборочными оценками – соответственно 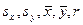 . .
Свойства выборочного (статистического) коэффициента корреляции
Для оценки тесноты связи между переменными 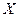 и и 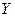 по выборочным значениям используют статистический коэффициент корреляции по выборочным значениям используют статистический коэффициент корреляции 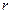 : :
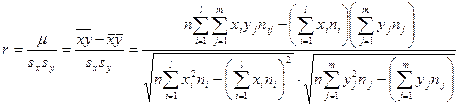 . .
Если данные не сгруппированы в виде корреляционной таблицы и представляют 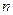 пар чисел пар чисел 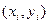 , то для вычисления коэффициента корреляции проводят по следующей формуле: , то для вычисления коэффициента корреляции проводят по следующей формуле:
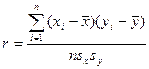 . .
Между коэффициентом корреляции 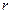 и коэффициентами регрессии и коэффициентами регрессии 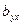 и и 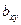 существует связь: существует связь: 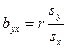 , , 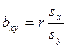 , , 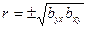 . .
Основные свойства коэффициента корреляции (при достаточно большом объеме выборке 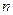 ): ):
1. Коэффициент корреляции лежит в пределах: 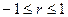 ; ;
2. Если все значения переменных увеличить (уменьшить) на одно и то же число или в одно и то же число раз, по величина коэффициента корреляции не изменится.
3. При 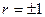 корреляционная связь представляет линейную функциональную зависимость. корреляционная связь представляет линейную функциональную зависимость.
4. При 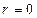 корреляционная линейная
связь отсутствует. корреляционная линейная
связь отсутствует.
При оценке тесноты связи между переменными 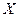 и и 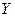 по выборочному коэффициенту корреляции необходимо проверить значимость этого коэффициента, т.е. установить достаточна ли его величина для обоснования вывода о наличии корреляционной связи. Для этого необходимо проверить нулевую гипотезу по выборочному коэффициенту корреляции необходимо проверить значимость этого коэффициента, т.е. установить достаточна ли его величина для обоснования вывода о наличии корреляционной связи. Для этого необходимо проверить нулевую гипотезу 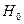 : : 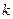 - коэффициент корреляции между генеральными совокупностями - коэффициент корреляции между генеральными совокупностями 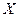 и и 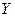 равен нулю. При справедливости этой гипотезы статистика (критерий) равен нулю. При справедливости этой гипотезы статистика (критерий)
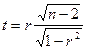
Имеет 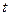 - распределение Стьюдента с - распределение Стьюдента с 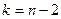 степенями свободы. При заданном уровне значимости степенями свободы. При заданном уровне значимости 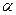 и степени свободы и степени свободы 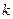 находим по таблицам закона распределения Стьюдента критическое значение находим по таблицам закона распределения Стьюдента критическое значение 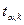 . Если . Если 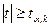 , то нулевая гипотеза об отсутствии корреляционной связи между переменными , то нулевая гипотеза об отсутствии корреляционной связи между переменными 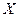 и и 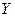 отвергается и переменные считаются зависимыми. При отвергается и переменные считаются зависимыми. При 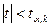 нет оснований отвергать нулевую гипотезу. Значимость коэффициента корреляции свидетельствует и о значимости коэффициентов регрессии, соответственно и о значимости линейного уравнения регрессии. нет оснований отвергать нулевую гипотезу. Значимость коэффициента корреляции свидетельствует и о значимости коэффициентов регрессии, соответственно и о значимости линейного уравнения регрессии.
Понятие о нелинейной регрессии, индекс корреляции и коэффициент детерминации
В экономических приложениях часто возникает необходимость выражать корреляционную зависимость в виде нелинейных уравнений регрессии, поскольку линейные зависимости приводят к большим ошибкам. Выбор вида нелинейной регрессии называется спецификацией
или этапом параметризации модели
и осуществляется методами визуального оценивания точек корреляционного поля, анализа сути наблюдаемых экономических процессов и т.п. Наиболее часто в экономических исследованиях используют следующие виды нелинейной регрессии:
· Полиноминальная 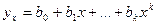 ; ;
· Гиперболическая 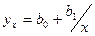 ; ;
· Степенное 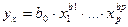 и т.п. и т.п.
Для определения неизвестных параметров выбранного уравнения регрессии используется метод наименьших квадратов
.
При нелинейной регрессии для оценки тесноты связи между переменными используют не коэффициент корреляции  , а индекс корреляции , а индекс корреляции 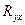 и коэффициент детерминации и коэффициент детерминации 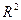 . .
Индекс корреляции 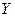 по по 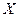 вычисляется по формуле: вычисляется по формуле:
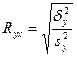 , ,
где 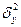 - межгрупповая дисперсия, выражающая ту часть вариации переменной - межгрупповая дисперсия, выражающая ту часть вариации переменной 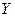 , которая обусловлена изменчивостью переменной , которая обусловлена изменчивостью переменной 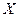 или регрессией и вычисляемая по формуле: или регрессией и вычисляемая по формуле:
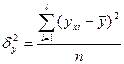 ; ;
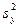 - общая дисперсия переменной: - общая дисперсия переменной:
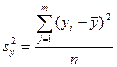
Коэффициент детерминации, равный квадрату индекса корреляции, показывает долю общей вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющей переменной:
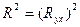 . .
Чем ближе 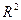 к единице, тем теснее наблюдения примыкают к линии регрессии, тем лучше регрессия описывает зависимость переменных. к единице, тем теснее наблюдения примыкают к линии регрессии, тем лучше регрессия описывает зависимость переменных.
При парной линейной регрессии индекс корреляции 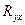 равен коэффициенту корреляции равен коэффициенту корреляции 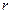 по абсолютному значению: по абсолютному значению: 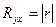 . .
Табличный процессор Excel так же позволяет проводит автоматизированный корреляционно- регрессионный анализ. Для этого в опции Сервис находим пакет анализа данных (см. рис.)
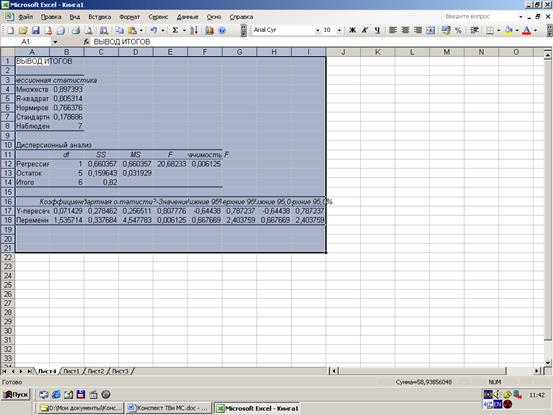
Литература
1. Мацкевич И.П., Свирид Г.П. Высшая математика. Теория вероятностей и математическая статистика. - Мн.: Высшая школа, 1993.
2. Лихолетов И.И., Мацкевич И.П. Руководство к решению задач по высшей математики с основами математической статистики и теории вероятностей. - Мн.: Высшая школа, 1976.
3. Булдык Г.М. Теория вероятностей и математическая статистика. - Мн.: Высшая школа, 1989.
4. Венцель Е.С. Теория вероятностей. - М.: Наука, 1969.
5. Кремер Н.Ш. Теория вероятностей и математическая статистика. - М.: ЮНИТИ-ДАНА,2000.-543 с.
6. Свирид Г.П.,Черторицкий Ю.Н.,Шевченко Л.И. Теория вероятностей и математическая статистика. Контрольные задания и методические рекомендации к ним для студентов экономических специальностей.-Мн.: БГЭУ,1998.
7. Булдык Г.М., Ковальчук В.М. Теория вероятностей и математическая статистика. Практикум. Часть 1.- Мн.: БГЭУ, 1999.-54 с.
8. Гороховик С.Я. Рыбалтовский И.В. Система случайных величин. Индивидуальные задания по теории вероятностей для студентов всех специальностей. – Мн.:БГЭУ,2000. – 18с.
|