Введение
Под лазерами на свободных электронах (ЛСЭ) обычно понимают устройства (приборы), в которых происходит усиление или генерация когерентного электромагнитного излучения с использованием явления стимулированного излучения релятивистских свободных электронов, совершающих наряду с поступательным также и колебательное движение в поле внешних сил. В качестве таких внешних сил могут выступать силы, действующие на электрон со стороны пространственно-периодических магнитного (магнитостатическая накачка) или электрического (электростатическая накачка) полей либо интенсивной электромагнитной волны, падающей на электронный пучок (электромагнитная накачка). Накачка первого типа имеет место в ондуляторах и убитронах, накачка второго типа может проявиться при каналировании электронов в кристаллах. Электромагнитная накачка может быть использована для преобразования мощного длинноволнового СВЧ-излучения в коротковолновое — инфракрасное и оптическое — при его рассеянии на релятивистском электронном пучке.
В понятие ЛСЭ нередко включают более широкий класс источников когерентного излучения, в которых используется индуцированное излучение релятивистских свободных электронов любой природы, в том числе черенковское, переходное, тормозное, магнитотормозное и т. д. Источники СВЧ-излучения на нерелятивистских электронных пучках, основанные на указанных механизмах (ЛБВ, ЛОВ, карсинотроны, гиротроны, магнетроны, клистроны и т. д.), уже получили широкое распространение и достаточно хорошо изучены, чего нельзя сказать о ЛСЭ.
Характерная особенность ЛСЭ, отличающая их от приборов классической электроники, заключается в том, что благодаря использованию релятивистских эффектов имеется возможность генерации коротковолнового излучения в макроскопических системах.
Вторая отличительная особенность ЛСЭ, выделяющая их также и среди других, уже хорошо разработанных, источников когерентного излучения (например: традиционных ОКГ на переходах дискретного спектра атомов и молекул) заключается в возможности плавной перестройки частоты в широком диапазоне с помощью изменения макроскопических параметров: энергии электронного пучка либо периода магнитного поля накачки.
Именно эти особенности делают ЛСЭ наиболее перспективными из всех известных источников когерентного излучения и обусловливают все возрастающий интерес к ним, наблюдающийся в последние годы.
Генерация СВЧ электронными потоками
Рассматривая физические основы квантовой электроники и принципы действия тех или иных конкретных лазеров, мы видели, что использование эффекта индуцированного излучения в системах с дискретными уровнями энергии (дискретными зонами энергии), т. е. в системах, существенно квантовых, позволило квантовой электронике единым методом генерации охватить огромный спектральный диапазон от радиоволн до вакуумного УФ излучения. Здесь необходимо подчеркнуть одно многозначительное обстоятельство. Несмотря на существование квантовых усилителей и генераторов (мазеров), генерация электромагнитных колебаний в радио- (СВЧ) диапазоне основывается, главным образом, на взаимодействии потоков свободных электронов с волноводными и резонаторными структурами, т. е. осуществляется классическими методами.
Реклама

Между тем эффект индуцированного излучения не является но своей природе принципиально квантовым и возможен в классических системах. Закономерен, следовательно, вопрос о возможности переноса электронных методов генерации из СВЧ в оптический диапазон. По аналогии с тем, что существенно квантовые системы способны генерировать колебания в диапазоне от СВЧ до вакуумного УФ, естественно ожидать, что индуцированное излучение таких классических объектов, как свободные электроны, тоже может быть применено для генерации электромагнитных колебаний в широком спектральном диапазоне от радио до световых волн.
В соответствии со смыслом слова лазер генератор электромагнитного излучения, использующий индуцированное испускание света электронными потоками, естественно называть лазером на свободных электронах или электронным лазером.
В классической вакуумной электронике СВЧ размеры генерирующих приборов или их характерных частей сравнимы с длиной волны генерируемого излучения. Область взаимодействии электронов с высокочастотным полем излучения, в которой кинетическая энергия электронов преобразуется в энергию поля излучения, представляет собой часть колебательной системы электродинамической резонаторной структуры, которая, как правило, обладает многими собственными частотами. Время пролета электронов через пространство взаимодействия или, что более характерно, время пролета между отдельными элементами резонансной структуры совпадает, по крайней мере, по порядку величины, с периодом колебаний генерируемого излучения.
Для всех генераторов вакуумной электроники СВЧ принципиально важным является обеспечение синхронизма между перемещением электронов и той электромагнитной волной, в которую перекачивается их энергия. В процессе взаимодействия электронов с высокочастотным полем волны в электронном потоке формируются сгустки частиц (фазовая группировка). Электронные сгустки по мере своего дальнейшего движения отдают энергию полю излучения, взаимодействуя с той его компонентой, для которой должным образом выполнено условие синхронизма.
Группировка электронов в сгустки характерна для всех приборов СВЧ, хотя ее конкретная реализация может происходить по-разному в разных приборах. Наиболее нагляден процесс группировки электронов в лампе бегущей волны, в которой используется длительное взаимодействие с полем волны электронного потока, распространяющегося прямолинейно вдоль направления распространения бегущей электромагнитной волны. При умеренных, т. е. существенно дорелятивистских, скоростях поступательного движения электронов синхронизм взаимодействия обеспечивается замедлением распространения волны. Простейшая замедляющая структура представляет собой однозаходную проволочную спираль. Вдоль витка спирали волна распространяется со скоростью, близкой к скорости света. В направлении оси спирали z фазовая скорость волны составляет примерно u z = cd/2 p а, где а — радиус спирали, d — ее шаг. Электроны, двигаясь вдоль оси синхронно с волной, группируются в сгустки под действием ускоряющих и тормозящих участков волны.
Реклама

Рис. 1 показывает простейший случай, когда продольная составляющая электрического поля бегущей волны записывается в виде Е z = Е 0 (w t- w z/ u z ,). На этом рисунке стрелками показаны силы, действующие на электроны. Видно, что электроны с участков АВ и ВС должны собираться в плоскость В, с участков СР и ВЕ — в плоскость D и т. д. Соответственно, плоскости А, С, Е и т. д. должны опустошаться. Таким образом, в плоскостях В, Р и т. д., расположенных друг от друга на расстоянии пространственного периода волны E z (t ,z) , возникают сгустки Е z , электронов
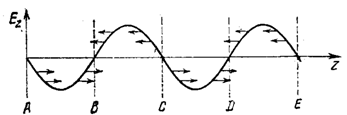
Рис. 1. К группировке электронов электрическим полем продольной составляющей замедленной бегущей волны. Распределение E z( z) показано при t=0.
При точном синхронизме, когда скорость поступательного движения электронов вдоль оси z равна фазовой скорости волны в направлении движения электронов (u = u z), электроны неподвижны по отношению к полю бегущей волны, и обмена энергией между электронами и волной нет. При u > u z сгустки обгоняют волну, чему на рис. 1. соответствует движение слева направо, т. е. против тормозящей силы. При этом кинетическая энергия движения электронов переходит в энергию СВЧ поля. Следовательно, поле усиливается. Это усиление когерентно, и при соответствующей обратной связи возникает генерация. Как обычно, генерация начинается под действием флуктуационных толчков, в поле излучения которых все более интенсивно происходит образование электронных сгустков, в свою очередь все более интенсивно испускающих электромагнитное излучение. На языке квантовой электроники это и отвечает индуцированному излучению. Лампа бегущей волны представляет собой чрезвычайно широкополосную систему. В рассмотренном случае пространственный период формирования сгустков равен L = Т u z , где Т — временной период колебаний. При спиральной замедляющей системе u z = cd/2 p а и в первом приближении не зависит от частоты поля, т. е. дисперсия отсутствует. Условия синхронизма, определяющие частоту колебаний усиливаемого поля, в этом приближении зависят только от скорости электронов, т. е. от разности потенциалов электростатического поля, ускоряющего электроны, и не привязаны к какому-либо характерному собственному пространственному периоду замедляющей структуры, которая тогда может считаться однородной. В силу своей широкополосности лампы бегущей волны обычно используются для усиления слабых сигналов СВЧ. Устройства, применяемые для создания генераторов, обычно существенно более узкополосны. Для них характерно наличие пространственно-неоднородной периодической структуры, обладающей собственными резонансами, т. е. наличие существенно дисперсионной структуры
Длина волны излучения
Рассмотрим электрон, пролетающий со скоростью V через некоторую пространственно-периодическую систему, характеризуемую пространственным периодом L . На электрон действует периодическая сила с временным периодом L / V . Следовательно, ускорение электрона меняется периодически с частотой V/ L. Этому соответствует движение по пространственно-периодической траектории. Движущийся по такой траектории электрон излучает. При существенно дорелятивистских скоростях частота излучения равна частоте периодического движения V/ L . Для макроскопических пространственных периодов L длина волны излучения нерелятивистском случае соответствует радиодиапазону.
l = с L /V
(1)
Ситуация существенно изменяется при увеличении скорости электрона. Релятивистский эффект Доплера приводит к резкому уменьшению длины волны излучения по сравнению с характерными размерами излучающей системы. При скорости электрона, близкой к скорости света (V £ с), в силу релятивистского сокращения масштаба имеем L ' = L (1 — 2 /с 2) 1/2 , при этом частота периодического воздействия на электрон в сопутствующей электрону системе координат увеличивается до значения g V/ L , где релятивистский фактор g = (1 — V 2 /с 2) -1/2 . В лабораторной системе координат обратное лоренцево преобразование приводит к релятивистскому доплеровскому увеличению частоты излучения в направлении скорости движения электрона в g (1 + V/с) раз. Для ультрарелятивистских электронов (V » c) 1 + V/с » 2 , и в результате длина волны тормозного излучения в лабораторной системе координат резко сокращается по сравнению с пространственным периодом неоднородности L:
l » L /2 g 2
(2)
Для оценки величины g удобна известная релятивистская связь между энергией W = mc 2 и массой частицы высокой энергии m = g m 0, где m , — масса покоя частицы. В физике электронных ускорителей энергию электрона обычно измеряют в электронвольтах, пользуясь соотношением W = eU , где е — заряд электрона, а U — разность потенциалов того электростатического поля, которое необходимо для ускорения электрона до скорости V . Тогда
g = eU / m 0 c 2
(3)
Как известно, энергия покоя электрона m 0 c 2 составляет 511 кэВ. Это означает, что при eU = 50 МэВ релятивистский фактор g равен g » 10 2 , так что при макроскопическом параметре L = 1 см длина волны излучения l попадает в область видимого света.
Следовательно, желая создать лазеры на свободных электронах, мы должны ориентироваться на существенно релятивистские случаи, когда
g = (1 — V 2 /с 2) - 1/2 >>1 или | V-c | << 1.
(4)
Роль релятивистских эффектов отнюдь не сводится только к резкому увеличению частоты излучения электронов. Очевидно, при релятивистской скорости электронов автоматически обеспечивается синхронизм электронного и светового пучков. Электронные ускорители, генерирующие пучки электронов сверхвысокой энергии, обычно работают в импульсном режиме.
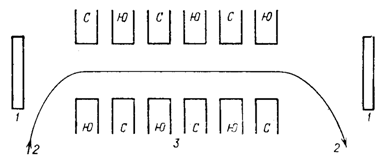
Рис. 2. Схема лазера на свободных электронах: 1 — зеркала, 2 — электронный пучок, 3 — магнитный ондулятор; С и Ю — северный и южный полюсы магнитов ондулятора.
Если за время пролета пространства взаимодействия электронов с волной электронный пакет разойдется со световой волной меньше, чем на длину волны, нарушением синхронизма можно пренебречь.
Правда существуют и слабо релятивистские приборы, подобные мазерам на циклотронном резонансе, разработанным под руководством А. В. Гапонова-Грехова, которые оказались весьма перспективными источниками коротковолнового СВЧ излучения большой мощности. С целью получения большой мощности при сравнительно низкой частоте генерации (СВЧ или дальний ИК диапазоны) обычно используются сильноточные пучки электронов не слишком высокой энергии. Продвижение в оптический диапазон требует применения электронных пучков большой энергии (см. формулу (2), которые вследствие этого обладают сравнительно низкой плотностью. В случае сильных токов существенную роль играют коллективные эффекты в плазме пучка, роль которых в создании условий для индуцированного излучения вкратце обсуждена в начале этой лекции. В случае слабых токов взаимодействие электронов с полем имеет существенно одночастичный характер. Имея в виду лазер на ультрарелятивистских электронах (g >>1), дальнейшее рассмотрение проведем в одночастичном приближении. Количественный критерий законности одночастичного подхода мы приведем в конце нашего рассмотрения.
Теория ЛСЭ; ондуляторный лазер на свободных электронах
В ондуляторном лазере на свободных электронах релятивистский электронный пучок (обычно это последовательность коротких электронных пакетов) пролетает через достаточно протяженную область, в которой магнитное поле пространственно периодично (2). Систему, обеспечивающую пространственную периодичность поля, называют ондулятором (от французского onde — волна или ondulatoire — волнообразный, волнообразователь) или виглером (от английского wiggle — покачивать, извиваться). Магнитные ондуляторы создают вблизи оси пучка постоянное во времени поперечное пространственно-периодическое линейно или циркулярно поляризованное поле.
Рассмотрим лазер со спиральным ондулятором, магнитное поле, на оси которого циркулярно поляризовано. При круговой поляризации волны, распространяющейся вдоль оси z параллельно электронному пучку, электроны находятся в полях, определяемых векторными потенциалами поля ондулятора A 1 и пола электромагнитной волны A 2,
A 1 = 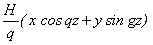
A 2 = 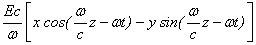
(5)
Здесь x и у — единичные векторы вдоль осей Ох и Оу, перпендикулярных друг к другу и к оси Оz; Е — напряженность электрического поля; w — частота распространяющейся вдоль Ог электромагнитной волны; q = 2 p / L (L и Н — период и напряженность магнитного поля ондулятора).
В системе координат, движущейся с первоначальной скоростью электронов V » c , потенциалы (5) принимают вид
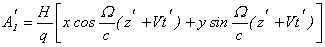
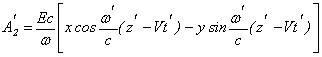
(6),
где величины со штрихом относятся к движущейся системе координат и в соответствии с (3) и (4)
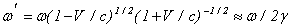 , ,
W =cq g
Первая из формул (6) показывает, что в сопутствующей системе координат потенциал поля ондулятора становится близким к потенциалу плоской волны частоты W. Другими словами, релятивистский электрон воспринимает статическое пространственно-периодическое магнитное поле как распространяющуюся навстречу ему электромагнитную волну с длиной волны L / g . Условие резонанса 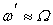 определяет ту частоту поля, в окрестности которой возможны усиление и генерация в ондуляторном лазере на свободных электронах. В лабораторной системе отсчета это условие дает значение определяет ту частоту поля, в окрестности которой возможны усиление и генерация в ондуляторном лазере на свободных электронах. В лабораторной системе отсчета это условие дает значение
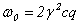
(7),
что полностью эквивалентно приведенной выше формуле (2).
Уравнения движения электрона в сопутствующей системе отсчета запишем в виде
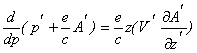
(8),
где z — единичный вектор вдоль оси Ог; р’ и V’ импульс и скорость электрона; А' = А’ 1 + А’ 2 и учтено, что А' не зависит от поперечных координат. В силу этой независимости легко написать первый интеграл уравнения (8), определяющий движение электрона в плоскости xу:
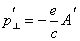
(9)
Если считать движение электрона в сопутствующей системе координат нерелятивистским, то интеграл (9) прямо определяет скорость электрона в поперечной плоскости:
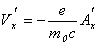 , , 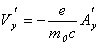
(10)
Как видно из записи (6), векторный потенциал А не имеет продольной компоненты 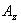 , что соответствует характеру намотки двухзаходной спирали соленоида, создающего ондуляторное поле, и поперечности распространяющейся в ондуляторе электромагнитной волны. Тогда уравнение для продольной компоненты импульса электрона , что соответствует характеру намотки двухзаходной спирали соленоида, создающего ондуляторное поле, и поперечности распространяющейся в ондуляторе электромагнитной волны. Тогда уравнение для продольной компоненты импульса электрона 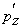 согласно (8) принимает вид согласно (8) принимает вид
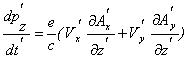
(11)
Подставив в (11) значения компонент скорости 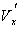 и и 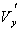 из (10), легко найти, что из (10), легко найти, что
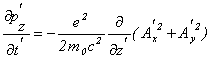
(12)
Сумма квадратов поперечных составляющих суммарного векторного потенциала А' равна
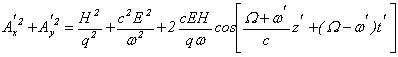
(13)
Подставляя это выражение в (11) и учитывая, что при нерелятивистском движении в сопутствующей системе координат 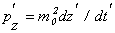 , получаем уравнение для продольной координаты электрона , получаем уравнение для продольной координаты электрона 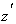 в этой системе: в этой системе:
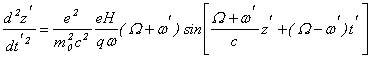
(14)
Аргумент синуса определяет фазу движения электрона в полях ондулятора и распространяющейся в нем волны:
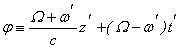
(15)
Связь фазы j с продольной координатой движения электрона г и временем t в лабораторной системе отсчета может быть получена с помощью обратного преобразования Лоренца:
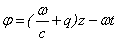
(16)
В окрестности резонанса, т. е. при 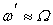 , имеем , имеем
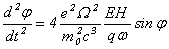
(17)
Переходя в лабораторную систему отсчета и подставляя в (17) значения 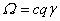 и и 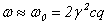 , получаем уравнение , получаем уравнение
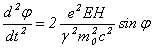
(18)
Таким образом, уравнение движения электрона в ондуляторе сводится к уравнению классического математического маятника для фазы этого движения. Это свидетельствует о наличии глубокой аналогии между лазером на свободных электронах и электронными приборами СВЧ, которые в приближении заданного поля также описываются подобными уравнениями.
Дальнейший анализ требует задания начальных условий. В момент входа электрона в ондулятор фаза имеет некоторое, вообще говоря, произвольное значение j 0. Второе начальное условие легко получить дифференцированием выражения (16), служащего определением фазы. В результате при t= 0 имеем
j = j 0
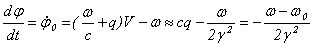
(19)
Заметим, что начальная скорость изменения фазы пропорциональна отстройке частоты излучения от резонансного значения.
Уравнение (18) с начальными условиями (19) полностью определяет движение электрона в полях волны и ондулятора и позволяет определить основные характеристики лазера.
Найдем энергию, излучаемую электроном в ондуляторе за один проход. Энергия, излучаемая в единицу времени, определяется как взятая с обратным знаком работа, совершаемая полем волны над электроном:
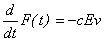
(20)
где по определению 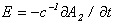 . Это уравнение позволяет установить простую связь между излучаемой энергией F и фазой j . . Это уравнение позволяет установить простую связь между излучаемой энергией F и фазой j .
Действительно, с учетом (9) поперечная скорость электрона в лабораторной системе координат равна
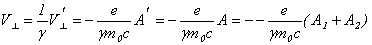
(21)
Подставляя (6) в (21), а (21) в (20), после простых преобразований получаем
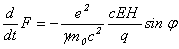
(22)
Но sin j связан с d 2 j /dt 2 уравнением маятника (18), что и дает искомую связь в достаточно простой форме:
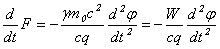
(23)
Здесь W = g m 0 c 2 — полная энергия релятивистского электрона.
Интегрирование этого уравнения с учетом начальных условий (19) для d j /dt и при естественном предположении, что F(0)=0 , дает
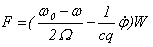
(24)
Воспользуемся далее хорошо известным первым интегралом уравнения движения маятника, который выражает закон сохранения энергии: сумма кинетической и потенциальной энергий маятника в произвольный момент времени равна их cумме в начальный момент времени t = 0 . В наших обозначениях с учетом начальных условий (19) это означает, что
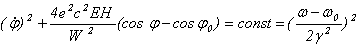
(25)
Отметим, что уровень полной энергии маятника определяется как начальной фазой j 0, так и расстройкой w - w 0 . В приближении слабого сигнала
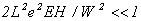
(26),
где учтено, что время прохождения электроном ондулятора длины L равно L/c , т. е. при E = 0 наш аналог маятника совершает не колебательное, а вращательное движение относительно некоторого положения равновесия, совершая полные обороты с круговой частотой (w - w 0)/2 g 2 . Это означает, что в приближении слабого сигнала уравнение (25) может решаться методом итераций по отношению к слагаемому 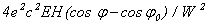 . .
Не загромождая изложение протяженными выкладками, отметим, что в нулевом порядке излучаемая энергия (24) равна нулю. В отсутствие поля электромагнитной волны нет ни излучения, ни поглощения. В следующем, первом, приближении излучаемая энергия оказывается пропорциональной cos j 0 , или sin j 0 . Но в электронных ускорителях высокой энергии электронный пучок состоит, как уже отмечалось, из электронных сгустков (электронных пакетов) конечной длительности с продольным размером, обычно не меньшим 1 мм, что существенно превышает длину волны света. Следовательно, излучаемая энергия должна быть усреднена по начальной фазе j 0.
В результате такого усреднения в первом порядке по Е излучаемая энергия обращается в нуль. Только во втором порядке итераций уравнение (25) дает отличную от нуля среднюю скорость изменения фазы, что с помощью (24) позволяет определить среднюю энергию, излучаемую электроном за один проход 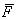 . Эта величина естественным образом связана со значением коэффициента усиления излучения за один проход по мощности 1 + G, а именно: . Эта величина естественным образом связана со значением коэффициента усиления излучения за один проход по мощности 1 + G, а именно:
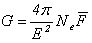
(27),
где N e — электронная плотность. В результате довольно громоздких выкладок получается выражение
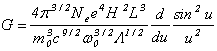
(28)
где введены обозначения 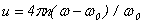 , , 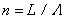 — число периодов ондулятора, L — его длина. — число периодов ондулятора, L — его длина.
Коэффициент усиления G пропорционален производной от спектральной интенсивности спонтанного излучения, что прекрасно иллюстрируется, представленными на рис. 3 результатами измерения этих величин.
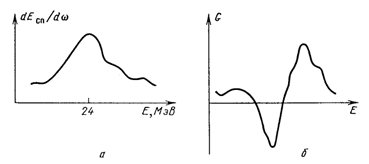
Рис. 3. Спектр спонтанного ондуляторного излучения (a) и спектральная зависимость коэффициента усиления в Лсэ (б)
Фактор 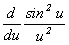 определяет дисперсионную зависимость G(w). Усиление возможно (G>0) при u<0 или w < w 0. Максимальный коэффициент усиления достигается при | u | = 1. Это условие определяет ширину полосы усиления: определяет дисперсионную зависимость G(w). Усиление возможно (G>0) при u<0 или w < w 0. Максимальный коэффициент усиления достигается при | u | = 1. Это условие определяет ширину полосы усиления:
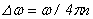
(29),
обусловленную конечной длиной ондулятора 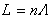 и являющуюся аналогом обычной однородной ширины линии. Подчеркнем, однако, что формула (28) получена для моноэнергетического пучка электронов. В реальных условиях дело обстоит не всегда так, и если разброс электронов по энергиям в пучке и являющуюся аналогом обычной однородной ширины линии. Подчеркнем, однако, что формула (28) получена для моноэнергетического пучка электронов. В реальных условиях дело обстоит не всегда так, и если разброс электронов по энергиям в пучке 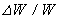 достаточно велик, то возникает неоднородное уширение, которое может оказаться более существенным, чем однородное. достаточно велик, то возникает неоднородное уширение, которое может оказаться более существенным, чем однородное.
При выполнении неравенства 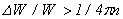 неоднородное уширение превышает однородное и формулу (28) необходимо усреднить по функции распределения электронов по энергиям f(W). В случае сильного неоднородного уширения фактор неоднородное уширение превышает однородное и формулу (28) необходимо усреднить по функции распределения электронов по энергиям f(W). В случае сильного неоднородного уширения фактор 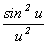 можно аппроксимировать дельта-функцией: можно аппроксимировать дельта-функцией: 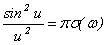 . Тогда после усреднения по W получаем . Тогда после усреднения по W получаем
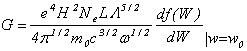
(30)
Здесь введено обозначение 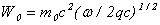 и принято, что функция распределения f (W) нормирована условием и принято, что функция распределения f (W) нормирована условием 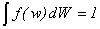 , в силу чего , в силу чего 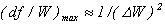 . Максимальный коэффициент усиления достигается при . Максимальный коэффициент усиления достигается при 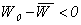 , , 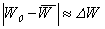 , где , где 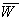 — средняя энергия электронов в пучке. Отсюда следует, что ширина полосы усиления в этом случае равна — средняя энергия электронов в пучке. Отсюда следует, что ширина полосы усиления в этом случае равна
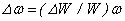
(31)
Формула (30), справедливая при 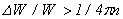 , допускает наиболее прямую аналогию с лазерами, основанными на переходах между дискретными уровнями атомов или молекул. В самом деле, условие отрицательности поглощения (G>0) выполняется, если , допускает наиболее прямую аналогию с лазерами, основанными на переходах между дискретными уровнями атомов или молекул. В самом деле, условие отрицательности поглощения (G>0) выполняется, если 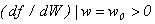 . Это означает, что усиление осуществляется электронами, соответствующими возрастающему крылу функции распределения, и наоборот, поглощению отвечает ниспадающее крыло распределения электронов по энергии. Другими словами, усиление наблюдается при условии, что число электронов с большей энергией в окрестности W 0 больше числа электронов с меньшей энергией. А это есть не что иное, как условие инверсии населенности уровней применительно к системе с непрерывным спектром. При неоднородном уширении ( . Это означает, что усиление осуществляется электронами, соответствующими возрастающему крылу функции распределения, и наоборот, поглощению отвечает ниспадающее крыло распределения электронов по энергии. Другими словами, усиление наблюдается при условии, что число электронов с большей энергией в окрестности W 0 больше числа электронов с меньшей энергией. А это есть не что иное, как условие инверсии населенности уровней применительно к системе с непрерывным спектром. При неоднородном уширении (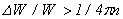 ) условием отрицательного поглощения является обычное условие инверсии населенностей в окрестности энергии W 0 определяемой частотой w и периодом ондулятора ) условием отрицательного поглощения является обычное условие инверсии населенностей в окрестности энергии W 0 определяемой частотой w и периодом ондулятора 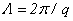 . .
Формулы (28) и (30) получены в одночастичном приближении. Вместе с тем, как уже говорилось раньше, в случае больших электронных токов существенную роль могут, вообще говоря, играть коллективные эффекты в плазме пучка. Однако если в сопутствующей релятивистским электронам системе координат произведение инкремента развития плазменных неустойчивостей на время пролета электронов через ондулятор мало, то неустойчивости не возникают и коллективными эффектами можно пренебречь. Максимальный инкремент развития неустойчивостей в плазме определяется плазменной частотой 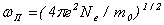 . Условием одночастичности взаимодействия является выполнение требования . Условием одночастичности взаимодействия является выполнение требования 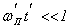 , где , где 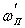 и и 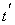 — соответственно плазменная частота и время взаимодействия в движущейся системе координат. Обратное лоренцево преобразование для времени и продольной координаты приводит к условию — соответственно плазменная частота и время взаимодействия в движущейся системе координат. Обратное лоренцево преобразование для времени и продольной координаты приводит к условию 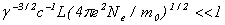 , которое для ультрарелятивистских электронов всегда выполняется с большим запасом. , которое для ультрарелятивистских электронов всегда выполняется с большим запасом.
Итак, мы видим, что пучок релятивистских электронов, распространяющихся прямолинейно в магнитном ондуляторе, способен усиливать, а значит, при соответствующей обратной связи генерировать, излучение на длинах волн, определяемых пространственным периодом ондулятора L и значением релятивистского фактора g, т. е. энергией электронов. При этом перестройка длины волны излучения естественно осуществляется изменением энергии электронов. Лазер такого типа может, в принципе, работать от волн субмиллиметрового диапазона до дальнего УФ излучения. При характерной длине ондулятора в несколько метров и пространственном периоде 1 – 3 см относительная однородная ширина линии усиления составила бы 10-4
– 10-3
. Обычно относительная немоноэнергетичность электронных пучков превышает эту величину.
Сравнительно легко в ондуляторах с помощью двойных сверхпроводящих спиралей достигается циркулярно поляризованное магнитное поле с индукцией в несколько килогаусс. В этих условиях при электронном токе в пучке в несколько ампер (Ne » 5 × 1010
– 1011
см3
) для ближней ИК-области спектра при энергии электронов 20 – 30 МэВ получено усиление за один проход в несколько процентов (порядка 10%) и генерация с выходной пиковой мощностью порядка 10 4 Вт.
Ускорители электронов, используемые как источники электронных пучков, работают обычно в импульсном режиме. Длительность импульсов электронного пучка составляет, как правило, величину порядка 1 мкс. Однако эти импульсы отнюдь не являются гладкими, а представляют собой регулярную последовательность коротких сгустков (электронных пакетов) существенно меньшей (обычно пикосекундной) длительности. В некоторых ускорителях оказывается возможным реализовать непрерывную последовательность таких сгустков.
Для замыкания цепи обратной связи необходимо, чтобы временной интервал между сгустками в регулярной последовательности их поступления на вход ондулятора был кратен двойному времени пробега излучения через резонатор. Только в этом случае излучение, созданное электронными сгустками и накопленное в резонаторе лазера при многократных отражениях от его зеркал, поступает в виде волновых пакетов на вход ондулятора синхронно с электронными пакетами и усиливается в течение всего времени существования последовательности электронных сгустков. В результате лазерная генерация осуществляется в виде последовательности коротких импульсов, разделенных интервалами времени, равными или кратными двойному времени прохода излучения между зеркалами резонатора лазера, расстояние между которыми практически равно длине ондулятора.
Немонохроматичность излучения лазера на свободных электронах определяется, таким образом, длительностью электронных сгустков. Сгустки длительностью 3 пс занимают в пространстве область протяженностью примерно 1 мм и приводят к ширине спектра излучения 10 см-1
. Увеличение монохроматичности лазеров на свободных электронах требует удлинения электронных сгустков (конечно, при условии сохранения пикового значения электронного тока).
Основные конструктивные элементы ЛСЭ
Наиболее важным физическим компонентом ЛСЭ является ускоритель. Энергия электронного пучка, создаваемого ускорителем, будет лежать в области релятивистских энергий электронов (mс 2 = 510 кэВ) и может быть выше 1000 МэВ. Ток ускорителя, как правило, является импульсным с длительностью импульса от нескольких микросекунд до нескольких пикосекунд. Ускорители могут работать в режиме либо одиночных импульсов, либо повторяющихся импульсов с частотой повторения до 1000 Гц. Электроны ускоряются диодной структурой или электронной пушкой, которые включают в себя "горячий" или "холодный" катод, фокусирующие элементы и ведущее магнитное поле. В дальнейшем, если не будет специально оговорено, будем считать, что ускорение осуществляется диодной структурой.
Другим параметром, характеризующим электронный пучок, является его собственный разброс по продольным импульсам ["холодный" пучок имеет на выходе только одно значение поперечного (или продольного) импульса при данной энергии]. В идеальном случае энергия всех электронов, вылетающих из ускорителя, должна быть одной и той же, но из-за конструктивных особенностей ускорителя и системы транспортировки у электронов имеется разброс по импульсам в поперечном и продольном направлениях. Он описывается параметром, называемым эмиттансом пучка, который характеризует яркость потока. Для ЛСЭ нужны яркие электронные потоки с малым разбросом по продольным импульсам. Это и не удивительно, если вспомнить, что в обычных лазерах излучение на выходе тоже является "ярким" (т. е. в дополнение к высокому уровню выходной мощности оптический пучок имеет очень малую расходимость и, следовательно, может быть сфокусирован до дифракционно-ограниченного пятна).
Кроме того, нам необходимо устройство, которое обеспечивало бы связь прямолинейного неизлучающего движения электронов с электромагнитной волной. Поскольку электромагнитное поле оптического пучка, распространяющегося параллельно оси движения электронов, является поперечным, для обмена энергией с электромагнитным полем электрону необходимо сообщить поперечную компоненту движения. Тогда электрон будет совершать работу над полем, записываемую математически в виде j*Е. Это осуществляется искривлением траектории электрона в периодическом поперечном магнитостатическом поле, создаваемом ондулятором. В этом случае мы имеем дело с магнитотормозным излучением. Имеется много способов, позволяющих вычислять с достаточной степенью точности траектории движения электронов в ондуляторе. Существует также много других устройств, которые могут выступать в роли ондуляторов: системы с периодическими электростатическими элементами, с электромагнитными волнами высокой интенсивности и, возможно, система с электростатической волной, которая может возбудиться при инжекции электронного пучка в специально приготовленную плазму или кристалл. Многие из этих ондуляторов менее удобны для реализации, чем магнитостатический ондулятор. Большинство же разработанных в настоящее время ондуляторов представляют собой либо спиральные токовые обмотки, либо линейную цепочку из постоянных дипольных магнитов.
Типичный период ондулятора равен примерно 3 см, а типичное значение индукции магнитного поля порядка 1 кГс. Такое поле может создаваться импульсными или постоянным током (последнее возможно в сверхпроводнике) или ондулятор можно составить из постоянных магнитов как из "строительных блоков" (таких, как самарий-кобальтовые магниты). Простейшие конструкции ондуляторов имеют обычно фиксированные значения периода и амплитуды поля, за исключением коротких участков на входе и выходе, где поле адиабатически увеличивается, чтобы обеспечивать плавный переход электронов в новую область взаимодействия. Однако можно сконструировать такой ондулятор, который при определенных условиях позволяет улучшить характеристики ЛСЭ; это привело к созданию неоднородных ондуляторов, у которых период, амплитуда или форма поля вдоль структуры изменяются адиабатически. Успешная разработка ЛСЭ с неоднородными ондуляторами значительно расширила возможности их применения и привела к новым достижениям в развитии теории лазеров на свободных электронах.
Наличие в ЛСЭ ондулятора позволяет использовать его не только для замедления электронов, но и для их ускорения. Это возможно также, например, в линейном ускорителе, в котором ускорение или замедление осуществляется продольной компонентой ВЧ электрического поля в последовательности резонаторов или в нагруженной передающей линии. Однако в линейном ускорителе взаимодействие всегда происходит на частоте ВЧ источника, в то время как в ЛСЭ оно имеет место на удвоенной частоте доплеровского сдвига. Таким образом, ондулятор — это устройство связи оптической волны и релятивистского потока электронов.
Другим важным элементом ЛСЭ являются зеркала резонаторов. Имеется некоторая тенденция считать, что вопрос о зеркалах уже решен в традиционной лазерной оптике, но это далеко не так. Совершенствование качества зеркал необходимо во всех областях лазерной физики, и это особенно важно для ЛСЭ, в частности благодаря следующим требованиям. Во-первых, это требование к коэффициенту отражения зеркал, которое является решающим для ЛСЭ с малым усилением, особенно в видимом и УФ диапазонах. Необходимо, чтобы зеркала имели устойчивое широкополосное покрытие. Получение оптимального коэффициента отражения зеркал представляет собой засекреченную область исследований, но достижение R~0,9995 в видимом диапазоне возможно благодаря использованию многослойных (например, порядка 20) интерференционных пленок, а величину R>50% можно теперь получать для длин волн порядка 100*10-10
м. Разлагая коэффициент отражения в ряд Тейлора можно получить его зависимость по радиусу. Такая зависимость может оказаться полезной при контроле неустойчивости боковых полос, которая, как полагают, может вызвать осложнения при работе ЛСЭ в режиме большого уровня мощности. Во-вторых, в случае работы ЛСЭ на накопителе, энергия электронов которого составляет 100 – 200 МэВ, мощное УФ синхротронное излучение будет очень быстро приводить к разрушению покрытия зеркал с высоким коэффициентом отражения. По этому разработка устойчивых к УФ излучению зеркальных покрытий с высоким коэффициентом отражения представляет собой необходимое условие успешной разработки ЛСЭ, использующих энергию накопительного кольца. В-третьих, в ЛСЭ с большим уровнем мощности в коротковолновом диапазоне диссипация энергии на зеркале может привести к разрушению его поверхности. Например, выходную мощность ЛСЭ, равную 10 МВт, при 1%-ном коэффициенте пропускания зеркала не следует рассматривать как очень высокую, хотя в резонаторе она будет около 1 ГВт. Небольшая доля этой мощности должна рассеиваться подложкой зеркала без прогрессирующего поверхностного разрушения. Хотя в резонаторе импульсная мощность 1 ГВт не вызывает каких-то осложнений при существующей технологии, некоторые ускорители создают электронные пучки очень высокой мощности, а это неизбежно приведет к соответствующим трудностям при реализации потенциальных возможностей ЛСЭ. Наконец, успешное развитие длинноволновых ЛСЭ связано с применением обратной связи типа распределенных отражающих элементов ("распределенная обратная связь"), разработка которых находится еще в стадии исследований.
Характер взаимодействия электронного пучка с электромагнитными модами оптического резонатора можно описать методами квантовой электроники. Между зеркалами резонатора благодаря многократному отражению оптического пучка устанавливаются поперечные и продольные моды; такой процесс впервые описали Фокс и Ли. В этом резонаторе Фабри – Перо полные потери складываются из дифракционных потерь на краях зеркал, потерь за счет диссипации излучения на поверхности зеркал и потерь, обусловленных наличием связи (через отверстие, неустойчивый резонатор или через частично пропускающее зеркальное покрытие). Электронный пучок будет осциллировать только на тех модах, взаимодействие с которыми является сильным, т. е. обеспечена связь электронного пучка с оптической структурой) и потери, для которых малы. Поскольку линия излучения ЛСЭ шире, чем у традиционного лазера, в резонаторе, если в него не внесены фильтры, могут возбуждаться многие резонаторные моды. В некоторых типах ЛСЭ в данный момент времени в резонаторе может присутствовать один электронный сгусток диаметром около 1 мм и длиной лишь несколько миллиметров. В этом случае оптическая волна будет опережать медленно распространяющийся электронный импульс и возникает эффект, названный лазерной летаргией. На выходе мы будем иметь последовательность очень коротких импульсов, возникающих за счет синхронизации мод.
Режимы работы и классификация
ЛСЭ будут работать в несколько совершенно особых режимах, в которых справедливы различные физические принципы, а для характеристики важных параметров используется весьма широкая терминология. Здесь мы кратко рассмотрим режимы работы и соответствующую классификацию.
Если ток электронного пучка мал и энергия пучка высока (например, 20 МэВ), а длина волны излучения лежит в коротковолновом (ИК) диапазоне, то мы имеем режим ЛСЭ, который называют по-разному: комптоновский, двухволновый, интерференционный или режим одночастичного взаимодействия. В этом случае существует очень близкая аналогия между ЛСЭ и линейным ускорителем: увеличение (уменьшение) энергии частиц соответствует затуханию (усилению) энергии электромагнитного поля. Оптимальное усиление ЛСЭ зависит от того, насколько правильно мы выберем энергию пучка и длину ондулятора; по этому такой режим называют еще и режимом конечной длины ондулятора. К ЛСЭ в общем случае неприменимо положение лазерной физики, согласно которому чем больше объем среды, тем больше усиление и выходная мощность. Кроме того, ни о каком усилении не может быть и речи, когда в ЛСЭ оптический пучок отражается от зеркала и движется навстречу потоку электронов.
Лазеры на свободных электронах, в которых имеет место экспоненциальное нарастание волн и которые напоминают традиционные лазеры с накачкой, работают в длинноволновом режиме (l >100 мкм) при низкой энергии (обычно менее 5 МэВ) и при высоких плотностях тока пучка (j>1000 А/см 2); эти ЛСЭ представляют собой компактные устройства с высоким коэффициентом усиления. Если пучок холодный (т. е. разброс электронов по импульсам невелик), а амплитуда поля накачки ондулятора мала, то мы имеем ЛСЭ на комбинационном рассеянии. При увеличении поля накачки ондулятора коэффициент усиления возрастает, и мы приходим к режиму большой амплитуды накачки с оптимальными значениями усиления и эффективности (его еще иногда называют режимом осциллирующей двухпотоковой неустойчивости). Однако если пучок имеет большой разброс по импульсам, усиление и мощность уменьшаются, но сигнал все еще экспоненциально нарастает вдоль ондулятора, то такой режим называют комптоновским с разбросом по импульсам. Усиление уменьшается потому, что ЛСЭ на комбинационном рассеянии — это трехволновое параметрическое устройство (волна накачки, сигнал и холостая волна), в котором в качестве холостой волны может выступать либо плазма, либо волна пространственного заряда. В случае электронов с разбросом по импульсам, когда холостая волна затухает вследствие бесстолкновительного эффекта (за счет затухания Ландау), мы снова возвращаемся к режиму малого усиления. (Все ЛСЭ требуют, чтобы электронный пучок был достаточно холодным.).
Между одночастичными ЛСЭ и ЛСЭ, в которых существенную роль играют коллективные эффекты, приводящие к экспоненциальному нарастанию усиления, можно провести довольно простую границу. ЛСЭ действуют в коллективном (многочастичном) режиме, когда система имеет достаточно большую длину, а пучок — достаточно высокую плотность, так что вдоль системы укладывается несколько плазменных длин волн. Это накладывает верхний предел на энергию пучка и нижний предел на длину волны. Другим весьма важным эффектом является взаимодействие между силой, которая группирует электроны пучка (будем называть ее пондеромоторной силой), и расталкивающими силами пространственного заряда. Пондеромоторная сила определяется амплитудами ондуляторного поля и сигнала, в то время как силы пространственного заряда — плотностью тока и энергией пучка. Из-за этой конкуренции сил усиление ЛСЭ в некоторых случаях возрастает, а в некоторых уменьшается.
Как и традиционные лазеры на атомных переходах, ЛСЭ могут работать и как усилители когерентного излучения, и как генераторы (при использовании резонатора с зеркалами), или как усилители локального шума. Последний случай в соответствии с оптической терминологией мы называем ЛСЭ на сверхизлучении. Такой ЛСЭ при очень большом усилении может давать мощное частично когерентное излучение.
Экспериментальные исследования ЛСЭ на однородных ондуляторах
Самые первые эксперименты по ЛСЭ были проведены в Станфорде на SCA. В табл. 1 представлены типичные экспериментальные параметры.
Таблица 1. Параметры ЛСЭ-генератора Станфордского университета
| Электронный пучок |
| Энергия пучка |
43 МэВ |
| g |
69 |
| Пиковый ток |
1,3 А |
| Протяженность импульса |
1 мм |
| Расстояние между импульсами |
25,4 мм |
| Радиус пучка |
0,25 мм |
| Ондулятор |
| Период |
3,3 см |
| Амплитуда спирального поля |
2,3 кГс |
| Длина |
5,3 м |
| Резонатор |
| Расстояние между зеркалами |
12,7 м |
| Потери в резонаторе за проход туда и обратно |
2,8 % |
| Потери на связь в резонаторе |
1,5 % |
| Длина волны |
3,3 мкм |
| Размер пятна |
0,167 см |
| Рэлеевская длина волны |
2,7 м |
| Коэффициент заполнения |
0,017 |
| Коэффициент потерь на спонтанное излучение |
0,05 |
| Радиус зеркал |
7,5 м |
Ондулятор изготовлен из сверхпроводящей бифилярной спиральной обмотки; для отклонения электронного пучка от зеркал (рис. 4) использовалось продольное магнитное поле 1 кГс. В статье Элиаса и др. сообщалось о том, что зарегистрировано спонтанное излучение из ондулятора на длине волны 10,6 мкм при энергии W » 24 МэВ и усиление около 7 % сигнала от TEA С0 2 -лазера с плотностью мощности 140 кВт/см2
, причем была получена всем теперь знакомая асимметричная кривая усиления. Этот эксперимент был повторен на накопителе АСО (Орсе, Франция) при энергии 150 МэВ. На рис. 5 показано очень точное соответствие между коэффициентом усиления ЛСЭ и производной спектра спонтанного излучения (аргоновый лазер, 4880 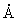 ). После увеличения импульсного тока SCA от 70 мА до 2,6 А стало возможным продемонстрировать генерацию лазера на длине волны 3,4 мкм, когда энергия электронов была 43,5 МэВ. Превышение импульсной мощности над уровнем мощности спонтанного излучения было порядка 108
. При коэффициенте пропускания зеркал 1,5% в резонаторе зарегистрирована мощность ~500 кВт ). После увеличения импульсного тока SCA от 70 мА до 2,6 А стало возможным продемонстрировать генерацию лазера на длине волны 3,4 мкм, когда энергия электронов была 43,5 МэВ. Превышение импульсной мощности над уровнем мощности спонтанного излучения было порядка 108
. При коэффициенте пропускания зеркал 1,5% в резонаторе зарегистрирована мощность ~500 кВт
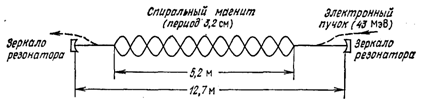
Рис. 4. Схема Станфордского лазера на свободных электронах в режиме генератора. Около зеркал, кроме поля ондулятора, использовалось ведущее поле для ввода и вывода электронного пучка. © 1977 APS
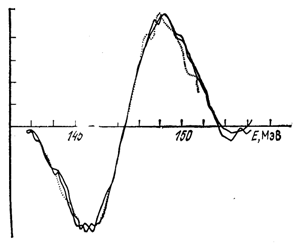
Рис. 5. Сравнение кривых усиления ЛСЭ (аргоновый лазер, 4880 А), измеренного в двух отдельных экспериментах (сплошные линии), наложенных на производную спектра спонтанного излучения (пунктирная кривая). Максимальное усиление равно 3 · 10-4
; использовался сверхпроводящий ондулятор с периодом l 0 = 4 см. © 1982 North-Holland.
На рис. 6 для сравнения приведен спектр мощности ниже (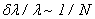 ) и выше порога генерации, из которого видно, что оптический резонатор значительно сужает ширину линии. Все эксперименты были выполнены для двухволнового режима ЛСЭ, поскольку w p T~0,1. ) и выше порога генерации, из которого видно, что оптический резонатор значительно сужает ширину линии. Все эксперименты были выполнены для двухволнового режима ЛСЭ, поскольку w p T~0,1.
Особенно большую ценность имеют дополнительные экспериментальные результаты, полученные Станфордской группой, поскольку они обеспечивают базу для разработки надежной теории. Один из результатов (рис. 7) связан с временем “включения” генератора. Это время оказалось не только удивительно большим (~30 мкс, несколько сотен проходов оптического пучка), но и было обнаружено, что время включения и мощность выходного излучения очень чувствительны к расстоянию между зеркалами резонатора (рис. 8). Изучение времени нарастания мощности излучения в начале импульса генератора позволило оценить коэффициент усиления малого сигнала за проход, который оказался равным 6 – 10%.
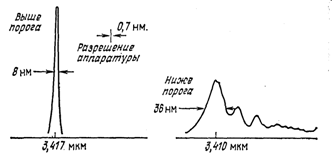
Рис. 6. Сужение спектральной линии излучения ЛСЭ выше и ниже порога генерации. © 1977 APS
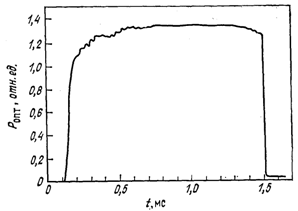
Рис. 7. Форма импульса излучения ЛСЭ, показывающая задержку времени включения генератора и времени нарастания; время на оси абсцисс отсчитывается от момента выстрела электронного пучка. © 1982 Addison-Wesley
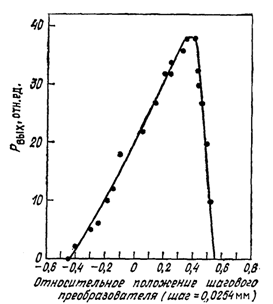
Рис. 8. Зависимость средней выходной мощности ЛСЭ от расстройки длины резонатора. © 1982 Addison-Wesley
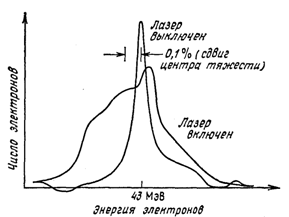
Рис. 9. Влияние излучения ЛСЭ на энергетический спектр электронов. © 1977 Addison-Wesley
Были проведены измерения временных характеристик электронного и оптического спектров. Ширина распределения электронов по импульсам возрастает примерно на 1% при включении лазера (в качестве примера на рис. 9 приведен один из предыдущих результатов, из которого видно, что центр тяжести кривой смещен примерно на 0,1% относительно начальной энергии электрона). Мы видим, что спектр является асимметричным. После первоначального запуска лазера среднее значение оптической длины волны, по существу, сохраняется постоянным, но все еще некоторые особенности оптического импульса нуждаются в экспериментальной проверке. Недавно были проведены эксперименты, в которых ширина оптического импульса измерялась с помощью автокорреляционной схемы и генерации второй гармоники в кристалле LiNbO3
. Когда длина резонатора была точно синхронизирована с протяженностью сгустка, наблюдался импульс ЛСЭ длительностью 1,5 пс при импульсной мощности около 400 кВт. При изменении длины резонатора было зарегистрировано увеличение ширины оптического импульса и уменьшение ширины спектральной линии излучения.
В связи с исследованиями, проводимыми в Станфорде на SCA, необходимо упомянуть об успешных экспериментах Лаборатории передовой технологии и инженерных наук фирмы “TRW” с ЛСЭ-генератором, в котором используется многокомпонентный ондулятор. Этот эксперимент отличает наличие очень хорошей диагностической и контрольно-измерительной аппаратуры. На однородном и неоднородном вариантах ондулятора была получена средняя мощность излучения 10 Вт на длине волны 1,6 мкм. Кроме того, во время генерации было обнаружено интенсивное излучение третьей гармоники на длине волны около 0,5 мкм. Как и можно было предполагать, это коротковолновое излучение оказалось чрезвычайно чувствительным к регулировке длины резонатора.
Применения ЛСЭ
Краткий анализ спектра (рис. 10) показывает, что ЛСЭ должны быть наиболее перспективными для той спектральной области, для которой разработано очень немного источников когерентного излучения, например для субмиллиметрового и УФ диапазонов.
Пока еще рано сравнивать ЛСЭ с более высокоразвитыми ЛЭС лазерными системами, поскольку для них еще мало что сделано, в области специальных источников питания и ускорительных установок. Однако ясно, что в субмиллиметровой области спектры, ЛСЭ займут не больше места, чем обычные субмиллиметровые молекулярные лазеры. Даже в ближнем ИК диапазоне и видимой области спектра ЛСЭ могут конкурировать с традиционными лазерами только в тех случаях, когда важную роль играют перестройка частоты, выходная мощность или КПД.
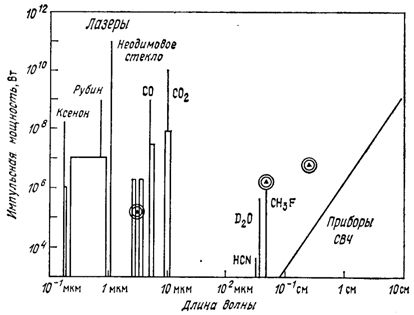
Рис. 10. Когерентные источники большой мощности; двойными кружками указаны ЛСЭ
В области спектра, представляющей интерес для химиков (200 – 4000 см-1
), наличие перестраиваемого по частоте источника позволило бы качественно повысить эффективность применения колебательной спектроскопии поглощения молекул. Длительность импульса ЛСЭ может быть меньше времени релаксации молекул; следовательно, можно с высокой точностью контролировать химические процессы с участием выделенных связей. Применение высокоэффективного ЛСЭ позволит нам не только лучше понять химические цепные реакции с лазерным возбуждением, когда фотодиссоциация одной молекулы будет приводить к образованию большого числа других, но и приблизит их к реализации в промышленных масштабах. В дальнем ИК-диапазоне (~100 мкм), где энергия фотонов равна примерно kt , ЛСЭ можно было бы использовать для исследования низкоэнергетических состояний Ван-дер-Ваальса. Возможность широкой перестройки частоты и высокая эффективность делают ЛСЭ весьма привлекательными для лазерного разделения и обогащения изотопов.
Другим весьма полезным свойством некоторых ЛСЭ является возможность работы в режиме коротких импульсов (в случае применения для этих целей микротрона, линейного ускорителя или накопительного кольца). Короткие импульсы (рис. 11) длительностью несколько пикосекунд весьма эффективны для исследования различных видов возбуждений (рис. 12).
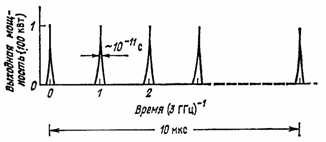
Рис. 11. Схематическое изображение мощного импульса ЛСЭ на линейном ускорителе. Пики — микроимпульсы, которые в совокупности образуют макроимпульс длительностью несколько микросекунд с частотой повторения несколько герц

Рис. 12. Применения ЛСЭ в физике твердого тела. (Согласно Шоу и Пателу)
До появления ЛСЭ источники излучения в дальнем ИК диапазоне и в субмиллиметровой области спектра имели низкий уровень мощности и не перекрывали весь диапазон, а приемники были весьма дорогими или имели невысокую чувствительность. Однако с помощью ЛСЭ в дальнем ИК диапазоне можно получить множество важных результатов в области физики твердого тела (рис. 13).

Рис. 13. Применение ЛСЭ в физике твердого тела. (Согласно Шоу и Пателу)
Такие работы были поставлены в фирме “Белл лэборэтриз”. Главные возможности импульсного ЛСЭ дальнего ИК-диапазона должны проявиться в нелинейной спектроскопии и при изучении переходных процессов. Нелинейная спектроскопия включает в себя изучение явлений вынужденного испускания, неупругого рассеяния от возбужденных электронов, влияния оптической накачки и т. д. К переходным процессам относятся механизмы преобразования энергии в молекулах, твердых телах и жидкостях, а также релаксация горячего электронно-дырочного газа в полупроводниках. Короткие импульсы дальнего ИК излучения можно использовать при исследованиях локальной электрической проводимости, в то время как импульсы ЛСЭ в видимом диапазоне — для рождения свободных носителей. Кроме того, с помощью ЛСЭ можно будет исследовать времена рассеяния квазичастиц в сверхпроводниках, изучать процессы распространения и взаимодействия фононов, а также характер возбуждения и релаксации двумерного электронного газа в МОП-транзисторах.
Несомненно, одна из наиболее актуальных и важных проблем в физике полупроводников, которая может быть изучена с помощью субмиллиметровых ЛСЭ, — это проблема горячих электронов. Развитие миниатюризации полупроводниковых элементов приводит к появлению нетепловых распределений электронов, поскольку в сильных электрических полях ширина запрещенной зоны оказывается порядка 1В. Вопрос о влиянии горячих электронов изучен недостаточно полно; поэтому ЛСЭ как источник субмиллиметрового излучения должен оказаться полезным как для создания этих носителей, так и для исследования их поведения в переходном режиме.
Разработка ЛСЭ на длине волны l ~0,5 мм с высоким уровнем средней мощности позволит применить его для нагрева плазмы, удерживаемой сильным магнитным полем, с помощью электронно-циклотронного резонанса или в исследованиях по термоядерному синтезу для нагрева и диагностики высокотемпературной плазмы (большое значение b = 8 p nT/B 2). В лазерном термоядерном синтезе для обеспечения энергии на мишени около 1МДж необходимо иметь источник излучения высокой мощности с длиной волны около 1/3 мкм, работающий в режиме коротких импульсов с общим КПД, равным нескольким процентам. Таким образом; можно надеяться, что в будущем ЛСЭ внесут свой вклад и в эту программу исследований.
Дистанционное зондирование верхних слоев атмосферы (на высотах 100 – 500 км) методами резонансной флуоресценции и создание лазера для спектроскопии молекул представляют собой другую область применения ЛСЭ с целью диагностики. ЛСЭ позволит разработать радарные системы высокого разрешения.
До сих пор не существует ЛСЭ, генерирующих излучение в УФ области; перестраиваемые интенсивные источники УФ излучения могут найти многочисленные применения, в частности в физике твердого тела, но до тех пор, пока не удастся преодолеть технических трудностей, нам придется довольствоваться спонтанным излучением электронов, получаемым из ондуляторов в высокоэнергетических накопителях, которые пригодны и для получения синхротронного излучения. Можно надеяться, что проводимое в настоящее время совершенствование технологии изготовления зеркал и разработка специальных ускорителей позволят получить действующий ЛСЭ в УФ диапазоне до 1990 г. Разработка ЛСЭ рентгеновского диапазона имела бы неоценимое значение для таких целей, как изготовление оптических устройств высокого разрешения методами рентгеновской интерферометрии и голографии.
Найдут ЛСЭ применение и в лазерной хирургии и в фоторадиационной медицине. Небольшой размер пятна и возможность перестройки частоты означают, что в хирургии можно получить оптимальный эффект для конкретной облучаемой ткани в зависимости от длины волны при воздействии излучения ЛСЭ. В фоторадиационной медицине введенные предварительно в ткани красители активируются на определенных длинах волн. При активации красители выделяют свободный кислород и убивают клетку без хирургического вмешательства. Красители могут присоединяться к антителам, которые под действием лазерного света высвобождаются в определенных местах. Использование перестраиваемых лазеров позволит применять для этих целей различные типы красителей. Маломощные ЛСЭ можно устанавливать непосредственно в больницах.
Ускорители, используемые в физике высоких энергий, чрезвычайно громоздки, и в настоящее время ведутся исследования, направленные на получение более высоких ускоряющих полей, которые позволят сократить размеры ускорителей и увеличить энергию частиц. Известно, что сфокусированные высокоинтенсивные лазерные поля могут создавать поперечные электрические поля напряженностью порядка 109
В/см; это можно было бы использовать в ускорителе на ЛСЭ, чтобы ускорить поток позитронов или электронов, пролетающих в ондуляторе. Увеличение энергии частиц может быть достигнуто за счет последовательного изменения периода ондуляторного поля. Изменение начального периода ондулятора от 10 см до нескольких метров позволит на длине в несколько километров получить энергию электронов более 100 ГэВ. Трудность здесь состоит в том, чтобы поддержать интенсивный лазерный пучок сфокусированным на таком большом расстоянии; Пеллегрини предложил для решения данной проблемы использовать оптические волноводы. Если реализация этого предложения будет успешной, то ЛСЭ вернет свой долг физике ускорителей.
Библиографический список
- Карлов Н. В “Лекции по квантовой электронике” учеб. пособие — М.: Наука, 1983
- “Генераторы когерентного излучения на свободных электронах”: сб. статей, пер. с англ. под ред. А. А. Рухадзе — М.: Мир, 1983
- Федоров М. В. “Электрон в сильном световом поле” — М: Наука, 1991
- Маршалл Т. “Лазеры на свободных электронах” пер. с англ. — М: Мир, 1987
|