Задача
2.
Постройте ряд распределения студентов по успеваемости: 2, 3, 3, 4, 2,
5,
5, 3, 3, 4, 5, 4, 5, 5,
5, 4, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 4, 4, 4.
Подсчитайте локальные и накопительные частоты. Постройте полигон и кумуляту распределения. Определите моду, медиану, среднюю, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
Решение:
Ряд распределения – это ряд чисел, в котором значение изучаемого признака (варианты), расположены в определенном порядке: либо в порядке возрастания, либо убывания. Наряду с вариантами ряд распределения включает и частоты – величины, показывающие сколько раз каждая варианта встречается в данной совокупности. Сумма частот равна объему совокупности. Таким образом, ряд распределения состоит из вариант (х) и частот (f
)
В зависимости от прерывности или непрерывности варьирующего признака ряды распределения удобно представлять в виде двух разновидностей: дискретного и вариационного (интервального). Дискретный ряд представляет собой ряд прерывных чисел. Например, распределение студентов по успеваемости (табл. 1). При непрерывной вариации распределение признака называется интервальным. Частоты относятся ко всему интервалу.
В зависимости от вида ряда распределения по-разному можно изобразить их графически. Если ряд дискретный – строится полигон
распределения. Величина признака откладывается на оси абсцисс, частоты – на оси ординат. Вершины ординат соединяются прямыми линиями. Гистограмма
распределения отличается от полигона тем, что на оси абсцисс берутся не точки, а отрезки, изображающие интервал, т.е. гистограмма, строится на
| Оценка (балл) |
Число студентов (частоты) |
Накопленные |
| 2 |
2 |
2 |
| 3 |
8 |
10 |
| 4 |
12 |
22 |
| 5
|
8 |
30 |
| Итого |
30 |
В основе вариационного (интервального) ряда. По накопленным частотам строится кумулятивная кривая (кумулята).
Для определения средней арифметической надо сложить все варианты и полученную сумму разделить на число единиц, входящих в совокупность (объем совокупности). Средняя арифметическая бывает простая и взвешенная. Простая средняя используется тогда, когда каждая варианта встречается лишь один раз (1). Если каждая варианта встречается несколько раз, то следует подсчитать частоты и умножить (взвесить) каждую варианту на соответствующую частоту (2).
Простая средняя арифметическая х = (1)
Средняя арифметическая взвешенная х = (2)
Средний процент влажности найдём по формуле средней арифметической взвешенной:
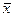 = =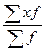 = =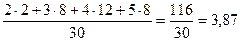
При расчете средней арифметической для интервального ряда нужно сначала определить середины интервалов как полусуммы значений верхней и нижней границ интервала. При наличии интервалов, где <хоткрыты» верхняя или нижняя граница, величину интервала определяют по последующему или предыдущему интервалу.
Реклама

Для характеристики рядов распределения кроме средней степенной применяются структурные средние: мода и медиана.
Мода
– варианта, которая наиболее часто встречается в данной совокупности, т.е. варианта с наибольшей частотой. Мо=4
Медиана
– варианта, находящаяся в середине ряда распределения.
Мода для дискретного ряда определяется просто и соответствует варианте с наибольшей частотой.
Медиану для дискретного определяют по накопленным частотам делением объема совокупности пополам: по таблице 1 – 30:2=15. Это соответствует медиане, равной 4.
Размах вариации
– разность между наибольшей и наименьшей вариантой:
R
=
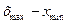 =5–2=3 =5–2=3
Среднее квадратическое отклонение
– показатель вариации, измеряющий величину, на которую все варианты в среднем отклоняются от средней арифметической.
Квадрат среднего квадратического отклонения называется дисперсией,
или средним квадратом отклонений.
Найдем дисперсию:
s2
=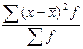 = =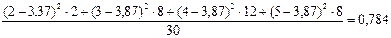
s=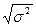 =0,885 – среднее квадратическое отклонение. =0,885 – среднее квадратическое отклонение.
Наряду с абсолютным показателем колеблемости признака – средним квадратическим отклонением – широко применяется и относительный показатель – коэффициент вариации, который показывает меру колеблемости признака относительно его среднего значения и измеряется в процентах.
V=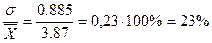
Задача 12.
Используя данные задачи 2, проверьте при уровне значимости 0,05 гипотезу о нормальном законе распределения студентов по успеваемости.
Решение:
Применяем критерий согласия – Пирсона.
Каждому ряду распределения достаточно большой совокупности объективно свойственна определенная закономерность. Моделирование кривой распределения позволяет в компактной форме дать характеристику закономерности распределения, используя ее в планировании и прогнозировании. Одним из наиболее распространенных законов распределения, применяемых в качестве стандарта, с которым сравнивают другие распределения и которое имеет важное значение для решения задач выборочного наблюдения является нормальное распределение. для того чтобы установить, верно, ли предположение о том, что эмпирическое распределение подчиняется закону нормального распределения, необходимо сравнить его с теоретическим распределением. Важно определить, являются ли различия между ними результатом действия случайных причин или обусловлены неправильно подобранной функцией.
Реклама

Критерий X-Пирсона:
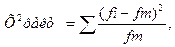
Значение Х 2факрi,
рассчитывается по изложенной выше формуле, для которой предварительно определяются теоретические частоты.
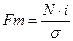
Нормированное отклонение определяется по формуле:
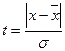
Таблица – Эмпирическое и теоретическое распределение студентов по успеваемости
| Оценка балл |
Число студентов |
t |
F(t) |
fm |
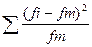 |
| 2 |
2 |
2,1 |
0,0880 |
3 |
0,3 |
| 3 |
8
|
0,98 |
0,2017 |
7 |
0,14 |
| 4 |
12 |
0,15 |
0,3212
|
11 |
0,09 |
| 5 |
8 |
1,28 |
0,2617 |
9 |
0,11 |
| Итого |
30 |
х |
Х |
30 |
0,64 |
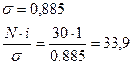
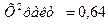
Х 2 табл
8,95
при уровне значимости 0,05 и числе степеней свободы число интервалов – 1.
Так как Х 2 факт
<
Х 2 табл
критического (допустимого) значения, то эмпирическое распределение соответствует нормальному.
Задача
27.
На основании данных таблицы б (с 1 по 26 предприятие) о выпуске продукции и размере прибыли постройте аналитическую группировку, а также исследуйте наличие и характер взаимосвязи между ними. Рассчитайте коэффициент корреляции, детерминации. Сделайте выводы.
Таблица 6– Исходные данные деятельности предприятий, млн. руб.
№
предприятия
|
– Выпуск продукции, |
Среднегодовая стоимость ОПФ, |
Численность работающих, чел. |
Потери рабочего времени, тыс. чел. дн. |
Прибыль. |
| 1 |
65,0
|
54,6
|
340 |
66,0 |
15,7 |
| 2 |
78,0 |
73,6 |
700 |
44,0 |
18,0 |
| 3 |
41,0 |
42,0 |
100 |
91,0 |
12,1 |
| 4 |
54,0 |
46,0 |
280 |
78,0 |
13,8 |
| 5
|
66,0 |
62,0 |
410 |
57,4 |
15,5 |
| 6 |
80,0 |
68,4 |
650
|
42,0 |
17.9 |
| 7 |
45,0 |
36,0 |
170 |
100,0 |
12,8 |
| 8 |
57,0 |
49,6 |
260 |
79,8 |
14,2 |
| 9 |
67,0 |
62,4 |
380 |
57,0 |
15,9 |
| 10 |
81,0 |
71,2 |
680 |
38,0 |
17,6 |
| 11 |
92,0 |
78,8 |
800 |
23,1 |
18,2 |
| 12 |
48,0 |
51,0 |
210 |
112,0 |
13,0 |
| 13 |
59,0 |
60,8 |
230 |
72,0 |
16,5 |
| 14 |
680 |
69,0 |
400 |
55,7 |
16,2 |
| 15 |
83,0 |
70,4 |
710 |
36,0 |
16,7 |
| 16 |
52,0 |
50,0 |
340 |
85,2 |
14,6 |
| 17 |
62,0 |
55,0 |
290 |
72,8 |
14,8 |
| 18 |
69,0 |
58,4
|
520 |
54,6
|
16,1 |
| 19 |
850 |
83,2 |
720 |
37,0 |
16,7 |
| 20 |
70,0 |
75,2
|
420 |
56,4
|
15,8 |
| 21 |
71,0 |
67,2 |
420 |
56,0
|
16,4
|
| 22 |
64,0 |
64,2 |
400 |
70,4 |
15,0
|
| 23 |
72,0 |
65,0
|
430 |
53,6
|
16,5 |
| 24 |
88,0 |
76,2 |
790 |
34,9 |
18,5 |
| 25
|
73,0 |
68,0 |
560
|
55,4
|
16,4 |
| 26 |
740 |
65,6
|
550
|
52,0 |
16,0 |
27
28
|
96,0 |
87,2 |
810 |
20,4 |
19,1 |
| 75,0
|
71,8 |
570
|
53,1 |
16,3 |
| 29 |
101,0 |
96,0 |
820 |
12,0 |
19,6 |
| 30 |
76,0 |
69,2 |
600 |
46,0 |
17,2 |
Решение:
Результаты группировки сведем в групповую таблицу, которая имеет вид:
Таблица 4 – Пример групповой таблицы
| Группы предприятий по…(факторный признак ВП) |
Число предприятий Вгруппе |
Факторный признак (ОПФ) |
Результативный признак (Прибыль) |
| всего |
в среднем
на 1 пред –
приятие |
всего |
в среднем
на 1 пред –
приятие |
всего |
в среднем
на 1 пред –
приятие |
41–58
58–75
75–92
|
6
13
7
|
274,6
827,4
521,8
|
45,77
63,65
74,5
|
80,5
206,8
123,6
|
13,4
15,9
17,66
|
| Итого в среднем |
26 |
1623,8 |
62,45 |
410,9 |
15,8 |
Найдем коэффициент детерминации и корреляции по формулам:

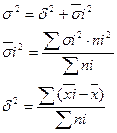
 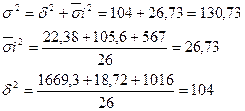
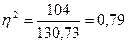 -эмпирический коэффициент детерминации -эмпирический коэффициент детерминации
Найдем коэффициент корреляции рангов Спирмена по формуле
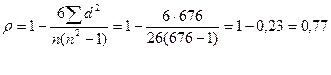
Полученное значение коэффициента спирмена свидетельствует об очень тесной связи между стоимостью основных производственных фондов и прибылью.
Задача 40
Известны темпы прироста выпуска продукции предприятия в 1999–2005 гг., процент по отношению к предыдущему году:
Таблица 12 – Темпы прироста выпуска продукции предприятия
| 1999 г. |
2000 г. |
2001 г. |
2002 г. |
2003 г. |
2004 г. |
2005 г. |
| 2 |
1 |
-3 |
-5 |
2 |
4 |
5 |
Определите:
1) базисные темпы роста (1998 г. – 100%) выпуска продукции предприятия;
2) среднегодовой темп роста и прироста.
Решение:
| Год |
1999 г. |
2000 г. |
2001 г. |
2002 г. |
2003 г. |
2004 г. |
2005 г. |
| Темп прироста |
2 |
1 |
-3 |
-5 |
2 |
4 |
5 |
| Темп роста |
102 |
101 |
97 |
95 |
102 |
104 |
105 |
Расчет будем производить по формулам:
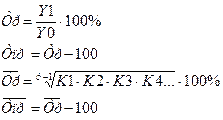
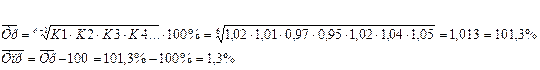
Задача 46.
Имеются данные о продаже картофеля на рынках города в мае месяце:
Таблица 17-Продажа картофеля на рынках города
| № рынка |
Средняя цена, руб. |
Продано, тыс. кг. |
| 1 |
8,0 |
70 |
| 2
|
7,8 |
25 |
| З |
8,2 |
30 |
Определите среднюю цену реализации картофеля по 3 рынкам города, среднее квадратическое отклонение и коэффициент вариации цены. Сделать выводы.
Решение:
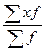
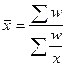 = =
s2
= = =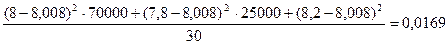
s=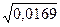 =0,13 – среднее квадратическое отклонение. =0,13 – среднее квадратическое отклонение.
V=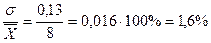
Задача 60
Имеются следующие данные о продаже товаров:
Таблица 30 – данные о продаже товаров
| Товары |
Базисный период |
Отчетный период |
цена за
единицу, руб. |
количество,
тыс, руб. |
цена за
единицу, руб. |
количество,
тыс, руб. |
| А |
30 |
10 |
40 |
9 |
| Б |
8 |
20 |
12 |
30 |
| В |
12 |
5
|
20 |
6 |
Определите:
1) общие индексы цен. физического объема, товарооборота;
2) абсолютное изменение товарооборота и влияние на него отдельных факторов.
Решение:
Будем использовать следующие формулы:
Абсолютный и относительный прирост стоимости реализованной продукции в текущем году по сравнению с базисным:
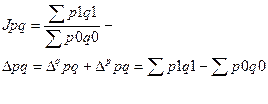
Изменение общей стоимости за счет отдельных факторов:
1) За счет изменения количества(q)
В индексной системе:
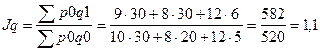
В абсолютном выражении
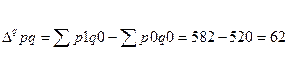
2) за счет изменения цен на продукцию(p)
В индексной системе:
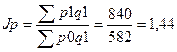
В абсолютном выражении:
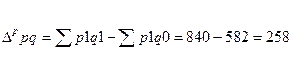
Общее абсолютное изменение результативного показателя составит алгебраическую сумму абсолютных изменений за счет отдельных факторов:
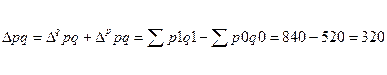
|