Учреждение образования ‹‹БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ››
Факультет ‹‹ХТиТ ››
Кафедра ‹‹ТМ ››
Специальность «1-36 07 01»
Специализация ‹‹МиОПСМ»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
КУРСОВОГО ПРОЕКТА
по дисциплине ‹‹ Теория механизмов и машин ››
Тема : ”Вертикальный пресс”
Исполнитель
студент 3 курса группы 3А Вареник Ю.А.
Руководитель Ласовский Р.Н.
Курсовой проект защищен с оценкой
Руководитель Ласовский Р.Н.
Минск 2007
Содержание
Введение
Реферат
1 Динамический синтез рычажного механизма
1.1 Задачи и методы динамического синтеза и механизма
1.2 Структурный анализ механизма
1.3 Кинематический синтез рычажного механизма
1.4 Описание построения планов аналогов скоростей
1.5 Определение приведенных моментов инерции
1.6 Определим силы сопротивления
1.7 Расчет приведенных моментов сил
1.8 Описание построения диаграмм работ, изменения кинетиской энергии, диаграммы Виттенбауэра
1.9 Определение момента инерции маховика
1.10 Определение закона движения звена приведения
2 Динамический анализ рычажного механизма
2.1 Задачи динамического анализа рычажного механизма
2.2 Кинематический анализ
2.3 Определение инерционной нагрузки
2.4 Силовой расчет
3 Синтез зубчатого зацепления
3.1 Проектирование цилиндрической эвольвенты зубчатой передачи внешнего зацепления
3.2 Геометрический синтез планетарного механизма
4 Синтез кулачкового механизма
4.1 Задачи синтеза кулачкового механизма
4.2 Определение кинематических характеристик
4.3 Определение основных размеров
4.4 Построение профиля кулачка
4.5 Расчет коэффициента жесткости пружины
Заключение
Список использованных источников
Введение
-проектирование структурной и кинематической схемы рычажного механизма по заданным основным и дополнительным условиям
-анализу режима движения механизма при действии заданных сил
-учет сил трения в кинематических парах и определение коэффициента полезного действия
-проектирование зубчатых рядовых и планетарных механизмов
-расчет оптимальной геометрии зубчатых зацеплений выходного звена
-определение мощности и выбор типа движения.
Задание на курсовое проектирование содержит название темы проекта, краткое описание назначения машины или прибора и функции их исполнительных органов и элементов, схемы согласованности перемещений исполнительных органов, исходные данные.
Реферат
ГЛАВНЫЙ ВЕКТОР СИЛ ИНЕРЦИИ, ДИНАМИЧЕСКАЯ МОДЕЛЬ, ЗУБЧАТОЕ ЗАЦЕПЛЕНИЕ, КУЛАЧКОВЫЙ МЕХАНИЗМ, МАХОВИК, ОСЬ ВРАЩЕНИЯ, ПРИВЕДЕННЫЙ МОМЕНТ ИНЕРЦИИ, РЫЧАЖНЫЙ МЕХАНИЗМ, СИНТЕЗ МЕХАНИЗМА, СХЕМА УГЛА ДАВЛЕНИЯ, ЭВОЛЬВЕНТНОЕ ЗАЦЕПЛЕНИЕ
В данной пояснительной записке содержится динамический синтез рычажного механизма (определение кинематических передаточных функций скорости выходного и промежуточных звеньев, определение закона движения входного звена механизма под действием сил). Силовой анализ рычажного механизма (определение сил в кинематических парах механизма с учетом геометрии масс звеньев и их ускоренного движения). Синтез зубчатого механизма, который включает в себя расчет геометрии зацепления, и синтез планетарных и волновых зубчатых механизмов. Синтез кулачкового механизма (разработка циклограмм и тактограмм системы механизмов).
Реклама

Графическая часть включает:
– динамический синтез рычажного механизма – 1 лист А1;
–силовой анализ рычажного механизма – 1 лист А1;
– синтез зубчатых механизмов –1 лист А1;
–синтез кулачкового механизма –1 лист А1.
1
Динамический синтез рычажного механизма
Пресс: Процесс работы пресса осуществляется за период одного оборота кривошипа.
Принципы работы вертикального пресса.
Вертикальный пресс предназначен для получения изделий методом прессовки. Движение от электродвигателя передается кривошипу через планетарный редуктор и зубчатую передачу. Преобразование вращательного движения кривошипа в возвратно-поступательное движение поршня осуществляется шестизвенным рычажным кулисным механизмом, состоящим из кривошипа, шатуна, качающейся кулисы, кулисной тарелки, ползуна (поршня).. Смазывание механизмов пресса осуществляется плунжерным масляным насосом кулачкового типа. Кулачек закрепленный на одном валу с зубчатым колесом приводит в движение толкатель. Равномерное движение обеспечивает маховик.
Задачей динамического синтеза является определение постоянной определяющей составляющей 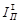 приведенного момента инерции, при котором колебания скорости звена приведения не превышает значений, определяемых заданным коэффициентом неравномерности движения приведенного момента инерции, при котором колебания скорости звена приведения не превышает значений, определяемых заданным коэффициентом неравномерности движения 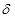 . .
Задачей динамического анализа является определение закона движения звена приведения в виде 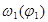 и и 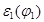 при полученном значении при полученном значении 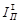 (куда входит искомый момент инерции маховика (куда входит искомый момент инерции маховика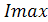 ). ).
Перечень звеньев механизма:
1 – кривошип; 2 – шатун; 3 – ползун.
Перечень кинематических пар:
0–1 – кинематическая пара 5-го класса, вращающаяся;
1–2 – кинематическая пара 5-го класса, вращающаяся;
2–3 – кинематическая пара 5-го класса, вращающаяся;
3–0 – кинематическая пара 5-го класса, поступательная;
Проведем структурный анализ механизма (рис 2.1) и установим класс заданного механизма. Число звеньев 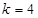 , число подвижных звеньев , число подвижных звеньев 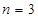 , число кинематических пар V класса , число кинематических пар V класса 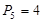 , степень подвижности: , степень подвижности:
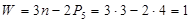
В
ходное звено 1 и стойка 0 образовывают механизм первого класса. Звенья 2 и 3 – группу Асура 2-го класса 2-го порядка 2-го вида. Данный механизм относится ко второму классу.
Структурная формула механизма будет иметь вид:
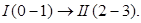
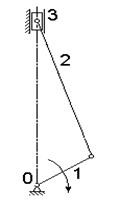
Рисунок 1.1 – структурный анализ механизма
Определение недостающих размеров
Определение длинны l1
и l2
, которые находятся из следующего равенства:
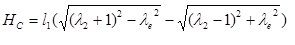 ,
(1. с.51) формула (2.12) ,
(1. с.51) формула (2.12)
подставив данные в формулу найдем 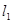 , ,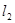 и е: и е:
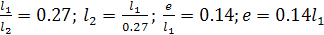
получаем 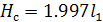
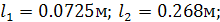 e=0.0105м e=0.0105м
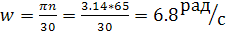
где 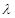 – отношение длины кривошипа к длине шатуна, – отношение длины кривошипа к длине шатуна,
Реклама

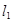 – длина кривошипа АВ, – длина кривошипа АВ,
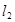 – длина шатуна ВС, – длина шатуна ВС,
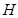 – ход ползуна, – ход ползуна,
ε – Отношение эксцентриситета к длине кривошипа.
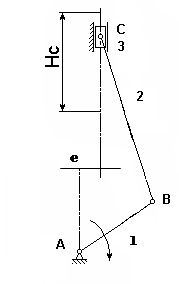
Рисунок 1.2
При графическом методе на чертеже изображаются звенья механизма в виде отрезков определенной длинны (в миллиметрах), соответствующих длине звеньев в ед. СИ, и кинематические пары связывающие звенья между собой в виде условных обозначений. Для построения планов положения механизма выбираем масштабный коэффициент длины:
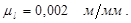
Длины отрезков на чертеже:
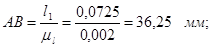 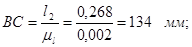 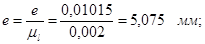
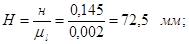 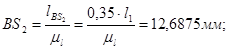
Основная система координат XOY связана со стойкой, а ее начало совпадает с осью вращения А входного звена 1. Обобщенной координатой φ1
механизма является угол поворота входного начального звена 1. Угол поворота считается положительным при отсчете от отрицательного направления оси ОХ по часовой стрелке, отрицательным – против часовой стрелки. Траекторию точки В звена 1 (окружность) делим на 12 равных частей.
1
.4 Описание построения планов аналогов скоростей
Необходимо построить планы аналогов скоростей для 12 положений механизма и определить длины отрезков, изображающих аналоги скоростей на планах.
Для построения планов скоростей воспользуемся векторными уравнениями. Скорость точки В (кривошипа):
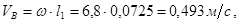
Масштабный коэффициент плана скоростей: 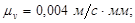
При построении планов аналогов скоростей длина отрезка pb будет равна:
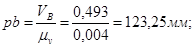
Для построения аналогов скорости точки С составим векторное уравнение и решим его графически:
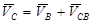 , , 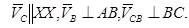
Строим аналог скорости центра масс – точки 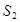 (отрезок (отрезок 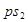 ). По теореме подобия получаем: ). По теореме подобия получаем:
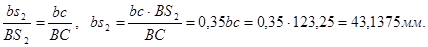
На планах аналогов скоростей измеряем длины соответствующих векторов. Полученные значения заносим в таблицу 1.1.
Таблица 1.1.
| № положения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| f (градусы) |
0 |
30 |
60 |
90 |
120 |
150 |
| pc (мм) |
0 |
36 |
59 |
61,6 |
47,5 |
26 |
3,5 |
| bс (мм) |
61,6 |
53 |
31,5 |
0 |
31 |
58,9 |
61 |
| bs2
(мм) |
21,6 |
18,6 |
11 |
0 |
10,9 |
20,6 |
21 |
| ps2
(мм) |
40 |
47,2 |
58,5 |
61,6 |
55 |
44 |
40 |
| Vc (м/c) |
0 |
0,288 |
0,472 |
0,493 |
0,38 |
0,208 |
0,028 |
| Vcb (м/с) |
0,493 |
0,424 |
0,252 |
0 |
0,248 |
0,471 |
0,488 |
| Vs2
(м/с) |
0,32 |
0,378 |
0,468 |
0,493 |
0,44 |
0,352 |
0,32 |
| № положения |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| f (градусы) |
180 |
210 |
240 |
270 |
300 |
330 |
| pc (мм) |
0 |
22 |
44,5 |
61,6 |
61,6 |
39 |
0 |
| cb (мм) |
61,6 |
54 |
32,2 |
0 |
31,5 |
54 |
61,6 |
| bs2
(мм) |
21,6 |
18,9 |
11,27 |
0 |
11 |
18,9 |
21,6 |
| ps2
(мм) |
40 |
44,5 |
53,6 |
61,6 |
59 |
48,5 |
40 |
| Vc (м/c) |
0 |
0,176 |
0,356 |
0,493 |
0,493 |
0,312 |
0 |
| Vcb (м/с) |
0,493 |
0,432 |
0,258 |
0 |
0,252 |
0,432 |
0,493 |
| Vs2
(м/с) |
0,32 |
0,356 |
0,429 |
0,493 |
0,472 |
0,388 |
0,32 |
1.
5 Определение приведенных моментов инерции
Найдем массы кривошипа, шатуна, поршня:
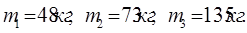
Определим величины приведенных моментов инерции для всех положений механизма и занесем полученные результаты в таблицу 1.2
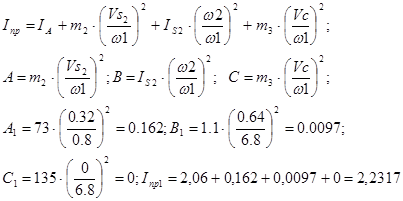
Таблица 1.2
| № пол |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| IA |
2,06 |
2,06 |
2,06 |
2,06 |
2,06 |
2,06 |
2,06 |
| A |
0,162 |
0,226 |
0,346 |
0,384 |
0,306 |
0,196 |
0,162 |
| B |
0,0097 |
0,007 |
0,003 |
0 |
0,0025 |
0,0088 |
0,009 |
| C |
0 |
0,242 |
0,65 |
0,71 |
0,421 |
0,126 |
0,002 |
| Iпр |
2,2317 |
2,535 |
3,059 |
3,154 |
2,79 |
2,391 |
2,233 |
| № пол |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| IА |
2,06 |
2,06 |
2,06 |
2,06 |
2,06 |
2,06 |
2,06 |
| А |
0,162 |
0,2 |
0,29 |
0,384 |
0,35 |
0,238 |
0,162 |
| В |
0,0097 |
0,0076 |
0,0027 |
0 |
0,003 |
0,007 |
0,0097 |
| С |
0 |
0,09 |
0,37 |
0,71 |
0,71 |
0,284 |
0 |
| Iпр |
2,232 |
2,358 |
2,723 |
3,154 |
3,123 |
2,589 |
2,2317 |
1.
6Определим силы сопротивления
Значение силы сопротивления найдем из индикаторной диаграммы.
Рассчитаем силы сопротивления для 14 положений механизма, полученные данные занесем в таблицу 1.3:
Таблица 1.3
| № пол |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Fс, кН |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| № пол |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| Fс, кН |
0 |
0,8 |
2 |
4 |
8,8 |
18,4 |
17,12 |
1.
7
Расчет приведенных моментов сил
Определим приведенный к валу кривошипа момент 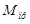 от сил сопротивления из условия равенства мощностей приведенного момента и сил. от сил сопротивления из условия равенства мощностей приведенного момента и сил.
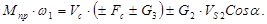 (1.1) (1.1)
Подставляя вместо скоростей отрезки, изображающие соответствующие скорости на планах скоростей, получим:
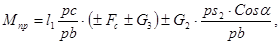 (1.2) (1.2)
где 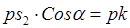 – проекция отрезка – проекция отрезка 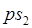 на направление силы тяжести звена ВС (на вертикаль). на направление силы тяжести звена ВС (на вертикаль).
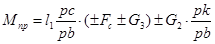
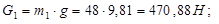 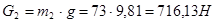
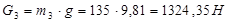 (1.3) (1.3)
При этом знак «+»будем ставить перед силами веса и силами сопротивлений тогда, когда эта сила является силой сопротивления; знак «-» перед движущими силами.
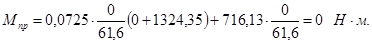
Определим значения 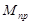 для каждого положения механизма, результаты занесем в таблицу 1.4. для каждого положения механизма, результаты занесем в таблицу 1.4.
Таблица 1.4
| № положения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Fc, Н |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| G2, H |
716,13 |
716,13 |
716,13 |
716,13 |
716,13 |
716,13 |
716,13 |
| G3, H |
1324,35 |
1324,35 |
1324,35 |
1324,35 |
1324,35 |
1324,35 |
1324,35 |
| Mпр, Н*м |
0 |
83,084 |
138,319 |
147,935 |
117,444 |
64,968 |
8,405 |
| № положения |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| Fc, Н |
0 |
800 |
2000 |
4000 |
8800 |
18400 |
17120 |
| G2, H |
716,13 |
716,13 |
716,13 |
716,13 |
716,13 |
716,13 |
716,13 |
| G3, H |
1324,35 |
1324,35 |
1324,35 |
1324,35 |
1324,35 |
1324,35 |
1324,35 |
| Mпр, Н*м |
0 |
-78,605 |
-215,915 |
-437,935 |
-781,215 |
-934,024 |
0 |
1.
8 Описание построения диаграмм работ, изменения кинетиской энергии, диаграммы Виттенбауэра
Методом графического интегрирования диаграммы приведенных моментов сил с полюсным расстоянием 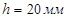 получаем диаграмму работ сил сопротивления получаем диаграмму работ сил сопротивления 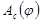 . .
Диаграмма работ движущих сил 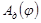 – прямая линия, соединяющая начало координат с последней точкой диаграммы – прямая линия, соединяющая начало координат с последней точкой диаграммы 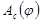 , так как момент движущих сил , так как момент движущих сил 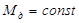 . .
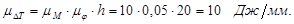 [1] стр. 135 (1.4) [1] стр. 135 (1.4)
В соответствии с выражением 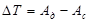 строим диаграмму избыточных работ (изменения кинетической энергии). строим диаграмму избыточных работ (изменения кинетической энергии).
Диаграмму Виттенбауэра строим при помощи диаграмм избыточных работ 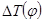 и приведенного момента инерции и приведенного момента инерции 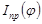 ,исключая общий параметр ,исключая общий параметр 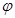 : : 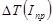 . .
1.
9 Определение момента инерции маховика
По заданному коэффициенту неравномерности вращения кривошипа и средней угловой скорости определяем углы 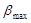 и и 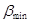 , образованных касательными к диаграмме Виттенбауэра с осью абсцисс. , образованных касательными к диаграмме Виттенбауэра с осью абсцисс.
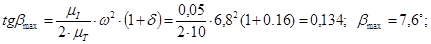 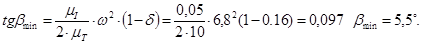 [1] стр. 137 [1] стр. 137
На диаграмме 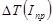 под углами под углами 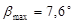 и и 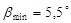 проводим касательные до пересечения с осью проводим касательные до пересечения с осью 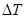 в точках K, L. Величина отрезка в точках K, L. Величина отрезка 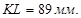
Момент инерции маховика находим по формуле:
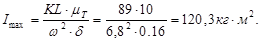 (1.5) (1.5)
Угловая скорость 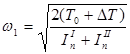 , [1] стр. 138 (1.6) , [1] стр. 138 (1.6)
где 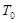 начальная кинетическая энергия (в начале цикла). начальная кинетическая энергия (в начале цикла).
На основании диаграммы Виттенбауэра:
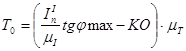 [1] стр. 138 (1.7) [1] стр. 138 (1.7)
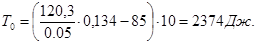
Результаты определения 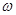 приведены в таблице 1.5, на основании которой построен график приведены в таблице 1.5, на основании которой построен график 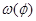 . Масштабный коэффициент: . Масштабный коэффициент:
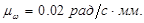
Для положения 0:
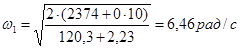
Таблица 1.5
| № положения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| To |
2374 |
2374 |
2374 |
2374 |
2374 |
2374 |
2374 |
| Iмах |
120,3 |
120,3 |
120,3 |
120,3 |
120,3 |
120,3 |
120,3 |
| Iмах+Iпрi |
122,53 |
122,83 |
123,36 |
123,45 |
123,09 |
122,69 |
122,53 |
| ∆Т |
0 |
103 |
240 |
391 |
550 |
692 |
791 |
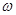 i i |
6,46 |
6,61 |
6,82 |
7,01 |
7,17 |
7,31 |
7,41 |
| № положения |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
| To |
3060 |
3060 |
3060 |
3060 |
3060 |
3060 |
2374 |
| Iмах |
33,5 |
33,5 |
33,5 |
33,5 |
33,5 |
33,5 |
120,3 |
| Iмах+Iпрi |
122,53 |
122,66 |
123,02 |
123,45 |
123,42 |
122,89 |
122,53 |
| ∆Т |
811 |
850 |
850 |
765 |
532 |
152 |
-30 |
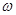 i i |
7,43 |
7,48 |
7,49 |
7,44 |
7,17 |
6,68 |
6,42 |
Определим среднюю угловую скорость:
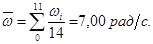
Определим погрешность вычислений.
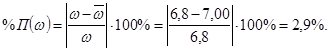
2
Динамический анализ рычажного механизма
Задание внешних сил, действующих на звенья механизма, позволяет найти закон движения начального звена в виде зависимостей ω1
(t) и ε1
(t). Следовательно, при силовом расчете механизмов законы движения начального звена и всех остальных подвижных звеньев механизма считаются заданными. Угловые ускорения звеньев и линейные ускорения центров масс, определяющие силы инерции звеньев при их движении, могут быть найдены методами кинематического анализа: с использованием аналитических, графических или численных методов исследования.
Знание сил в кинематических парах необходимо для расчетов на прочность, жесткость, износостойкость, надежность, для выбора типа и размеров подшипников, определения коэффициента полезного действия и др.
Решение задач динамического анализа механизма основано на принципе Даламбера.
Найдем угловое ускорение: Угловое ускорение 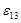 определяют из дифференциального уравнения движения: определяют из дифференциального уравнения движения:
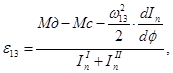 (2.1) (2.1)
где производная 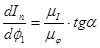 вычисляется по правилу графического дифференцирования. вычисляется по правилу графического дифференцирования.
Для положения 13:
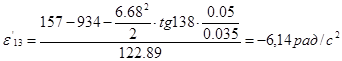
где 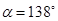 – угол наклона касательной к графику – угол наклона касательной к графику 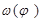 . .
 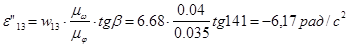 (2.2) (2.2)
где 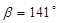 – угол наклона касательной к графику – угол наклона касательной к графику 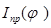 . .
Расхождение угловых ускорений составляет:
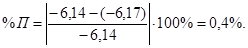
Для расчетов принимаем среднее значение:
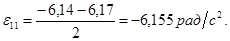
Используем графический метод построения планов скоростей и ускорений. Определяем скорость точки В:
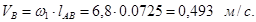 (2.3) (2.3)
Принимаем масштабный коэффициент 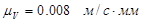 . Тогда отрезок, изображающий . Тогда отрезок, изображающий 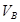 , равен: , равен:
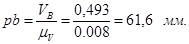 . .
Определяем скорость точки С:
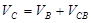 , ,
где 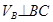 ; ; 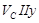 . .
Определяем ускорение точки В:
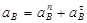 (2.4) (2.4)
где 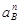 – нормальная составляющая ускорения точки В, направленная от В к А; – нормальная составляющая ускорения точки В, направленная от В к А; 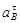 – тангенциальная составляющая ускорения точки В; – тангенциальная составляющая ускорения точки В;  сонаправлена с сонаправлена с 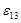 . .
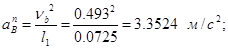 (2.5) (2.5)
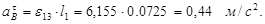 (2.6) (2.6)
Принимаем масштабный коэффициент 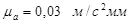 и находим отрезки, изображающие и находим отрезки, изображающие 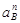 и и 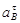 : :
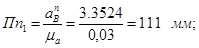 ; ;
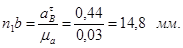 . .
Определяем ускорение точки С:
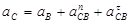 , ,
где 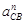 – направлена от точки С к точке В; – направлена от точки С к точке В; 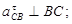 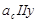 . .
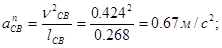 (2.7) (2.7)
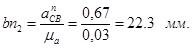 (2.8) (2.8)
По свойству подобия находим точку S2
:
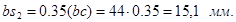 . .
Из плана ускорений находим:
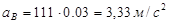
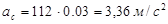
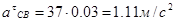
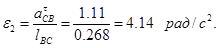 (2.9) (2.9)
Определяем силы и моменты сил инерции:
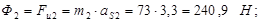 (2.10) (2.10)
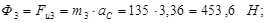 ; (2.11) ; (2.11)
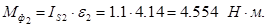 . (2.12) . (2.12)
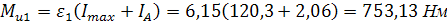 (2.13) (2.13)
Силы инерции направлены противоположено ускорениям центров масс, а моменты сил инерции – противоположено угловым ускорениям звеньев.
Отделяем от механизма статически определимую структурную группу (2,3). В точке С приложена реакция 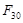 со стороны звена 0, а в точке В – реакция со стороны звена 0, а в точке В – реакция 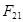 со стороны звена 1. со стороны звена 1. 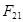 раскладываем на раскладываем на 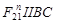 и и 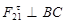 . . 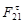 находим из уравнения: находим из уравнения:
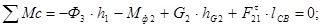 (2.15) (2.15)
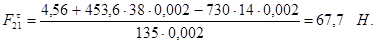
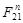 , , 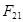 , , 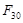 находим путем построения плана сил согласно уравнению равновесия группы: находим путем построения плана сил согласно уравнению равновесия группы:
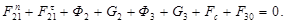 (2.14) (2.14)
Принимаем масштабный коэффициент 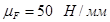 и находим отрезки, изображающие известные силы: и находим отрезки, изображающие известные силы:
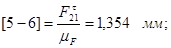 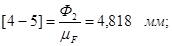
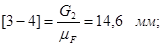 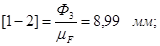
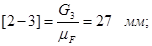 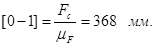
Из плана сил находим:
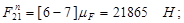
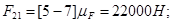
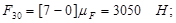
Рассматриваем кривошип 1. В точке В приложена известная реакция со стороны звена 2: 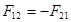 , а в точке А – реакция , а в точке А – реакция 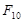 , которую находим путем построения плана сил согласно уравнению равновесия: , которую находим путем построения плана сил согласно уравнению равновесия:
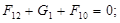 (2.15) (2.15)
Оценка точности расчетов
Находим относительную погрешность 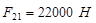 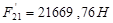
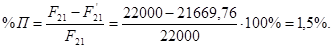
3
Синтез зубчатого зацепления
Исходные данные для открытой зубчатой передачи:
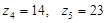 – числа зубьев колёс; – числа зубьев колёс;
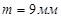 –модуль зубчатых колес; –модуль зубчатых колес;
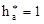 – коэффициент высоты головки зуба; – коэффициент высоты головки зуба;
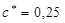 – коэффициент радиального зазора; – коэффициент радиального зазора;
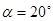 – угол профиля исходного контура. – угол профиля исходного контура.
Минимальное число зубьев:
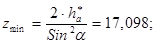
Коэффициенты смещения 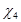 и и 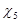 должны соответствовать условию: (При отсутствии подрезания зубьев.) должны соответствовать условию: (При отсутствии подрезания зубьев.)
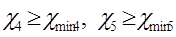 ; ;
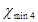 и и 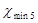 определяем по формуле: определяем по формуле:
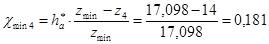 ; ;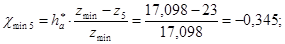
Выбираем из таблиц коэффициенты смещения 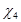 и и 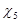 : :
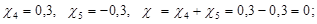
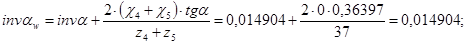
По таблице эвольвентных функций находим 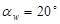 . .
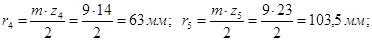
Радиусы основных окружностей
:
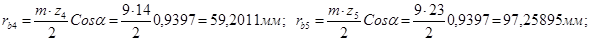
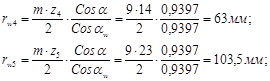
Коэффициенты воспринимаемого смещения:
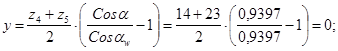
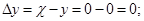
Межосевое расстояние передачи.
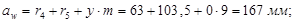
Радиусы окружностей впадин.
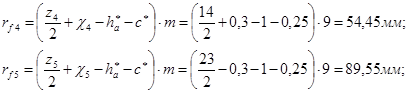
Радиусы окружностей вершин:
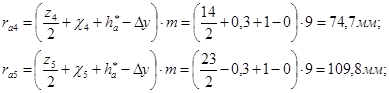
Высота зубьев колес:
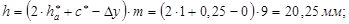
Окружной делительный шаг:
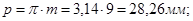
Угловой шаг.
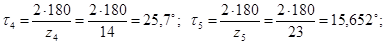
Толщины зубьев по окружности вершин:
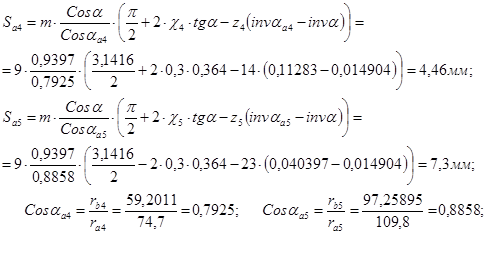
Толщины зубьев по дуге делительной окружности:
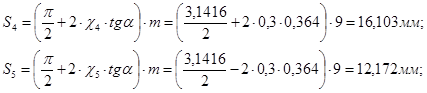
Толщины зубьев по основным окружностям:
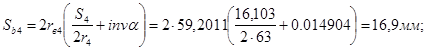 ; ;
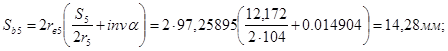 . .
Толщины зубьев по начальным окружностям:
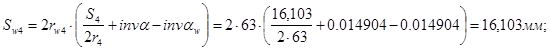
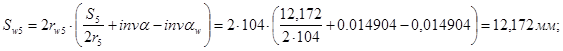
Радиусы кривизны эвольвент в нижних точках активных профилей:
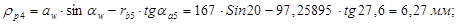 ; ;
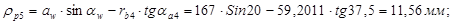
Радиусы кривизны эвольвент в граничных точках активных профилей:
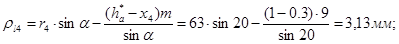
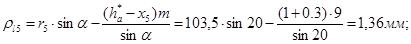
Коэффициент перекрытия:
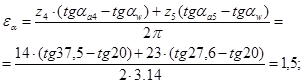
Проверка подрезания зубьев:
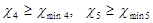
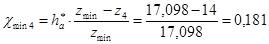 ; ;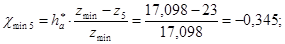
Т.к. 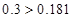 и и 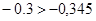 , подрезание отсутствует. , подрезание отсутствует.
Проверка отсутствия интерференции зубьев:
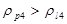 и и 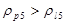 .Т.к. .Т.к. 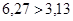 и и 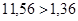 , то интерференция зубьев отсутствует. , то интерференция зубьев отсутствует.
Проверка плавности работы передачи:
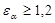 . Т.к. . Т.к. 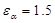 , то обеспечивается достаточная плавность. , то обеспечивается достаточная плавность.
Проверка заострения зубьев:
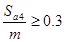 и и 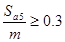
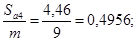 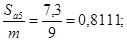
Т.к. 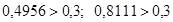 , то заострение зубьев отсутствует. , то заострение зубьев отсутствует.
При вычерчивании картины зацепления профилей используют длину шага между зубьями по делительным окружностям, равную  , основного шага по линии зацепления , основного шага по линии зацепления 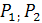 , равную , равную 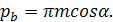 точки контакта профилей расположены на линии зацепления точки контакта профилей расположены на линии зацепления 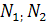 . .
В точках 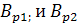 изображают пунктиром профили зубьев в момент начала и в момент окончания зацепления зубьев. изображают пунктиром профили зубьев в момент начала и в момент окончания зацепления зубьев.
Пользуясь схемой передачи, вычерченной в масштабе длин, измеряют длины отрезков и рассчитывают коэффициенты перекрытия 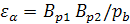 и удельного скольжения. и удельного скольжения.
Чертеж зацепления построен в масштабе 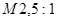
3.2 Геометрический синтез планетарного механизма
По заданному передаточному отношению 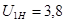 и числу сателлитов и числу сателлитов 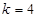 требуется определить числа зубьев колес требуется определить числа зубьев колес 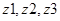 , исходя из условий соосности, сборки и соседства сателлитов, а также отсутствия подрезания и интерференции зубьев. , исходя из условий соосности, сборки и соседства сателлитов, а также отсутствия подрезания и интерференции зубьев.
Используем формулу Виллиса:
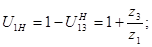 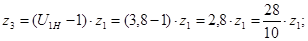
Из условия соосности колес 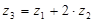 имеем: имеем:
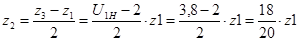 . .
Принимаем 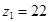 (при других значениях (при других значениях 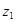 не будет выполняться условие сборки) и находим: не будет выполняться условие сборки) и находим:
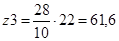 ; ; 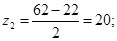 . .
Условие сборки:
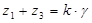 , где , где 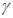 – любое целое число. – любое целое число.
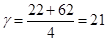 – условие выполняется т.к. – условие выполняется т.к. 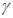 – целое число. – целое число.
Условие соседства сателлитов:
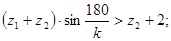
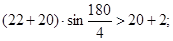 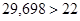 – условие выполняется. Т.к. – условие выполняется. Т.к. 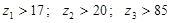 и и 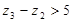 , то подрезания и интерференции зубьев не будет (в случае колес без смещения). , то подрезания и интерференции зубьев не будет (в случае колес без смещения).
Радиусы делительных окружностей:
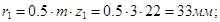
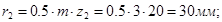
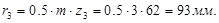 . .
Чертеж планетарного механизма зацепления построен в масштабе 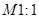
4
Синтез кулачкового механизма
Задачами синтеза кулачкового механизма являются:
1. Определение основных размеров механизма из условия ограниченности угла давления 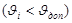 ; ;
2. Построение профиля кулачка, обеспечивающего заданный закон движения толкателя.
Фазовые углы поворота кулачка:
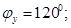 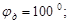 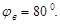 Аналог ускорения Аналог ускорения 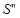 , аналог скорости , аналог скорости 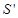 и перемещение и перемещение 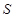 толкателя определяем аналитически для заданных законов движения. На фазе удаления закон №3, на фазе возвращения №1. толкателя определяем аналитически для заданных законов движения. На фазе удаления закон №3, на фазе возвращения №1.
№3 удаление - 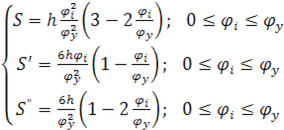 ; ;
№1 возвращение – 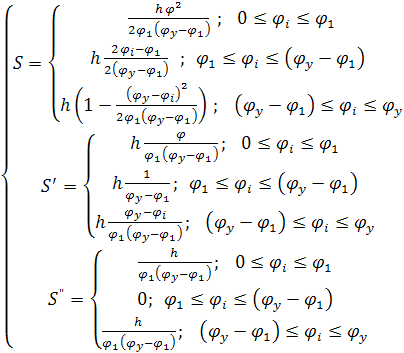 ; ;
Выбираем масштабы:
Данные, полученные в результате вычислений, занесем в таблицу 4.1.
Таблица 4.1 Фаза удаления
| I |
ji
|
Si
,мм |
S`,мм |
S``,мм |
| 1 |
0 |
0 |
0 |
0,0175 |
| 2 |
12 |
1,176 |
0,189 |
0,014 |
| 3 |
24 |
4,368 |
0,336 |
0,0105 |
| 4 |
36 |
9,072 |
0,441 |
0,007 |
| 5 |
48 |
14,784 |
0,504 |
0,0035 |
| 6 |
60 |
21 |
0,525 |
0 |
| 7 |
72 |
27,216 |
0,504 |
-0,0035 |
| 8 |
84 |
32,928 |
0,441 |
-0,007 |
| 9 |
96 |
37,632 |
0,336 |
-0,0105 |
| 10 |
108 |
40,824 |
0,189 |
-0,014 |
| 11 |
120 |
42 |
0 |
-0,0175 |
Фаза возвращения.
| 12 |
0 |
0 |
0 |
-0,0729 |
| 13 |
8 |
2,33 |
-0,583 |
-0,0729 |
| 14 |
16 |
7,00 |
-0,583 |
0 |
| 15 |
24 |
11,67 |
-0,583 |
0 |
| 16 |
32 |
16,33 |
-0,583 |
0 |
| 17 |
40 |
21,00 |
-0,583 |
0 |
| 18 |
48 |
25,67 |
-0,583 |
0 |
| 19 |
56 |
30,33 |
-0,583 |
0 |
| 20 |
64 |
35,00 |
-0,583 |
0 |
| 21 |
72 |
39,67 |
-0,583 |
0,0729 |
| 22 |
80 |
42,00 |
0 |
0,0729 |
Определим основные размеры Ro
и е кулачкового механизма по условию ограничения угла давления только на фазе удаления, так как высшая пара имеет силовое замыкание. Значения находим из диаграммы.
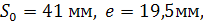 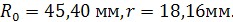
4.4 Построение профиля кулачка
Выбираем масштабный коэффициент: (1.5:1) по полученным значениям Ri
и αi
строим центровой профиль кулачка. Для этого в масштабе проводим окружность радиусами е=29,25 мм; Ro
=68,1 мм. Касательно к окружности радиусом е слева проводим линию движения толкателя уу. Соединив точку пересечения направляющей уу с окружностью радиусом R0
(точка В0
) с центром вращения кулачка (О1
), соответствующий началу удаления. От этого радиуса в направлении, противоположном вращению кулачка, отложим полярные углы αi
, на сторонах которых в масштабе отложим радиусы-векторы Ri
. Соединив плавной кривой, концы радиус-векторов, получим центровой профиль кулачка. Действительный профиль кулачка найдем как эквидистантою кривую, отстоящего от центрового профиля на расстоянии, равном радиусу ролика. Примем радиус ролика r=27мм.
Для расчета выбираем фазу возвращения, так как на этой фазе аналог ускорения толкателя имеет большее значение, чем на фазе удаления. Для закона изменения ускорения:
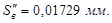
Предварительное натяжение:
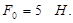
Предварительное натяжение пружины:
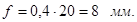 [1] стр. 69 [1] стр. 69
Сила инерции толкателя:
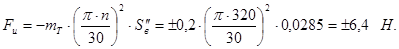 [1] стр. 69 [1] стр. 69
Из графика 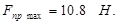
Жесткость вычисляем по формуле:
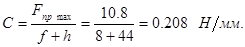 [1] стр. 69 [1] стр. 69
Заключение
В результате выполнения курсовой работы мы закрепили и обобщили знания и навыки, полученные при изучении дисциплины, научились применять на практике теорию курса (кинематику, динамику, синтез эвольвентного зацепления и синтез кулачкового механизма).
Выполняя курсовой проект по теории машин и механизмов, овладел навыками использования общих методов проектирования и исследования механизмов. Также овладел методами определения кинематических параметров механизмов, оценки сил, что действуют на отдельные звенья механизма, научился творчески оценивать сконструированный механизм с точки зрения его назначения – обеспечивать необходимые параметры движения звена.
Список использованных источников
1. Попов С.А. Курсовое проектирование по теории механизмов и механике машин. - М.: Высшая школа, 1986.
2. Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин. - М.: Высшая школа, 1999.
3. Марголин Ш.Ф. Теория механизмов и машин. - Мин.: Высшая школа, 1968.
4. Курсовое проектирование по теории механизмов и машин. / Под ред. Девойно Г.Н. - Мин.: Высшая школа, 1986.
|




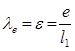 ;
;

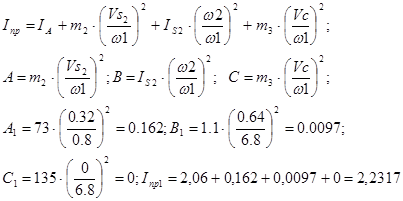
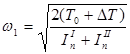 , [1] стр. 138 (1.6)
, [1] стр. 138 (1.6)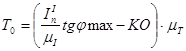 [1] стр. 138 (1.7)
[1] стр. 138 (1.7)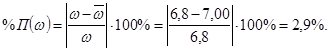
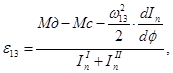 (2.1)
(2.1)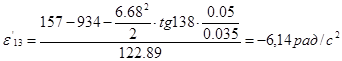
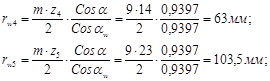
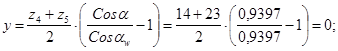
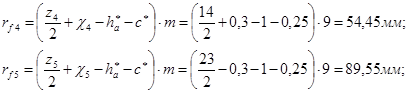
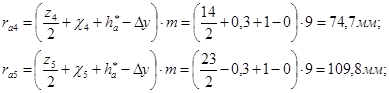
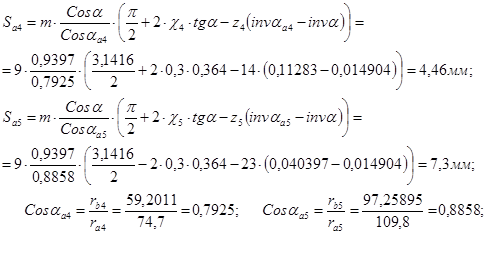
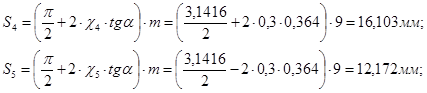
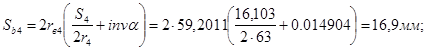 ;
;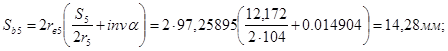 .
.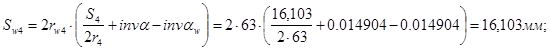
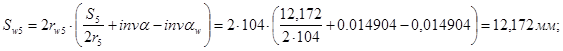
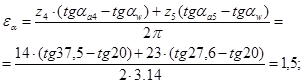
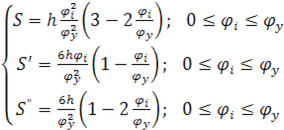 ;
;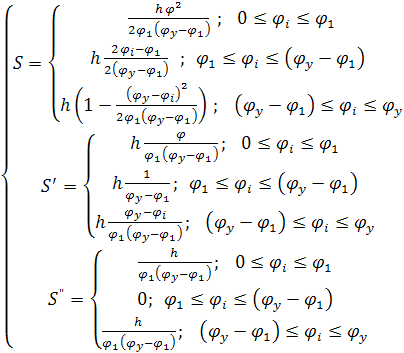 ;
;