| Оглавление.
Введение…………………………………………………………………2
Глава 1. Теоретическая часть…………………………………………4
1.1. Квадратичная форма и ее матрица………………………………4
1.2. Преобразование квадратичной формы при линейном однородном преобразовании переменных………………………………8
1.3. Приведение действительной квадратичной формы к нормальному виду…………………………………………………………9
1.4. Закон инерции квадратичных форм……………………………12
1.5. Знакоопределенные квадратичные формы……………………13
1.6. Приведение квадратичной формы к каноническому виду ортогональным преобразованием переменных……………………15
1.7. Упрощение уравнений фигур второго порядка на плоскости и в пространстве……………………………………………………..15
Глава 2. Практическая часть…………………………………………23
Список использованной литературы…………………………………25
Введение.
Арифметическая теория квадратичных форм берет свое начало с утверждения Ферма о представимости простых чисел суммой двух квадратов.
Теория квадратичных форм впервые была развита французским математиком Лагранжем, которому принадлежат многие идеи в этой теории, в частности, он ввел важное понятие приведенной формы, с помощью которого им была доказана конечность числа классов бинарных квадратичных форм заданного дискриминанта. Затем эта теория была значительно расширена Гауссом, который ввел много новых понятий, на основе которых ему удалось получить доказательства трудных и глубоких теорем теории чисел, ускользавших от его предшественников в этой области
Изучение основ теории билинейных и квадратичных форм вызывает ряд трудностей методического характера, обусловленных существованием нескольких различных подходов к построению этой теории. Принятое изложение, основанное на теории унитарных и евклидовых пространств и содержит единый подход к изучению симметричных и эрмитовых форм.
При изучении квадратичных форм необходимо знание классических понятий теории унитарных и евклидовых пространств и основных свойств самосопряженных и унитарных (ортогональных) линейных операторов. Общими обозначениями являются: P – основное поле, под которым мы будем понимать поле комплексных чисел C или поле действительных чисел R. α - комплексное число, сопряженное к комплексному числу α ( α= α . α . R); |α| - модуль комплексного числа α. L - линейное пространство над полем P. В случае, когда размерность линейного пространства L равна n (L = Ln) будем считать L унитарным (при P = C ) или евклидовым (при P = R ) пространством, так как на любом конечном пространстве Ln над полем C или R можно определить скалярное произведение. Для любых векторов x, y . Ln (x, y) обозначает их скалярное произведение. Остальные обозначения или являются общепринятыми в линейной алгебре.
Реклама

Целью курсовой работы является рассмотрение квадратичной формы и ее свойств.
Перейдем теперь к краткой характеристике содержания курсовой работы, посвященной некоторым вопросам теории неопределенных бинарных квадратичных форм.
В теоретической части работы приводятся предварительные общие сведения квадратичных формах и ее свойств.
В практической части курсовой работы представляется решение задач по заданной теме.
Глава 1. Теоретическая часть.
1.1. Квадратичная форма и ее матрица.
Квадратичной формой называется функция B(x) = A(x,x) из линейного пространства L над произвольным полем F характеристики не 2 в поле F, которая получается из билинейной формы A(x,y) при x = y.
При фиксированном базисе в L квадратичная форма 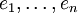 имеет вид имеет вид 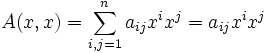 (по соглашению Эйнштейна), где , а aij =aji. (по соглашению Эйнштейна), где , а aij =aji.
Квадратичной формой f (x1
,x2
…,xn
) п действительных переменных (x1
,x2
…,xn
) называется сумма вида:
 (1.1) (1.1)
или f(x1,
x2,…
xn
) = ∑i
=1
∑ j
=1
aij
xi
xj
,
(1.2), где aij
- некоторые числа, называемые коэффициентами.
Не ограничивая общности, можно считать, что aij
=
aji
.
Квадратичная форма называется действительной или комплексной в зависимости от того, являются ли ее коэффициенты соответственно действительными или комплексными числами. Будем рассматривать действительные квадратичные формы.
Квадратичная форма обладает следующими свойствами:
1) Симметричную билинейную форму A(x,y), называют полярной квадратичной форме A(x,x). Матрица билинейной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.
2) Если матрица квадратичной формы имеет полный ранг, то квадратичную форму называют невырожденной, иначе - вырожденной.
3) Квадратичная форма A(x,x) называется положительно (отрицательно) определённой, если для любого x≠ 0 A(x,x) > 0 (A(x,x) < 0). Положительно определённые и отрицательно определённые формы называются знакоопределёнными.
Реклама

Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
4) Квадратичная форма A(x,x) называется знакопеременной, если она принимает как положительные, так и отрицательные значения.
5) Квадратичная форма A(x,x) называется квазизнакоопределённой, если 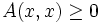 , но форма , но форма 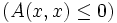 не является знакоопределённой. не является знакоопределённой.
Для приведения квадратичной формы к каноническому виду используется метод Лагранжа. Метод приведения квадратичной формы к каноническому виду, указанный в 1759 году Лагранжем.
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть 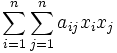 есть данная квадратичная форма. Возможны два случая: есть данная квадратичная форма. Возможны два случая:
- хотя бы один из коэффициентов aii
при квадратах отличен от нуля. Не нарушая общности, будем считать a11
≠0 (этого всегда можно добиться соответствующей перенумерацией переменных);
- все коэффициенты aii
= 0,i = 1,2,...,n, но есть коэффициент 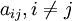 , отличный от нуля (для определённости пусть будет ) a12
≠0. , отличный от нуля (для определённости пусть будет ) a12
≠0.
В первом случае преобразуем квадратичную форму следующим образом: 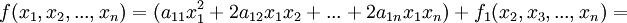
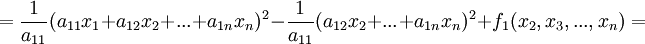
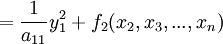 , где y1
= a11
x1
+ a12
x2
+ ... + a1n
xn
, а через f2
(x2
, x3
,...,xn
) обозначены все остальные слагаемые. f2
(x2,...,xn
) представляет собой квадратичную форму от n-1 переменных x2
, x3
,...,xn
. С ней поступают аналогичным образом и так далее. Заметим, что , где y1
= a11
x1
+ a12
x2
+ ... + a1n
xn
, а через f2
(x2
, x3
,...,xn
) обозначены все остальные слагаемые. f2
(x2,...,xn
) представляет собой квадратичную форму от n-1 переменных x2
, x3
,...,xn
. С ней поступают аналогичным образом и так далее. Заметим, что 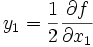 . .
Второй случай заменой переменных x1
= y1
+ y2
, x2
= y1
− y2
, x3
= y3
,...,xn
= yn
сводится к первому.
Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (1.1) соответствует единственная симметрическая матрица
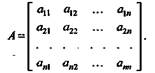 (1.3) (1.3)
И наоборот, всякой симметрической матрице (1.3) соответствует единственная квадратичная форма с точностью до обозначения переменных.
Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма n переменных называется невырожденной, если ее матрица невырожденная, т. е. r = п, и вырожденной, если r< п. При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц удобно решать системы линейных уравнений, выполнять многие операции с векторами, решать различные задачи компьютерной графики и другие инженерные задачи.
Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество п столбцов. Числа т и п называются порядками матрицы. В случае, если т = п, матрица называется квадратной, а число m = n -- ее порядком.
В дальнейшем для записи матриц будут применяться либо сдвоенные черточки, либо круглые скобки
Квадратичную форму (1.1) п переменных х1
, х2
,...,хn
можно записать в матричном виде. Действительно, если Х- матрица-столбец из переменных (x1
,x2
…,xn
), XT
-
матрица, полученная транспонированием матрицы X, т.е. матрица-строка из тех же переменных, то f (x1
,x2
…,xn
)= XT
AX (1.4), А определяется формулой (1.3).
Пример 1.
Пусть e1
, ..., en
— базис в L. И пусть для вектора x из L задано разложение x = x1
·e1
+x2
·e2
+ ...+ xn
· en
. Тогда для квадратичной формы k(x) справедливо представление
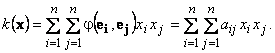 Здесь φ(ei
, ej
) — значение полярной для k(x) билинейной формы φ(x , y). Матрица A = {aij
} называется матрицей квадратичной формы. Определённая таким образом матрица квадратичной формы является симметричной матрицей. Пусть k(x) = x12
+ x22
— квадратичная форма в пространстве R2
. Пусть e1
= (1, 0), e2
= (0, 1) — базис в R2
. Вычислим матрицу A квадратичной формы. Поскольку симметричная билинейная форма φ(x, y) = (x, y) — полярная для квадратичной формы k(x) = φ(x, x ) то матрица A квадратичной формы совпадает с матрицей Φ билинейной формы φ(x , y): Здесь φ(ei
, ej
) — значение полярной для k(x) билинейной формы φ(x , y). Матрица A = {aij
} называется матрицей квадратичной формы. Определённая таким образом матрица квадратичной формы является симметричной матрицей. Пусть k(x) = x12
+ x22
— квадратичная форма в пространстве R2
. Пусть e1
= (1, 0), e2
= (0, 1) — базис в R2
. Вычислим матрицу A квадратичной формы. Поскольку симметричная билинейная форма φ(x, y) = (x, y) — полярная для квадратичной формы k(x) = φ(x, x ) то матрица A квадратичной формы совпадает с матрицей Φ билинейной формы φ(x , y):
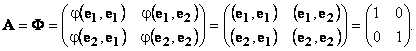
Проверим. Для этого подставим матрицу A в матричное представление квадратичной формы k(x)=xT·A·x:
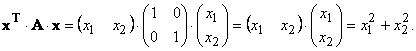
Матрица квадратичной формы вычислена, верно.
Пусть k(x) = 3x12
− 2x2
x1
+ 3x22
— квадратичная форма в пространстве R2
. Пусть e1
= (1, 0), e2
= (0, 1) — базис в R2. Вычислим матрицу A квадратичной формы. Поскольку симметричная билинейная форма φ(x, y) = φ(x1
, x2
, y1
, y2
) = 3x1
y1
− x2
y1
− x1
y2
+ 3x2
y2
— полярная для квадратичной формы k(x) = 3x12
− 2x2
x1
+ 3x22
, k(x) = φ(x, x ) то матрица A квадратичной формы совпадает с матрицей Φ билинейной формы φ(x, y):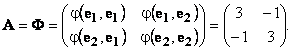
Проверим. Для этого подставим матрицу A в матричное представление квадратичной формы k(x)=xT
·A·x:
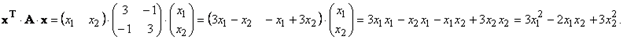
Матрица квадратичной формы вычислена, верно.
1.2. Преобразование квадратичной формы при линейном однородном преобразовании переменных.
Рассмотрим квадратичную форму (1.1). Перейдем к новым переменным y1
, y2
….yn
по формулам
 (1.5) (1.5)
или в матричном виде X=BY (1.6), где 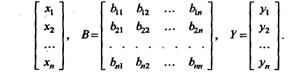 (1.7). В квадратичной форме (1.1) вместо (x1
,x2
…,xn
) подставим их выражения через y1
, y2
….yn
определяемые формулами (1.5), получим квадратичную форму φ (y1
, y2
….yn
) п переменных с некоторой матрицей С. В этом случае говорят, что квадратичная форма f(x1,
x2,…
xn
) переводится в квадратичную форму φ (y1
, y2
….yn
) линейным однородным преобразованием (1.5). Линейное однородное преобразование (1.6) называется невырожденным, если det B≠0. (1.7). В квадратичной форме (1.1) вместо (x1
,x2
…,xn
) подставим их выражения через y1
, y2
….yn
определяемые формулами (1.5), получим квадратичную форму φ (y1
, y2
….yn
) п переменных с некоторой матрицей С. В этом случае говорят, что квадратичная форма f(x1,
x2,…
xn
) переводится в квадратичную форму φ (y1
, y2
….yn
) линейным однородным преобразованием (1.5). Линейное однородное преобразование (1.6) называется невырожденным, если det B≠0.
Две квадратичные формы называются конгруэнтными, если существует невырожденное линейное однородное преобразование, переводящее одну форму в другую. Если f (x1
,x2
…,xn
) и φ (y1
, y2
….yn
) конгруэнтны, то будем писать f (x1
,x2
…,xn
) ~ φ (y1
, y2
….yn
). Свойства конгруэнтности квадратичных форм:
1. f (x1
,x2
…,xn
) ~ φ (y1
, y2
….yn
).
2. Если f (x1
,x2
…,xn
) ~ φ (y1
, y2
….yn
), φ (y1
, y2
….yn
)~ψ(z1
, z2
…zn
)
Теорема 1. Квадратичная форма f (x1
,x2
…,xn
) с матрицей А линейным однородным преобразованием Х = ВУ переводится в квадратичную форму φ (y1
, y2
….yn
) с матрицей С=ВT
АВ.
Следствие 1. Определители матриц конгруэнтных невырожденных действительных квадратичных форм имеют одинаковые знаки.
Следствие 2. Конгруэнтные квадратичные формы имеют одинаковые ранги.
1.3. Приведение действительной квадратичной формы к нормальному виду.
Квадратичная форма f (x1
,x2
…,xn
) называется канонической, если она не содержит произведений различных переменных, т. е. 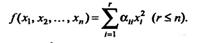 (1.8). Каноническая квадратная форма называется нормальной (или имеет нормальный вид), если | an
| = 1 ( i= 1, 2, . . . , r), т. е. отличные от нуля коэффициенты при квадратах переменных равны +1 или —1. (1.8). Каноническая квадратная форма называется нормальной (или имеет нормальный вид), если | an
| = 1 ( i= 1, 2, . . . , r), т. е. отличные от нуля коэффициенты при квадратах переменных равны +1 или —1.
Например, квадратичная форма f (x1
,x2
…,xn
) = 6x2
1
+4x2
3
– 3x2
4
, для которой a11
=6, a22
=0, a33
= 4, a44
= -3, имеет канонический вид; квадратная форма f (x1
, x2,
x3,
x4
) = x2
1
- - x2
3
+ x2
4
является нормальной, так как a11
=1, a22
=0, a33
= - 1, a44
= 1.
Теорема 2. Любая квадратичная форма некоторым невырожденным линейным преобразованием может быть приведена к каноническому виду
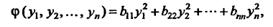 , где y1
, y2
….yn
– новые переменные. , где y1
, y2
….yn
– новые переменные.
Некоторые из коэффициентов bij
могут оказаться равными нулю; число отличных от нуля коэффициентов в этой формуле равно рангу r матрицы квадратичной формы φ. Теорема 3. Любую действительную квадратичную форму линейным невырожденным преобразованием можно привести к нормальному виду 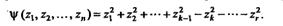 Число входящих сюда квадратов равно рангу формы. Число входящих сюда квадратов равно рангу формы.
Пример 1. Привести к каноническому виду квадратичную форму Ф(х1
, х2
) = 27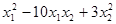 . Коэффициенты: а11
= 27, а12
= 5, а22
= 3. . Коэффициенты: а11
= 27, а12
= 5, а22
= 3.
Составим характеристическое уравнение: 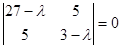 ; ;
(27 - l)(3 - l) – 25 = 0
l2
- 30l + 56 = 0
l1
= 2; l2
= 28;
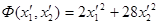
Пример 2. Привести к каноническому виду уравнение второго порядка: 17x2
+ 12xy + 8y2
– 20 = 0. Коэффициенты а11
= 17, а12
= 6, а22
= 8. А = 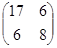 . Составим характеристическое уравнение: . Составим характеристическое уравнение: 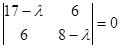
(17 - l)(8 - l) - 36 = 0
136 - 8l - 17l + l2
– 36 = 0
l2
- 25l + 100 = 0 l1
= 5, l2
= 20.
Итого: 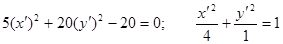 - каноническое уравнение эллипса. - каноническое уравнение эллипса.
Пример 3. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график. 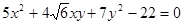
Решение: Составим характеристическое уравнение квадратичной формы 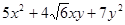 :при :при 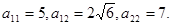
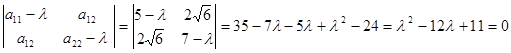
Решив это уравнение, получим l1
= 1, l2
= 11.
Найдем координаты собственных векторов:
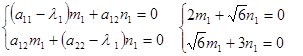 полагая m1
= 1, получим n1
= полагая m1
= 1, получим n1
= 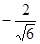
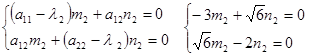 полагая m2
= 1, получим n2
= полагая m2
= 1, получим n2
= 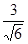
Собственные векторы: 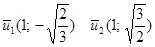
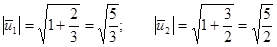
Находим координаты единичных векторов нового базиса.
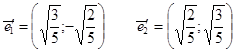
Имеем следующее уравнение линии в новой системе координат: 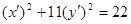
Каноническое уравнение линии в новой системе координат будет иметь вид:
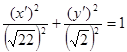

1.4. Закон инерции квадратичных форм.
Закон инерции квадратичных форм выражает:
Теорема 4. Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная действительная квадратичная форма невырожденным действительным линейным преобразованием, не зависит от выбора преобразования.
Число положительных квадратов в нормальной форме, к которой приводится данная действительная квадратичная форма, называют положительным индексом инерции этой формы, число отрицательных квадратов - отрицательным индексом инерции, разность между положительным и отрицательным индексами инерции - сигнатурой формы f. Если известен ранг формы, то задание любого из трех указанных выше чисел определяет два других.
Теорема 5. Две действительные квадратичные формы от n переменных тогда и только тогда конгруэнтны, когда они имеют одинаковые ранги и одинаковые сигнатуры.
Пусть k(x) = 3x12 − 2x2x1+ 3x22— квадратичная форма в пространствеR2. И пусть e1= (1, 0), e2= (0, 1) — базис в R2. Марица A квадратичной формы в этом базисе имеет вид: 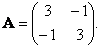 Найдём канонический базис квадратичной формы — собственный базис матрицы A и приведём её к диагональному виду: Найдём канонический базис квадратичной формы — собственный базис матрицы A и приведём её к диагональному виду:

Имеем: E1, E2 — канонический базис квадратичной формы. Канонический вид квадратичной формы в этом базисе k(y) = 4y12 + 2y22. Числа 4, 2 — канонические коэффициенты квадратичной формы. Положительный индекс инерции квадратичной формы равен 2. Отрицательный индекс инерции квадратичной формы равен 0. Сигнатура квадратичной формы равна 2 − 0 = 2. Ранг квадратичной формы равен 2.
1.5. Знакоопределенные квадратичные формы.
Действительная квадратичная форма f (x1
,x2
…,xn
) называется положительно-определенной, если она приводится к нормальному виду, состоящему из п положительных квадратов: f (x1
,x2
…,xn
) ~ φ (y1
, y2
….yn
), где 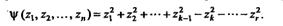 (1.9) , т. е. если ранг и положительный индекс инерции равны числу неизвестных. (1.9) , т. е. если ранг и положительный индекс инерции равны числу неизвестных.
Систему значений x1
,x2
…,xn
назовем нулевой, если x1
= х2
= ... = xn
=0, и ненулевой, если хотя бы одно из них отлично от нуля.
Теорема 6. Действительная квадратичная форма f (x1
,x2
…,xn
) является положительно-определенной тогда и только тогда, когда она принимает положительные значения при любой ненулевой системе значений переменных x1
, x2
…,xn
. Пусть дана квадратичная форма f (x1
,x2
…,xn
) с матрицей А = (ау
). Главными минорами квадратичной формы f называются миноры 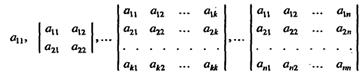 , т. е. миноры порядка 1, 2, ... , п матрицы А, расположенные в левом верхнем углу; последний из них совпадает с определителем матрицы. , т. е. миноры порядка 1, 2, ... , п матрицы А, расположенные в левом верхнем углу; последний из них совпадает с определителем матрицы.
Теорема 7. Квадратичная форма f (x1
,x2
…,xn
) с действительной
матрицей является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны.
Действительная квадратичная форма называется отрицательно-определенной, если она является невырожденной и приводится к нормальному виду, содержащему только отрицательные квадраты всех переменных; эту форму можно привести к виду:
φ (y1
, y2
….yn
)= -y2
1
– y2
2
-…- y2
n
(1.10).
Теорема 8. Квадратичная форма является отрицательно-определенной тогда и только тогда, когда ее главные миноры четного порядка положительны, а нечетного - отрицательны.
Положительно-определенные и отрицательно-определенные квадратичные формы называются знакоопределенными квадратичными формами.
Вырожденные квадратичные формы, нормальный вид которых состоит из квадратов одного знака, называются полуопределенными. Неопределенными называются квадратичные формы, нормальный вид которых содержит как положительные, так и отрицательные квадраты переменных.
Пример. Доказать, что квадратичная форма f (x1
, x2
, x3
)
= 6x2
1
+ 5х2
2
+ 7х2
3
- 4х1
х2
+ 4х1
x3
положительно-определенная.
Запишем матрицу A этой квадратичной формы и определитель матрицы А: 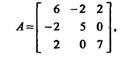 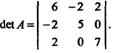
Так как главные миноры матрицы a11
=6, 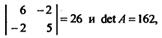 все положительны, то данная квадратичная форма является положительно-определенной. все положительны, то данная квадратичная форма является положительно-определенной.
1.6. Приведение квадратичной формы к каноническому виду ортогональным преобразованием переменных.
Теорема 9. Если существует ортогональное преобразование с матрицей С, приводящее действительную квадратичную форму f (x1
,x2
…,xn
) к каноническому виду:
φ (y1
, y2
….yn
)= λ1
y2
1
+λ2
y2
2
+λn
y2
n
(1.11),
то λ1,
λ2,….
λn
— характеристические числа матрицы А квадратичной формы f.
Теорема 10. Для любой действительной квадратичной формы существует ортогональное преобразование, приводящее ее к каноническому виду.
Теорема 11. Для любой действительной симметрической матрицы А существует такая ортогональная матрица Т, что Т-1
АТ - диагональная матрица.
С помощью матрицы В записываем искомое ортогональное преобразование x1
= √3/5 y1
+ √2/5 y2
, x1
= 1/√5(√3y1
+ √2y2
) или x2
= √2/5 y1
+ √3/5 y2
, x2
= 1/√5 (- √2y1
+ √3y2
).
Это преобразование приводит данную квадратичную форму к каноническому виду φ (y1
, y2
) = y2
1
+ 11y2
2
.
1.7. Упрощение уравнений фигур второго порядка на плоскости и в пространстве
  
   
Глава 2. Практическая часть.
Задание 1.
Привести к каноническому виду уравнение линии в квадратичной форме.
Задание 2
. Какую поверхность определяет уравнение 6x2
+5y2
+7z2
– 4xy+4xz=18?
Решение задания № 1.
Составим характеристическое уравнение квадратичной формы 6x2
+ 2√5xy + 2y2
– 21=0, при a11
=6, a12
=√5, a22
=2.
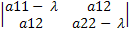 = = 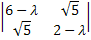 = (6 – λ)(2 – λ) -5 = 12 – 6λ – 2λ + λ2
– 5=λ2
- 8λ+ 7. = (6 – λ)(2 – λ) -5 = 12 – 6λ – 2λ + λ2
– 5=λ2
- 8λ+ 7.
Находим корни этого уравнения, λ1
= 7, λ2
= 1.
Найдем координаты собственных векторов:
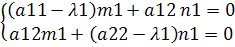
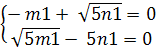 Полагая m1
= 1, получим n1
= 1/√5 Полагая m1
= 1, получим n1
= 1/√5
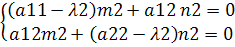
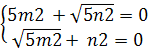 Полагая m2
= 1, получим n2
= - √5 Полагая m2
= 1, получим n2
= - √5
Собственные векторы: U1
= (1;1/√5) и u2
= (1; - √5), [u1
] = √6 и [u2
] = 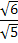
Находим координаты единичных векторов нового базиса,
е1
= (√5/√6; - √1/√6) и е2
= (√1/√6; √5/√6).
Имеем следующее уравнение линии в новой системе координат:
(xt
)2
+3(yt
)2
= 21
Каноническое уравнение линии в новой системе координат будет иметь вид: xt
2
/ 21 + yt
2
/ =1.
Ответ: Каноническое уравнение линии в новой системе координат будет иметь вид: xt
2
/ 21 + yt
2
/ =1.
Решение задания № 2.

Ответ: уравнение определяет эллипсоид с полуосями, а =√6, b =√3, c = √2.
Список использованной литературы
1) Гусак А. А., Гусак Г. М., Бричникова Е. А. Справочник по высшей математике. – М.:ТетраСистемс, 1999- 640 с.
2) Малугин В. А. Математика для экономистов: Линейная алгебра. Курс лекций. – М.: Эксмо, 2006- 224 с.
3) Данко П. Е. Высшая математика в упражнениях и задач. Ч.1. – М.: Высш. Шк., 2003.
4) Крутицкая Н. Ч., Шишкин А. А. Линейная алгебра в вопросах и задачах: Учеб. Пособие для вузов. – М.:Высш. шк.,1985.
5) Виноградов И. М. Элементы высшей математики. (Аналитическая геометрия. Дифференциальное исчисление. Основы теории чисел). Учебник для вузов. – М.: Высш. шк., 1999.
6) Щипачев В. С. Высшая математика: Учебник для вузов. – Высш. шк., 2005.
7) В.А.Ильин, Э.Г.Позняк. Линейная алгебра. М.: Наука, 1999.
8) И.В.Проскуряков. Сборник задач по линейной алгебре. М.: Наука, 2000.
9) В.Л.Камынин, Н.В.Шолохов. Элементы теории групп. М.:МИФИ, 1997.
|