Вологодская государственная молочнохозяйственная
академия имени Н.В. Верещагина
Кафедра сельскохозяйственных машин и ЭМТП
Расчетно-графическое задание
Расчет триерного цилиндра
Вариант 1
Выполнил
студент 342группы
Девятовский А.С.
Принял
Пустынный Д.А.
Вологда-Молочное
2010
Дано:
Подача материала q= 0,2кг/с
Диаметр ячеек d = 5 мм
Плотность зернового материала 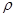 = 0,74 кг/дм3 = 0,74 кг/дм3
Показатель кинематического режима работы триера k= 0,4
Доля коротких примесей bK
= 10 %
Углы трения зерен о поверхность ячеек 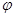 min
= 20 min
= 20
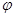 max
= 300 max
= 300
Угол трения зерен о поверхность триерного цилиндра 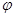 = 190 = 190
Угол, определяющий форму ячеек 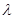 = = 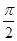 =
900 =
900
1.ОПРЕДЕЛИТЬ ДЛИНУ И ДИАМЕТР ТРИЕРА
Для определения диаметра триера воспользуемся формулой:
L2
R=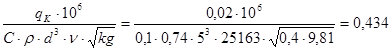
где:
qk
-
относительное количество коротких (длинных) зерен:
L- длина триерного цилиндра, м;
R- радиус цилиндра, м;
Относительное количество коротких (длинных) зерен:
qk
=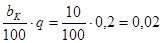
где:
bK
- доля коротких примесей(bK
=10 %)
q- подача материала (q=0,2 кг/с)
С - коэффициент, зависящий от условий работы и от зернового материала, С = 10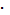 10-2
м-3/2
=0,01 м-3/2-
при выделении коротких примесей (овсюжный триер). 10-2
м-3/2
=0,01 м-3/2-
при выделении коротких примесей (овсюжный триер).
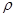 - плотность зернового материала; - плотность зернового материала;
d- диаметр ячейки, мм;
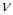 - число ячеек на 1 м2 - число ячеек на 1 м2
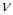 = = 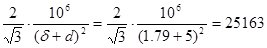
где:
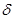 - ширина перемычек между ячейками, - ширина перемычек между ячейками, 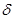 =1,79мм =1,79мм
k- показатель кинематического режима триера;
g- ускорение свободного падения.
Найдем производительность триера:
QР
= qB
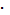 B B
QР
= 180 10 = 1800 кг/ч 10 = 1800 кг/ч
Qтр
= QР
 (1- Р0
) (1- Р0
)
Qтр
= 1800 (1-0,4) = 1080 кг/ч (1-0,4) = 1080 кг/ч
Примем диаметр триера D= 400 мм.
L= 1,11 м.
Зная производительность триера, площадь ячеистой поверхности определяется по формуле:
Fmax
= 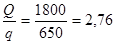
Fmin
= 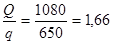
По найденной площади ячеистой поверхности и выбранному диаметру D определим длину триера:
Lmax
=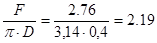
Lmin
=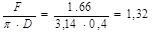
Примем длину триера L= 1,6 м.
2. Определить параметры, характеризующие поведение зерна в триере
Предельное положение зерна, находящегося в состоянии относительного покоя:
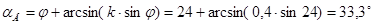
Определим нижнюю и верхнюю границы выпадения зерен из ячейки:
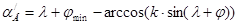
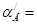 90+2 - arccos(0,4 90+2 - arccos(0,4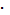 sin(90+2)) = 23,90 sin(90+2)) = 23,90

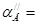 90+30 - arccos(0,4 90+30 - arccos(0,4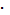 sin(90+30)) = 50,270 sin(90+30)) = 50,270
Зона выпадения зерен из ячейки определится разностью углов:
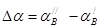 , , 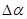 = 50,27-23,9 = 24,170 = 50,27-23,9 = 24,170
3. Определить форму и размеры приемного желоба
После нахождения значения верхней и нижней границ зон выпадения зерен из ячеек необходимо построить траектории свободного полета зерна, выпавшего из ячейки со скоростью V= R. Для этого надо рассчитать координаты X и Y для каждой траектории согласно уравнений: R. Для этого надо рассчитать координаты X и Y для каждой траектории согласно уравнений:
Реклама

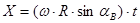 ; ;
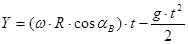 ; ;
При 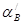
| t |
0,05 |
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
0,35 |
0,4 |
0,45 |
0,5 |
| X |
0,018 |
0,035 |
0,053 |
0,07 |
0,088 |
0,11 |
0,12 |
0,14 |
0,16 |
0,176 |
| Y |
0,028 |
-0,031 |
0,01 |
-0,035 |
-0,105 |
-0,12 |
-0,32 |
-0,46 |
-0,63 |
-0,82 |
При 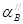
| t |
0,05 |
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
0,35 |
0,40 |
0,45 |
0,5 |
| X |
0,034 |
0,0676 |
0,101 |
0,135 |
0,169 |
0,202 |
0,236 |
0,27 |
0,3 |
0,338 |
| Y |
0,016 |
0,007 |
-0,026 |
-0,084 |
-0,166 |
-0,273 |
-0,4 |
-0,56 |
-0,7 |
-0,94 |
По расчетным значениям X и Y построить траектории свободного полета зерен из ячеек при 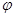 min
и min
и 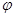 max
. max
.
Выбрать параметры желоба.
Желоб должен улавливать все выпадающие из ячеек зерна. Это возможно, если передняя стенка желоба установлена ниже наименьшего угла выпадения частиц из ячеек. При этом угол наклона стенки к горизонтали должен быть больше угла трения попавших в желоб зерен. Это условие будет соблюдено, если радиус закругления дна желоба будет удовлетворять условию:
r > R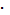 sin ( sin (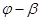 ); );
r > 0.2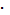 sin(450
- 200
); sin(450
- 200
);
примем r = 80 мм;
где : r- радиус закругления дна желоба, мм;
R- радиус триерного цилиндра, мм;
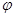 - угол трения, ( - угол трения, (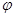 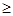 450
); 450
);
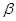 - центральный угол, определяющий положение кромки желоба - центральный угол, определяющий положение кромки желоба
(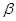 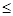 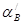 ), ),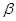 = 350
. = 350
.
Зазор между кромками стенок желоба и ячеистой поверхностью цилиндра принимаем a= 5 мм.
ВЫВОД: В результате построений и расчетов выяснили что, длинна триера L = 1,17 м; определили предельное положение зерна, находящееся в состоянии относительного покоя 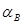 = 30,3 0
определили верхнюю и нижнюю границу зоны выпадения зерна из ячейки = 30,3 0
определили верхнюю и нижнюю границу зоны выпадения зерна из ячейки 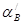 = 23,9 0
, = 23,9 0
, 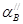 = 50,270
; зона выпадения зерен из ячейки = 50,270
; зона выпадения зерен из ячейки 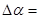 24,17 0
. 24,17 0
.
|