|
2. ЛИТЕРАТУРА
2.1 Основная литература
1. Опадчий Ю.Ф. и др. Аналоговая и цифровая электроника. – М.: Радио и связь, 2002. – 768 с.
2. Степаненко И.П. Основы микроэлектроники: Учеб. пособие для вузов. – М.: Лаборатория Базовых Знаний, 2000. – 488 с.
3. Ермаков А. Е. Схемотехника ЭВМ. Учебное пособие. -М.: РГОТУПС, 1997. – 352 с.
4.
Семененко В.А., Скуратович Э.К. Арифметико-логические основы компьютерной схемотехники. Учебное пособие для высшей школы (Серия "Gaudeamus"). – М.: Академ. проект, 2004. – 144 с.
5. Угрюмов Е.П. Цифровая схемотехника. BHV-Санкт-Петербург, 2004. – 528 с.
6.
Новиков Ю.В. Основы цифровой схемотехники: Базовые элементы и схемы. Методы проектирования. М., Мир. – 2001. – 379 с.
7. Разевиг В. Д. Система схемотехнического моделирования MICRO-CAP. – М.: Издательство «СОЛОН», 1997. – 373 с.
2.2 Дополнительная литература
1. Прянишников В.А. Электроника: Курс лекций. – СПб.: КОРОНА принт, 1998. – 400 с.
2. Гусев В.Г., Гусев М.Ю. Электроника. – М.: Высш.шк. 1991. – 495 с.
3. Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство – М.: Мир. 1982. – 512 с.
4. Гершунский Б.С. Основы электроники и микроэлектроники: Учебник для вузов – Киев: Высща школа, 1989. – 424 с.
5. Хоровиц П., Хилл У. Искусство схемотехники. В трех томах. - М. Мир, 1993.
Тема. Логические основы схемотехники
 Алгебра логики
— это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания. Алгебра логики
— это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Создателем алгебры логики является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний
.
Логическое высказывание
— это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.
Так, например, предложение “6 — четное число
” следует считать высказыванием, так как оно истинное. Предложение “Рим — столица Франции
” тоже высказывание, так как оно ложное.
Разумеется, не всякое предложение является логическим высказыванием
. Высказываниями не являются, например, предложения “ученик десятого класса
” и “информатика — интересный предмет
”. Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие “интересный предмет
”. Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.
Реклама

Предложения типа “в городе A
более миллиона жителей
”, “у него голубые глаза
” не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами
.
Высказывательная форма
— это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным. Заметим, что зачастую трудно установить истинность высказывания
. Так, например, высказывание “площадь поверхности Индийского
океана равна 75 млн кв. км
” в одной ситуации можно посчитать ложным, а в другой — истинным. Ложным — так как указанное значение неточное и вообще не является постоянным. Истинным — если рассматривать его как некоторое приближение, приемлемое на практике.
Употребляемые в обычной речи слова и словосочетания "не”, “и”, “или”, “если... , то”, “тогда и только тогда”
и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками
.
Bысказывания, образованные из других высказываний с помощью логических связок, называются составными
. Высказывания, не являющиеся составными, называются элементарными
.
Так, например, из элементарных высказываний “Петров — врач
”, “Петров — шахматист
” при помощи связки “и
” можно получить составное высказывание “Петров — врач и шахматист
”, понимаемое как “Петров — врач, хорошо играющий в шахматы
”.
При помощи связки “или
” из этих же высказываний можно получить составное высказывание “Петров — врач или шахматист
”, понимаемое в алгебре логики как “Петров или врач, или шахматист, или и врач и шахматист одновременно
”.
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
Чтобы обращаться к логическим высказываниям, им назначают имена.
Пусть через А
обозначено высказывание “Тимур поедет летом на море
”, а через В
— высказывание “Тимур летом отправится в горы
”. Тогда составное высказывание “Тимур летом побывает и на море, и в горах
” можно кратко записать как А и В
. Здесь “и
” — логическая связка, А
, В
— логические переменные, которые мoгут принимать только два значения — “истина
” или “ложь
”, обозначаемые, соответственно, “1” и “0”
Реклама

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:
(1)
Операция, выражаемая словом “не
”, называется отрицанием
и обозначается чертой над высказыванием. Высказывание 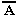 истинно, когда A ложно, и ложно, когда A истинно. Пример. “Луна — спутник Земли
” (А); “Луна — не спутник Земли
” ( истинно, когда A ложно, и ложно, когда A истинно. Пример. “Луна — спутник Земли
” (А); “Луна — не спутник Земли
” (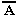 ). ).
(2)
Операция, выражаемая связкой “и
”, называется конъюнкцией
(лат. conjunctio — соединение) или логическим умножением и обозначается точкой "•" (может также обозначаться знаком &). Высказывание А•В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание
“10 делится на 2 и 5 больше 3”
истинно, а высказывания
“10 делится на 2 и 5 не больше 3”,
“10 не делится на 2 и 5 больше 3”,
“10 не делится на 2 и 5 не больше 3”
ложны.
(3)
Операция, выражаемая связкой “или
”
(в неразделительном, неисключающем смысле этого слова), называется дизъюнкцией
(лат. disjunctio — разделение) или логическим сложением
и обозначается знаком v
(или плюсом). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны
. Например, высказывание
“10 не делится на 2 или 5 не больше 3”
ложно, а высказывания
“10 делится на 2 или 5 больше 3”,
“10 делится на 2 или 5 не больше 3”,
“10 не делится на 2 или 5 больше 3”
истинны.
(4)
Операция, выражаемая связками “если ..., то
”, “из ... следует
”, “... влечет ...
”, называется импликацией
(лат. implico
— тесно связаны) и обозначается знаком ^. Высказывание А ^ В ложно тогда и только тогда, когда А истинно, а В — ложно.
Каким же образом импликация связывает два элементарных высказывания?
Покажем это на примере высказываний: “данный четырёхугольник — квадрат
” (А
) и “около данного четырёхугольника можно описать окружность
” (В
). Рассмотрим составное высказывание А ^ В
, понимаемое как “если данный четырёхугольник квадрат, то около него можно описать окружность
”. Есть три варианта, когда высказывание А
^
В истинно:
1. А
истинно и В
истинно, то есть данный четырёхугольник квадрат, и около него можно описать окружность;
2. А
ложно и В
истинно, то есть данный четырёхугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырёхугольника);
3. A
ложно и B
ложно, то есть данный четырёхугольник не является квадратом, и около него нельзя описать окружность.
Ложен только один вариант: А истинно и В ложно
, то есть данный четырёхугольник является квадратом, но около него нельзя описать окружность.
В обычной речи связка “если ..., то
” описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться “бессмысленностью” импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими:
“если президент США — демократ, то в Африке водятся жирафы”,
“если арбуз — ягода, то в бензоколонке есть бензин”.
(5)
Операция, выражаемая связками “тогда и только тогда
”, "необходимо и достаточно
”, “... равносильно
...”, называется эквиваленцией
или двойной импликацией
и обозначается знаком ~ . Высказывание А ~ В истинно тогда и только тогда, когда значения А и В совпадают.
Например, высказывания
“24 делится на 6 тогда и только тогда, когда 24 делится на 3”,
“23 делится на 6 тогда и только тогда, когда 23 делится на 3”
истинны, а высказывания
“24 делится на 6 тогда и только тогда, когда 24 делится на 5”,
“21 делится на 6 тогда и только тогда, когда 21 делится на 3”
ложны.
Высказывания А и В, образующие составное высказывание А ~ В, могут быть совершенно не связаны по содержанию,
например: “три больше двух
” (А
), “пингвины живут в Антарктиде
” (В
). Отрицаниями этих высказываний являются высказывания “три не больше двух
” (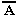 ), “пингвины не живут в Антарктиде
” ( ), “пингвины не живут в Антарктиде
” (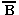 ). Образованные из высказываний А
, В
составные высказывания A~B
и ). Образованные из высказываний А
, В
составные высказывания A~B
и 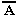 ~ ~
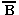 истинны, а высказывания A~ истинны, а высказывания A~
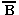 и и 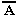 ~B
— ложны. ~B
— ложны.
Итак, нами рассмотрены пять логических операций: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
Импликацию
можно выразить через дизъюнкцию
и отрицание
:
А -> В = 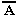 v В. v В.
Эквиваленцию
можно выразить через отрицание
, дизъюнкцию
и конъюнкцию
:
А <-> В = (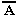 v В) • ( v В) • (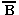 v А). v А).
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками.
Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (“не”), затем конъюнкция (“и”), после конъюнкции — дизъюнкция (“или”) и в последнюю очередь — импликация.
Логические формулы
С помощью логических переменных и символов логических операций любое высказывание можно формализовать,
то есть заменить логической формулой.
Определение логической формулы:
1.
Всякая логическая переменная и символы “истина” (“1”) и “ложь” (“0”) — формулы.
2.
Если А и В — формулы, то 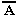 , (А • В), (А v В), (А ^ B), (А ~ В) — формулы. , (А • В), (А v В), (А ^ B), (А ~ В) — формулы.
3.
Никаких других формул в алгебре логики нет.
В п. 1 определены элементарные формулы
; в п. 2 даны правила образования из любых данных формул новых формул.
В качестве примера рассмотрим высказывание “если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог
”. Это высказывание формализуется в виде (A v B) ^ C
; такая же формула соответствует высказыванию “если Игорь знает английский или японский язык, то он получит место переводчика”.
Как показывает анализ формулы (A v B) ^ C
, при определённых сочетаниях значений переменных A
, B
и C
она принимает значение “истина”, а при некоторых других сочетаниях — значение “ложь” (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми
.
Некоторые формулы принимают значение “истина” при любых значениях истинности входящих в них переменных
. Таковой будет, например, формула Аv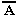 , соответствующая высказыванию “Этот треугольник прямоугольный или косоугольный
”. Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами
или тавтологиями
. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
, соответствующая высказыванию “Этот треугольник прямоугольный или косоугольный
”. Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами
или тавтологиями
. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
В качестве другого примера рассмотрим формулу А
•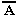 , которой соответствует, например, высказывание “Катя самая высокая девочка в классе, и в классе есть девочки выше Кати
”. Очевидно, что эта формула ложна, так как либо А
, либо , которой соответствует, например, высказывание “Катя самая высокая девочка в классе, и в классе есть девочки выше Кати
”. Очевидно, что эта формула ложна, так как либо А
, либо 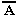 обязательно ложно. Такие формулы называются тождественно ложными формулами
или противоречиями
. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями. обязательно ложно. Такие формулы называются тождественно ложными формулами
или противоречиями
. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
Если две формулы А и В “одновременно”, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными
.
Равносильность двух формул алгебры логики обозначается символом “=”. Замена формулы другой, ей равносильной, называется равносильным преобразованием
данной формулы.
|