| Контрольная работа на тему:
«Матрицы, действия с ними»
1.
Историческая справка
Понятие Матрица (в математике) было введено в работах У. Гамильтона и А. Кэли в середине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом (2-я половина 19 века и начало 20 века). И.А. Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами. Матричные обозначения получили распространение в современной математике и её приложениях. Исчисление Матрица (в математике) развивается в направлении построения эффективных алгоритмов для численного решения основных задач.
2.
Раскрытие темы
Понятие о матрице
Матрица – множество чисел, образующих прямоугольную таблицу, которая содержит m-строк и n-столбцов. Для обозначения матрицы используется надпись:

aij
, I – номер строки, j – номер столбца.
Элементы матрицы, стоящие на диагонали, идущие из верхнего левого угла называют главной диагональю, другую диагональ называют побочной.
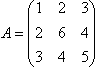 пример 1. пример 1.
Элементы главной диагонали: 1,6,5. Побочной диагонали: 3,6,3. (пример 1)
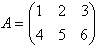 пример 2. пример 2.
Если количество строк m матрицы не равно количеству столбцов n, то матрица называется прямоугольной (пример 2).
Если количество столбцов матрицы совпадают с количеством строк, то матрица называется квадратной (пример 1).
Количество строк или столбцов в квадратной матрице называются ее порядком.
Если все элементы квадратной матрицы, кроме элементов главной диагонали, равны нулю, то матрица называется диагональной (пример 3).
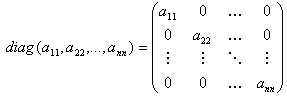 пример3 пример3
Если все числа главной диагонали равны единице, то матрица называется единичной (пример 4).
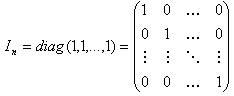 пример 4 пример 4
Если в прямоугольной матрице m*n m=1, то получается матрица-строка (пример 5).
xT
= (2 3 5). пример 5.
Если n=1, то получается матрица-столбец (пример 6).
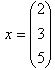 пример 6. пример 6.
Матрицы-строки матрицы-столбцы называются векторами.
Свойства матриц:
- A + (B + C) = (A + B) + C
- A + B = B + A
- A(BC) = (AB) C
- A (B + C) = AB + AC
- (B + C) A = BA + CA
- (AT) T = A
- (A * B) T = BT * AT
Действия с матрицами
1.
Сложение матриц
Матрицы одинакового размера можно складывать.
Суммой двух таких матриц А и В называется матрица С, элементы которой равны сумме соответствующих элементов матриц А и В. Символически будем записывать так: А+В=С.
Реклама

Пример.
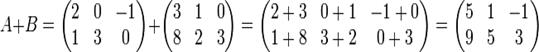
Легко видеть, что сложение матриц подчиняется переместительному и сочетательному законам:
А+В=В+А
(А+В)+С=А+(В+С).
Нулевая матрица при сложении матриц выполняет роль обычного нуля при сложении чисел: А+0=А.
2.
Вычитание матриц.
Разностью двух матриц А и В одинакового размера называется матрица С, такая, что
С+В=А
Из этого определения следует, что элементы матрицы С равны разности соответствующих элементов матриц А и В.
Обозначается разность матриц А и В так: С=А – В.
Пример.
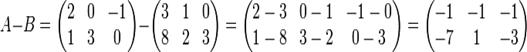
3. Умножение матриц
Рассмотрим правило умножения двух квадратных матриц второго порядка.
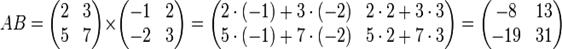
Произведением матрицы А на матрицу В называется матрица С=АВ.
Правила умножения прямоугольных матриц:
- Умножение матрицы А на матрицу В имеет смысл в том случае, когда число столбцов матрицы А совпадает с числом строк в матрице В.
- В результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк было в первой матрице и столько столбцов, сколько столбцов было во второй матрице.
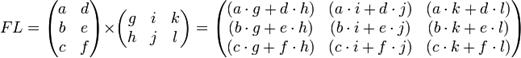
4. Умножение матрицы на число
При умножении матрицы A на число a
все числа, составляющие матрицу A, умножаются на число a
. Например, умножим матрицу 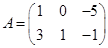 на число 2. Получим на число 2. Получим 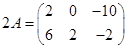 , т.е. при умножении матрицы на число множитель «вносится» под знак матрицы. , т.е. при умножении матрицы на число множитель «вносится» под знак матрицы.
5.
Транспонирование матрицы
Транспонированная матрица – матрица AТ
, полученная из исходной матрицы A заменой строк на столбцы.
Формально, транспонированная матрица для матрицы A размеров m*n – матрица AT
размеров n*m, определённая как AT
[i, j] = A [j, i].
Например,
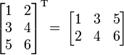
Свойства транспонированных матриц
1. (AT
)T
= A
2. (A + B)T
= AT
+ BT
3. (AB)T
= BT
AT
4. detA = detAT
Список литературы
1. Баврин, Матросов В.Л. Высшая математика: Учебник для студентов ВУЗов – М.: 2002.
2. Беллман Р. Введение в теорию матриц. – М.: Мир, 1969
3. Дж. Голуб, Ч. Ван Лоун Матричные вычисления. – М.: Мир, 1999.
|