|
ИССЛЕДОВАНИЕ ВЗАИМОСВЯЗЕЙ ПОКАЗАТЕЛЕЙ ФИНАНСОВЫХ РЫНКОВ:
|
| В таблице представлены среднемесячные данные за 2002 - 2004 гг:
|
| Годы
|
Месяцы
|
Курс $
|
Процентные ставки
|
Сальдо ТБ
|
Прирост ЗВР
|
ИПЦ
|
| |
|
Y
|
X1
|
X2
|
X3
|
Х4
|
| 2002
|
1
|
30,47272
|
10,1
|
3850
|
284
|
103,1
|
| 2
|
30,8057
|
10
|
3504
|
-214
|
101,2
|
| 3
|
31,06427
|
10,7
|
4722
|
452
|
101,1
|
| 4
|
31,17359
|
10,7
|
5390
|
435
|
101,2
|
| 5
|
31,25488
|
11,1
|
4814
|
1860
|
101,7
|
| 6
|
31,40493
|
11,1
|
4265
|
3072
|
100,5
|
| 7
|
31,51499
|
12
|
4883
|
1352
|
100,7
|
| 8
|
31,55431
|
10,3
|
5863
|
-285
|
100,1
|
| 9
|
31,62666
|
10,5
|
5603
|
1033
|
100,4
|
| 10
|
31,69333
|
12,4
|
5151
|
1292
|
101,1
|
| 11
|
31,81074
|
12,8
|
4644
|
1148
|
101,6
|
| 12
|
31,83684
|
12
|
5797
|
1438
|
101,5
|
| 2003
|
13
|
31,81617
|
12,1
|
5847
|
-412
|
102,4
|
| 14
|
31,69898
|
11,9
|
5636
|
1481
|
101,6
|
| 15
|
31,45329
|
11,2
|
6671
|
3787
|
101,1
|
| 16
|
31,21179
|
10,9
|
5137
|
2464
|
101
|
| 17
|
30,90706
|
10,8
|
5614
|
4322
|
100,8
|
| 18
|
30,46863
|
11
|
6261
|
5035
|
100,8
|
| 19
|
30,36029
|
11,1
|
6087
|
-452
|
100,7
|
| 20
|
30,34903
|
10,6
|
6948
|
24
|
99,6
|
| 21
|
30,59863
|
9,8
|
6378
|
-1702
|
100,3
|
| 22
|
30,16471
|
10,4
|
7010
|
-679
|
101
|
| 23
|
29,80797
|
10,4
|
6158
|
2855
|
101
|
| 24
|
29,4337
|
11
|
7192
|
3241
|
101,1
|
| 2004
|
25
|
28,8388
|
10
|
6894
|
8769
|
101,8
|
| 26
|
28,51467
|
9,4
|
6880
|
7052
|
101
|
| 27
|
28,52926
|
9,2
|
7412
|
2328
|
100,8
|
| 28
|
28,68563
|
9
|
8742
|
-2920
|
101
|
| 29
|
28,98922
|
9,2
|
7956
|
-734
|
100,7
|
| 30
|
29,02972
|
8,8
|
8762
|
2948
|
100,8
|
| 31
|
29,08193
|
9
|
8950
|
2614
|
100,9
|
| 32
|
29,21929
|
9,2
|
10253
|
384
|
100,4
|
| 33
|
29,22208
|
9,5
|
9767
|
92
|
100,4
|
| 34
|
29,0703
|
9,5
|
10223
|
6380
|
101,1
|
| 35
|
28,59119
|
9,6
|
10393
|
12256
|
101,1
|
| 36
|
27,90403
|
9,6
|
10467
|
10096
|
101,1
|
| Задание:
|
| 1.Проанализировать связи между данными пятью показателями по следующей схеме:
|
| а) оценить тесноту и напрвление связи для каждой пары величин
|
| б) выделить мультиколлениарные факторы
|
| в) выбрать два ведущих фактора для показателя "Курс доллара"
|
| 2. Построить линейную модель регрессии с ведущими факторами, пояснить экономический смысл
|
| ее параметров
|
| 3. Оценит качественные характеристики по следующей схеме:
|
| а) проверить статистическую значимость уравнения и его параметров
|
| б) проверить предпосылки МНК, определив математическое ожидание остатков и исследовав их на
|
| гомоскедастичность
|
| в) оценить уровень точности модели на основе средней относительной ошибки
|
| г) оценить какая доля вариации показателя "Курс доллара" учтена в построенной модели и
|
| обусловлена включенными в нее факторами
|
| 4.Выполнить прогноз показптеля "Курс доллара" на январь, февраль, март 2005г, определив ошибку
|
| прогнозирования с доверительной вероятностью 95%.
|
| Сравнить полученные результаты с фактическими данными за 2005:
Реклама

|
| январь - 28,009
|
| февраль - 27,995
|
| март - 27,626
|
| РЕШЕНИЕ:
|
| 1. Проанализируем связь между показателями:
|
| а) Оценим тесноту и напрвление связи для каждой пары величин.
|
| Тесноту и направление связи оценим по коэффициенту парной корреляции.
|
| Строим матрицу парных коэффициентов корреляции:
|
| |
Y
|
X1
|
X2
|
X3
|
Х4
|
| Y
|
1
|
| X1
|
0,829
|
1
|
| X2
|
-0,791
|
-0,656
|
1
|
| X3
|
-0,443
|
-0,163
|
0,389
|
1
|
| Х4
|
0,137
|
0,277
|
-0,292
|
0,120
|
1
|
| Проанализируем связь между зависимой переменной Y и факторами:
|
| r(Y;X1) =
|
0,829
|
- связь очень тесная и прямая, с увеличением фактора X1, зависимая
|
| |
переменная Y увеличивается.
|
| r(Y;X2) =
|
-0,791
|
- связь тесная и обратная, с увеличением фактора X2, зависимая переменная
|
| |
Y уменьшается.
|
| r(Y;X3) =
|
-0,443
|
- связь между зависимой переменной Y и фактором X3 слабая и обратная.
|
| r(Y;X4) =
|
0,137
|
- связи между результатом Y и фактором X4 практически нет.
|
ВЫВОД: Фактор x4 практически не оказывает влияния на зивисимую переменную Y, значит его следует исключить из модели.
| Проанализируем связь между факторами:
|
| r(X1;X2) =
|
-0,656
|
- связь между факторами X1 и X2 тесная и обратная.
|
| r(X1;X3) =
|
-0,163
|
- связь между факторами X1 и X3 практически отсутствует.
|
| r(X1;X4) =
|
0,277
|
- связь между факторами X1 и X4 очень слабая и прямая.
|
| r(X2;X3) =
|
0,389
|
- связь между факторами X2 и X3 слабая и прямая.
|
| r(X2;X4) =
|
-0,292
|
- связь между факторами X2 и X4 очень слабая и обратная.
|
| r(X3;X4) =
|
0,120
|
- связи между факторами X3 и X4 практически нет.
|
ВЫВОД: Факторы x1 и x2 приближены к линейно зависимым, поэтому вместе в модель их включать не следует.
Для проверки значимости коэффициентов применяем критерий Стьюдента:
| r
|
tr
|
Найдем расчетное значение t - критерия Стьюдента:
|
| 0,829
|
8,63
|
значим
|
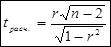
|
|
|
| -0,791
|
-7,55
|
значим
|
|
| -0,443
|
-2,88
|
значим
|
t (a=0,05;34) =
|
2,032
|
| 0,137
|
0,81
|
не значим
|
|
| -0,656
|
-5,07
|
значим
|
|
| -0,163
|
-0,96
|
не значим
|
Если tрасч. > tтабл.,то коэффициент парной
|
| 0,277
|
1,68
|
не значим
|
корреляции значим.
|
| 0,389
|
2,47
|
значим
|
| -0,292
|
-1,78
|
не значим
|
| 0,120
|
0,70
|
не значим
|
| в) Выбрать два ведущих фактора для показателя "Курс доллара"
|
| r(Y;X1) =
|
0,829
|
| r(Y;X2) =
|
-0,791
|
| Т.к. зависимая переменная Y теснее связана с фактором X1, значит фактор X2 из модели исключаем.
|
| Результаты исследования показали, что в модель следует включить факторы X1 и X3.
|
| Переобозначим фактор X3 как фактор X2, тогда уравнение регрессии имеет вид:
|
| Y (x1,x2) = a0 + a1*x1 + a2*x2 - уравнение множественной регрессии.
|
2. Строим линейную модель регрессии:
| Y
|
X1
|
X2
|
Yрасч.
|
Ex
|
E^2
|
(E-Eср)^2
|
(Et - Et-1)^2
|
E/Y
|
(Y-Yср)^2
|
| 30,472715
|
10,1
|
284
|
30,14
|
0,33
|
0,11
|
0,104
|
-
|
0,011
|
0,02983
|
| 30,8057
|
10
|
-214
Реклама

|
30,10
|
0,70
|
0,50
|
0,482
|
0,139
|
0,023
|
0,255732
|
| 31,0642667
|
10,7
|
452
|
30,66
|
0,41
|
0,17
|
0,157
|
0,089
|
0,013
|
0,584104
|
| 31,1735864
|
10,7
|
435
|
30,66
|
0,51
|
0,26
|
0,254
|
0,012
|
0,016
|
0,763153
|
| 31,2548842
|
11,1
|
1860
|
30,87
|
0,38
|
0,15
|
0,138
|
0,017
|
0,012
|
0,911804
|
| 31,40493
|
11,1
|
3072
|
30,75
|
0,65
|
0,43
|
0,414
|
0,074
|
0,021
|
1,22087
|
| 31,5149864
|
12
|
1352
|
31,72
|
-0,21
|
0,04
|
0,048
|
0,745
|
0,007
|
1,476192
|
| 31,5543087
|
10,3
|
-285
|
30,38
|
1,18
|
1,39
|
1,366
|
1,928
|
0,037
|
1,57329
|
| 31,626655
|
10,5
|
1033
|
30,42
|
1,20
|
1,45
|
1,428
|
0,001
|
0,038
|
1,760013
|
| 31,6933261
|
12,4
|
1292
|
32,09
|
-0,39
|
0,15
|
0,163
|
2,555
|
0,012
|
1,941358
|
| 31,8107429
|
12,8
|
1148
|
32,46
|
-0,65
|
0,42
|
0,431
|
0,064
|
0,020
|
2,282344
|
| 31,83684
|
12
|
1438
|
31,72
|
0,12
|
0,01
|
0,012
|
0,588
|
0,004
|
2,361877
|
| 31,816165
|
12,1
|
-412
|
31,99
|
-0,17
|
0,03
|
0,034
|
0,087
|
0,005
|
2,298756
|
| 31,6989789
|
11,9
|
1481
|
31,62
|
0,08
|
0,01
|
0,004
|
0,063
|
0,002
|
1,957142
|
| 31,45329
|
11,2
|
3787
|
30,77
|
0,68
|
0,47
|
0,454
|
0,370
|
0,022
|
1,330078
|
| 31,2117864
|
10,9
|
2464
|
30,63
|
0,58
|
0,33
|
0,322
|
0,011
|
0,018
|
0,831354
|
| 30,907055
|
10,8
|
4322
|
30,36
|
0,55
|
0,30
|
0,289
|
0,001
|
0,018
|
0,368516
|
| 30,4686263
|
11
|
5035
|
30,47
|
0,00
|
0,00
|
0,000
|
0,297
|
0,000
|
0,028435
|
| 30,360287
|
11,1
|
-452
|
31,10
|
-0,74
|
0,55
|
0,568
|
0,557
|
0,025
|
0,003635
|
| 30,3490273
|
10,6
|
24
|
30,61
|
-0,26
|
0,07
|
0,074
|
0,232
|
0,009
|
0,002404
|
| 30,5986333
|
9,8
|
-1702
|
30,07
|
0,53
|
0,28
|
0,267
|
0,623
|
0,017
|
0,089182
|
| 30,164713
|
10,4
|
-679
|
30,50
|
-0,34
|
0,12
|
0,122
|
0,749
|
0,011
|
0,018303
|
| 29,807965
|
10,4
|
2855
|
30,15
|
-0,34
|
0,12
|
0,124
|
0,000
|
0,011
|
0,242098
|
| 29,4337
|
11
|
3241
|
30,65
|
-1,21
|
1,47
|
1,494
|
0,756
|
0,041
|
0,750476
|
| 28,838795
|
10
|
8769
|
29,20
|
-0,36
|
0,13
|
0,140
|
0,719
|
0,013
|
2,13512
|
| 28,5146737
|
9,4
|
7052
|
28,84
|
-0,33
|
0,11
|
0,113
|
0,001
|
0,011
|
3,18739
|
| 28,5292619
|
9,2
|
2328
|
29,14
|
-0,61
|
0,37
|
0,379
|
0,078
|
0,021
|
3,135513
|
| 28,6856318
|
9
|
-2920
|
29,48
|
-0,80
|
0,63
|
0,650
|
0,036
|
0,028
|
2,606185
|
| 28,9892167
|
9,2
|
-734
|
29,44
|
-0,45
|
0,20
|
0,214
|
0,118
|
0,016
|
1,718153
|
| 29,0297238
|
8,8
|
2948
|
28,72
|
0,31
|
0,10
|
0,092
|
0,585
|
0,011
|
1,613602
|
| 29,0819261
|
9
|
2614
|
28,93
|
0,15
|
0,02
|
0,021
|
0,025
|
0,005
|
1,483704
|
| 29,2192857
|
9,2
|
384
|
29,33
|
-0,11
|
0,01
|
0,014
|
0,070
|
0,004
|
1,167943
|
| 29,2220818
|
9,5
|
92
|
29,63
|
-0,40
|
0,16
|
0,171
|
0,086
|
0,014
|
1,161908
|
| 29,0703
|
9,5
|
6380
|
29,00
|
0,07
|
0,01
|
0,004
|
0,228
|
0,003
|
1,512162
|
| 28,591185
|
9,6
|
12256
|
28,50
|
0,09
|
0,01
|
0,007
|
0,000
|
0,003
|
2,920049
|
| 27,9040273
|
9,6
|
10096
|
28,71
|
-0,81
|
0,66
|
0,673
|
0,816
|
0,029
|
5,740685
|
| 1090,15928
|
376,9
|
81096
|
1089,81
|
0,35
|
11,23
|
11,227
|
12,72
|
0,552
|
51,46
|
| 30,3
|
|
|
|
0,01
|
|
|
|
| ВЫВОД ИТОГОВ
|
| Регрессионная статистика
|
|
| Множественный R
|
0,885
|
| R-квадрат
|
0,784
|
| Нормированный R-квадрат
|
0,771
|
| Стандартная ошибка
|
0,580
|
| Наблюдения
|
36
|
| Дисперсионный анализ
|
| |
df
|
SS
|
MS
|
F
|
| Регрессия
|
2
|
40,33
|
20,17
|
59,86
|
| Остаток
|
33
|
11,12
|
0,34
|
| Итого
|
35
|
51,45
|
| |
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
Нижние 95%
|
Верхние 95%
|
| Y-п. (а0)
|
21,1762
|
1,0069
|
21,0320
|
19,1277
|
23,2247
|
| X1 (а1)
|
0,8949
|
0,0944
|
9,4749
|
0,7027
|
1,0870
|
| X2 (а2)
|
-0,0001
|
0,0000
|
-3,8556
|
-0,0002
|
-0,0001
|
| Yрасч. = 21,18 + 0,89*x1 - 0,0001*x2
- двуфактрная линейная модель регрессии.
|
| а1 = 0,89 - если процентные ставки увеличить на единицу измерения, то курс доллара увеличится на 0,89 единиц.
|
| а2 = -0,0001 - если прирост ЗВР увеличить на единицу измерения, то курс доллара снизится на 0,0001 единиц.
|
3. Оценим качественные характеристики по следующей схеме:
а) Проверим статистическую значимость уравнения и его параметров:
| Для проверки значимости уравнения регрессии рассчитаем критерий Фишера.
|
| 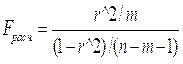
|
|
|
|
|
| =
|
59,86
|
>
|
F (0,05;2;33) =
|
3,285
|
a=0,05
|
| n1 = k = 2
|
| n2 =n-k-1=36-2-1 =33
|
| Fрасч. > Fтабл. -
|
значит уравнение регрессии статистически значимо, т.е. адекватно.
|
| Проверка значимости параметров уравнения осуществляется по крит. Стьюдента:
|
| Расчетные значения критерия Стьюдента для всех параметров возьмем из таллицы:
|
| t (a0) =
|
21,03
|
>
|
2,03
|
| t (a1) =
|
9,47
|
>
|
2,03
|
t (a ; n-m-1) = t (0,05;33) =
|
2,03
|
| t (a2) =
|
-3,86
|
>
|
2,03
|
| ВЫВОД: Все коэффициенты регрессии статистически значимы, т.е. значимо отличаются от нуля
|
| с ошибкой в 5%.
|
| Интервальные оценки параметров:
|
| а0 = (19,13 : 23,22) - параметр значим.
|
| а1 = (0,7 : 1,09) - параметр значим.
|
| а2 = (-0,0002 : -0,0001) - параметр значим.
|
б) Проверим выполнение предпосылок МНК:
| 1) Равенство нулю математического ожидания:
|
|
| 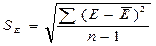
|
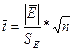
|
| =
|
0,57
|
=
|
0,1
|
<
|
t (0,05;35) =
|
2,03
|
| ВЫВОД: Математическое ожидание стремитсям к нулю, свойство выполнено.
|
| 2) Случайность значений остатков (критерий поворотных точек или крит. пиков):
|
| |
|
|
|
| m = 19 -
|
число поворотных точек
|
|
|
| '=' [
|
17,7
|
] =
|
17
|
m > 17 условие выполняется, значит колебания остаточной компоненты являются случайными.
ВЫВОД: Свойство выполнено.
График остатков
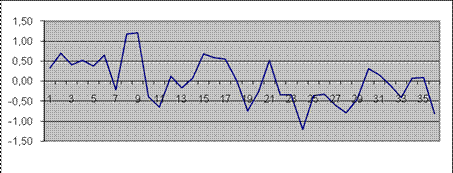
3) Отсутствие автокорреляции в ряду остатков или независимость значений остатков (критерий Дарбина-Уотсона):
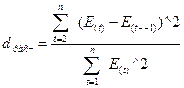
| =
|
1,13
|
Критические границы:
|
d1 = 1,29
|
| d2 = 1,45
|
| d расч. < d1 - остатки содержат автокорреляцию.
|
| ВЫВОД: Свойство не выполнено.
|
4) Нормальный закон распределения остатков (R/S критерий):
Расчитаем среднеквадратическое отклонение:
| =
|
0,57
|
Критические границы:
|
| (3,58 : 5,04)
|
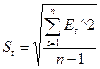
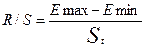
= 4,27
| 3,58 < 4,27 < 5,04 - расчитанное значение R/S-критерия попадает в границы.
|
| ВЫВОД: Свойство выполнено, остатки подчиняются нормальному закону распределения.
|
| 5) Гомоскедостичность остатков:
|
| Ранжируем ряд в порядке возрастания фактора X1:
|
| Y
|
X1
|
X2
|
Y
|
X1
|
X2
|
| 30,472715
|
10,1
|
284
|
29,0297238
|
8,8
|
2948
|
| 30,8057
|
10
|
-214
|
28,6856318
|
9
|
-2920
|
| 31,0642667
|
10,7
|
452
|
29,0819261
|
9
|
2614
|
| 31,1735864
|
10,7
|
435
|
28,5292619
|
9,2
|
2328
|
| 31,2548842
|
11,1
|
1860
|
28,9892167
|
9,2
|
-734
|
| 31,40493
|
11,1
|
3072
|
29,2192857
|
9,2
|
384
|
| 31,5149864
|
12
|
1352
|
28,5146737
|
9,4
|
7052
|
| 31,5543087
|
10,3
|
-285
|
29,2220818
|
9,5
|
92
|
| 31,626655
|
10,5
|
1033
|
29,0703
|
9,5
|
6380
|
| 31,6933261
|
12,4
|
1292
|
28,591185
|
9,6
|
12256
|
| 31,8107429
|
12,8
|
1148
|
27,9040273
|
9,6
|
10096
|
| 31,83684
|
12
|
1438
|
30,5986333
|
9,8
|
-1702
|
| 31,816165
|
12,1
|
-412
|
30,8057
|
10
|
-214
|
| 31,6989789
|
11,9
|
1481
|
28,838795
|
10
|
8769
|
| 31,45329
|
11,2
|
3787
|
30,472715
|
10,1
|
284
|
| 31,2117864
|
10,9
|
2464
|
31,5543087
|
10,3
|
-285
|
| 30,907055
|
10,8
|
4322
|
30,164713
|
10,4
|
-679
|
| 30,4686263
|
11
|
5035
|

|
29,807965
|
10,4
|
2855
|
| 30,360287
|
11,1
|
-452
|
31,626655
|
10,5
|
1033
|
| 30,3490273
|
10,6
|
24
|
30,3490273
|
10,6
|
24
|
| 30,5986333
|
9,8
|
-1702
|
31,0642667
|
10,7
|
452
|
| 30,164713
|
10,4
|
-679
|
31,1735864
|
10,7
|
435
|
| 29,807965
|
10,4
|
2855
|
30,907055
|
10,8
|
4322
|
| 29,4337
|
11
|
3241
|
31,2117864
|
10,9
|
2464
|
| 28,838795
|
10
|
8769
|
30,4686263
|
11
|
5035
|
| 28,5146737
|
9,4
|
7052
|
29,4337
|
11
|
3241
|
| 28,5292619
|
9,2
|
2328
|
31,2548842
|
11,1
|
1860
|
| 28,6856318
|
9
|
-2920
|
31,40493
|
11,1
|
3072
|
| 28,9892167
|
9,2
|
-734
|
30,360287
|
11,1
|
-452
|
| 29,0297238
|
8,8
|
2948
|
31,45329
|
11,2
|
3787
|
| 29,0819261
|
9
|
2614
|
31,6989789
|
11,9
|
1481
|
| 29,2192857
|
9,2
|
384
|
31,5149864
|
12
|
1352
|
| 29,2220818
|
9,5
|
92
|
31,83684
|
12
|
1438
|
| 29,0703
|
9,5
|
6380
|
31,816165
|
12,1
|
-412
|
| 28,591185
|
9,6
|
12256
|
31,6933261
|
12,4
|
1292
|
| 27,9040273
|
9,6
|
10096
|
31,8107429
|
12,8
|
1148
|
Ранжированный ряд делим на две группы и находим для каждой уравнение регрессии:
Первая группа
| Y
|
X1
|
X2
|
| 29,0297238
|
8,8
|
2948
|
| 28,6856318
|
9
|
-2920
|
| 29,0819261
|
9
|
2614
|
| 28,5292619
|
9,2
|
2328
|
| 28,9892167
|
9,2
|
-734
|
| 29,2192857
|
9,2
|
384
|
| 28,5146737
|
9,4
|
7052
|
| 29,2220818
|
9,5
|
92
|
| 29,0703
|
9,5
|
6380
|
| 28,591185
|
9,6
|
12256
|
| 27,9040273
|
9,6
|
10096
|
| 30,5986333
|
9,8
|
-1702
|
| 30,8057
|
10
|
-214
|
| 28,838795
|
10
|
8769
|
| 30,472715
|
10,1
|
284
|
| 31,5543087
|
10,3
|
-285
|
| 30,164713
|
10,4
|
-679
|
| 29,807965
|
10,4
|
2855
|
ВЫВОД ИТОГОВ
| Регрессионная статистика
|
|
| Множественный R
|
0,858
|
| R-квадрат
|
0,735
|
| Нормированный R-квадрат
|
0,700
|
| Стандартная ошибка
|
0,528
|
| Наблюдения
|
18
|
| Дисперсионный анализ
|
| |
df
|
SS
|
MS
|
F
|
| Регрессия
|
2
|
11,62
|
5,81
|
20,85
|
| Остаток
|
15
|
4,18
|
0,28
|
| Итого
|
17
|
15,79
|
| |
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
Нижние 95,0%
|
Верхние 95,0%
|
| Y-пересечение
|
18,0795
|
2,4594
|
7,3511
|
12,8374
|
23,3216
|
| X1
|
1,2129
|
0,2552
|
4,7520
|
0,6689
|
1,7570
|
| X2
|
-0,0001
|
0,0000
|
-4,2681
|
-0,0002
|
-0,0001
|
| Получаем первое уравнение регрессии: Yрасч.(X) = 18,08 + 1,21*x1 - 0,0001*x2
|
| Определим для него остаточную сумму квадратов отклонений:
|
Вторая группа
| Y
|
X1
|
X2
|
| 31,626655
|
10,5
|
1033
|
| 30,3490273
|
10,6
|
24
|
| 31,0642667
|
10,7
|
452
|
| 31,1735864
|
10,7
|
435
|
| 30,907055
|
10,8
|
4322
|
| 31,2117864
|
10,9
|
2464
|
| 30,4686263
|
11
|
5035
|
| 29,4337
|
11
|
3241
|
| 31,2548842
|
11,1
|
1860
|
| 31,40493
|
11,1
|
3072
|
| 30,360287
|
11,1
|
-452
|
| 31,45329
|
11,2
|
3787
|
| 31,6989789
|
11,9
|
1481
|
| 31,5149864
|
12
|
1352
|
| 31,83684
|
12
|
1438
|
| 31,816165
|
12,1
|
-412
|
| 31,6933261
|
12,4
|
1292
|
| 31,8107429
|
12,8
|
1148
|
| ВЫВОД ИТОГОВ
|
| Регрессионная статистика
|
|
| Множественный R
|
0,577
|
| R-квадрат
|
0,333
|
| Нормированный R-квадрат
|
0,244
|
| Стандартная ошибка
|
0,567
|
| Наблюдения
|
18
|
| Дисперсионный анализ
|
| |
df
|
SS
|
MS
|
F
|
| Регрессия
|
2
|
2,399
|
1,200
|
3,737
|
| Остаток
|
15
|
4,816
|
0,321
|
| Итого
|
17
|
7,215
|
| |
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
Нижние 95,0%
|
Верхние 95,0%
|
| Y-пересечение
|
25,4945
|
2,3486
|
10,8554
|
20,4887
|
30,5004
|
| X1
|
0,5096
|
0,2040
|
2,4976
|
0,0747
|
0,9444
|
| X2
|
-0,0001
|
0,0001
|
-0,6220
|
-0,0002
|
0,0001
|
| Получаем второе уравнение регрессии: Yрасч.(X) = 25,5 + 0,51*x1 - 0,0001*x2
|
| Определим для него остаточную сумму квадратов отклонений:
|
Вычислим расчетный критерий Фишера:
| F расч. =
|
1,152
|
<
|
F (0,05;16;16) =
|
2,333
|
ВЫВОД: Т.к. расчетный критерий Фишера меньше табличного, значит гетероскидостичность отсутствует, остатки имеют постоянную дисперсию.
Свойство выполнено.
ВЫВОД:
Т.к. рядом остатков выполняются почти все свойства, модель можно считать вполне адекватной.
в) Оценим точность модели:
Расчитаем среднеквадратическое отклонение:
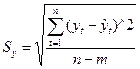
| =
|
0,580
|
(из регрессионной статистики)
|
| Расчитаем среднюю относительную ошибку апроксимации:
|
| 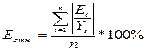
|
| =
|
1,53
|
%
|
<
|
7%
|
| ВЫВОД: Модель точная.
|
| г) Расчитаем коэффициент детерминации:
|
| 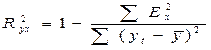
|
| =
|
0,782
|
= 78,2%
|
| ВЫВОД: 78,2% изменения курса доллара происходит под влиянием факторов, включенных в модель.
|
| 4. Прогнозирование на 3 месяца вперед:
|
| Yпрогн. = 21,18 + 0,89*x1(прогн.) - 0,0001*x2(прогн.)
|
| k
|
x1(прогн)
|
k
|
x2(прогн)
|
| 1
|
9,59
|
1
|
10376,3
|
| =
|
-0,01
|
2
|
9,57
|
2
|
10656,7
|
| =
|
280,3
|
3
|
9,56
|
3
|
10937,0
|
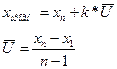
| Расчитаем прогнозное значение результата Y:
|
| Yпрогн.(37) = 21,18 + 0,89*9,59 - 0,0001*10376,3 = 28,54
|
| Yпрогн.(38) = 21,18 + 0,89*9,57 - 0,0001*10656,7 = 28,50
|
| Yпрогн.(39) = 21,18 + 0,89*9,59 - 0,0001*10376,3 = 28,45
|
В результате получим курс доллара на 3 месяца:
| Месяц
|
Данные
|
| расчетн.
|
фактич.
|
| январь
|
28,54
|
28,01
|
| февраль
|
28,50
|
28,00
|
| март
|
28,45
|
27,63
|
ВЫВОД: Как видно из таблицы прогнозные значения курса доллара, расчитанные по формуле, превышают значения фактических данных, но тенденция курса доллара к снижению сохраняется.
|