|
Заказ №1459
№1
Округлить сомнительные цифры числа а
, оставив верные цифры: а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата.
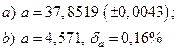
Решение
а) По условию 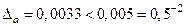 . Следовательно, в числе . Следовательно, в числе 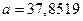 верными в узком смысле являются четыре цифры: 3, 7, 8, 5. Округляем число a
до четырех верными в узком смысле являются четыре цифры: 3, 7, 8, 5. Округляем число a
до четырех
значащих цифр: 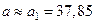 . Тогда . Тогда
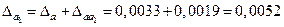
Так как 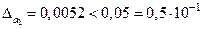 , то число a
1
имеет три верные цифры: 3, 7, 8. Округляем число a
до трех значащих цифр: , то число a
1
имеет три верные цифры: 3, 7, 8. Округляем число a
до трех значащих цифр: 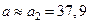 . Тогда . Тогда
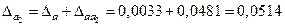
Так как 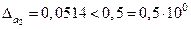 , то число a
2
имеет две верные цифры: 3, 7. Округляем число a
до двух значащих цифр: , то число a
2
имеет две верные цифры: 3, 7. Округляем число a
до двух значащих цифр: 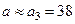 . Тогда . Тогда
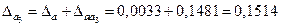
Так как 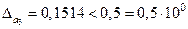 , то две оставшиеся цифры результата , то две оставшиеся цифры результата 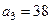 верны в узком смысле. Таким образом, верны в узком смысле. Таким образом,
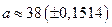
б) Представим 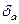 в виде в виде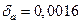 и найдем и найдем
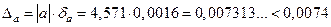
примем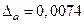 . Так как . Так как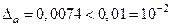 , то число a
= 4,571 имеет три верные в широком смысле цифры: 4, 5, 7. Округляем число a
до трех значащих цифр: , то число a
= 4,571 имеет три верные в широком смысле цифры: 4, 5, 7. Округляем число a
до трех значащих цифр: 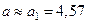 . Тогда . Тогда
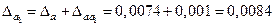
Так как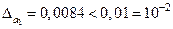 , то три оставшиеся цифры результата , то три оставшиеся цифры результата 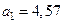 верны в широком смысле. Таким образом, верны в широком смысле. Таким образом,
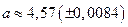 . .
Ответ:
а) 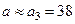 , , 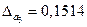 ; ;
б) 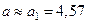 , , 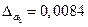
№2
Найти интерполяционный многочлен Лагранжа для данной функции f
(x
) с заданными узлами xk
(k
= 0, 1, 2, 3)
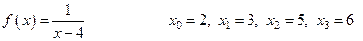
Решение
Прежде всего, заметим, что
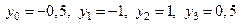
Применяя формулу (3) при n
= 3, получим:
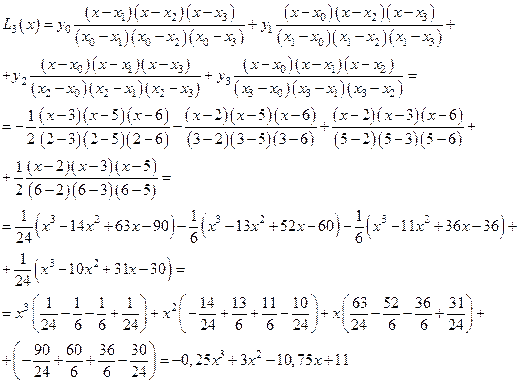
Ответ:
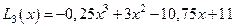
№3
Методом наименьших квадратов найти эмпирическую формулу вида y
= ax
+ b
по данным опыта, представленным таблицей
| х
|
1
|
2
|
3
|
4
|
5
|
| у
|
1,8
|
1,3
|
3,3
|
4,8
|
3,8
|
Решение
Результаты предварительных вычислений вносим в таблицу
| 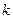
|
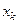
|
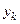
|
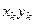
|
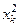
|
| 0
1
2
3
4
|
1
2
3
4
5
|
1,8
1,3
3,3
4,8
3,8
|
1,8
2,6
9,9
19,2
19
|
1
4
9
16
25
|
| 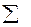
|
15
|
15
|
52,5
|
55
|
Нормальная система уравнений принимает вид
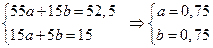
Следовательно, искомая эмпирическая формула
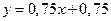
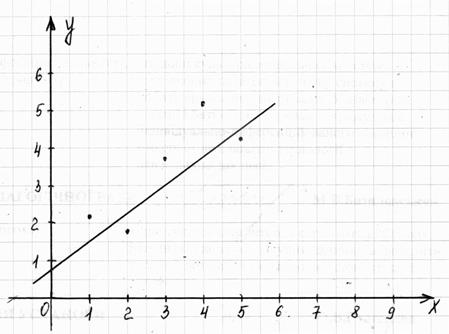
Ответ:
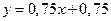
№4
Вычислить данный интеграл с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Вычисления производить с округлением до четвертого десятичного знака.
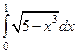
Решение
Определяем значения подынтегральной функции при 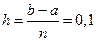 для следующих значений аргумента для следующих значений аргумента
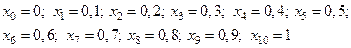
Находим соответствующие значения функции 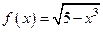 : :
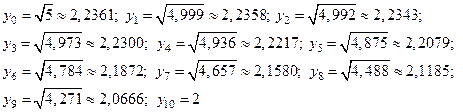
Тогда получаем
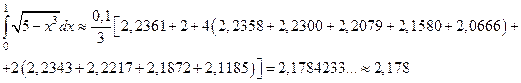
Ответ:
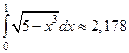
№5
Отделить корни данного уравнения аналитически и уточнить больший из них методом Ньютона с точностью до 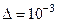
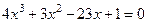
Решение
Отделим корни данного уравнения аналитически. Находим
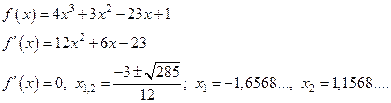
Составляем таблицу знаков функции
Уравнение имеет три действительных корня:
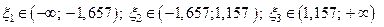
Уменьшим отрезки, содержащие корни, до длины, равной 1
| 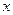
|
-3
|
-2
|
0
|
1
|
2
|
3
|
| 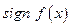
|
-
|
+
|
+
|
-
|
-
|
+
|
Значит, 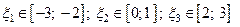
Уточним больший корень 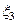 заданного уравнения методом Ньютона. Имеем заданного уравнения методом Ньютона. Имеем
Реклама

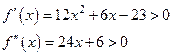
при 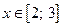 . Поэтому для использования метода Ньютона выбираем . Поэтому для использования метода Ньютона выбираем 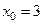 , причем , причем
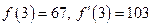 . Все вычисления сводим в таблицу . Все вычисления сводим в таблицу
| 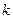
|
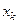
|
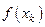
|
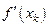
|
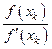
|
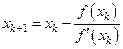
|
| 0
1
2
3
4
|
3
2,3495
2,0809
2,0285
2,0265
|
67
15,4003
2,1721
0,0765
-0,0005
|
103
57,3388
41,4471
38,5488
38,4394
|
0,651
0,267
0,0524
0,0020
0
|
2,3495
2,0809
2,0285
2,0265
2,0265
|
Искомый корень 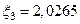
Ответ:
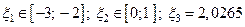
№6
Используя метод Эйлера, составить таблицу приближенных значений решения данного дифференциального уравнения y
’ = f
(x
, y
), удовлетворяющего начальному условию y
(1) = 0, на отрезке [1; 1,05] с шагом h
= 0,01. Вычисления вести с четырьмя знаками после запятой
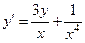
Решение
Находим последовательные значения аргумента
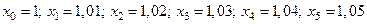
Обозначим
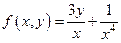
Для удобства вычислений составим таблицу
| 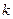
|
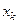
|
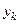
|
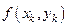
|
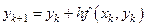
|
| 0
1
2
3
4
5
|
1
1,01
1,02
1,03
1,04
1,05
|
0
0,01
0,0199
0,0297
0,0395
0,0491
|
1
0,9907
0,9824
0,9750
0,9686
|
0,01
0,0199
0,0297
0,0395
0,0491
|
Таким образом, имеем следующую таблицу
| х
|
1
|
1,01
|
1,02
|
1,03
|
1,04
|
1,05
|
| у
|
0
|
0,01
|
0,0199
|
0,0297
|
0,0395
|
0,0491
|
Ответ:
таблица.
|