Глава 1. Собственные интегралы, зависящие от параметра
Пункт 1. Понятие интеграла, зависящего от параметра
Для того чтобы дать определение интеграла, зависящего от параметра, введем функцию  . Пусть эта функция . Пусть эта функция  будет определена на некотором множестве будет определена на некотором множестве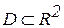 , где , где 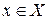 и и 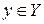 , то есть в результате получится множество , то есть в результате получится множество 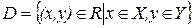 . Если функция . Если функция  непрерывна в D
, то тогда имеет смысл интеграл непрерывна в D
, то тогда имеет смысл интеграл 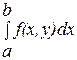 , где x
принадлежит некоторому конечному или бесконечному промежутку , где x
принадлежит некоторому конечному или бесконечному промежутку 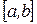 , значит, интеграл может быть несобственным. , значит, интеграл может быть несобственным.
На основании этого можно дать определение интеграла, зависящего от параметра.
Определение.
Интеграл 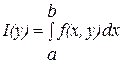 называется интегралом, зависящим от параметра, если называется интегралом, зависящим от параметра, если  интегрируема на промежутке интегрируема на промежутке 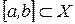 при любом фиксированным при любом фиксированным 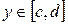 , где , где 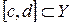 . .
Следовательно, 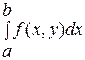 представляет собой функцию представляет собой функцию 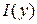 переменной (параметра) переменной (параметра) 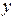 , определенную в промежутке , определенную в промежутке  . Возможно также существование интеграла при фиксированном . Возможно также существование интеграла при фиксированном 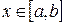 , тогда он будет представлять собой функцию переменной (параметра) , тогда он будет представлять собой функцию переменной (параметра) 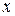 , определенную в промежутке , определенную в промежутке 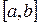 . Обозначается она так . Обозначается она так 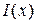 , так что , так что 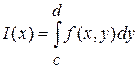 . .
Основная задача будет состоять в том, чтобы, зная свойства функции  , получить информацию о свойствах функции , получить информацию о свойствах функции 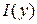 . Эти свойства имеют многообразные применения, особенно при вычислении несобственных интегралов. . Эти свойства имеют многообразные применения, особенно при вычислении несобственных интегралов.
Пример.
Найти интеграл 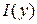 от функции от функции 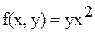 , , 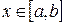
Функция 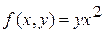 непрерывна на отрезке непрерывна на отрезке 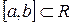 при любом фиксированном при любом фиксированном  , а значит, она интегрируема. Тогда , а значит, она интегрируема. Тогда
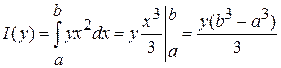 . .
Пункт 2. Предельный переход под знаком интеграла. Непрерывность интеграла как функции параметра
Определение.
Пусть 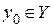 - это предельная точка множества - это предельная точка множества 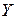 .Функция .Функция  называется равномерно сходящейся к функции называется равномерно сходящейся к функции 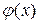 при при  по переменной по переменной 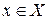 , если выполняются следующие условия: , если выполняются следующие условия:
1. для  при при  существует конечная предельная функция существует конечная предельная функция 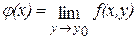 ; ;
2. 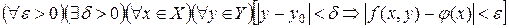 . (1) . (1)
Замечание 1.
В цепочки (1) 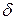 зависит только от зависит только от 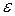 и не зависит от и не зависит от 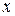 , а неравенство , а неравенство 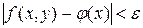 выполняется при любых выполняется при любых 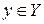 одновременно. одновременно.
Замечание 2.
Если 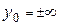 , то в цепочке (1) неравенство , то в цепочке (1) неравенство 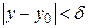 следует заменить на следует заменить на 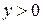 ( (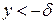 ). ).
Теорема 1 (признак сходимости).
Если функция  определена на множестве определена на множестве 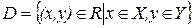 , то для того, чтобы она имела предельную функцию и сходилась к ней равномерно необходимо и достаточно, чтобы выполнялась цепочка , то для того, чтобы она имела предельную функцию и сходилась к ней равномерно необходимо и достаточно, чтобы выполнялась цепочка
 Докажем теорема так. Докажем теорема так.
Необходимость
. Пусть функция  равномерно сходится. Если заменим в определении равномерно сходится. Если заменим в определении 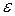 на на 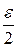 и выберем соответственно и выберем соответственно 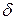 , а затем возьмем два значения , а затем возьмем два значения  и и 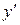 из из 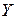 так, чтобы выполнялись условия так, чтобы выполнялись условия 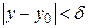 и и 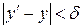 . В результате получим . В результате получим 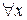 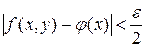 и и 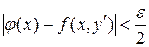 откуда следует последнее неравенство в цепочке откуда следует последнее неравенство в цепочке 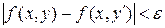 . .
Достаточность
. Теперь пусть существует предельная функция 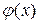 . Нужно доказать равномерную сходимость функции . Нужно доказать равномерную сходимость функции  к предельной функции. Для этого совершим переход к пределу в неравенстве к предельной функции. Для этого совершим переход к пределу в неравенстве 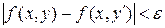 при при 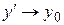 , получается , получается 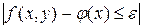 . Что и подтверждает равномерную сходимость . Что и подтверждает равномерную сходимость  к функции к функции 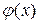 . .
Теорема 2 (о непрерывности предельной функции).
Если функция  при любом фиксированном при любом фиксированном 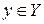 непрерывна на непрерывна на 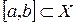 и равномерно сходится к предельной функции и равномерно сходится к предельной функции 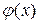 по переменной по переменной 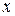 при при  , то функция , то функция 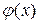 также непрерывна на также непрерывна на 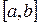 . .
Реклама

Легко обобщается теорема Дини: если функция  непрерывна для любого фиксированного непрерывна для любого фиксированного  на на 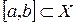 и при возрастании и при возрастании  функция, монотонно возрастая, стремится к предельной функции функция, монотонно возрастая, стремится к предельной функции 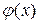 , то , то  сходится к сходится к 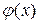 равномерно. равномерно.
Теорема 3 (предельный переход по параметру под знаком интеграла).
Если функция  непрерывна при постоянном значении непрерывна при постоянном значении  на на 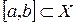 и сходится равномерно по переменной и сходится равномерно по переменной 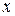 к предельной функции к предельной функции 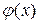 при при  , то тогда имеет место равенство , то тогда имеет место равенство
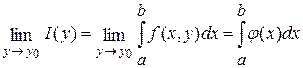 (2) (2)
Доказательство.
Непрерывность 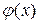 следует из теоремы 2, значит, она интегрируема на отрезке следует из теоремы 2, значит, она интегрируема на отрезке 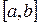 . В силу равномерной сходимости . В силу равномерной сходимости  к к 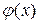 выполняется выполняется 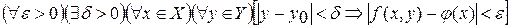 . Тогда при тех же . Тогда при тех же 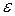 и и  имеем: имеем:
 откуда следует откуда следует 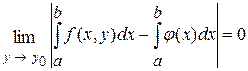 , что доказываетформулу (2). , что доказываетформулу (2).
Замечание 3.
Равенство (2) можно записать и в другом виде
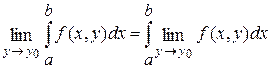 . (2`) . (2`)
Следствие 1.
Если функция  при постоянном при постоянном  непрерывна по непрерывна по 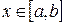 и при возрастании и при возрастании  стремится, монотонно возрастая, к непрерывной предельной функции стремится, монотонно возрастая, к непрерывной предельной функции 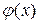 , то справедливы формулы (2) и (2`). , то справедливы формулы (2) и (2`).
В предположении, что область 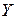 представляет собой конечный промежуток представляет собой конечный промежуток  , рассмотрим вопрос о непрерывности функции , рассмотрим вопрос о непрерывности функции 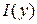 . .
Пример
(№3713 (в)). Найти 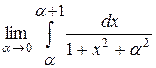 . .
1. функция 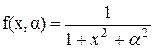 непрерывная функция на непрерывная функция на 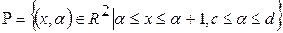 . Функции . Функции 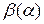 и и 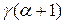 также непрерывны на также непрерывны на 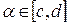 . .
2. 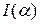 непрерывная функция (т.4 и сл.2) в промежутке непрерывная функция (т.4 и сл.2) в промежутке  , значит , значит 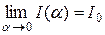
3. 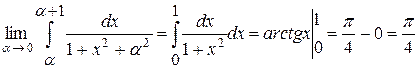 . .
Теорема 4 (о непрерывности интеграла как функции параметра).
Пусть функция  определена и непрерывна в прямоугольнике определена и непрерывна в прямоугольнике 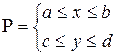 , тогда интеграл , тогда интеграл 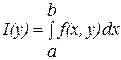 будет непрерывной функцией от параметра будет непрерывной функцией от параметра  в промежутке в промежутке  . .
Доказательство.
Так как  непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на данном прямоугольнике непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на данном прямоугольнике 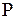 . Возьмем любое . Возьмем любое 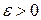 и зафиксируем и зафиксируем 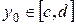 . Тогда нашему значению . Тогда нашему значению 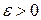 будет соответствовать будет соответствовать 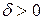 , такое, что для любых двух точек , такое, что для любых двух точек 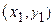 , , 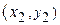 принадлежащих принадлежащих 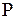 , из неравенств , из неравенств 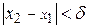 и и 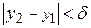 , будет следовать , будет следовать 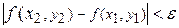 . Положим . Положим 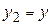 , , 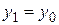 , где , где  , ,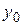 - любые из - любые из  , и , и 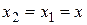 , где , где 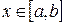 . Тогда получим . Тогда получим
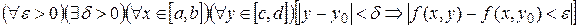 . Это означает, что функция . Это означает, что функция  равномерно стремится к равномерно стремится к 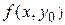 . В таком случае по теореме 3 . В таком случае по теореме 3 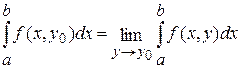 , а уже отсюда следует равенство , а уже отсюда следует равенство 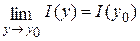 , то есть наша функция , то есть наша функция 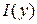 непрерывна на непрерывна на  . .
Замечание 4.
Совершенно аналогично доказывается теорема для 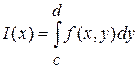 , где , где 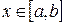 . .
Следствие 2.
Если  непрерывна на прямоугольнике непрерывна на прямоугольнике 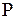 , то , то 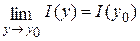 . .
Пример
. Найти 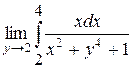 . .
1. 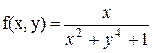 непрерывна на непрерывна на 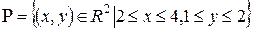
2. тогда по теореме 4. и следствию 2 получаем
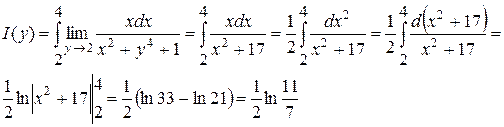
Пункт 3. Дифференцирование под знаком интеграла
При изучении свойств функции 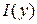 важное значение имеет вопрос о ее производной по параметру. Вычислить производную можно по формуле важное значение имеет вопрос о ее производной по параметру. Вычислить производную можно по формуле 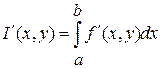 , которую вывел Лейбниц 1697. Рассмотрим теорему, устанавливающую простые достаточные условия для применимости этой формулы. , которую вывел Лейбниц 1697. Рассмотрим теорему, устанавливающую простые достаточные условия для применимости этой формулы.
Реклама

Теорема (о дифференцировании интеграла, зависящего от параметра).
Пусть функция  определена и непрерывна в прямоугольнике определена и непрерывна в прямоугольнике 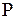 и имеет там непрерывную частную производную и имеет там непрерывную частную производную 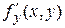 . Пусть . Пусть 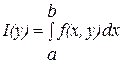 , , 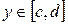 . Тогда: . Тогда:
1. функция 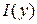 имеет в промежутке имеет в промежутке  производную производную 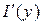 ; ;
2. 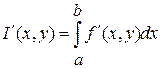 , то есть , то есть 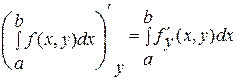 , , 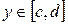 . .
Доказательство.
Возьмем любую точку 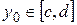 и зафиксируем ее. Придадим и зафиксируем ее. Придадим 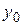 приращение приращение 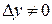 и точка и точка 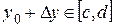 . Тогда . Тогда 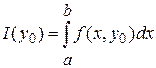 , , 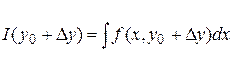 , ,
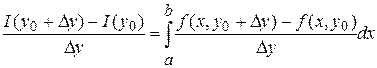 (1) (1)
По теореме Лагранжа 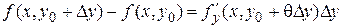 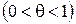 . Следовательно, . Следовательно,
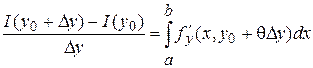 . (2) . (2)
Переходя в (2) к пределу при 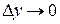 , приняв во внимание теорему о допустимости предельного перехода под знаком интеграла, получим: , приняв во внимание теорему о допустимости предельного перехода под знаком интеграла, получим:
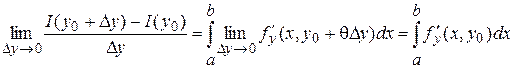 . .
Из этого следует, что 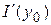 существует, причем существует, причем 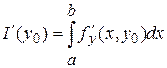 . Так как . Так как 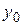 - любое - любое  , то , то 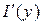 существует для любого существует для любого 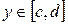 , причем , причем 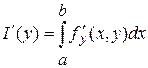 . .
Пример.
Найти производную 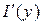 функции функции 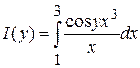 . .
1. 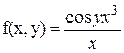 непрерывна на непрерывна на 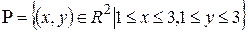
2. 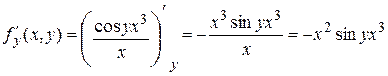 . Эта функция также непрерывна на . Эта функция также непрерывна на 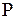 . .
3.
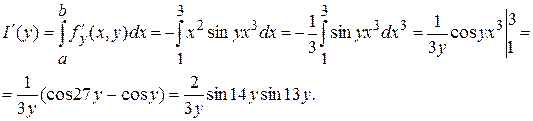
4. 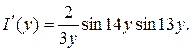
Пункт 4. Интегрирование по параметру под знаком интеграла
Рассмотрим вопрос об интегрировании по параметру  функции функции 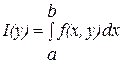 . Если она интегрируема, то интеграл будет иметь вид . Если она интегрируема, то интеграл будет иметь вид 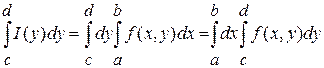 . Достаточное условие для равенства двух повторных интегралов дает следующая теорема. . Достаточное условие для равенства двух повторных интегралов дает следующая теорема.
Теорема.
Если  непрерывная по обеим переменным функция на прямоугольнике непрерывная по обеим переменным функция на прямоугольнике 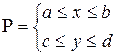 , то , то 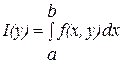 интегрируемая на промежутке интегрируемая на промежутке  функция и справедливо равенство функция и справедливо равенство 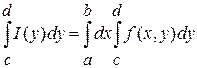 , то есть , то есть 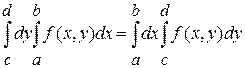 . .
Также можно расписать с помощью повторных интегралов следующим образом 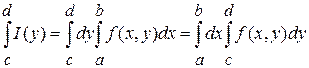 . .
Докажем более общее равенство.
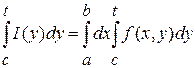 для любого для любого 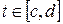 . (1) . (1)
В левой и правой частях равенства (1) мы имеем две функции от параметра t
. Вычислим их производные по t
. Так как 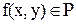 , то , то 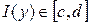 (т.4 п.2), а следовательно (т.4 п.2), а следовательно 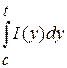 есть интеграл с переменным верхним пределом от непрерывной функции. Тогда по теореме Барроу: есть интеграл с переменным верхним пределом от непрерывной функции. Тогда по теореме Барроу:
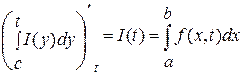 , , 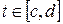 . (2) . (2)
В правой части стоит интеграл 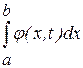 , где , где 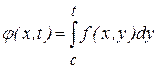 . Действительно функция . Действительно функция 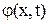 удовлетворяет условиям теоремы п.3, она также непрерывна по удовлетворяет условиям теоремы п.3, она также непрерывна по 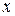 в силу теоремы 4 п.2.Мы можем найти производную в силу теоремы 4 п.2.Мы можем найти производную 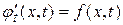 , которая будет непрерывна как функция двух переменных. , которая будет непрерывна как функция двух переменных.
Тогда по теореме о дифференцировании по параметру под знаком интеграла
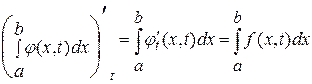 , , 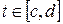 . (3) . (3)
Видим, что левая и правая части равенства (1) имеют в промежутке  совпадающие производные (см. (2) и (3)). А значит они отличаются в этом промежутке только на постоянную величину, т. е. совпадающие производные (см. (2) и (3)). А значит они отличаются в этом промежутке только на постоянную величину, т. е. 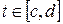 . .
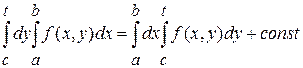 . (4) . (4)
Положив в (4) t
=
c
, получим 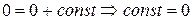 . Значит, будем иметь вместо (4) для любого . Значит, будем иметь вместо (4) для любого 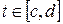
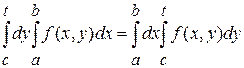 . (5) . (5)
Пусть в (5) t
=
d
, получим
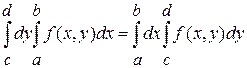 . .
Что и требовалось получить.
Глава 2. Несобственные интегралы, зависящие от параметра
Пункт 1. Равномерная сходимость несобственных интегралов, зависящих от параметра
При рассмотрении теории интегралов, зависящих от параметра, в случае несобственных интегралов особую роль играет понятие равномерной сходимости. Выясним это понятие сначала для несобственных интегралов первого рода (НИЗП-1), затем для интегралов второго рода (НИЗП-2).
Пусть функция  определена и непрерывна на некотором прямоугольнике определена и непрерывна на некотором прямоугольнике  и при любом фиксированном и при любом фиксированном 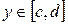 существует несобственный интеграл, зависящий от параметра, этой функции на любом промежутке существует несобственный интеграл, зависящий от параметра, этой функции на любом промежутке  . Тогда интеграл сходится и равен . Тогда интеграл сходится и равен
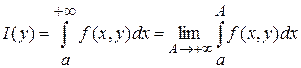 . .
В этом случае 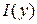 называют несобственным интегралом первого рода (НИЗП-1). называют несобственным интегралом первого рода (НИЗП-1).
Утверждение о том, что 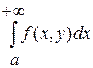 сходится при каждом сходится при каждом 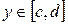 означает следующее: при каждом фиксированном означает следующее: при каждом фиксированном 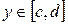
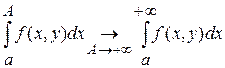 . .
Следовательно,
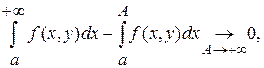 или или 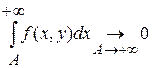 . .
Это значит, что для каждого 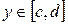 по любому по любому 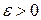 можно указать число можно указать число 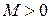 такое, что если такое, что если 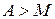 , то , то 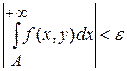 . Важно заметить, что . Важно заметить, что 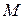 зависит и от зависит и от  ,и от ,и от 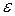 : :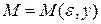 . Если же для любого . Если же для любого 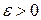 можно указать число можно указать число 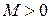 , зависящее только от , зависящее только от 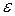 , такое, что при , такое, что при 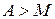 выполняется выполняется 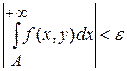 для для 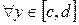 , то в этом случае , то в этом случае 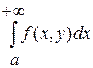 называется равномерно сходящимся относительно параметра называется равномерно сходящимся относительно параметра  . .
Теперь сформулируем критерий Коши для равномерной сходимости для нашего случая следующим образом:
Теорема 1. (критерий Коши равномерной сходимости для НИЗП-1).
Для того чтобы интеграл 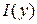 сходился равномерно по переменной сходился равномерно по переменной  на промежутке на промежутке  , необходимо и достаточно, чтобы выполнялась цепочка , необходимо и достаточно, чтобы выполнялась цепочка
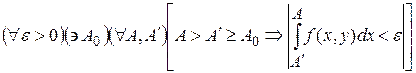 , , 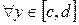 . .
Рассмотрим достаточные признаки равномерной сходимости.
Теорема 2. (признак Вейерштрасса равномерной сходимости НИЗП-1).
Пусть функция  определена и непрерывна на прямоугольнике определена и непрерывна на прямоугольнике 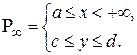 и удовлетворяет условиям: и удовлетворяет условиям:
1. непрерывна по переменной 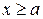 , ,
2. существует функция 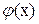 , что , что 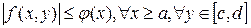 , ,
3. 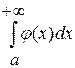 - сходится. - сходится.
Из этого следует, что 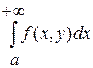 сходится равномерно по сходится равномерно по 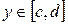 . .
Доказательство.
В соответствии с условием 3) критерия Коши о сходимости несобственных интегралов 1-го рода от функции одной переменной имеем:
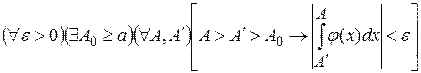 (1) (1)
Тогда при тех же 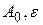 , что и в цепочке, получаем , что и в цепочке, получаем
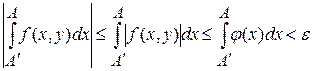 . .
А отсюда по теореме 1 следует равномерная сходимость интеграла  . .
Ч. т. д.
Замечание.
При выполнении условий теоремы 2 говорят, что функция  имеет интегрируемую мажоранту имеет интегрируемую мажоранту 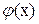 или что интеграл или что интеграл 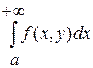 мажорируется сходящимся интегралом мажорируется сходящимся интегралом 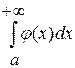 . .
Следствие.
Пусть выполняются следующие условия:
1. функция 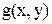 определена и непрерывна по определена и непрерывна по 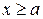 ; ;
2. функция 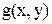 ограничена на прямоугольнике ограничена на прямоугольнике 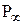 ; ;
3. интеграл 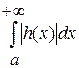 сходится, тогда следует, что сходится, тогда следует, что 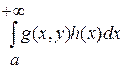
сходится равномерно по 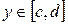 . .
Обозначим через 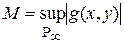 и возьмем в качестве и возьмем в качестве 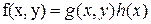 , а в качестве функции , а в качестве функции 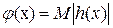 . Тогда, исходя из теоремы 2, получим цепочку (1). . Тогда, исходя из теоремы 2, получим цепочку (1).
Совершенно аналогично вводится понятие равномерной сходимости несобственных интегралов второго рода (НИЗП-2).
Пусть функция  определена в области определена в области 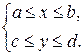 (a,b,c – конечные числа). Пусть при (a,b,c – конечные числа). Пусть при 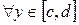 несобственный интеграл несобственный интеграл 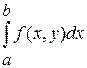 сходится. В этом случае сходится. В этом случае 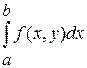 будет представлять собой функцию переменной (параметра) будет представлять собой функцию переменной (параметра)  , определенную в промежутке , определенную в промежутке  . Утверждение, что несобственный интеграл . Утверждение, что несобственный интеграл 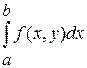 сходится при сходится при 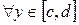 , означает следующее. При каждом фиксированном , означает следующее. При каждом фиксированном 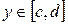 интеграл интеграл
 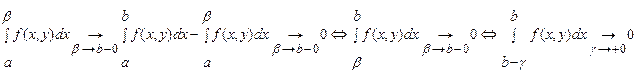 (здесь (здесь 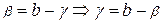 ). Это значит, что для каждого ). Это значит, что для каждого  из из  по любому по любому можно указать можно указать  такое, что при условии такое, что при условии 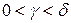 выполняется выполняется 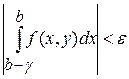 . Важно отметить, что число . Важно отметить, что число 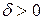 выбирается по выбирается по 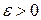 , и для каждого , и для каждого 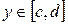 оно будет своим, другими словами, оно будет своим, другими словами, 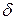 зависит и от зависит и от 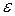 , и от , и от  : : 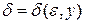 . Если же можно указать такое . Если же можно указать такое 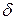 , зависящее только от , зависящее только от 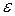 , такое, что при выполнении условия , такое, что при выполнении условия 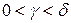 будет верно будет верно 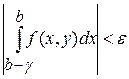 сразу для всех сразу для всех 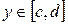 , несобственный интеграл , несобственный интеграл 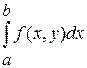 называется равномерно сходящимся относительно параметра.
Короче говорят, интеграл называется равномерно сходящимся относительно параметра.
Короче говорят, интеграл 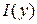 называется равномерно сходящимся по переменной называется равномерно сходящимся по переменной  на на  , если он сходится при , если он сходится при 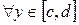 и выполняется цепочка и выполняется цепочка 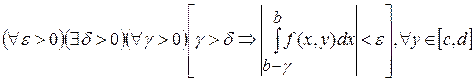 . .
Для НИЗП-2 справедливы теоремы аналогичные т.1 и т. 2.
Теорема 3. (критерий Коши равномерной сходимости НИЗП-2).
Для того чтобы НИЗП-2 равномерно сходился по 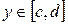 необходимо и достаточно, чтобы: необходимо и достаточно, чтобы:
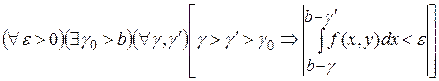 , , 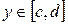 . .
Теорема 4.
Пусть функция  определена в области определена в области 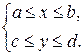  и удовлетворяет следующим условиям: и удовлетворяет следующим условиям:
1. функция  непрерывна по непрерывна по 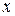 , при , при 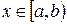 ; ;
2. существует такая функция 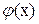 , что , что 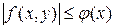 , , 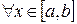 и и 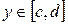 . .
3. 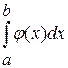 - сходится - сходится 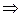
НИЗП-2 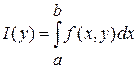 сходится равномерно по сходится равномерно по  на на  . .
Доказательство проводится аналогично доказательству теоремы 2.
Пример.
Исследовать на равномерную сходимость интеграл  . .
Для определения равномерной сходимости необходимо проверить выполнение всех условий теоремы 2.
1. 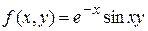 определена и непрерывна в области определена и непрерывна в области 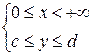 ; ;
2. существует функция 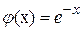 , , 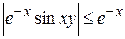 , для любого , для любого 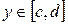 ; ;
3. 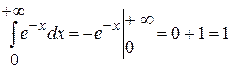 , то есть сходится. , то есть сходится.
Так как все условия выполнены, то интеграл 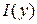 сходится равномерно относительно сходится равномерно относительно  на любом промежутке на любом промежутке  . .
Пункт 2. Непрерывность НИЗП, предельный переход под знаком интеграла.
В этом пункте мы рассмотрим предельный переход под знаком интеграла, имеющего бесконечный предел, и непрерывность интеграла как функции параметра. Условия, достаточные для допустимости предельного перехода, даются следующей теоремой:
Теорема 1.
Пусть функция  , определенная на прямоугольнике , определенная на прямоугольнике 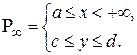 , удовлетворяет условиям: , удовлетворяет условиям:
1. функция  по по 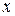 на промежутке на промежутке  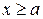 ; ;
2.  равномерно стремится к равномерно стремится к 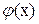 при при  по по 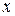 , где , где 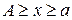 ; ;
3. интеграл 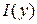 сходится равномерно по сходится равномерно по  на на  . .
В результате справедливо равенство
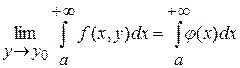 (1) (1)
Доказательство.
Функция 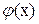 будет непрерывной. По условию равномерной сходимости для любого будет непрерывной. По условию равномерной сходимости для любого 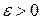 найдется такое найдется такое 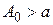 , что , что 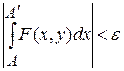 , для , для 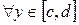 , но только , но только 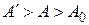 . Переходя к пределу при . Переходя к пределу при 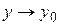 под знаком интеграла, получим под знаком интеграла, получим 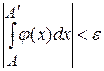 . Значит . Значит 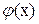 интегрируемая на бесконечном промежутке функция. Тогда при интегрируемая на бесконечном промежутке функция. Тогда при 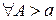 , имеем , имеем
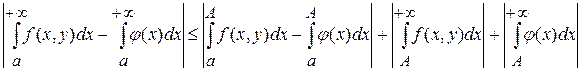 . .
Если взять произвольное число 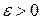 , зафиксировать число , зафиксировать число 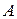 так, чтобы второе и третье слагаемые справа стали меньше так, чтобы второе и третье слагаемые справа стали меньше 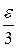 , а затем приблизить , а затем приблизить  к к 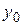 , чтобы первое слагаемое стало меньше , чтобы первое слагаемое стало меньше 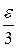 . Тогда получим . Тогда получим 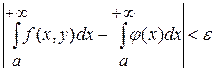 , что приводит к равенству (1). , что приводит к равенству (1).
Ч.т.д.
Следствие.
Пусть функция  неотрицательна и непрерывна по неотрицательна и непрерывна по 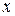 , при , при 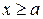 , и монотонно возрастая, стремится к , и монотонно возрастая, стремится к 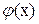 с возрастанием с возрастанием  . Если функция . Если функция 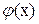 непрерывна и интегрируема на промежутке непрерывна и интегрируема на промежутке 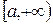 , то справедлива формула (1). , то справедлива формула (1).
Простым следствием из теоремы 1 является теорема о непрерывности интеграла по параметру.
Теорема 2.
Пусть функция  определена и непрерывна для значений определена и непрерывна для значений 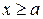 и значений и значений 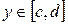 . Если . Если 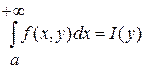 сходится равномерно относительно сходится равномерно относительно  на на  , тогда , тогда 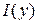 - непрерывная функция от параметра - непрерывная функция от параметра  в этом промежутке. в этом промежутке.
Доказательство (аналогично теореме для собственных интегралов).
По теореме Кантора при 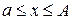 и и 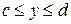 функция функция  равномерно непрерывна, а значит если равномерно непрерывна, а значит если 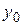 - это любое фиксированное из - это любое фиксированное из  значение, то наша функция равномерно, относительно значение, то наша функция равномерно, относительно 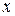 , стремится к , стремится к 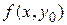 при при 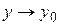 . Так как . Так как 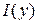 сходится равномерно, то по т.1 следует сходится равномерно, то по т.1 следует
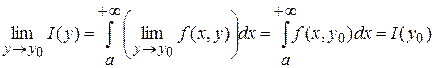 , ,
значит интеграл 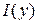 - непрерывная функция. - непрерывная функция.
Пункт 3. Интегрирование по параметру НИЗП
Чтобы выяснить интегрируема ли функция 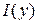 по параметру, необходимо рассмотреть следующую теорему. по параметру, необходимо рассмотреть следующую теорему.
Теорема 1.
Пусть функция  определена и непрерывна, как функция от двух переменных, в множестве определена и непрерывна, как функция от двух переменных, в множестве 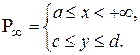 Если интеграл Если интеграл 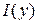 сходится равномерно по сходится равномерно по  на на  , то справедлива формула , то справедлива формула
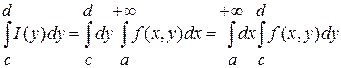 . (1) . (1)
Доказательство.
При любом 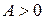 выполняется равенство выполняется равенство
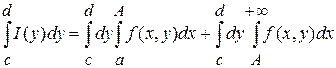 . (2) . (2)
Так как функция  непрерывна при непрерывна при 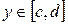 и и 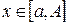 , по теореме о непрерывности интеграла как функции параметра следует, что , по теореме о непрерывности интеграла как функции параметра следует, что
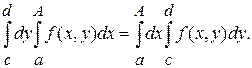 (3) (3)
Тогда из (2) 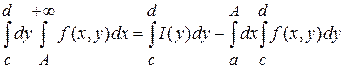 . .
Так как 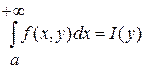 сходится равномерно, то при произвольном сходится равномерно, то при произвольном 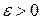 будет будет 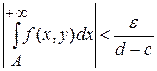 . В результате этого оценим левую часть (3) по модулю: . В результате этого оценим левую часть (3) по модулю:
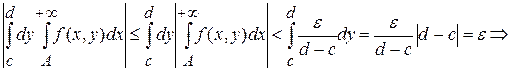
в силу (3) 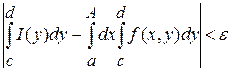 . Последнее означает, что . Последнее означает, что
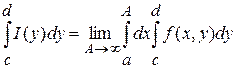 . .
Так как левая часть существует в этом равенстве, то по определению несобственных интегралов правая часть также существует, причем равная 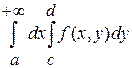 . То есть справедлива формула (1). . То есть справедлива формула (1).
Ч.т.д.
Следствие.
Если непрерывная функция  неотрицательная при неотрицательная при 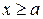 и интеграл и интеграл 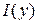 непрерывен по непрерывен по 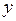 на на  , то имеет смысл формула (1). , то имеет смысл формула (1).
Таким образом, мы установили право переставлять два интеграла, из которых один распространен на бесконечный промежуток, а другой – на конечный. Очень часто приходится переставлять интегралы, взятые в бесконечных промежутках по формуле 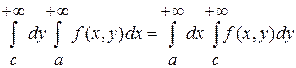 . .
Чаще всего такую перестановку сложно проделать.
Теоремы 2.
Пусть функция неотрицательна и непрерывна при 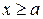 , , 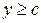 , интегралы , интегралы 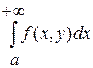 и и 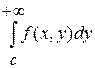 (*) существуют и являются непрерывными функциями по переменным соответственно. Тогда, если существует один из интегралов, то существует и второй, причем они равны между собой. (*) существуют и являются непрерывными функциями по переменным соответственно. Тогда, если существует один из интегралов, то существует и второй, причем они равны между собой.
Замечание.
Интегралы (*) будут заведомо интегрированы, если они равномерно сходятся по  и и 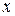 соответственно. соответственно.
Пример.
Проинтегрируем функцию  . .
Имеем  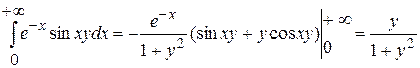 . Все условия т. 2 п. 2 выполняются. Положим . Все условия т. 2 п. 2 выполняются. Положим 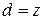 , где , где 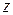 - любое конечное число. По теореме т. 1 п. 3 - любое конечное число. По теореме т. 1 п. 3
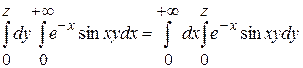 . .
Следовательно, интегрируя обе части равенства по  от 0 до от 0 до 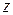 , будем иметь , будем иметь
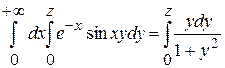 . .
Но 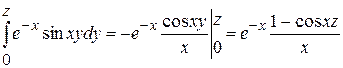 (это равенство установлено для (это равенство установлено для 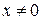 ; оно верно и при ; оно верно и при 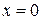 , если в этой точке понимать его в предельной). В том случае для любого конечного , если в этой точке понимать его в предельной). В том случае для любого конечного 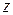 примет вид: примет вид:
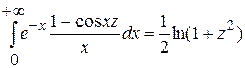 . .
Пункт 4. Дифференцирование НИЗП по параметру
Теорема 1.
Пусть функция  определена и непрерывна по определена и непрерывна по 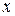 на промежутке на промежутке 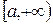 , , 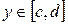 . Она имеет там непрерывную частную производную . Она имеет там непрерывную частную производную 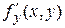 , интеграл , интеграл 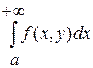 сходится при каждом сходится при каждом 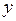 на на  , а , а  сходится равномерно. Тогда справедлива формула сходится равномерно. Тогда справедлива формула
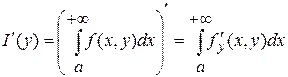 . (*) . (*)
Доказательство.
Так как 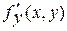 непрерывна и непрерывна и  сходится равномерно относительно сходится равномерно относительно  на на  , то для нее, в силу т. 3 п. 3, выполняется формула (1) пункта 3. Заменим в формуле (1) , то для нее, в силу т. 3 п. 3, выполняется формула (1) пункта 3. Заменим в формуле (1)  и получим: и получим:
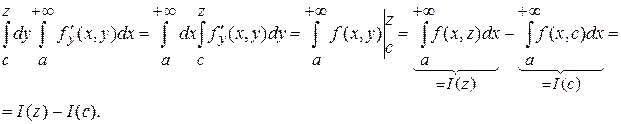
Откуда 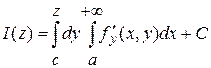 . Производная правой части последнего равенства существует и равна . Производная правой части последнего равенства существует и равна 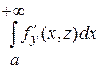 , значит существует производная и у левой части, причем , значит существует производная и у левой части, причем 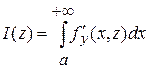 . Это равенство установлено для . Это равенство установлено для 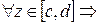 , что выполняется формула (*). , что выполняется формула (*).
Ч.т.д.
|