|
Санкт-Петербургский государственный университет сервиса и экономики
Кафедра «Управление предпринимательской деятельностью»
Контрольная работа
по дисциплине «Системный анализ
в сервисе»
Выполнила студентка
0608 группы 3 курса
Анцупова М.М.
Санкт-Петербург
2011
Вариант 1.
ЗАДАНИЕ 1. Классификация систем
Провести классификацию объектов из приложения 1, согласно варианту, занести результаты в таблицы 1.1−1.3 (проставив номера объектов в соответствующие клетки).
Таблица 1.1 Классификация систем по степени сложности и обусловленности действия
| По степени сложности
|
Простые
|
Сложные
|
Очень сложные
|
| По обусловленности действия
|
| Детерминированные
|
55
|
57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98
|
1, 3, 4, 5, 6, 7, 10, 11, 12, 15, 45,
|
| Вероятностные
|
13, 37, 46,
|
8, 9, 17, 19, 21, 22, 24, 25, 26, 27, 28, 29, 30, 31, 34, 35, 36, 38, 39, 40, 42, 47, 49, 50, 51, 52, 56
|
2, 14, 16, 18, 20, 23, 32, 33, 41, 43, 44, 48, 53, 54, 99, 100
|
Таблица 1.2 Классификация систем по происхождению и характеру поведения
| По происхождению
|
Искусственные
|
Естественные
|
| По характеру поведения
|
| Целенаправленные
|
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 21, 22, 23, 24, 25, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100
|
| Адаптивные
|
26,
|
20, 44,
|
Таблица 1.3
| По сущности
|
Технические
|
Биологические
|
Социально-экономические
|
| По внешнему поведению
|
| Открытые
|
1, 3, 4, 5, 6, 9, 10, 17, 18, 24, 25, 27, 28, 30, 32, 34, 35, 37, 39, 42, 46, 50, 51, 55, 57, 58, 65, 67, 70, 71, 73, 78, 79, 80, 81, 82, 83, 84, , 86, 87, 88, 89, 90, 91, 92, 93, 95, 96, 98
|
20, 44
|
2, 7, 8, 11, 12, 13, 14, 15, 16, 19, 21, 22, 23, 29, 31, 33, 36, 38, 39, 40, 41, 42, 43, 45, 47, 48, 49, 52, 53, 54, 56, 59, 60, 61, 62, 63, 64, 66, 68, 69, 72, 73, 74, 75, 76, 77, 99, 100
|
| Замкнутые (относительно)
|
94
|
26
|
85, 88, 93, 97
|
Поскольку абсолютно замкнутых систем не существует в таблицу заносятся системы, замкнутые по отношению к материальным, информационным или энергетическим параметрам входа и выхода.
ЗАДАНИЕ 2. Составление анкеты для получения
экспертных оценок
Проходит презентация нового туристского продукта. Взять интервью у разработчика этой программы.
1. Важно ли присутствие на презентации руководства турфирмы?
2. Влияет ли на успешность презентации костюм ведущего?
3. Изложите использованные методы презентации?
4. Как прошла презентация?
5. Какие методы презентации самые эффективные?
6. Какие трудности в презентации тура?
7. Какие финансовые результаты ожидаются от реализации нового туристского продукта?
8. Какие формы продвижения нового туристского продукта более выгодны?
9. Каков маркетинговый бюджет нового туристского продукта?
10. Какой вопрос, заданный вам на презентации, запомнился больше всего?
11. Какую долю рынка рассчитываете получить?
12. На сколько новый продукт отличается от предыдущей модели?
13. На сколько чаще будут проводиться презентации?
14. Назовите сумму затрат на презентацию?
15. Назовите целевую аудиторию нового туристского продукта?
16. Насколько влияет на успех презентации пол и возраст ведущего?
17. Насколько публика была внимательна?
18. Опишите конкурентные преимущества нового туристского продукта?
19. Сколько времени должна длиться презентация?
20. Что не удалось в презентации тура?
ЗАДАНИЕ 3. Построение дерева целей
Перед менеджером по работе с персоналом стоит задача: Как в краткосрочной перспективе поднять заработную плату персоналу. Составить дерево целей из 3-х уровней.
| Повышение зарплаты персоналу
|
| Сократить персонал на 10%
|
Увеличить объем реализации
|
Увеличить фонд заработной платы
|
| 
|
| Провести консультации с директором по персоналу
|
Согласовать сокращение персонала с возможностью повышения производительности труда
|
Провести консультации с директором по производству
|
Исследовать рынок
|
Провести консультации с партнерами по бизнесу
|
Провести консультации с партнерами по бизнесу
|
Провести общее собрание акционеров
|
Провести консультации с коммерческим директором
|
|
|
| Согласовать сокращение персонала с возможностью повышения производительности труда
|
Выполнить условия коллективного договора
|
Изучить возможности повышения производительности труда
|
Изучить возможности повышения реализации
|
Изучить возможности кооперации
|
ЗАДАНИЕ 4. Применение метода экспортных оценок.
Процедура многомерного выбора
Оценки показателей каждым из опрошенных экспертов
Таблица 4.1
| Показатели
|
Эксперты
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| е1
|
2
|
9
|
5
|
6
|
6
|
9
|
9
|
1
|
10
|
1
|
| е2
|
5
|
7
|
9
|
5
|
9
|
1
|
3
|
1
|
5
|
3
|
| е3
|
6
|
6
|
5
|
9
|
5
|
6
|
2
|
5
|
5
|
5
|
| е4
|
8
|
3
|
3
|
1
|
2
|
4
|
1
|
6
|
2
|
4
|
| е5
|
10
|
2
|
4
|
8
|
2
|
5
|
5
|
9
|
8
|
8
|
| е6
|
9
|
1
|
8
|
7
|
5
|
4
|
10
|
6
|
8
|
7
|
Требуется обосновать сравнение между объектами и выбрать наилучший из них.
Задача состоит в выборе наиболее значимого элемента еi
или группы этих элементов при разных предположениях относительно требований к точности совпадения мнений всех экспертов.
E = { еi
} i = 1,6
К = К1
К2
…...К10
Оценки рассматриваемых показателей каждым из опрашиваемых экспертов
αК
j
, i = 1,2…6 К = 1,2….10 совпадают с данными таблицы 4.1.
Теперь построим матрицу соответствия.
С этой целью для каждой пары объектов (еi
,еj
) определим коэффициенты соответствия сij
, исходя из предположения, что объект еi
предпочтительнее еj...
Результаты расчётов представлены следующей матрицей С (табл. 4.2).
Таблица 4.2
Матрица С
| еj
|
еi
|
| е1
|
е2
|
е3
|
е4
|
е5
|
е6
|
|  е1
|
С12
= 0,6
|
0,6
|
0,7
|
0,6
|
0,4
|
|
е2
|
0,4
|
|
0,5
|
0,6
|
0,3
|
0,3
|
| е3
|
0,4
|
0,5
|
|
0,8
|
0,5
|
0,4
|
| е4
|
0,3
|
0,4
|
0,2
|
|
0,2
|
0,3
|
| е5
|
0,4
|
0,7
|
0,5
|
0,8
|
|
0,7
|
| е6
|
0,6
|
0,7
|
0,6
|
0,7
|
0,3
|
|
Расчет коэффициента С12
.
Выдвигаем гипотезу, что е1
предпочтительнее е2.
Это предположение разделяют экспертов. Множество критериев, соответствующих этому предположению, С12
имеют номера: К = 2, 3, 4, 5, 6, 8. Следовательно
С12
= 
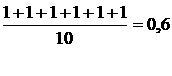
Аналогично рассчитываются значения остальных элементов матрицы С.
После построения матрицы соответствия С нужно рассчитать значение элементов матрицы несоответствия Д.
Элемент матрицы несоответствия Д учитывает те критерии, по которым существует противоречие вынесенной гипотезе, что объект е1
предпочтительнее объекта е2.
Для расчёта необходимо:
Для пары объектов ( еi
,еj
) показатель dij
(1) рассчитывается следующим образом:
Выделяется множество экспертов, оценки которых противоречат выдвинутой гипотезе, что объект е1
предпочтительнее объекта е2.
К = 1, 3, 5, 10.
Для этих критериев рассчитаем разность оценок объектов е1
и е2
— величину несоответствия.
[α1
2
- α1
1
] = 3.
[α3
2
- α3
1
] = 4.
[α5
2
- α5
1
] = 3.
[α10
2
- α10
1
] = 2.
Полученные величины упорядочиваются в порядке невозрастания: [4, 3, 3, 2]
3. Показатель несоответствия d12
(1) = 
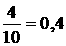вычисляется как отношение первого члена последовательности из п.2 к масштабу шкалы.
Матрица Д (1)имеет вид
| |
е1
|
е2
|
е3
|
е4
|
е5
|
е6
|
| е1
|
|
d12
(1) = 0,4
|
0,6
|
0,5
|
0,8
|
0,6
|
|
е2
|
0,4
|
|
0,4
|
0,3
|
0,4
|
0,2
|
| е3
|
0,7
|
0,5
|
|
0,6
|
0
|
1
|
| е4
|
0,5
|
0,5
|
0,5
|
|
0,5
|
0,8
|
| е5
|
0,2
|
0,7
|
0,7
|
0,8
|
|
0,4
|
| е6
|
0,8
|
0,6
|
0,5
|
0,2
|
0,6
|
|
Данные матриц С и Д (s) позволяют построить графы сравнения объектов при различных требованиях к порогам соответствия и несоответствия и выделить ядро соответствующего графа.
Рассмотрим, как изменяются графы в зависимости от значения параметров (c, d, s).
Пусть s = 1, С = 0,7, d = 0,3. Тогда можно провести сравнение только для двух объектов — е3
и е1.
Ядро графа включает пять элементов íе1
е2
е4
е5
е6
ý.
Другими словами, эти объекты при указанных требованиях к совпадению мнений экспертов не сравнимы между собой. При этом объект е1
признаётся более значимым, чем объект (показатель) е3.
Снижение требований к порогу соответствия С = 0,6 приводит к дополнительной возможности сравнения показателей е2
и е1
. (рис б). Следовательно, ядро этого графа содержит теперь элементы íе2
е4
е5
е6
ý..
При s = 2 и тех же порогах соответствия и несоответствия (С = 0,8, d = 0,3) граф содержит единственный элемент (показатель), превосходящий все остальные. Таким образом, показатель е5
может быть принят в качестве основного при решении данной проблемы с указанной степенью риска, отраженной набором оценок степени согласованности мнений экспертов. Точно так же введение более строгих требований к порогу несоответствия (уменьшение значения d с 0,3 до 0,2) приводит к введению в ядро графа элемента е6
. Исследование изменений ядер графов в зависимости от изменения требований к параметрам согласования различных критериев (различных мнений экспертов) позволяет упорядочить рассматриваемые объекты.
ЗАДАНИЕ 5. Оценка сложных систем в условиях
риска и неопределенности
В ресторане решено делать бизнес-ланч.
Процесс производства позволяет изготавливать 70, 120 или 150 бизнес-ланчей. Число посетителей колеблется от 60 до 160. Необходимо определить число изготавливаемых бизнес-ланчей аi
, если число посетителей kj
.
Матрица эффективности имеет вид (руб).
Матрица эффективности
| а/к
|
к1
= 60
|
к2
= 95
|
к3
= 125
|
к4
= 160
|
| а1
= 70
|
-1600
|
2300
|
2300
|
2300
|
| а2
= 120
|
-4000
|
5300
|
7800
|
7800
|
| а3
= 150
|
-6200
|
-1750
|
10000
|
9500
|
1. Критерий среднего выигрыша. Предполагает задание вероятностей состояния обстановки Рi
. Эффективность систем оценивается как среднее ожидание (мат. ожидание) оценок эффективности по всем состояниям обстановки.
Оптимальной системе будет соответствовать максимальная оценка.
К = ∑ Рi
∙ к ij
Определим частоту каждого кi
:
Р1
= 0,14; Р2
= 0,22; Р3
= 0,28; Р4
= 0,36.
Определим оценку:
К(а1
) = 0,14 ∙ (-1600) + 0,22 ∙ 2300 + 0,28 ∙ 2300 + 0,36 ∙ 2300 = 1768,18.
К(а2
) = 0,14 ∙ (-4000) + 0,22 ∙ 5300 + 0,28 ∙ 7800 + 0,36 ∙ 7800 = 5651,14.
К(а3
) = 0,14 ∙ (-6200) + 0,22 ∙ (-1750) + 0,28 ∙ 10000 + 0,36 ∙ 9500 = 5072,16.
Оптимальное решение — число бизнес-ланчей — а2
= 120.
2. Критерий Лапласа (достаточного основания)
Предполагается, что состояние обстановки равновероятно, так как нет достаточных оснований предполагать иное.
К = 1/к∑Кij
, для каждого i, а оптимальное значение указывает максимальную сумму К.
К(а1
) = 0,333 ∙ (-1600 + 2300 + 2300 + 2300) = 1325,0.
К(а2
) = 0,333 ∙ (-4000 + 5300 + 7800 + 7800) = 4225,0.
К(а3
) = 0,333 ∙ (-6200 + (-1750) + 10000 + 9500) = 2887,5.
Оптимальное решение — число бизнес-ланчей — а2
= 120.
3. Критерий осторожного наблюдателя (критерий Вальда). Это максимальный критерий (максимальные доходы, минимальные потери). Он гарантирует определенный выигрыш при худших условиях. Критерий использует то, что при неизвестной обстановке нужно поступать самым осторожным образом, ориентируясь на минимальное значение эффекта каждой системы.
Для этого в каждой строке матрицы находится минимальная из оценок систем
К(а
i
)
min К
ij
.
j
Оптимальной считается система из строки с максимальным значением эффективности
Копт=
max (
minKij
)
для всех ij
i
j
К(а1
) = min(-1600; 2300; 2300; 2300) = −1600.
К(а2
) = min(-4000; 5300; 7800; 7800) = −4000.
К(а3
) = min(-6200; −1750; 10000; 9500) = −6200.
Оптимальное решение — число бизнес-ланчей — а1
= 70.
В любом состоянии обстановки выбранная система покажет результат не хуже найденного максимина. Однако такая осторожность является в ряде случаев недостатком критерия.
4. Критерий пессимизма-оптимизма (критерий Гурвица). Критерий обобщенного максимина. Согласно данному критерию при оценке и выборе систем не разумно проявлять как осторожность, так и азарт. Следует принимать во внимание самое высокое и самое низкое значение эффективности и занимать промежуточную позицию. Эффективность находится как взвешенная с помощью коэффициента α сумма максимальных и минимальных оценок.
К(
ai
) = α
max
Kij
+(1- α)*
min
Kij
j
j
0 ≤ α ≤ 1
Копт =
max { α
max
Kij
+(1+ α)*
min
Kij
}
i
j
j
d = 0,6
К(а1
) = 0,6 ∙ 2300 + (1−0,6) ∙ (-1600) = 740.
К(а2
) = 0,6 ∙ 7800 + (1−0,6) ∙ (-4000) = 3080.
К(а3
) = 0,6 ∙ 10000 + (1−0,6) ∙ (-6200) = 3520.
Оптимальное решение — число бизнес-ланчей — а3
= 150.
При α = 0 критерий Гурвица сводится к критерию максимина. На практике используются значения α из интервала (0,3÷0,7).
5. Критерий минимального риска (критерий Севиджа)
Минимизирует потери эффективности при наихудших условиях. В этом случае матрица эффективности должна быть преобразована в матрицу потерь. Каждый элемент определяется как разность между максимальным и текущим значениями оценок эффективности в столбце.
∆ К
ij
=
maxKij
-
Kij
После преобразования матрицы используется критерий минимакса
, т.е. оптимального решения критерия.
K(
ai
)=
max∆ К
ij
j
Kопт=
min (
max∆ К
ij
)
i j
Матрица потерь
| а/к
|
к1
= 60
|
к2
= 95
|
к3
= 125
|
к4
= 160
|
∑к
|
| а1
= 70
|
0
|
3000
|
7700
|
7200
|
17900
|
| а2
= 120
|
2400
|
0
|
2200
|
1700
|
6300
|
| а3
= 150
|
4600
|
7050
|
0
|
0
|
11650
|
Оптимальное решение — число бизнес-ланчей — а2
= 120.
Комментарий: критерий отражает сожаления по поводу того, что выбранная система не оказалась лучшей при определении состава обстановки. Например, если выбрать число бизнес-ланчей а1
, а угрозу n3
, то сожаление, что не выбрано лучшее число бизнес-ланчей а2
составит 7700.
Таким образом, эффективность систем в неопределенных операциях может оцениваться по ряду критериев. На выбор каждого из них может влиять ряд факторов:
а) природа конкретных операций и ее цель — в одном случае допустим риск — в другом — гарантированный результат
б) причина неопределенности — закон природы — разумные действия противника
в) характер лица, принимающего решение: — склонность добиться большего, идя на риск — всегда осторожные действия
Результаты всех расчётов записываются в одну табл. 9.
Результаты
| а\к
|
к1
|
к2
|
к3
|
к4
|
Ср. выигр
|
Лапласа
|
Вальда
|
Гурвица
|
Севиджа
|
| а1
|
-1600
|
2300
|
2300
|
2300
|
1768,18
|
1325,0
|
1600
|
740
|
17900
|
| а2
|
-4000
|
5300
|
7800
|
7800
|
5651,14
|
4225,0
|
4000
|
3080
|
6300
|
| а3
|
-6200
|
-1750
|
10000
|
9500
|
5072,16
|
2887,5
|
6200
|
3520
|
11650
|
Тип критерия для выбора рационального варианта выбирается на аналитической стадии рассмотрения сложных систем. Очевидно, что по большинству критериев оптимальное решение — число бизнес-ланчей — а2
= 120, следующий по значимости вариант — число бизнес-ланчей — а3
= 150.
ЗАДАНИЕ 6. Постановка задачи математического
программирования
В трёх цехах изготавливаются два вида изделий.
aij
– загрузка j-го цеха при изготовлении изделий, %.
ci
– прибыль от одного изделия вида i, руб.
Сформулировать ЗЛП, чтобы определить, сколько изделий каждого вида следует производить при возможно полной загрузке цехов, чтобы получить максимальную прибыль. Загрузка цехов представлена в Таблице.
Таблица
Загрузка цехов
| Изделие (j)
|
№ цеха (i)
|
Цена изделия
|
| 1
|
2
|
3
|
| 1
|
5
|
3
|
4
|
488
|
| 2
|
4
|
1,2
|
5,1
|
233
|
| Максимальная загрузка
|
100%
|
100%
|
100%
|
Решение:
В соответствии с вопросом, сформулированным в задаче, в качестве переменной величины выступит объём производства изделий каждого вида. Тогда:
Х1
— объём производства изделий 1-го вида;
Х2
— объём производства изделий 2-го вида.
Постановка задачи ЛП:
488 ∙ Х1
+ 233 ∙ Х2
® мах (максимизировать совокупную прибыль от производства изделий обоих видов);
5 ∙ Х1
+ 4 ∙ Х2
£100 — ограничение на максимальную загрузку 1-го цеха;
3 ∙ Х1
+ 1,2 ∙ Х2
£ 100 — ограничение на максимальную загрузку 2-го цеха;
4 ∙ Х1
+ 5,1 ∙ Х2
£100 — ограничение на максимальную загрузку 3-го цеха;
Х1,
Х2
³ 0 — изделия должны производиться.
|
