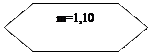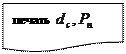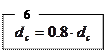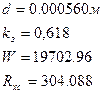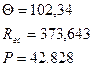| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное образовательное учреждение
высшего профессионального образования
«Чувашский государственный университет имени И.Н. Ульянова»
Электротехнический факультет
Кафедра электрических и электронных аппаратов
КУРСОВАЯ РАБОТА
по дисциплине
ТЕОРИЯ ПОДОБИЯ И МОДЕЛИРОВАНИЕ
на тему
ПРОГРАММНЫЙ КОМПЛЕКС РАСЧЕТА И МОДЕЛИРОВАНИЯ
КАТУШКИ УПРАВЛЕНИЯ
ЭЛЕКТРОМАГНИТА ПОСТОЯННОГО ТОКА
Вариант № 22
Выполнила студентка: Куприянова Л.С.
Группа ЭТ-21-02
Руководитель
: Руссова Н.В.
Чебоксары, 2005
Исходные данные.
1. Магнитодвижущая сила (МДС) обмотки управления (ОУ) 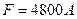 ; ;
2. Напряжение питания 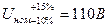 ;
;
3. Температура окружающей среды 40
°С;
4. Режим работы: длительный
;
5. Размеры поперечного сечения сердечника магнитопровода 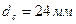 ; ;
6. Вид исполнения катушки: на гильзе
;
7. Тип обмоточного провода: ПЭВ-2.
Математическая модель обмотки управления электромагнита постоянного
тока.................................................................................................................. 4
Алгоритмы и программа расчета обмотки управления............................... 9
Расчет минимальных размеров обмотки управления................................. 17
Эскиз катушки управления........................................................................... 18
Расчет и выбор диаметра провода из стандартного ряда. Расчет параметров
ОУ в холодном состоянии............................................................................ 19
Расчет температуры нагрева ОУ. Расчет параметров ОУ в горячем
состоянии....................................................................................................... 19
Исследование зависимости потребляемой мощности ОУ от размеров
поперечного сечения сердечника магнитопровода (- 20%..+ 50% от заданного)
для МДС ОУ F
=const
,
температура нагрева ОУ Q=Qдоп
............................. 20
Исследование зависимости потребляемой мощности и температуры нагрева
ОУ от размеров поперечного сечения обмотки управления (l
/h
=1..10) для
МДС ОУ F
=const
,
обмоточное окно Q
=const
............................................... 22
Заключение.................................................................................................... 24
Реклама

Список использованной литературы........................................................... 25
Обмотки являются составной частью всех электромагнитов. Проходящий по обмотке управления (ОУ) ток создает магнитодвижущую силу (МДС), необходимую для возбуждения магнитного потока. Величина требуемой МДС определяется из расчета магнитной цепи.
Задача расчета ОУ заключается в том, чтобы получить такие обмоточные данные (диаметр провода d
, число витков W
и сопротивление обмотки R
), которые при заданном напряжении или токе обеспечивают необходимую МДС. При этом обмоточные данные и габариты ОУ выбираются таким образом, чтобы в процессе работы температура ОУ Q не превышала допустимого значения Qдоп
: 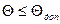 . .
Превышение t температуры Q ОУ над температурой окружающей среды Q0
рассчитывается по формуле Ньютона:
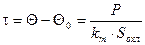 , (1) , (1)
где Р
- мощность тепловых потерь, Вт; k
т
- коэффициент теплоотдачи, Вт/(м2
×°С); S
– площадь поверхности охлаждения, м2
. Мощность тепловых потерь для случая постоянного тока
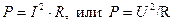 , ,
где I
, U
и R
– ток, напряжение и сопротивление ОУ.
Минимальные размеры ОУ находятся из условия допустимого нагрева обмоточного провода по формуле:
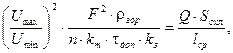 (2) (2)
где Umax
, Umin
- максимальное и минимальное значения напряжения питания, В; F
– магнитодвижущая сила ОУ, А; ρгор
- удельное сопротивление материала провода ОУ в нагретом состоянии, Ом×м; n
- коэффициент перегрузки по мощности; tдоп
=(Qдоп
-Q0
) - допустимое превышение температуры ОУ, °С; kз
- коэффициент заполнения обмоточного провода; Q
- обмоточное окно, м2
; lср
- средняя длина витков ОУ. Данное выражение получается путем преобразования формулы Ньютона (1). Левая часть (2) характеризует мощность, выделяющуюся в ОУ; правая часть – теплоотдающую способность ОУ.
Все применяемые на практике ОУ катушек электрических аппаратов могут быть сведены к расчетной модели, представленной на рис.1, где l
и h
- длина и толщина ОУ. Внутренний размер ОУ 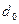 - определяются поперечным сечением магнитопровода, конструкцией каркаса и является известным. - определяются поперечным сечением магнитопровода, конструкцией каркаса и является известным. Величины, входящие в левую часть выражения (2), кроме коэффициента k
т
, также известны.
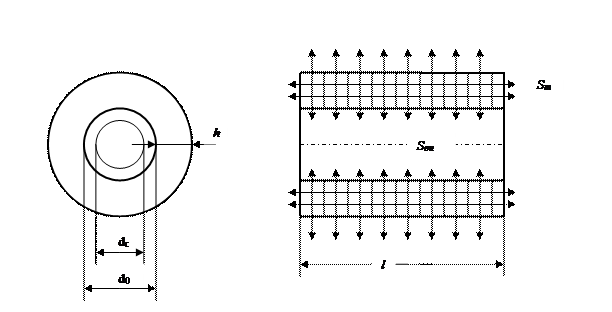
Рис. 1 - Расчетная модель обмотки управления
Коэффициент теплоотдачи зависит от температуры Q и площади охлаждаемой поверхности S
охл
:
для 10-4
м2
£ 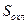 £ 10-2
м2 £ 10-2
м2
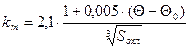 , Вт/(м2
×°С), (3) , Вт/(м2
×°С), (3)
для 10-2
м2
< 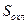 £ 0,5 м2 £ 0,5 м2
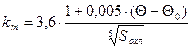 , Вт/(м2
×°С). (4) , Вт/(м2
×°С). (4)
Правая часть выражения (2) называется геометрическим параметром ОУ. Величины Q
, S
охл
и l
ср
являются функциями от длины l
и толщины h
ОУ.
Обмоточное окно ОУ
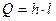 . (5) . (5)
Эквивалентная поверхность охлаждения ОУ
Реклама

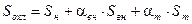 , (6) , (6)
где S
н
,
S
вн
,
S
т
- площади наружной, внутренней и торцовой поверхностей охлаждения ОУ; aвн
=k
т,вн
/k
т
, aт
=k
т,т
/k
т
, где k
т
, k
т,вн
, k
т,т
, - коэффициенты теплоотдачи с наружной, внутренней и торцовой поверхностей ОУ. Коэффициенты приведения внутренней и торцовых поверхностей к наружной поверхности aвн
,
aт
(коэффициенты эффективности теплоотдачи с внутренней и торцовых поверхностей) являются опытными данными. Вообще, расчет коэффициента теплоотдачи не только с внутренней и торцовой поверхностей, но и с наружной, представляет большие трудности. На практике пользуются эмпирическими данными значений aвн
. При этом этот коэффициент косвенно учитывает также и теплоотдачу с торцовых поверхностей ОУ (т.е. в этом случае aт
=0). Согласно литературным данным […] он составляет для:
- катушек на пластмассовом каркасе - aвн
=0;
- бескаркасных бандажированных катушек - aвн
=0,9;
- катушек намотанных на металлической гильзе - aвн
=1,7;
- катушек намотанных на сердечнике - aвн
=2,4.
В соответствии с рис.1
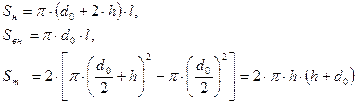
С учетом этого
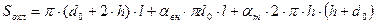 (7) (7)
Средняя длина витков ОУ
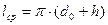 . (8) . (8)
При расчете размеров ОУ электромагнитов постоянного тока обычно задаются соотношением kl
=l
/
h
=4...8. Таким образом, входящие в выражение (2) величины k
т
, Q
, S
охл
и l
ср
можно рассматривать как функции от h
: k
т
(h
), Q
(h
), S
охл
(h
)и l
ср
(h
). С учетом этого, толщину ОУ h
можно определить решением следующего нелинейного уравнения, получаемого на основании (2):
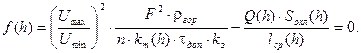 (9) (9)
Диаметр обмоточного провода при заданной МДС ОУ F
и минимально допустимом напряжении питания Umin
рассчитывается по формуле
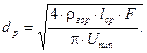 (10) (10)
Далее по сортаменту выбирается ближайший больший диаметр, находится для него коэффициент заполнения k
з
. Число витков ОУ вычисляется по формуле
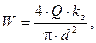 (11) (11)
где Q – площадь обмоточного окна.
Сопротивление ОУ в холодном состоянии
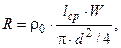 (12) (12)
где ρ0
.- удельное сопротивление материала обмоточного провода ОУ при температуре окружающей среды Q0
.
Когда размеры и параметры ОУ (катушки) определены, требуется расcчитать температуру нагрева обмотки Q и сравнить ее с допустимой температурой нагрева обмоточного провода Qдоп
. Расчет температуры нагрева ведется по формуле Ньютона (1):
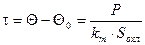 , (13) , (13)
где мощность тепловых потерь ОУ 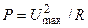 . .
Сопротивление ОУ в горячем состоянии
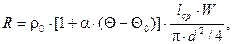 (14) (14)
где ρ0
- удельное сопротивление материала обмоточного провода ОУ при температуре окружающей среды Q0
, a - температурный коэффициент сопротивления материала обмоточного провода при температуре окружающей среды Q0
. Коэффициент теплоотдачи k
т
в выражении (13) также является функцией от температуры. С учетом этого на основании (13) получается нелинейное уравнение вида
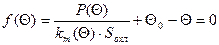 , (15) , (15)
                      



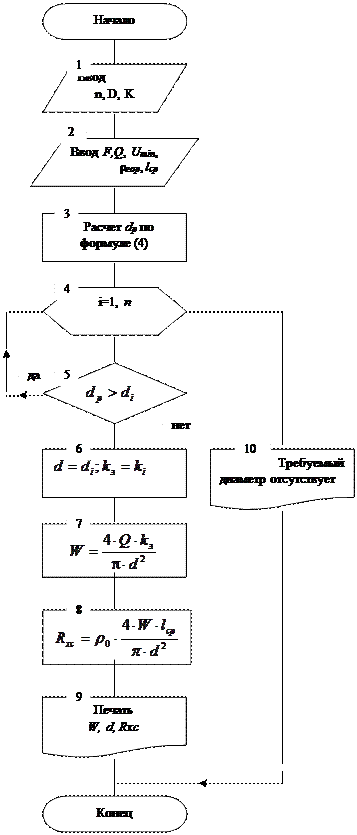
     | Рис. 2 - Алгоритм расчета обмотки управления.
|
|


 
  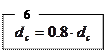  
  

 
  
Рис. 3 - Расчет минимальной толщины ОУ (а)
и коэффициента теплоотдачи (б)
Программа расчета обмотки управления.
program kr;
uses graph , crt;
const m0=4*3.1415926535897932385*0.00000010;pi=3.1415926535897932385;n1=33;
label 2,3,4,5,6,7,8,9,10,12,14,15,16,25,26,20,29;
var F,Unom,Umax,Umin,dc,e1,e2,h,Sn,km,y1,y2,dh,dx,pgor,Tdop,T0,T,T1,Ta,Tb,
kz,Q,Soxl,lcp,km1,l,n,d0,m,avn,p0,a,hnp,Svn,ha,hb,z,dp,R,W,dci,e,P,Rxc,Rgc,
t1dop,Pp,Ik:real;
D1,D,K:array[1..n1] of real; i,j:integer;
begin
clrscr;
{ishodnie dannie}
F:=4800;Unom:=110;dc:=24*0.001;Tdop:=105;T0:=40;
n:=1;Umax:=1.15*Unom;Umin:=0.9*Unom;kz:=0.5;m:=5;
avn:=1.7; p0:=1.62*0.00000001;a:=4.3*0.001; d0:=dc+0.0001;
pgor:=p0*(1+a*Tdop);
t1dop:=Tdop-T0;
{Raschet minimalnih razmerov OU metodom polovinnogo delenia}
{write('vvedite ha:= ');readln(ha);
write('vvedite hb:= ');readln(hb);}
ha:=0.001;hb:=0.100;
e1:=0.000001;e2:=0.000001; T:=Tdop;
5:
h:=ha;
l:=m*h;
Sn:=pi*(d0+2*h)*l;
Svn:=pi*d0*l;
Q:=h*l;
Soxl:= Sn+avn*Svn;
lcp:=pi*(d0+h);
if (Soxl>=0.0001) and (Soxl<=0.01) then km:=2.1*(1+0.005*(T-T0))/exp(1/3*ln(Soxl));
if (Soxl>0.01) and (Soxl<=0.5) then km:=3.6*(1+0.005*(T-T0))/exp(1/5*ln(Soxl));
if Soxl>0.5 then goto 2;
if Soxl<0.0001 then goto 3;
y1:=sqr(Umax/Umin)*sqr(F)*pgor/n/km/t1dop/kz-Q*Soxl/lcp;
h:=(ha+hb)/2;
l:=m*h;
Sn:=pi*(d0+2*h)*l;
Svn:=pi*d0*l;
Q:=h*l;
Soxl:= Sn+avn*Svn;
lcp:=pi*(d0+h);
if (Soxl>=0.0001) and (Soxl<=0.01) then km:=2.1*(1+0.005*(T-T0))/exp(1/3*ln(Soxl));
if (Soxl>0.01)and(Soxl<=0.5) then km:=3.6*(1+0.005*(T-T0))/exp(1/5*ln(Soxl));
if Soxl>0.5 then goto 2;
if Soxl<0.0001 then goto 3;
y2:=sqr(Umax/Umin)*sqr(F)*pgor/n/km/t1dop/kz-Q*Soxl/lcp;
if abs(y2)<e1 then goto 4 else begin
if y1*y2<0 then hb:=h else ha:=h;
if abs(hb-ha)<e2 then goto 4 else goto 5 end;
{Raschet i vibor diametra provoda iz standartnogo rada,raschet parametrov
OU v holodnom sostoanii}
4:
D[1]:=0.050*0.001; K[1]:=0.250; D1[1]:=0.080*0.001;
D[2]:=0.063*0.001; K[2]:=0.290; D1[2]:=0.090*0.001;
D[3]:=0.071*0.001; K[3]:=0.340; D1[3]:=0.100*0.001;
D[4]:=0.080*0.001; K[4]:=0.380; D1[4]:=0.110*0.001;
D[5]:=0.090*0.001; K[5]:=0.410; D1[5]:=0.120*0.001;
D[6]:=0.100*0.001; K[6]:=0.440; D1[6]:=0.130*0.001;
D[7]:=0.112*0.001; K[7]:=0.460; D1[7]:=0.140*0.001;
D[8]:=0.125*0.001; K[8]:=0.480; D1[8]:=0.155*0.001;
D[9]:=0.140*0.001; K[9]:=0.495; D1[9]:=0.170*0.001;
D[10]:=0.160*0.001;K[10]:=0.510;D1[10]:=0.200*0.001;
D[11]:=0.180*0.001;K[11]:=0.527;D1[11]:=0.220*0.001;
D[12]:=0.200*0.001;K[12]:=0.538;D1[12]:=0.240*0.001;
D[13]:=0.224*0.001;K[13]:=0.550;D1[13]:=0.270*0.001;
D[14]:=0.250*0.001;K[14]:=0.560;D1[14]:=0.300*0.001;
D[15]:=0.280*0.001;K[15]:=0.572;D1[15]:=0.330*0.001;
D[16]:=0.315*0.001;K[16]:=0.580;D1[16]:=0.365*0.001;
D[17]:=0.355*0.001;K[17]:=0.589;D1[17]:=0.415*0.001;
D[18]:=0.400*0.001;K[18]:=0.597;D1[18]:=0.460*0.001;
D[19]:=0.450*0.001;K[19]:=0.605;D1[19]:=0.510*0.001;
D[20]:=0.500*0.001;K[20]:=0.612;D1[20]:=0.570*0.001;
D[21]:=0.560*0.001;K[21]:=0.618;D1[21]:=0.630*0.001;
D[22]:=0.630*0.001;K[22]:=0.625;D1[22]:=0.700*0.001;
D[23]:=0.710*0.001;K[23]:=0.631;D1[23]:=0.790*0.001;
D[24]:=0.750*0.001;K[24]:=0.634;D1[24]:=0.840*0.001;
D[25]:=0.800*0.001;K[25]:=0.637;D1[25]:=0.890*0.001;
D[26]:=0.850*0.001;K[26]:=0.640;D1[26]:=0.940*0.001;
D[27]:=0.900*0.001;K[27]:=0.643;D1[27]:=0.990*0.001;
D[28]:=0.950*0.001;K[28]:=0.646;D1[28]:=1.040*0.001;
D[29]:=1.000*0.001;K[29]:=0.648;D1[29]:=1.100*0.001;
D[30]:=1.060*0.001;K[30]:=0.650;D1[30]:=1.160*0.001;
D[31]:=1.120*0.001;K[31]:=0.651;D1[31]:=1.220*0.001;
D[32]:=1.180*0.001;K[32]:=0.652;D1[32]:=1.280*0.001;
D[33]:=1.250*0.001;K[33]:=0.652;D1[33]:=1.350*0.001;
dp:=sqrt(4*pgor*lcp*F/pi/Umin);
for i:=1 to n1 do begin
if dp>D[i] then else goto 6 end;
writeln('trebuemi diametr otsutstvuet');
6:
dp:=D[i];kz:=K[i]; dci:=D1[i];
W:=4*Q*kz/pi/sqr(dp);
Rxc:=p0*(1+a*T0)*4*W*lcp/pi/sqr(dp);
Ik:=F/W;
Pp:=Ik*Unom;
{Raschet temperaturi nagreva OU metodom iteracii, raschet parametrov
OU v holodnom sostoanii}
T:=Tdop;e:=0.01;
9:
Rgc:=p0*(1+a*T)*4*W*lcp/pi/sqr(dp);
if (Soxl>=0.0001) and (Soxl<=0.01) then km1:=2.1*(1+0.005*(T-T0))/exp(1/3*ln(Soxl));
if (Soxl>0.01) and (Soxl<=0.5) then km1:=3.6*(1+0.005*(T-T0))/exp(1/5*ln(Soxl));
if Soxl>0.5 then goto 2;
if Soxl<0.0001 then goto 3;
P:=sqr(Umax)/Rgc;
T1:=T0+P/km1/Soxl;
if abs((T1-T)/T1)<e1 then goto 10 else
begin T:=T1; goto 9 end;
10:
Rgc:=p0*(1+a*T1)*4*W*lcp/pi/sqr(dp);
P:=sqr(Umax)/Rgc;
{Vivod rezultatov rascheta}
writeln('Mihimalnie razmeri OU');
writeln('h:= ',h:7:5,'; l:= ',h*m:7:5,'; Soxl:=',Soxl:7:5,'; Q:=',Q:7:5,
'; km:= ',km:5:3,' pri T=Tdop=105');
writeln ;
writeln('Diametr provoda');
writeln('dp:= ',sqrt(4*pgor*lcp*F/pi/Umin):10:7, '; d:= ',dp:10:7,'; dci:= ',dci:10:7,
'; kz:= ',kz:4:3);
writeln('Chislo witkov');
writeln('W:= ',W:10:3);
writeln('Soprotivlenie OU v xolodnom sostoanii');
writeln('Rxc:= ',Rxc:8:3);
writeln('Potreblaemaa mosnost i tok OU');
writeln('Pp:=',Pp:7:3,'; I:=',Ik:7:3);
writeln;
writeln('Temperatura nagrewa OU');
writeln('Tk:= ',T:4:2,'; km:= ',km1:5:3,' pri T=Tk');
writeln('Soprotivlenie OU v nagretom sostoanii');
writeln('Rgc:= ',Rgc:8:3);
writeln('Teplovie poteri');
writeln('P:= ',P:5:3);
{Issledovanie zavisimosti potreblaemoi mosnosti i temperaturi nagreva OU
ot razmerov poperechnogo sechenia OU (l/h=1..10) dla MDC OU F=const,
obmotochnoe okno Q=const}
readln; clrscr;
writeln('zavisimost Pp i Tk ot l/h=1..10 dla F=const Q=const');writeln;
for j:=1 to 10 do
begin
m:=j;
h:=sqrt(Q/m);
l:=m*h;
Sn:=pi*(d0+2*h)*l;
Svn:=pi*d0*l;
Soxl:= Sn+avn*Svn;
lcp:=pi*(d0+h);
if (Soxl>=0.0001) and (Soxl<=0.01) then km:=2.1*(1+0.005*(T-T0))/exp(1/3*ln(Soxl));
if (Soxl>0.01) and (Soxl<=0.5) then km:=3.6*(1+0.005*(T-T0))/exp(1/5*ln(Soxl));
if Soxl>0.5 then goto 2;
if Soxl<0.0001 then goto 3;
dp:=sqrt(4*pgor*lcp*F/pi/Umin);
for i:=1 to n1 do begin
if dp>D[i] then else goto 26 end;
26:
dp:=D[i];kz:=K[i]; dci:=D1[i];
W:=4*Q*kz/pi/sqr(dp);
Rxc:=p0*(1+a*T0)*4*W*lcp/pi/sqr(dp);
Ik:=F/W;
Pp:=Ik*Unom;
{metod iteracii}
T:=Tdop;e:=0.0001;
29:
Rgc:=p0*(1+a*T)*4*W*lcp/pi/sqr(dp);
if (Soxl>=0.0001) and (Soxl<=0.01) then km1:=2.1*(1+0.005*(T-T0))/exp(1/3*ln(Soxl));
if (Soxl>0.01) and (Soxl<=0.5) then km1:=3.6*(1+0.005*(T-T0))/exp(1/5*ln(Soxl));
if Soxl>0.5 then goto 2;
if Soxl<0.0001 then goto 3;
P:=sqr(Umax)/Rgc;
T1:=T0+P/km1/Soxl;
if abs((T1-T)/T1)<e1 then goto 20 else
begin T:=T1; goto 29 end;
20:
Rgc:=p0*(1+a*T1)*4*W*lcp/pi/sqr(dp);
if (Soxl>=0.0001) and (Soxl<=0.01) then km1:=2.1*(1+0.005*(T1-T0))/exp(1/3*ln(Soxl));
if (Soxl>0.01) and (Soxl<=0.5) then km1:=3.6*(1+0.005*(T1-T0))/exp(1/5*ln(Soxl));
if Soxl>0.5 then goto 2;
if Soxl<0.0001 then goto 3;
P:=sqr(Umax)/Rgc;
if m=5 then textcolor (red) else textcolor (white);
writeln('l/h:=',m:2:0,'; Pp:=',Pp:5:3,'; Tk:=',T:6:2,'; Q:=',Q:6:5,'; h:=',
h:7:6,'; l:=',l:7:6);
end;
{Issledovanie zavisimosti potreblaemoi mosnosti OU ot razmerov poperechnogo
sechenia serdechnika magnitiprovoda (-20%..+50% ot dc=0.0024) dla MDC OU
F=const,temperatura nagreva OU T=Tdop}
readln; clrscr;
writeln('zawisimost Pp ot dc=(-20%..+50%)dc dla F=const T=Tdop');writeln;
for j:=0 to 14 do
begin
m:=5;
kz:=0.5;
ha:=0.001;
hb:=0.100;
dc:=(0.8+j/20)*24*0.001;
15:
h:=ha;
l:=m*h;
Sn:=pi*((dc+0.0001)+2*h)*l;
Svn:=pi*(dc+0.0001)*l;
Q:=h*l;
Soxl:= Sn+avn*Svn;
lcp:=pi*((dc+0.0001)+h);
if (Soxl>=0.0001) and (Soxl<=0.01) then km:=2.1*(1+0.005*(Tdop-T0))/exp(1/3*ln(Soxl));
if (Soxl>0.01) and (Soxl<=0.5) then km:=3.6*(1+0.005*(Tdop-T0))/exp(1/5*ln(Soxl));
if Soxl>0.5 then goto 2;
if Soxl<0.0001 then goto 3;
y1:=sqr(Umax/Umin)*sqr(F)*pgor/n/km/t1dop/kz-Q*Soxl/lcp;
h:=(ha+hb)/2;
l:=m*h;
Sn:=pi*((dc+0.0001)+2*h)*l;
Svn:=pi*(dc+0.0001)*l;
Q:=h*l;
Soxl:= Sn+avn*Svn;
lcp:=pi*((dc+0.0001)+h);
if (Soxl>=0.0001) and (Soxl<=0.01) then km:=2.1*(1+0.005*(Tdop-T0))/exp(1/3*ln(Soxl));
if (Soxl>0.01)and(Soxl<=0.5) then km:=3.6*(1+0.005*(Tdop-T0))/exp(1/5*ln(Soxl));
if Soxl>0.5 then goto 2;
if Soxl<0.0001 then goto 3;
y2:=sqr(Umax/Umin)*sqr(F)*pgor/n/km/t1dop/kz-Q*Soxl/lcp;
if abs(y2)<e1 then goto 14 else begin
if y1*y2<0 then hb:=h else ha:=h;
if abs(hb-ha)<e2 then goto 14 else goto 15 end;
14:
dp:=sqrt(4*pgor*lcp*F/pi/Umin);
for i:=1 to 33 do
begin
if dp>D[i] then else goto 16
end;
16:
dp:=D[i];
kz:=K[i];
dci:=D1[i];
W:=4*Q*kz/pi/sqr(dp);
Rxc:=p0*(1+a*T0)*4*W*lcp/pi/sqr(dp);
Ik:=F/W;
Pp:=Ik*Unom;
if dc=0.0240 then textcolor (red) else textcolor (white);
writeln('dc:=',dc:5:4,'; Pp:=',Pp:5:3,'; h:=',h:6:5,'; Ik:=',Ik:6:4,'; W:=',W:7:2);
end;
goto 7;
2:writeln('Soxl>0.5 m*m');goto 7;
3:writeln('Soxl<0.0001 m*m'); goto 7;
7:readln;
end.
Решение уравнения (9) дает минимально допустимый размер ОУ исходя из допустимой температуры нагрева, т.к в выражении (3) или (4) при вычислении k
т
(h
) вместо Q берется допустимая температура нагрева Qдоп
для обмоточного провода.
Для решения уравнения (9) надо задаться либо начальным приближением толщины ОУ h
0
или же допустимым интервалом изменения h
=0..h
max
. В первом случае уравнение решается методом Ньютона или итераций. Во-втором случае можно решать методом половинного деления или хорд.
Алгоритм расчета минимальной толщины ОУ методом половинного деления представлен на рис. 3.
Результаты расчета программы:
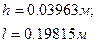
Расчет и выбор провода, а также числа витков и сопротивления ОУ в холодном состоянии осуществляется по алгоритму, изображенному на рис. 4.
Результаты расчета программы:
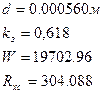
Расчет температуры нагрева ОУ. Расчет параметров ОУ в горячем состоянии
Решение уравнения (15) дает искомое значение температуры нагрева ОУ Q. При этом уравнение может решаться любым из известных методов, например, итерационным. Из (15) легко получается итерационная формула для уточнения корня уравнения:
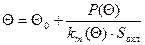 , (16) , (16)
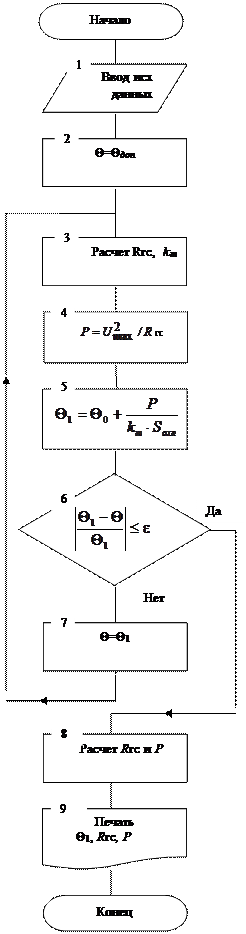
Алгоритм расчета температуры ОУ методом итераций, а также параметров ОУ в горячем состоянии, представлен на рис.5.
Результаты расчета программы:
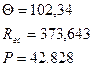
Результаты расчета сведены в таблицу 1.
Таблица 1. Потребляемая мощность обмотки управления 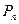
| 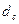
|
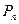
|
| 0,0192
|
26,855
|
| 0,0204
|
26,847
|
| 0,0216
|
26,831
|
| 0,0228
|
26,814
|
| 0,024
|
26,798
|
| 0,0252
|
26,774
|
| 0,0264
|
26,757
|
| 0,0276
|
26,741
|
| 0,0288
|
26,725
|
| 0,03
|
33,414
|
| 0,0312
|
33,383
|
| 0,0324
|
33,363
|
| 0,0336
|
33,323
|
| 0,0348
|
33,302
|
| 0,036
|
33,272
|
График зависимости потребляемой мощности обмотки управления от размеров поперечного сечения сердечника магнитопровода представлен на рис.6.
При увеличении диаметра сердечника 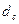 уменьшается число витков обмотки управления уменьшается число витков обмотки управления 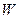 (формула (10)), а следовательно, увеличивается протекающий по обмотке управления ток (формула (10)), а следовательно, увеличивается протекающий по обмотке управления ток 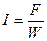 ,поэтому увеличивается мощность, потребляемая обмоткой управления ,поэтому увеличивается мощность, потребляемая обмоткой управления 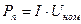 . .
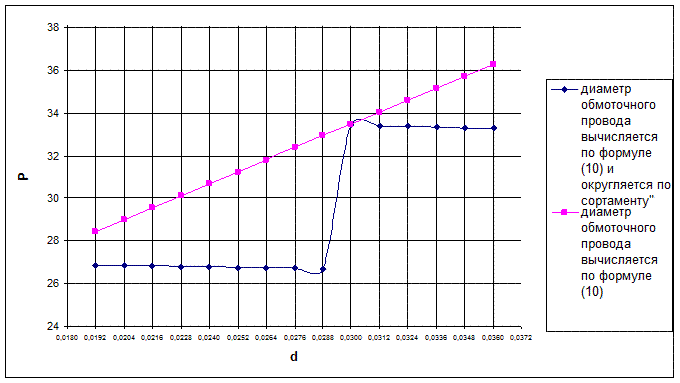
Рис. 6 - Зависимость потребляемой мощности ОУ 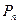 от размеров поперечного сечения сердечника магнитопровода от размеров поперечного сечения сердечника магнитопровода 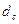
Результаты расчета сведены в таблицу 2.
Таблица 2. Потребляемая мощность 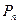 и температура нагрева ОУ и температура нагрева ОУ 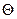
| 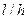
|
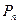
|
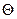
|
| 1
|
46,854
|
145,66
|
| 2
|
33,536
|
33,81
|
| 3
|
33,536
|
120,71
|
| 4
|
26,798
|
100,96
|
| 5
|
26,798
|
102,34
|
| 6
|
26,798
|
103,31
|
| 7
|
26,798
|
104,01
|
| 8
|
26,798
|
104,53
|
| 9
|
21,573
|
87,14
|
| 10
|
21,573
|
87,36
|
Графики зависимости потребляемой мощности и температуры нагрева обмотки управления от размеров поперечного сечения обмотки управления представлены на рис.7., рис.8.
С увеличением соотношения 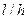 , толщина обмотки , толщина обмотки 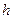 уменьшается (при условии, что уменьшается (при условии, что 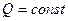 ), поэтому средняя длина витков обмотки управления ), поэтому средняя длина витков обмотки управления 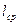 уменьшается (формула (8)) и диаметр обмоточного провода обмотки управления уменьшается (формула (8)) и диаметр обмоточного провода обмотки управления 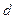 также уменьшается (формула (10)), увеличивается число витков обмотки управления также уменьшается (формула (10)), увеличивается число витков обмотки управления 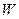 (формула (10)), а следовательно, уменьшается протекающий по обмотке управления ток (формула (10)), а следовательно, уменьшается протекающий по обмотке управления ток 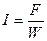 ,в результате чего уменьшается мощность, потребляемая обмоткой управления ,в результате чего уменьшается мощность, потребляемая обмоткой управления 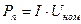 , сопротивление обмотки управления , сопротивление обмотки управления 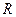 увеличивается, а мощность тепловых потерь увеличивается, а мощность тепловых потерь 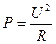 уменьшается, следовательно, температура нагрева обмотки управления уменьшается, следовательно, температура нагрева обмотки управления 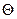 уменьшается.
уменьшается.
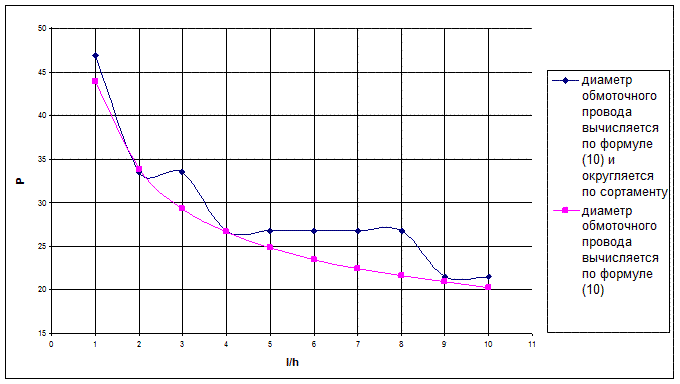
Рис. 7 - Зависимость потребляемой мощности  от размеров поперечного сечения обмотки управления от размеров поперечного сечения обмотки управления 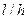
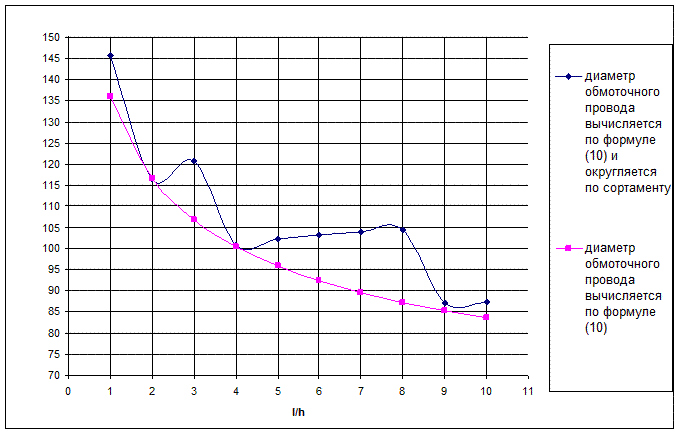
Рис. 8 - Зависимость температуры нагрева ОУ 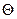 от размеров поперечного сечения обмотки управления от размеров поперечного сечения обмотки управления 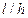 . .
Заключение
В работе приведен программный комплекс расчета обмотки управления электромагнита постоянного тока, в результате которого получены обмоточные данные и габариты обмотки управления, которые при заданном напряжении обеспечивают необходимую магнитодвижущую силу. Исследованы зависимости потребляемой мощности и температуры нагрева обмотки управления от ее размеров.
1. Никитенко А.Г., Левченко И.И., Гринченков В.П. и др. Информатика и компьютерное моделирование в электроаппаратостроении: Учеб. пособие для вузов по спец. «Электрические и электронные аппараты»/А.Г. Никитенко, И.И. Левченко, В.П. Гринченков и др.- М. : Высш. шк., 1999. - 375с.
2. Электрические и электронные аппараты: Учеб. для вузов / Под ред. Ю.К. Розанова. -2-е изд., испр. и доп. -М: Информэлектро, 2001. -420 с.: ил.
3. Основы теории электрических аппаратов. Учеб. пособие для вузов /И.С. Таев, Б.К. Буль, А.Г. Годжелло и др. Под ред. И.С. Таева. М.: Высш. шк., 1987.-352c.
4. Сахаров П.В. Проектирование электрических аппаратов. (Общие вопросы проектирования): Учеб. пособие для студентов электротехнических специальностей/ П.В.Сахаров. - М. : Энергия, 1971.-560c.
5. Руссова Н.В., Софронов Ю.В. К расчету геометрических размеров обмотки электромагнитных аппаратов постоянного тока //Тр. Академии электротехнических наук ЧР.-2003. № 4.-С. 62-66.
6. Николаев Н.Н., Свинцов Г.П. Расчет электромагнитов переменного тока и герконовых реле на ЭВМ: Метод. указ. к курсовым, дипломным проектам и работам. – Чебоксары: Чуваш. ун-т., 1989.-40c.
7. Основы теории электрических аппаратов /Под ред. Г.В. Буткевича.- М.: Высшая школа, 1970.
8. Сливинская А.Г. Электромагниты и постоянные магниты./ А.Г. Сливинская. - М.: Энергия, 1972.-248c.
|



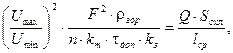 (2)
(2)

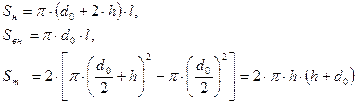
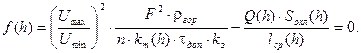 (9)
(9)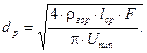 (10)
(10)