Контрольная работа: Передаточные функции одноконтурной системы

Практическая работа № 1

1. По заданным дифференциальным уравнениям определить операторные уравнения при нулевых начальных условиях, передаточные функции, структурные схемы звеньев, характеристические уравнения и их корни. Показать распределение корней на комплексной плоскости.

Оценить устойчивость каждого из звеньев.

а) ; б).

2. По заданной передаточной функции записать дифференциальное уравнение:

.

1. а). Дифференциальное уравнение можно записать в виде:

.

Обозначим Y(s) и F(s) как изображения сигналов соответственно y и f , тогда операторное уравнение (при нулевых начальных условиях) примет вид:

1,25s3Y(s) – 4s2Y(s) + 5sY(s) = 3F(s) – sF(s).

Данное уравнение можно преобразовать, вынеся Y(s) и F(s) за скобки:

Y(s). (1,25s3 – 4s2 + 5s) = F(s). (3 – s).

Отсюда получено:

.

Очевидно, что входной сигнал x отсутствует, и выходной сигнал у определяется только внешним воздействием f (система, действующая по возмущению): , то получается уравнение Y(s) = WF(s).F(s). Структурная схема объекта приведена на рис. 1.

Рис.1

Рис. 2

Передаточная функция имеет знаменатель, называемый характеристическим выражением:

A(s) =.

Если приравнять данное выражение к нулю, то образуется характеристическое уравнение , корни которого:

, и .

Распределение корней на комплексной плоскости показано на рис. 2. По рисунку видно, что корни лежат в правой полуплоскости, следовательно, объект неустойчив.

б) Дифференциальное уравнение можно записать в виде:

.

Обозначим Y(s), X(s) и F(s) как изображения сигналов соответственно y , x и f , тогда операторное уравнение (при нулевых начальных условиях) примет вид:

2s2Y(s) + 4sY(s) + 10Y(s) = 3X(s) + 4sF(s).

Данное уравнение можно преобразовать, вынеся Y(s) и X(s) за скобки:

Y(s). (5s2 + 4s + 10) = 3X(s) + 4sF(s).

Отсюда получено:

.

Если обозначить передаточные функции объекта как

и ,

то получается уравнение Y(s) = Wx(s).X(s) + WF(s).F(s). Структурная схема объекта приведена на рис. 3.

Рис. 3

Характеристическая функция имеет вид:

,

а характеристическое уравнение:

.

Корни этого уравнения равны:

и .

Распределение корней на комплексной плоскости показано на рис. 4:

Рис. 4.

Все корни характеристического уравнения лежат в левой полуплоскости, очевидно, что объект устойчив.

2. Дана передаточная функция вида:

Зная, что по определению, , получим:

, тогда:

.

Раскрывая скобки:

Применяя к полученному выражению обратное преобразование Лапласа, находим искомое дифференциальное уравнение:

.

Практическая работа № 2

Дана одноконтурная АСР, для которой определена передаточная функция регулятора (Р) с настройками и дифференциальное уравнение объекта управления (ОУ). Требуется определить:

- передаточную функцию разомкнутой системы W∞(s),

- характеристическое выражение замкнутой системы (ХВЗС),

- передаточные функции замкнутой системы Фз(s) – по заданию, Фв(s) – по возмущению, ФЕ(s) – по ошибке,

- коэффициенты усиления АСР,

- устойчивость системы.

Р - ПИ-регулятор с ПФ вида ;

дифференциальное уравнение объекта управления:

.

Определим передаточную функцию объекта:

W об( s ) .

Передаточная функция разомкнутой системы имеет вид:

Характеристическое выражение замкнутой системы:

;

Передаточные функции замкнутой системы:

- по заданию;

- по ошибке;

- по возмущению.

По передаточным функциям определим коэффициенты усиления путем подстановки в них s = 0:

К3 = Ф3(0) = 1 – по заданию;

КЕ = ФЕ(0) = 0 – по ошибке;

Кв = Фв(0) = 0 – по возмущению.

Определим устойчивость АСР по критерию Гурвица.

Так как коэффициенты ХВЗС а3 = 4, а2 = 6, а1 = 18, а0 = 4 (степень полинома n = 3), то матрица Гурвица имеет вид:

Диагональные миноры матрицы равны соответственно:

Поскольку все определители положительны, то АСР является устойчивой.

Практическая работа № 3

По табличным данным построить переходную кривую объекта, определить параметры передаточной функции объекта, рассчитать настройки ПИД-регулятора, обеспечивающие 20%-е перерегулирование.

DXвх = 5,5 кПа; DY = 0,149 %; tзап = 40 сек

Полученная переходная характеристика изображена на рисунке 5:

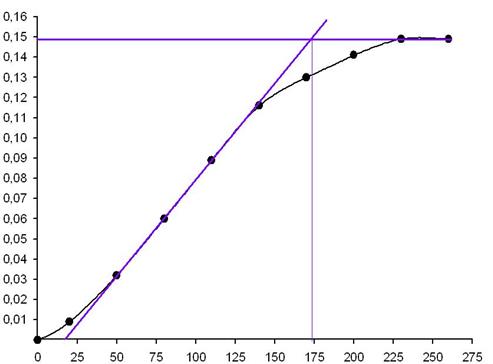
Рис. 5. Переходная характеристика.

Установившееся значение выходной величины составляет:

;

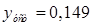Коэффициент усиления равен:

;

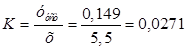Постоянная времени равна:

.

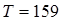Для процесса с 20 % перерегулированием ПИД-регулятора, его настройки:

;

;

.

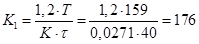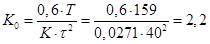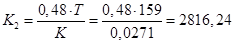Практическая работа № 4

Дана одноконтурная АСР. Требуется определить:

· передаточные функции регулятора и объекта управления,

· передаточную функцию разомкнутой системы W∞(s),

· характеристическое выражение замкнутой системы (ХВЗС),

· передаточные функции замкнутой системы Фз(s) – по заданию,

Фв(s) – по возмущению, ФЕ(s) – по ошибке,

· коэффициенты усиления АСР,

· примерный вид переходных процессов по заданию, ошибке и возмущению,

· устойчивость системы.

Структурная схема АСР:

W1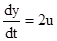(s): ; W2(s): ;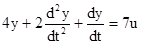

K1 = 1,2; K0 = 1,0; K = 1,0

· Передаточная функция регулятора:

.

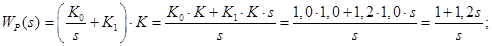· Передаточная функция объекта управления:

.

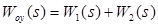Определим операторные уравнения звеньев объекта управления: для этого обозначим Y(s) и U(s) как изображения сигналов соответственно y и u , тогда операторные уравнения примут вид:

W1(s): sY(s) = 2U(s);

W2(s): 2s2Y(s)+sY(s)+4Y(s)=7U(s).

Данные уравнения можно преобразовать, вынеся Y(s) и U(s) за скобки:

W1(s): sY(s) = 2U(s);

W2(s): Y(s)·(2s2+s+4)=7U(s).

Отсюда получено:

W1(s): Y ( s ) =

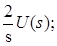
W2(s): Y(s) =.

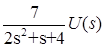Тогда:

.

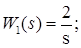
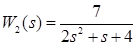Передаточная функция объекта управления:

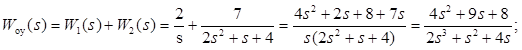
· Передаточная функция разомкнутой системы:

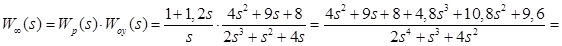
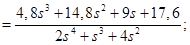
· Характеристическое выражение замкнутой системы:

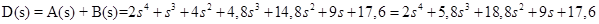
· передаточные функции замкнутой системы

Ф3(s) – по заданию:

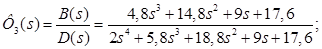
ФЕ(s) – по ошибке:

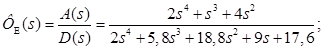
ФВ(s) – по возмущению:

При определении передаточной функции по возмущению принимается Wу.в. = Wоу. Тогда:

.

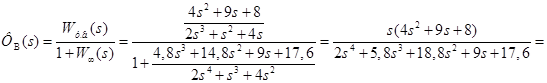
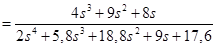· По передаточным функциям определим коэффициенты усиления путем подстановки в них s = 0:

К3 = Ф3(0) = 1 – по заданию;

КЕ = ФЕ(0) = 0 – по ошибке;

Кв = Фв(0) = 0 – по возмущению.

· Определим устойчивость АСР по критерию Гурвица.

Так как коэффициенты ХВЗС 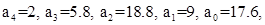(степень полинома n = 4), то матрица Гурвица имеет вид:

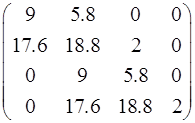
Диагональные миноры матрицы равны соответственно:

Поскольку все определители положительны, то АСР является устойчивой.

· Определим вид переходных процессов по заданию, ошибке и возмущению:

а) По заданию:

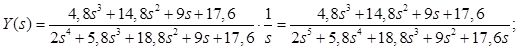
Корни знаменателя:

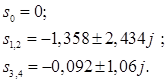
Изображение разбивается на сумму дробей:

.

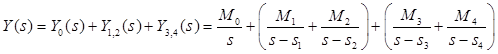Тогда оригинал y (t), согласно таблицам, имеет вид:

y (t) = y 0 + y 1,2(t) + y 3,4(t) =

+;

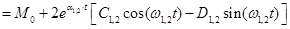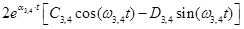где a1,2, α3,4 и w1,2, w3,4 - действительная и мнимая части пары комплексных корней s1,2 и s3,4 соответственно.

C1,2, С3,4 и D1,2, D3,4 – действительная и мнимая части пары коэффициентов М1 и М3 соответственно.

Для корня s0 = 0:

;

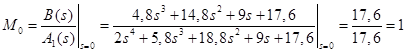Для корней :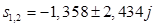

=;

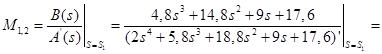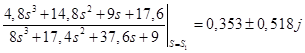Для корней :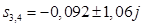

;

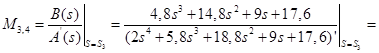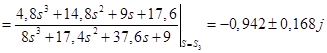Тогда:

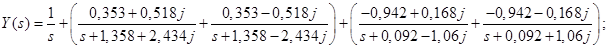
Получим оригинал:

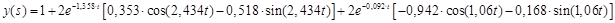
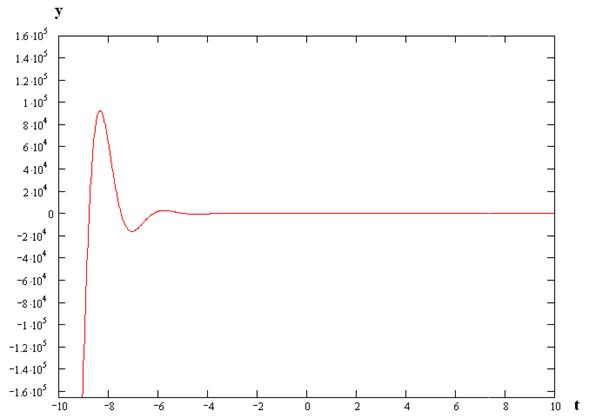
б) По ошибке:

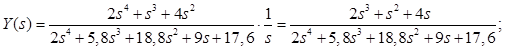
Корни знаменателя:

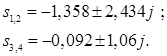
Изображение разбивается на сумму дробей:

.

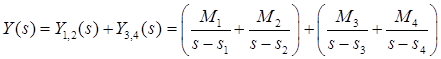Тогда оригинал y (t), согласно таблицам, имеет вид:

y (t) = y 1,2(t) + y 3,4(t) =

+;

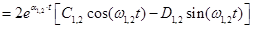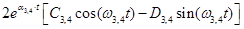где a1,2, α3,4 и w1,2, w3,4 - действительная и мнимая части пары комплексных корней s1,2 и s3,4 соответственно.

C1,2, С3,4 и D1,2, D3,4 – действительная и мнимая части пары коэффициентов М1 и М3 соответственно.

Для корней :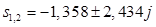

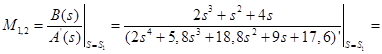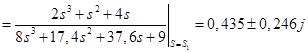
Для корней :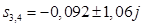

;

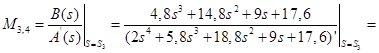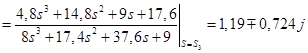Тогда:

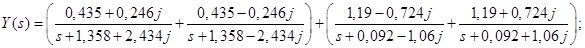
Получим оригинал:

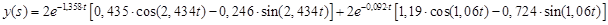
в) По возмущению:

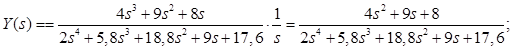
Корни знаменателя:

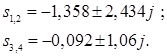
Изображение разбивается на сумму дробей:

.

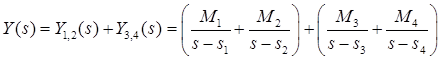Тогда оригинал y (t), согласно таблицам, имеет вид:

y (t) = y 1,2(t) + y 3,4(t) =

+;

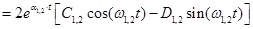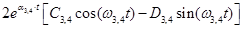где a1,2, α3,4 и w1,2, w3,4 - действительная и мнимая части пары комплексных корней s1,2 и s3,4 соответственно.

C1,2, С3,4 и D1,2, D3,4 – действительная и мнимая части пары коэффициентов М1 и М3 соответственно.

Для корней :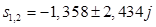

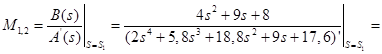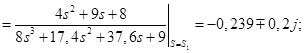
Для корней :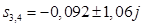

;

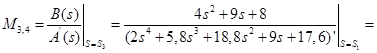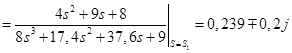Тогда:

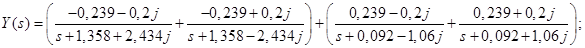
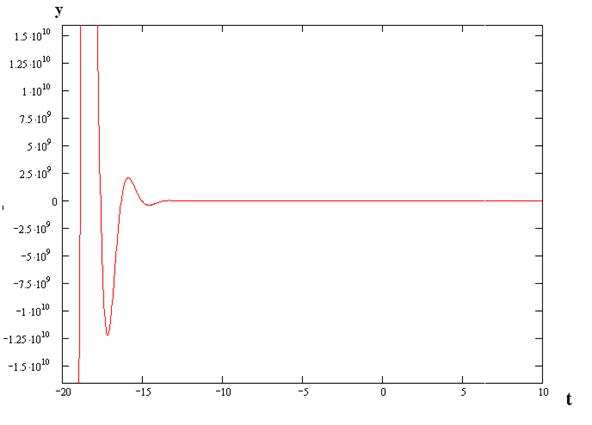
Получим оригинал:
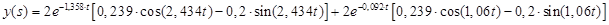
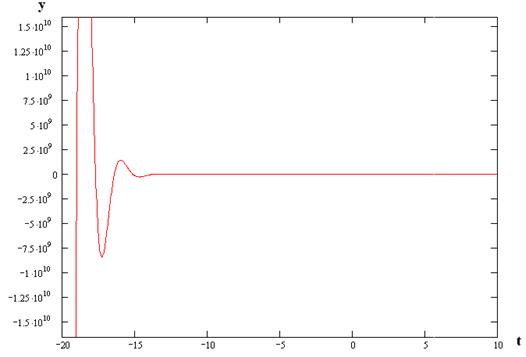