|
Лекция 1. ОБЩИЕ ПОНЯТИЯ. МОДЕЛИРОВАНИЕ
И
СХЕМАТИЗАЦИЯ
ОБЪЕКТОВ И
СВОЙСТВ
МАТЕРИАЛОВ
Созданием основ для расчёта на прочность деталей конструкций занимается наука, называемая сопротивлением материалов.
Сопротивление материалов опирается на законы и теоремы теоретической механики, но имеет и свои собственные задачи, отличные от задач механики. Для решения этих задач в сопротивлении материалов введены новые понятия.
Важнейшие и основные из них — это понятия о деформации
и об интенсивности внутренних упругих сил, или, иначе, напряжении.
Деформирование твёрдых тел
под действием внешних сил является одним из их основных свойств. Кроме того, твёрдые тела обладают способностью противодействовать изменению относительного расположения своих частиц. Это проявляется в возникновении внутри тела сил, которые не только препятствуют его деформации, но и стремятся вернуть частицы в положение, которое они занимали до деформации. Силы эти называются внутренними силами или силами упругости
. Само же свойство твёрдых тел устранять деформацию, вызванную внешними силами, после прекращения их действия называется упругостью.
Вполне упругими или абсолютно упругими
называются тела, которые после прекращения действия внешних сил полностью уничтожают вызванную ими деформацию. Совершенно неупругими
называются тела, которые и после прекращения действия внешних сил полностью сохраняют вызванную в них деформацию.
Деформация, полностью исчезающая после прекращения действия внешних сил, называется упругой деформацией
.
Неисчезающая деформация называется остаточной или пластической деформацией.
При проектировании частям конструкций придают, как правило, такие геометрические размеры, при которых в них не возникали бы остаточные деформации.
Теперь, познакомившись с понятиями о деформации и внутренних силах упругости, мы можем сказать точнее, чем занимается сопротивление материалов. А именно, в сопротивлении материалов устанавливаются для различных случаев действия внешних сил математические соотношения между внешними силами, геометрическими размерами деталей конструкций, возникающими силами упругости и деформациями.
Пользуясь этими соотношениями и характеристиками прочности материалов, определяют необходимые размеры проектируемых деталей конструкций. При установлении этих соотношений делаются некоторые допущения и ограничения. Эти допущения и ограничения
необходимы потому, что нельзя охватить сразу всю сложность изучаемых явлений.
Реклама

1. Материал, из которого изготовляются конструкции, считается непрерывным, однородным во всех точках тела и обладающим во всех направлениях одинаковыми свойствами (изотропным).
2. В сопротивлении материалов, как правило, рассматриваются только те задачи, когда деформация тел, вызванная действием внешних нагрузок, мала по сравнению с размерами тела. Это позволяет пренебречь изменениями, происходящими вследствие деформаций, в расположении действующих на тело сил.
Кроме перечисленных допущений, в сопротивлении материалов делаются и другие допущения, о которых будем говорить в соответствующих местах курса.
Схематизация
формы
физических
объектов
В ряде случаев форма конкретного элемента конструкции либо детали может быть сложной. Ее упрощение путем принятия модели формы дает возможность проведения прочностного анализа.
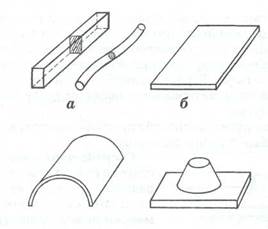
Наиболее часто в качестве моделей формы используют брусья, стержни, балки, валы, пластины, оболочки, тела.
Брус
— это твердое тело, у которого один размер (длина) значительно больше двух других (толщины и ширины) (рис.1,а). Брусья могут иметь постоянное или переменное сечение, прямолинейную или криволинейную ось (колонны, балки перекрытий, оси и валы машин и механизмов и т.п.).
Стержнем
называется брус, который нагружается силами растяжения либо сжатия. Совокупность стержней, соединенных шарнирами образует ферменную конструкцию.
Балкой
называется брус, нагруженный в основном изгибающими нагрузками. Совокупность балок, жестко соединенных между собой называется рамой.
Под валом
обычно понимается брус круглого поперечного сечения, испытывающий скручивающие и изгибающие нагрузки.
в г
Рис. 1 - Схемы изучаемых объектов: а — брусья прямые и кривые, б — пластина, в — оболочка, г – массивное тело
Пластина
— тело, образованное двумя плоскостями, где толщина существенно меньше других размеров. Примеры пластин: плоские днища, крышки баков, перекрытия различного вида. Пластина — частный случай оболочки (рис. 1,6).
Оболочка
— это конструкция, у которой один размер (толщина) значительно меньше двух других (рис. l,в). К оболочкам можно отнести корпуса ракет, самолетов, котлы, тонкостенные резервуары, топливные баки и т.п.
Реклама

Тело
— это объект (или массив), у которого все три характерных размера соизмеримы. На рис. 1, г приведен пример массивного тела (бетонная опора моста).
Схематизация
внешних
нагрузок
В сопротивлении материалов при моделировании нагружения внешние нагрузки считаются известными или заданными. Нагрузки определяют либо экспериментально, либо рассчитывают.
По характеру действия нагрузки условно разделяют на статические и динамические.
Статические нагрузки
прикладываются к исследуемому объекту медленно настолько, что вызванными ими ускорениями частиц можно пренебречь.
Динамические нагрузки
прикладываются настолько быстро, что частицы тела исследуемой конструкции получают ускорения, которыми при прочностном расчете пренебречь нельзя. Анализируемая конструкция при этом начинает двигаться (например, колебаться). К разновидностям динамических нагрузок в сопротивлении материалов относят ударные, повторнопеременные и другие.
Внешние нагрузки
по способу приложения подразделяют на сосредоточенные и распределенные.
Сосредоточенная сила
действует на части поверхности тела, размеры которых существенно малы по сравнению с общими размерами конструкции (рис. 2,а). Сосредоточенный момент или момент пары сил является силовым фактором при идеализации конструктивных особенностей изучаемого объекта. В конструкциях его обычно обозначают дугой со стрелкой (рис. 2,6).
Распределенные нагрузки
подразделяются на линейные, поверхностные и объемные. На рис. 2,в приведен пример линейно распределенной нагрузки.
Линейно распределенные
на
грузки
характеризуются интенсивностью q, т.е. нагрузкой, приходящейся на единицу длины (так называемая погонная нагрузка). Интенсивность нагрузки при ее моделировании может приниматься постоянной, линейной или изменяющейся по какому-то закону на данном участке нагружения конструкции.
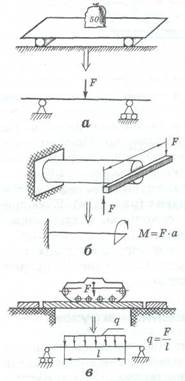
Рис.2 – Моделирование вида и способа приложения нагрузок:
а-сосредоточенная нагрузка; б-сосредоточенный крутящий момент; в-линейно распределенная нагрузка
Поверхностно распределенные нагрузки распределены по какой-либо зоне поверхности пластины, оболочки, тела.
Объемно распределенные нагрузки распределены по объему изучаемого тела. Они характеризуются интенсивностью нагрузки, приходящейся на единицу объема тела. Примерами объемной нагрузки являются массовые силы: сила тяжести, сила инерции.
Действующие на анализируемую конструкцию силы подразделяются также на активные и реактивные (или реакции связей).
Лекция 2. ВНУТРЕННИЕ
УСИЛИЯ
.
НАПРЯЖЕНИЯ
И
ДЕФОРМАЦИИ
1. Основные виды деформаций.
Внешние силы действуют на элементы сооружений и машин самым различным способом. Поэтому деформации элементов сооружений и машин, вызванные внешними силами, могут быть очень сложными. Однако эти сложные деформации всегда можно представить состоящими из небольшого числа основных видов деформаций (рис. 1- 7).
| 
Рис. 1.
|

Рис. 2.
|
 Рис.3. Рис.3.
|
| 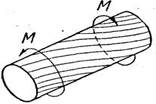
Рис. 4.
|
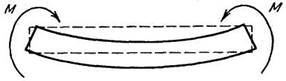
Рис. 5.
|
| 
Рис. 6.
|
Рис.7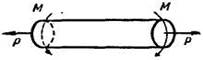
|
Эти основные виды деформаций
, изучаемые в сопротивлении материалов, следующие: 1) растяжение
(рис. 1); 2) сжатие
(рис. 2); 3) сдвиг
(срез) (рис. 3); 4) кручение
(рис. 4); 5) изгиб
(рис. 5). Примерами сложных деформаций могут служить одновременное растяжение и кручение (рис. 6) или одновременное растяжение и изгиб (рис. 7).
Метод
сечений
Проведение расчетов на прочность в сопротивлении материалов связано с необходимостью установления зависимостей между внешними силами, действующими на элементы конструкций, и возникающими при этом внутренними усилиями в материале.
Внутренние усилия, препятствующие деформации конструкции при нагружении, определяются методом сечений. Внутренние силы ищутся около некоторой точки, их связывают с определенной площадкой, проведенной через данную точку (для последующей оценки прочности именно в выбранной точке). Суть метода сечений заключается в следующем:
1. Мысленно разрезаем
исследуемую конструкцию (стержень, брус, пластину, оболочку, тело) плоскостью, проходящей через выбранную точку D на две части 1 и 2 (рис. 2.1 о).
2. Так же мысленно отбрасываем
одну из частей «разрезанного» тела, оставляя для исследования другую. Обычно для дальнейшего анализа берется та часть, к которой приложено меньше сил (на рис. 2.16 оставлена часть 1). Все тело и обе его части до «разрезания» были в равновесии, т. е. часть 1 действовала на часть 2 с такой же силой, как и часть 2 на часть 1.
3. Для того, чтобы часть 1 оставалась в равновесии после «разрезания», заменяют
действие отброшенной части 2 на нее внутренними усилиями (рис. 2.16), закон распределения которых по сечению пока неизвестен. Отметим, что часть 1 действует на часть 2 с такими же, но противоположно направленными усилиями.
4. Уравновешиваем
часть 1 — действие неизвестных внутренних усилий считаем эквивалентными их главному вектору R и главному моменту М (на рис. 2.1 в последний отмечен двумя стрелками), главный вектор и главный момент обычно приводятся к центру тяжести сечения — т. С.
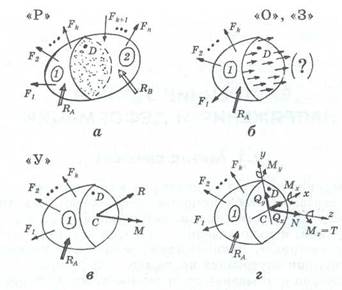
Рис. 8 - Исследуемый элемент конструкции под действием в целом уравновешенной системы как внешних сил F1
; F ...Fk
,Fn
=1
, ...Fn
, так и реакций связи RA
; RБ
мысленно «разрезанный» — а; оставшаяся часть конструкции под действием внешних сил и реакций связи, а также внутренних неизвестных усилий — б; уравновешивание оставшейся части конструкции — в; разложение главного вектора и главного момента внутренних усилий — г
По первым буквам вышеизложенной последовательности действий (разрезаем, отбрасываем, заменяем, уравновешиваем) этот метод имеет также название — метод РОЗУ
.
Описанный метод сечений (или метод РОЗУ) позволяет определить не сами внутренние усилия, а их интегральные характеристики — главный вектор R и главный момент М.
Разложение этих интегральных характеристик по осям системы координат, связанной с сечением (оси х и у лежат в сечении, ось z направлена нормально к сечению) дает шесть силовых факторов R (N, Qx
, Qy
), М (Мх
, Му
, Мz
= Т):
N — продольная (или нормальная) сила, стремящаяся либо оторвать часть1 от части 2, либо сжать их;
Qx, Qy — перерезывающие (поперечные) силы, стремящиеся сдвинуть часть 1 относительно части 2 по сечению;
Мz
= Т — крутящийся момент, пытающийся скрутить часть 1 относительно части 2 по оси z (на рис. 8,г проекции вектора момента Т показаны дугами со стрелками);
Мх
, Му
— изгибающие моменты, стремящиеся изогнуть одну часть сечения от другой относительно осей х и у соответственно.
Лекция 3. РАСТЯЖЕНИЕ И СЖАТИЕ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
Растяжением
или сжатием
называется такой вид деформации стержня, при котором в поперечном сечении возникает только продольная сила (нормальная растягивающая или сжимающая сила, не равная нулю), а все остальные внутренние силовые факторы равны нулю. В стержне при этом рассматривается поперечное, т. е. перпендикулярное оси стержня сечение.
Возьмём призматический брус (рис. 1) с постоянной площадью поперечного сечения А см2
. Нанесём на его поверхности острой иглой две неглубокие чёрточки на расстоянии l мм друг от друга. Теперь приложим по концам бруса две равные и противоположно направленные силы P так, чтобы эти силы строго действовали вдоль оси бруса. Брус, находясь в равновесии под действием растягивающих сил, удлинится в продольном направлении, а поперечные его размеры несколько уменьшатся.
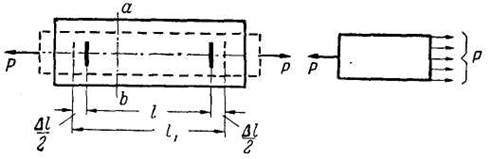
Рис. 1
При этом мы будем предполагать, что в рассматриваемом брусе все плоские сечения, нормальные к оси бруса, остаются и после деформации плоскими и нормальными к его оси. Эта гипотеза носит название гипотезы плоских сечений
. Она подтверждается опытными данными для сечений, не близких к месту приложения силы Р; принимая эту гипотезу, тем самым предполагают, что все продольные элементы бруса растягиваются совершенно одинаково.
 Принцип Сен-Венана
. Нормальное напряжение в сечении бруса распределяется равномерно в тех случаях, когда сечение значительно удалено от точки приложения сил, и неравномерно в сечениях, расположенных вблизи точки приложения силы (рис. 2). Принцип Сен-Венана
. Нормальное напряжение в сечении бруса распределяется равномерно в тех случаях, когда сечение значительно удалено от точки приложения сил, и неравномерно в сечениях, расположенных вблизи точки приложения силы (рис. 2).
Гипотеза плоских сечений устанавливает, что при растяжении (сжатии) сечение бруса остается плоским и перпендикулярным линии действия силы. Тщательно измерив расстояние между двумя нанесёнными чёрточками, мы найдём, что оно увеличилось и стало равным l1
мм. Обозначим полученное удлинение бруса через Δl; его величина будет:
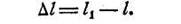
Рис. 2
Это приращение длины бруса называется полным или абсо
лютным удлинением
при растяжении; в случае сжатия бруса оно называется полным или абсолютным укорочением.
Абсолютное удлинение
, очевидно, зависит от первоначальной длины бруса. Поэтому более удобной мерой деформации является удлинение (укорочение), отнесённое к единице первоначальной длины бруса. Отношение называется относительной продольной деформацией или относительным удлинением
).
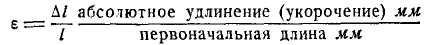
Следовательно, относительной продольной деформацией называется отношение абсолютного удлинения (укорочения) к первоначальной длине бруса. Относительное удлинение (укорочение) не имеет размерности, число это отвлечённое и часто выражается в процентах от первоначальной длины:
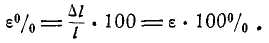
Для определения напряжения в любом поперечном сечении, т. е. в сечении, перпендикулярном к оси бруса, применим общий способ, принятый в сопротивлении материалов,— метод сечений.
Рассечём мысленно брус на две части поперечным сечением ab и правую часть отбросим. Для равновесия оставшейся левой части приложим в плоскости сечения внутренние силы упругости, направленные нормально к плоскости сечения. Силы эти заменяют действие удалённой правой части на левую часть бруса. Равнодействующая сила упругости будет действовать по оси бруса и по величине будет равна Р кг. Приняв гипотезу плоских сечений, мы тем самым приняли, что при растяжении силы упругости распределены равномерно по всему сечению, поэтому напряжение во всех точках поперечного сечения будет определяться по формуле
s=P/А, МПа
Напряжение это будет нормальным, так как оно направлено, как и сила Р, перпендикулярно к плоскости поперечного сечения. В случае сжатия бруса напряжение вычисляется по той же формуле, так как здесь изменяется только направление сил.
Нагрузки и деформации, возникающие в брусе, тесно связаны между собой. Эта связь между нагрузкой и деформацией была сформулирована впервые Робертом Гуком в 1678 г. Согласно закону Гука
деформация пропорциональна нагрузке. Этот закон является одним из основных в теории сопротивления материалов. При растяжении или сжатии бруса закон Гука выражает прямую пропорциональность между напряжением и относительной продольной деформацией:
Закон Гука при растяжении устанавливает, что нормальное напряжение, возникающее в поперечных сечениях при растяжении в пределах упругости, прямо пропорционально продольной деформации ε=ΔL/L:
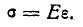
где Е — коэффициент пропорциональности, который называется модулем упругости первого рода или модулем Юнга.
Пропорциональность эта нарушается, когда напряжение переходит за некоторый предел, называемый пределом пропорциональности.
Из формулы видно, что размерность модуля упругости Е такая же, как и напряжения, так как ε — величина отвлечённая, т. е. Е выражается в МПа.
Он характеризует жесткость материала, из которого изготовлен элемент конструкции. Для различных материалов его значения определены экспериментально.
Формулу, выражающую закон Гука, можно написать и в другом виде, подставляя в неё вместо s и e их выражения:
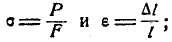
при этом получим видоизмененное выражение закона Гука:
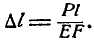
где Δl— абсолютное изменение продольных размеров; l — первоначальные размеры элемента; ЕF — величина, характеризующая жесткость сечения бруса.
Формула напряжения и закон Гука являются основными формулами при расчётах на растяжение и сжатие.
Методика
прочностного
анализа
стержневых
конструкций
Методика прочностного анализа любой конструкции содержит следующие основные разделы:
1. Определение всех внешних сил и сил реакций.
2. Построение графиков (эпюр) силовых факторов, действующих в поперечных сечениях по длине стержня (бруса).
3. Построение графиков (эпюр) напряжений вдоль оси конструкции, нахождение максимума напряжений. Проверка условий прочности в местах максимальных значений напряжений.
4. Построение графика (эпюры) деформации стержневой конструкции, нахождение максимумов деформации. Проверка в сечениях условий жесткости
Проиллюстрируем вышесказанное на примере растяжения стержня.
Пусть мы имеем прямой стержень АВ длины I постоянного сечения (например, квадратного со стороной а), жестко закрепленный на одном конце и нагруженный осевой силой F на другом (рис. 4,а). Стержень расположен горизонтально, собственным весом стержня пока пренебрегаем.
Выполним последовательно пункты методики прочностного анализа:
1. Определим величину реакции в заделке (саму заделку мысленно отбрасываем и заменяем силой реакции RAz
, (рис. 4,6). Реакцию RAz
направляем влево (если в результате получим ее величину отрицательной, значит, сила реакции направлена в противоположную сторону, т. е. вправо).
Все внешние силы и силы реакции направлены вдоль оси стержня, поэтому условие его статического равновесия в данном случае имеет вид (сумма проекций всех внешних сил и реакций связи на ось z):
-RAz
+F = O.
Получаем величину реакции RAz
= F (заключаем, что выбранное направление силы реакции верно).
2. Применим метод сечений (РОЗУ) — рассекаем стержень в произвольном сечении I - I (рис. 4, а, б) и рассматриваем равновесие либо правой части 2, либо левой части 1, т. е. отбрасываем одну из частей. Действие внутренних силовых факторов, заменяем равнодействующей силой N в сечении площадью А:
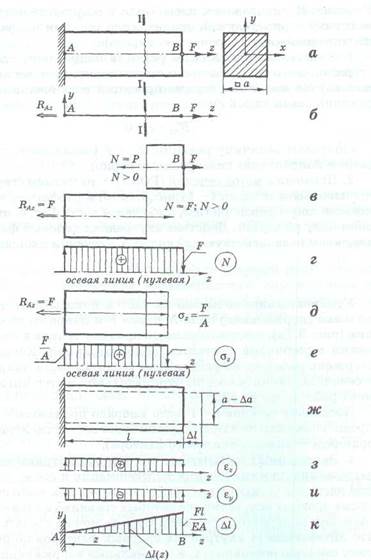
Рис. 3.1.
Исследуемый элемент конструкции — а; расчетная схема — б; метод сечений — в; эпюра продольной силы — г; распределение нормальных напряжений по поперечному сечению — д; эпюра нормальных напряжений е; схема деформации стержня — ж; эпюра продольных деформаций — з; эпюра поперечных деформаций — и; эпюра продольных удлинений — к
Уравновешивание любой из частей показывает, что продольная (нормальная) сила N равна F и направлена от сечения (рис. 4,в), следовательно, по правилу знаков в сопромате считается положительной. Поскольку сечение 1-1 было выбрано произвольно, эпюра продольной силы по длине стержня будет постоянной (рис. 4, г, ордината – значение силового фактора).
3. Эксперимент показывает, что при рассматриваемом виде нагружения плоские сечения до деформации и после приложения нагрузки остаются плоскими (кроме краевых зон, величина которых сравнима с размером поперечного сечения). Отсюда можно сделать вывод, что интенсивность внутренних силовых факторов по поперечному сечению постоянна, т.е. нормальные напряжения одинаковы в любой точке поперечного сечения и равны (рис. 4, д):
sz
= N/A=F/A
Как и эпюра продольной силы, эпюра нормальных напряжений неизменна по длине (рис. 4,е).
4. Процесс анализа деформации стержня при растяжении показывает, что весь стержень удлинится на Ñl (абсолютная деформация) и его поперечные размеры сократятся на Ñа. Поскольку поперечные сечения остаются параллельными друг другу и после нагружения, то относительная продольная деформация любого продольного отрезка при растяжении постоянна и в нашем случае равна (рис. 4, ж, з):
ez
=Ñl/l
Относительная деформация — величина безразмерная (иногда задается в %).
Гипотеза упругости (физическая связь между напряжениями и деформациями) в случае растяжения (сжатия) стержневого элемента (закон Гука при растяжении - сжатии) имеет вид:
sz
=
ez
×Е,
где Е — модуль упругости материала (первого рода) или модуль Юнга — физическая характеристика, определяемая из опыта. В данной конкретной задаче (рис. 4,з) продольная деформация постоянна вдоль оси стержня и равна
ez
=
sz
/Е = F/ЕА.
Величина ЕА – жесткость стержня на растяжение-сжатие. Эксперимент показывает, что отношение величин поперечной деформации к продольной для изотропных материалов практически постоянно и оценивается коэффициентом Пуассона (физическая характеристика материала – коэффициент поперечной деформации):
m = -ey
/ ez
Эпюра поперечной деформации представлена на рис. 4,и. Величина m для широкого класса конструкционных материалов изменяется в диапазоне
0 £ m £ 0,5
Полное удлинение стержня: при постоянном значении N и площади сечения А равно:
Ñl=Fl/EA
На рис. 4, к представлена линейная эпюра изменения текущего значения Ñl(z) в зависимости от координаты z ( в т. А жесткая заделка – перемещений нет).
Если наряду с внешними нагрузками имеется температурное воздействие, то согласно постулату о принципе независимости действия сил полная деформация есть суперпозиция силовой и температурной деформации, т.е.
ez
= sz
/Е + a×Ñt,
где a - коэффициент температурного расширения; Ñt – разность температур нагретого тела и исходного (обычно 20 0
С). В нашем случае при нагреве растягиваемого стержня полная абсолютная деформация (или удлинение) равна:
Ñl = Fl/ЕА + a×l×Ñt.
Лекция 4. ИСПЫТАНИЕ МАТЕРИАЛОВ НА РАСТЯЖЕНИЕ И СЖАТИЕ
Основные механические характеристики материалов получают в результате специальных лабораторных исследований на испытательных машинах при нагружении стержней на растяжение и сжатие. Вид стержневых образцов и сами методы испытаний регламентированы государственными стандартами.
Испытания на растяжение образцов испытуемого материала производятся на специальных разрывных машинах. Образцы обычно бывают круглого (рис.1), реже - прямоугольного, сечения. На концах образцы имеют головки в виде утолщения.
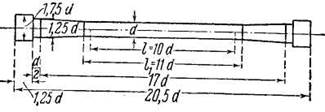
Рис. 1
Диаграмма растяжения
Рассмотрим типичную диаграмму испытаний, характерную для образцов из малоуглеродистых сталей, полученную при нормальной температуре и стандартных скоростях деформирования при нагружении (рис. 2).
Рис.2. Диаграмма испытаний, вид и характер деформации стандартных образцов
На диаграмме растяжения могут быть условно выделены четыре характерных участка для различных стадий деформирования образца:
ОА — участок упругости (пропорциональности
), на котором видна прямопропорциональная зависимость между растягивающей силой и вызываемого ею удлинения (абсолютной деформации). На этом участке абсолютная деформация достаточно мала (до 0,02 %).
АВ — участок (или площадка) текучести
, где деформации растут без заметного повышения нагрузки. Следует отметить, что у многих конструкционных металлов участок текучести отсутствует (дюралюминий, легированные стали и др.). Деформации текучести достигают 0,2 %.
ВС
— участок упрочнения
, на котором отмечается новый, но более медленный, чем на первом участке, рост нагрузки. В конце этого участка на образце начинает образовываться шейка — местное сужение образца, это намечается место будущего разрыва, а растягивающая сила F достигает максимального значения. Деформация при этом около 15% .
CD
— участок разрушения
(местной пластической деформации), на котором удлинение всего образца уже происходит за счет местной деформации в зоне шейки, площадь которой существенно уменьшается. Поэтому для разрушения требуется меньшее усилие. Отметим, что многие материалы разрушаются без заметного образования шейки.
Диаграмма деформирования
является базовой для характеристики материала в сопротивлении материалов и получается из диаграммы испытаний, когда размеры образца исключаются путем деления растягивающей силы на первоначальную площадь, а абсолютного удлинения на начальную длину образца. Строится зависимость s = ¦(e) — рис. 3, а. Неучет изменения поперечных размеров за счет эффекта Пуассона делает эту диаграмму в определенной мере условной.
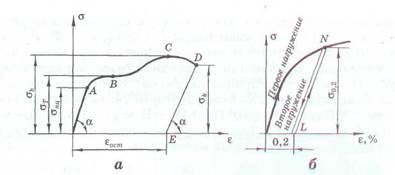
Рис. 3 - Диаграмма деформирования с участком текучести — а; без него — б
На диаграмме деформирования сохраняются те же характерные участки. Соответственно им следующие характеристики материалов имеют названия:
s
пц
— предел пропорциональности;
s
т
— предел текучести;
s
b
— предел прочности;
s
k
— напряжение в момент разрушения.
Если материал не имеет выраженной площадки текучести, то предел текучести назначается по допуску на пластические деформации. Наиболее распространенным значением предела текучести sт
является s02
, где 0,2 означает, что остаточная деформация при этом значении равна 0,2 % (рис. 3, 6).
В качестве характеристик пластичности (наряду с sт
) используются остаточное удлинение d (%) и остаточное сужение jk
(%):
d=Ñl/l0
; jk
=A0
– Ak
/Ak
,
где l0
, А0
– первоначальная длина образца и площадь; lk
, Ak
– длина и площадь после разрушения (разрушенные части образца соединяются и производятся измерения).
Чем больше параметры d и jк
, тем пластичнее материал. Тангенс угла наклона участков ОА, LN диаграмм деформирования и будет модулем упругости материала (первого рода) или модулем Юнга: Е = tga (рис. 3). Размерность модуля упругости — это размерность напряжений, т. к. относительная деформация — величина безразмерная (в ряде случаев указывается в процентах). В технике принято и напряжения, и модуль упругости указывать в мегапаскалях — МПа (1 МПа = 106
Па, 1 Па = Н/м2
, 1 МПа - 1 Н/мм2
).
Условие прочности и жесткости
при растяжении (сжатии)
Расчет на прочность по допускаемым напряжениям основан на том, что наибольшее расчетное напряжение
в опасном сечении стержневой конструкции не превосходит допускаемого (меньше — не более 10% , больше — не более 5%):
sр
£[s].
В случае растяжения (или сжатия) стержня
sр
= sz
,
sz
= N/A.
Допускаемое напряжение
– это наибольшее напряжение, при котором обеспечивается требуемая прочность, жесткость и долговечность элемента конструкции в заданных условиях его эксплуатации.
Допускаемое напряжение составляет некоторую долю от предельного напряжения sпред:
[s] = sпред
/ [n],
где [n] - нормативный коэффициент запаса, показывающее, во сколько раз допускаемое напряжение меньше предельного. В сопромате за sпред
принимают для пластичных материалов sТ
– предел текучести, а для хрупких sВ
– предел прочности.
Фактический коэффициент запаса прочности
(или рабочий коэффициент) для опасного сечения есть
n = sпред
/ sр
.
Можно проводить три вида расчетов:
1. Проверочный
– по известным размерам и материалу стержня (заданы площадь сечения А и [s]) проверить, в состоянии ли он выдержать заданную нагрузку [N]
sр
= N/A£ [s].
2. Проектный –
по известным нагрузкам (N задано) и материалу элемента - [s] ) подобрать необходимые размеры поперечного сечения, обеспечивающего его безопасную работу:
А ³ N / [s].
3. Определение допускаемой внешней нагрузки
– по известным размерам (А задано) и материалу конструкции ([s]- дано) найти допускаемую величину внешней нагрузки:
[N] £ [s] × А.
Оценка жесткости стержневой конструкции
проводится на основе проверки условия жесткости при растяжении: Ñl< [Ñl]
Величина допускаемой абсолютной деформации [Ñl] назначается отдельно для каждой конструкции.
Аналогично расчетам по условию прочности условие жест
кости
также предполагает три вида расчетов:
1) проверка жесткости данного элемента конструкции
, т. е. проверка выполнения условия ;
2) расчет проектируемого стержня,
т. е. подбор его поперечных A³N×l/(E[Ñl]);
3. установка работоспособности данного стержня
, т. е. подсчет допустимой нагрузки [N] = [l] × EA/l.
Лекция 5. Решение
статически
определимых
задач
Перед рассмотрением конкретных примеров необходимо отметить, что в задачах на растяжение (сжатие) стержней внешние силы (и реакции связей) действуют вдоль оси стержня (или их равнодействующая приложена вдоль оси стержня), т. е. имеет место одноосное нагружение, поэтому и условие равновесия конструкции как твердого тела в пространстве сводится к равенству нулю суммы проекций всех внешних сил и сил реакций на эту ось, т. е.  Fiz
= 0 Fiz
= 0
где i — общее число силовых факторов и реакций.
Известно, что для плоской системы сил можно составить три уравнения равновесия:
— сумма проекций всех сил и сил реакций на одну из координатных осей равна нулю, например:  Fiz
= 0 Fiz
= 0
— сумма проекций всех сил и сил реакций на другую ось плоскости действия сил равна нулю, пусть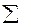 Fiy
= 0 Fiy
= 0
-сумма моментов всех внешних сил и сил реакций относительно любой точки этой плоскости равна нулю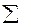 momA
(Fi
)=0 momA
(Fi
)=0
где т. А произвольна.
Иногда для плоской системы сил бывает рациональнее принять три уравнения в другом виде, но «новые» уравнения суть следствия трех вышеназванных:
— сумма проекций всех сил и сил реакций на одну из координатных осей плоскости равны нулю, например: 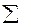 Fiz
= 0 Fiz
= 0
-сумма моментов всех внешних сил и сил реакций относительно любой точки плоскости равна нулю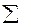 momA
(Fi
)=0 momA
(Fi
)=0
-сумма моментов всех внешних сил и сил реакций относительно другой точки плоскости равна нулю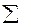 momB
(Fi
)=0 momB
(Fi
)=0
(т. А и В выбираются из соображений рациональности составления уравнений равновесия).
Типичное моделирование условий закрепления концов стержней для плоской системы сил показано на рис. 1.
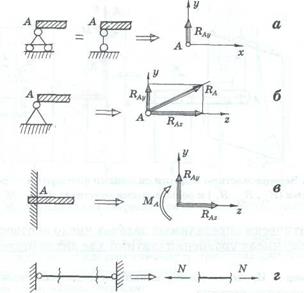
Рис. 1. Моделирование видов закрепления действием реактивных силовых факторов: шарнирно-подвижная опора — а (реакция вертикальная); шарнирно-неподвижная опора— б (направление реакции неизвестно, ищутся две ее составляющие RAy
, RAz
); жесткая заделка — в (три неизвестных силовых фактора — две силы и один момент); стержень, шарнирно закрепленный с двух концов — г (принято считать, что он работает на растяжение или сжатие)
В общем случае пространственной системы сил можно составить шесть уравнений равновесия для стержня:
— сумма проекций всех сил и сил реакций относительно одной координатной оси равна нулю, например: 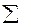 Fi
х
= 0 Fi
х
= 0
— сумма проекций всех сил и сил реакций относительно другой координатной оси равна нулю, например:  Fiy
= 0 Fiy
= 0
— сумма проекций всех сил и сил реакций относительно третьей координатной оси равна нулю, например: 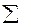 Fiz
= 0 Fiz
= 0
К ним добавляются три уравнения равенства моментов всех сил и реакций относительно этих координатных осей:
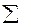 momx
(Fi
)=0 momx
(Fi
)=0
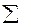 momy
(Fi
)=0 momy
(Fi
)=0
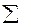 momz
(Fi
)=0 momz
(Fi
)=0
На рис. 2 представлено моделирование жесткого закрепления балки – заделка заменена шестью реактивными силовыми факторами.
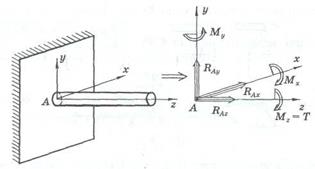
Рис. 2. Замена жесткой заделки силовыми факторами — реактивными силами (RAx
, RAy
, RAz
) и реактивными моментами (Мх
, Мy
, Мz
= Т)
В статически определимых задачах число неизвестных реакций равно числу уравнений статики для анализируемого тела.
Пример 1.
Провести оценку влияния собственного веса на продольную деформацию стержня (рис. 3).
Пусть длина стержня I, площадь поперечного сечения А, собственный вес G, модуль упругости материала стержня Е.
Решение.
1. Условие равновесия (сумма проекций всех сил на ось z) позволяет определить реакцию в заделке (сила веса G направлена вдоль оси z):
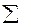 Fiz
= 0; G-RAz
=0; RAz
=G Fiz
= 0; G-RAz
=0; RAz
=G
2. Применяем метод РОЗУ и определяем продольную силу в сечении 1 -1, она равна весу оставшейся части конструкции:
G′
=G/l(l-z), N=G¢
= G/l(l-z)
3. Нормальные напряжения при этом равны:
sz
=s=N/A=G/l×A(l-z).
Максимальные нормальные напряжения, очевидно, будут в заделке при z = 0:
smax
=Gl/lA=Gl/V=gl,
где V = Al — объем стержня, g— удельный вес.
Проведем численную оценку: имеем стержень из мягкой стали длиной l = 100 м, g= 106
0,0785 Н/м3
, [s] =180 МПа. Тогда smax
= 106
0,0785 100 = 7,85 106
Н/м2
= 7,85 МПа, что составляет меньше 5% от величины [s].
Таким образом, можно сделать вывод, что влияние собственного веса стержневой конструкции следует учитывать при очень длинных стержнях (например, для канатов подъемников).
Рис. 3. Расчетная схема стержня при оценки собственного веса
4. Оценим деформацию стержня:
ez
=s/E=g(l-z)/E.
Текущее значение абсолютного удлинения ∆l(z):
∆l(z)=g/E¦0
z
(l-z)dz
Полное абсолютное удлинение стержня при z=l равно:
∆l=gl2
/2E=Gl/2EA
или удлинение стержня под действием собственного веса вдвое меньше, чем удлинение под действием такой же по величине, как вес, нагрузки, но приложенной к концу стержня .
Лекция 5. ИЗГИБ. УСТОЙЧИВОСИТЬ СЖАТЫХ СТЕРЖНЕЙ
Многие элементы конструкций (балки, рельсы, оси всех колес и т.д.) испытывают деформацию изгиба.
Возьмём прямолинейный призматический брус с продольной плоскостью симметрии (рис. 1); приложим в этой плоскости уравновешенные силы, действующие перпендикулярно к оси бруса. Брус под действием этих сил изогнётся, ось его искривится.
Рис. 1
Изгибом
называется деформация от момента внешних сил, действующих в плоскости, проходящей через геометрическую ось балки. В зависимости от места приложения действующих сил различают прямой и косой изгиб.
Изгиб называется прямым
, если внешние силы, действующие на балку, лежат в главной плоскости сечения.
Главной плоскостью сечения называется плоскость, проходящая через ось балки и одну из главных центральных осей сечения.
Изгиб называется косым
, если внешние силы не лежат в главной плоскости сечения.
В зависимости от характера внутренних силовых факторов, возникающих в поперечных сечениях балки, изгиб может быть чистым и поперечным.
Изгиб называется чистым
, если в поперечном сечении балки (бруса) возникает один изгибающий момент МИ
.
Изгиб называется поперечным
, если под действием внешних сил в сечении балки (бруса) возникают изгибающий момент МИ
и поперечная сила Qy
Для наглядного представления деформации изгиба возьмём небольшой призматический резиновый стержень. Начертим на его грани две линии, параллельные друг другу и перпендикулярные к оси стержня. Приложим по его концам в плоскости симметрии два равных, но противоположно направленных момента (рис. 2, а). Стержень под действием изгибающих моментов прогнётся, начерченные прямые останутся прямыми и перпендикулярными к изогнутой оси стержня (рис. 2, б).
Видно, что плоские сечения взаимно поворачиваются одно относительно другого. Очевидно, такой поворот происходит вследствие растяжения одних волокон материала и сжатия других. Отсюда легко сделать заключение, что у балки имеется такой слой волокон, который не испытывает ни растяжения, ни сжатия. Этот слой называется, нейтральным слоем. Линия пересечения нейтрального слоя с плоскостью какого-либо поперечного сечения называется нейтральной осью (линия nn).
Кроме того, на той же резиновой модели легко заметить что продольное укорочение волокон на вогнутой стороне сопровождается удлинением в поперечном направлении, а продольное удлинение волокон на выпуклой стороне — сужением в поперечном направлении, т. е. явления протекают так же, как при простом растяжении и сжатии. Вследствие этого верхняя и нижняя стороны сечения, т. е. линии ab и cd, искривятся, причём центр кривизны их будет один и тот же. Верхняя линия ab удлинится, а нижняя cd укоротится.
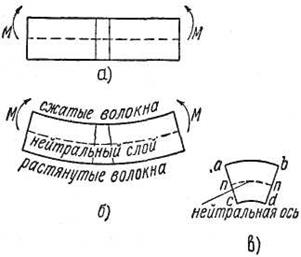
Рис. 2
Вследствие удлинения одних волокон и укорочения других, вызываемых в брусе изгибающими моментами, в поперечных сечениях бруса возникают нормальные напряжения растяжения и сжатия. Величина этих напряжений в данном поперечном сечении зависит от величины действующего в этом сечении изгибающего момента. Выше мы видели, что в случаях изгиба бруса силами, кроме изгибающего момента, в поперечных сечениях действуют ещё поперечные силы, стремящиеся произвести сдвиг бруса. Поперечные силы вызывают в брусе касательные напряжения, величина которых в сечении зависит от величины поперечной силы в данном сечении. Таким образом, в изгибаемом силами брусе возникают нормальные и касательные напряжения.
Прежде чем перейти к определению величин этих напряжений, рассмотрим способы определения изгибающих моментов и поперечных сил в различных поперечных сечениях изгибаемых брусьев.
Опоры и опорные реакции балок.
Опоры балок по их устройству могут быть разделены на следующие три основных типа:
1)шарнирно-неподвижная опора,
2)шарнирно-подвижная опора
3)жёстко-защемляющая опора.
Шарнирно-неподвижная опора показана на фиг. 3, а. Конец балки опирается на каток О. Последний лежит на опорной подушке А, которая в свою очередь жёстко прикреплена к опорной плоскости N. Такая опора не даёт концу балки возможности передвигаться в каком-либо направлении, позволяя ему только поворачиваться относительно центра шарнира О.
В дальнейшем неподвижно-шарнирную опору будем изображать схематически, как указано на фиг. 3, б. Относительно реакции, возникающей в шарнирно-неподвижной опоре, известно только, что она лежит в плоскости действия нагружающих балку сил и проходит через центр шарнира. Величина и направление реакции нам неизвестны. Неизвестную по величине и направлению реакцию R всегда можно заменить двумя составляющими её реакциями: одной вертикальной А и другой горизонтальной Н. В этом случае вместо реакции, неизвестной по величине и направлению, получим две реакции, известные по направлению и неизвестные по величине. Таким образом, можно сказать, что шарнирно-неподвижная опора даёт две неизвестные по величине реакции.
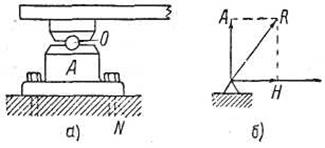
Рис. 3
Шарнирно-подвижная опора показана на фиг. 4, а. Такая опора отличается от неподвижно-шарнирной тем, что у неё опорная подушка поставлена на катки, дающие ей возможность передвигаться вместе с концом балки вдоль оси последней по опорной плоскости N. В дальнейшем шарнирно-подвижную опору будем изображать схематически, как указано на фиг. 4, б. Шарнирно-подвижная опора налагает на конец балки только одну связь — она не дает возможности перемешаться концу балки в направлении, перпендикулярном к оси балки. Следовательно, шарнирно-подвижная опора даёт лишь одну реакцию, неизвестную по величине, но известную по направлению.
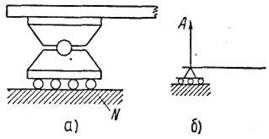
Рис. 4
Жёсткое защемление конца балки показано схематически на рис. 5. Такая опора препятствует всякому перемещению конца балки в плоскости действия внешних нагрузок и, кроме того, она препятствует вращению конца балки.
В жёстком защемлении возникает реакция, неизвестная по величине и направлению, препятствующая перемещению конца балки, и реактивный момент, препятствующий повороту конца балки. Неизвестную реакцию R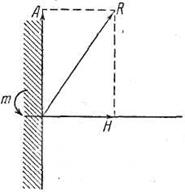 можно всегда заменить двумя реакциями: одной вертикальной А и другой горизонтальной Н. На этом основании можно сказать, что на опоре, представляющей жёсткое защемление, возникают три неизвестные реакции: вертикальная реакция А, горизонтальная реакция Н и опорный момент m. можно всегда заменить двумя реакциями: одной вертикальной А и другой горизонтальной Н. На этом основании можно сказать, что на опоре, представляющей жёсткое защемление, возникают три неизвестные реакции: вертикальная реакция А, горизонтальная реакция Н и опорный момент m.
Рис. 5
В практике чаще всего силы, изгибающие балку, действуют перпендикулярно к оси балки. В этих-случаях число неизвестных реакций, возникающих на опорах, уменьшается, так как реакция вдоль оси балки в шарнирно-неподвижной опоре и в опоре, представляющей жёсткое защемление конца, делается равной нулю. Таким образом, для балок, изгибаемых нагрузками, перпендикулярными к оси балки, будем иметь: в шарнирно-неподвижной и шарнирно-подвижной опорах по одной неизвестной реакции А, направленной перпендикулярно к оси балки, в жёстком защемлении — две неизвестные реакции: реакцию А, перпендикулярную к оси балки, и реактивный момент m.
Определение опорных реакций балок.
В случае действия на балку сил, лежащих в одной плоскости, статика дает три уравнения равновесия:
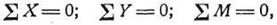
т. е. для равновесия балки необходимо, чтобы суммы проекций всех сил, приложенных к балке, вместе с реакциями опор на оси х и у были равны нулю.
Кроме того, должна быть равна нулю и сумма моментов всех сил.
Если силы, изгибающие балку, перпендикулярны к её оси, то уравнение ∑Х = 0 обращается в тождество и для определения реакций остаётся два уравнения статики:
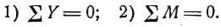
Если балка при поперечном изгибе имеет такие опоры, что общее число реакций, возникающих на опорах, не превосходит двух, то последние могут всегда быть определены из двух уравнений статики.
Такие балки, реакции которых могут быть определены из уравнений статики, называются статически определимыми балками. Статически определимые балки могут быть только следующих двух видов:
1) балка с одним жёстко-защемлённым и другим свободным концом (рис. 6, а) и
2) балка с одной шарнирно-неподвижной и другой шарнирно-подвижной опорами (рис. 6, б и 6, в).
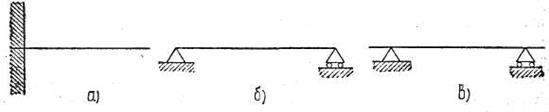
Рис. 6
Балка, изображённая на фиг. 6, в, имеет свешивающиеся концы. Такую балку принято называть консольной, а свешивающиеся концы — консолями.
Балки, у которых общее число реакций опор больше числа уравнений равновесия статики, называются статически неопределимыми. В случае статически неопределимых балок реакции опор определяются из совместного решения уравнений статики и уравнений деформации балок.
Изгибающий момент в любом сечении балки равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть балки: МИ
= ΣМ0
(Fi
).
Поперечная сила в любом сечении балки равна алгебраической сумме проекций внешних сил, действующих на отсеченную часть балки: Qy
= ΣFiy
.
Значения поперечных сил и изгибающих моментов в различных сечениях балки могут быть неодинаковы, поэтому строятся эпюры поперечных сил и изгибающих моментов. Для определения поперечных сил и изгибающих моментов необходимо знать правила знаков.
Правила знаков для поперечных сил.
-поперечная сила считается положительной в том случае, если внешние силы поднимают левый конец балки или опускают правый (рис. 7,а).
-поперечная сила считается отрицательной в том случае, если внешние силы опускают левый конец балки или поднимают правый конец (рис. 7,б).
а б
Рис. 7
Правила знаков для изгибающих моментов.
-изгибающий момент считается положительным, если внешние силы, действующие на левый конец балки, поворачивают его по часовой стрелке, а действующие на правый — против часовой стрелки (рис. 8,а).
-изгибающий момент считается отрицательным, если внешние силы, действующие на левый конец балки, поворачивают его против часовой стрелки, а действующие на правый — по часовой стрелке (рис. 8,б).
а б
Рис. 8
Последовательность построения эпюр поперечных сил
и изгибающих моментов:
1. Под нагруженной балкой строим расчетно-графическую схему.
2. Используя три уравнения: ΣFix
=0, ΣFiy
= 0, ΣM(Fi
) = 0, определяем реакции опор балки (обязательно выполнить проверку решения).
3. Используя метод сечений, определяем значения поперечных сил в характерных точках, т.е. точках, в которых приложены внешние нагрузки (при этом удобнее использовать прямое правило знаков, т.е. разбивать балку слева направо).
4. По полученным значениям поперечных сил строим эпюру Qy
под балкой проводим прямую, параллельную ее оси, и от этой прямой в характерных точках откладываем перпендикулярные поперечным силам отрезки, соответствующие выбранному масштабу.
5. Используя метод сечений, определяем величину Ми
в тех же характерных точках и по полученным значениям строим эпюру изгибающих моментов.
Характерные особенности построения эпюр
Qy
; Ми
1. На участке балки, где действуют сосредоточенные силы, эпюра Qy
очерчивается прямой, параллельной оси балки, а эпюра Ми
— наклонной прямой.
2. На участке балки, где действует распределенная нагрузка, эпюра Qy
очерчивается наклонной прямой, а эпюра Ми
— параболой выпуклостью навстречу распределенной нагрузке.
3. В точке балки, где приложена сосредоточенная сила, на эпюре Qy
наблюдается скачок на величину этой силы, а на эпюре Ми
— излом.
4. В точке балки, где приложен внешний момент, на эпюре Qy
не наблюдается никаких изменений, а на эпюре Ми
наблюдается скачок на величину внешнего момента.
При деформации изгиба возникает нормальное напряжение. Напряжения одинаковы в сечении балки по ширине, но изменяются по высоте балки.
Условие прочности при изгибе
: рабочее напряжение должно быть меньше или равно допускаемому напряжению, т.е.
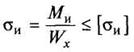
где Wx
— осевой момент сопротивления (величина, характеризующая способность элементов конструкции сопротивляться деформации изгиба).
Осевой момент сопротивления сечения определяется по формулам:
| а) для круга (рис. 9, а)
|
б) для кольца (рис. 9, 6)
|
в) для прямоугольника (рис. 9, в)
|
| 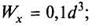
|
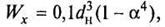
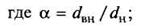
|
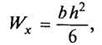
|
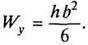
|
а б в
Рис. 9
Три расчета на прочность при изгибе.
1.
Проверочный:
| 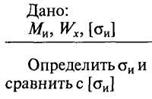
|
Решение:
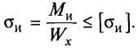
|
2.
Проектный.
| 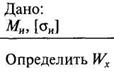
|
Решение:
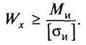
|
3. Проверочно-уточненный.
| 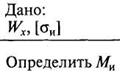
|
Решение:
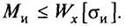
|
При прямом поперечном изгибе в поперечных сечениях бруса возникают изгибающий момент МИ
, который обусловливает возникновение нормального напряжения σи
, и поперечная сила Qy
, которая обусловливает возникновение в этом же сечении касательного напряжения τи
(рис. 10):
Рис. 10
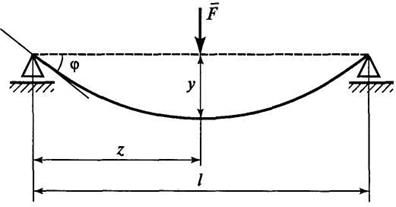
Под действием внешних сил ось бруса испытывает линейное перемещение y и угловое перемещение φ (рис. 11). Линейные и угловые перемещения определяют по формулам, которые составлены с учетом вида нагрузок, направления их к оси бруса и места приложения к брусу. Эти формулы занесены в специальные таблицы.
| 
|
Например, если z= ½ L, то
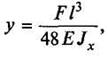
где EJX
— жесткость сечения бруса при изгибе.
|
| Рис. 11
|
|
Условие жесткости при изгибе
: рабочее линейное или угловое перемещение должно быть меньше или равно допускаемому линейному или угловому перемещению, т.е.
Лекция 7. КРУЧЕНИЕ
Деформации кручения подвергаются многие детали машин и конструкций: валы, пружины и пр. Кручением
называется такой вид деформации брусьев, при котором в любом поперечном сечении внутренние усилия приводятся только к крутящему моменту Т = Мг
(рис. 2.1, 5.1), а остальные силовые факторы равны нулю (N = Qx
= Qy
= 0; Mx
= My
= 0).
Брусья, работающие на кручение, называются валами. В машинных передачах валы, кроме кручения, испытывают обычно также изгибные нагрузки (изгиб) от натяжения цепей, ремней, взаимодействия зубчатых колес и т.п., и от веса самих валов. В проектных расчетах валы рассчитывают вначале лишь на кручение (т. е. конструкция вала создается из условия его прочности при кручении). При незначительных изгибающих моментах расчет так называемых легких валов ведется только на кручение.
Прежде чем перейти к выводу уравнений для определения напряжений и деформаций при кручении, остановимся на некоторых экспериментальных результатах.
Возьмем круглый цилиндр, нижний конец которого, закрепим в неподвижной плоскости N (рис. 1, а) а к его свободному верхнему концу приложим пару сил с моментом Мк
действующую в плоскости, перпендикулярной к оси цилиндра. Цилиндр под действием этого момента будет испытывать деформацию, называемую кручением. При кручении цилиндра его ось ОО остается прямой. Ось эта называется осью кручения. Если на боковой поверхности цилиндра до начала кручения была нанесена сетка, образованная окружностями и образующими (рис.1, б), то после деформации произойдет следующее (рис. 1, в).
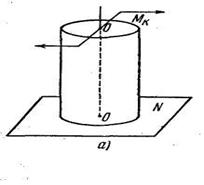 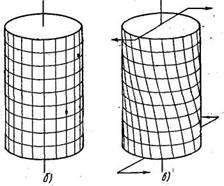
Рис. 1
1) Квадраты, образованные этой сеткой, обратятся в совершенно одинаковые ромбы.
2) Круговые сечения цилиндра останутся круглыми с прежним диаметром.
3) Расстояния между окружностями не изменятся, следовательно, и вся длина цилиндра останется прежней.
4) Образующие цилиндра обратятся в винтовые линии с большим шагом.
Теория кручения круглого бруса
основана на трёх следующих предположениях:
-плоские поперечные сечения бруса остаются плоскими и после деформации;
-радиусы поперечных сечений при деформации остаются прямыми;
-расстояния между поперечными сечениями не изменяются.
Определение напряжений и деформаций при кручении.
При кручении в поперечном сечении бруса под действием крутящего момента Мкр
— возникает касательное напряжение, которое распределяется по радиусу сечения по линейному закону: минимальное напряжение (равное нулю) — в центре сечения, максимальное — на поверхности бруса (рис. 2). Векторы напряжения направлены перпендикулярно радиусу сечения.
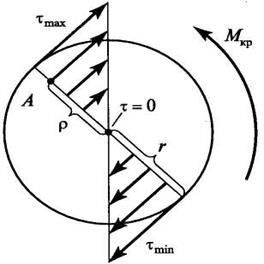
Рис. 2
Касательное напряжение: 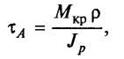
где Мкр
— крутящий момент;
ρ — расстояние от произвольной точки сечения А до центра сечения;
Jp
— полярный момент инерции сечения.
Крутящий момент:
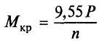 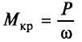
где Р- мощность; n — частота вращения; ω— угловая скорость.
Полярный момент инерции сечения определяется по формулам:
а) для круга (рис. 3, а)
б) для кольца (рис. 3, б)
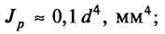
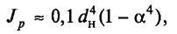
где a=dвн
/dн
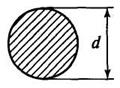 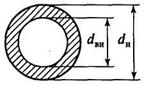
Рис. 3
Выведем формулу τ m
ах
при кручении:
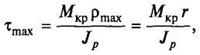
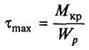
где W = Jp
/r —полярный момент сопротивления сечения (величина, характеризующая способность бруса сопротивляться деформации кручения).
Полярный момент сопротивления сечения определяется по формулам:
для круга:
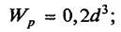
для кольца:
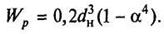
При кручении бруса его ось испытывает скручивание на некоторый угол φ, который называется углом закручивания. Его величина определяется по формуле:
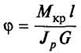
где l — длина бруса; G — модуль сдвига.
Расчеты на жесткость ведутся по единичному углу закручивания, т.е. углу закручивания, приходящемуся на единицу длины бруса:
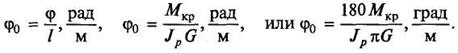
Условие прочности при кручении: рабочее напряжение, возникающее при деформации кручения, должно быть меньше или равно допускаемому напряжению, т.е. 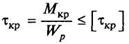
Три расчета на прочность при кручении.
Проверочный.
1. По известным размерам (даны геометрические параметры сечения) и материалу вала (задано [tкр
])проверяется возможность конструкции выдержать заданную нагрузку в виде крутящего момента Т в анализируемом на прочность сечении, используя выражение: tmax
=T/Wр
£[tкр
].
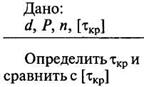
Решение:
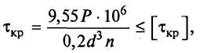
где 106
— переводной коэффициент для мощности, выраженной в киловаттах.
Проектный.
По известному значению крутящего момента в сечении Т и материалу вала ([х]) подбираются необходимые размеры поперечного сечения для обеспечения безопасности работы по величине полярного момента сопротивления
Дано: P, n, [τкр
]
Определить d
Решение:
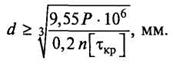
Проверочно-уточненный.
Определение допускаемой внешней нагрузки [Т] (или установление работоспособности). По известным геометрическим параметрам сечения (Wp
— задано) и материалу вала ([t]) находится допускаемая величина внешней нагрузки: [T] = [t]Wp
.
Выбор величины допускаемого напряжения при кручении [t] зависит как от свойств материала вала, так и от принятого коэффициента запаса прочности [n]:
[t]=tпред
/[n]
Для пластического материала при статическом нагружении обычно принимают tпред
=tТ
(предел текучести при сдвиге), а в случае хрупкого материала - tпред
=tВ
(предел прочности). Величина [n] зависит от отрасли техники, назначения и вида конструкции.
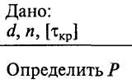
Решение:
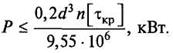
Условие жесткости при кручении
: рабочий единичный угол закручивания должен быть меньше или равен допускаемому углу закручивания, т.е.
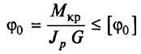
Три расчета на жесткость при кручении.
1. Проверочный
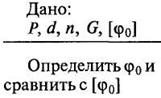
Решение:
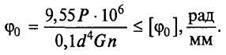
2.
Проектный.
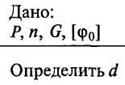
Решение:
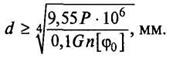
3.
Проверочно-уточненный.
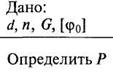
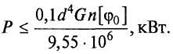
|