Задание 1. Анализ влияния структурных сдвигов на динамику показателей объема продукции и объема производства
Порядок выполнения работы:
Рассчитать индексы постоянного состава, переменного состава и структурных сдвигов (согласно варианту).
Используя графические методы (столбиковые, полосовые, секторные диаграммы) изобразить структуру объема производства (продукции) в стоимостном выражении за сравниваемые периоды.
Сделать выводы по работе.
Таблица 1.1 - Данные об объеме выпуска и цене в базисном и отчетном периодах
| Продукция
|
Базисный период
|
Отчетный период
|
| Выработано, шт
|
Цена за 1 шт., руб
|
Выработано, шт
|
Цена за 1 шт., руб
|
| А
|
3000
|
50
|
4000
|
45
|
| Б
|
4500
|
12
|
4500
|
11
|
| В
|
8000
|
30
|
7000
|
28
|
| Г
|
900
|
65
|
950
|
67
|
1) Рассчитаем индекс цены переменного состава по формуле:
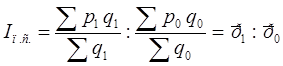 (1.1) (1.1)
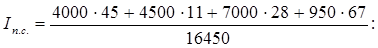
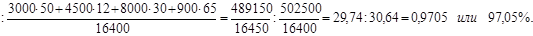
Индекс переменного состава характеризует:
Изменение объема продукции в натуральном выражении,
q
.
Изменение цены на продукцию,
p
(что делает продукцию более или менее выгодной при выполнении плана).
Под влиянием изменения индивидуальных цен и структурных сдвигов в производстве данных изделий средняя цена уменьшилась на 2,95%.
2) Индекс себестоимости фиксированного состава:
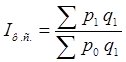 (1.2) (1.2)
Индекс постоянного (фиксированного) состава характеризует изменение объема товарооборота продукции за счет изменения цен.
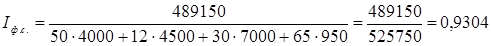 или 93,04% или 93,04%
т.е. под влиянием изменения индивидуальных цен средняя цена снизилась на 6,96%.
Этот, казалось бы, противоречивый результат получился из-за структурных сдвигов.
3) Индекс структуры:
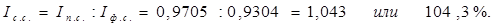
Это значит, что вследствие изменения структуры произведенной продукции цена увеличилась на 4,3%.
4) На рисунках 1.1 и 1.2 отражено изменение количества и цены выработанной продукции в базисном и отчетном периодах.
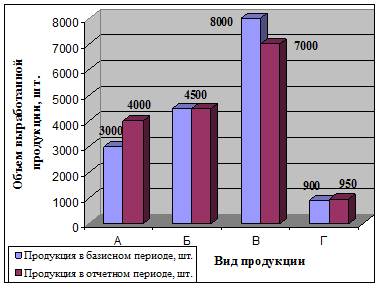
Рисунок 1.1 - Изменение количества выработанной продукции
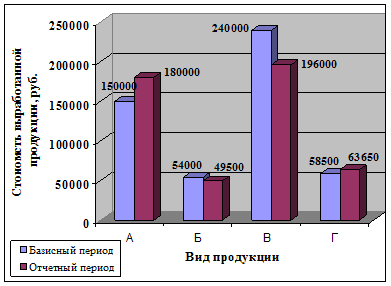
Рисунок 1.2 - Изменение цены выработанной продукции
Задание 2. Корреляционно-регрессионный анализ производительности труда
Порядок выполнения работы:
 Построить вспомогательную таблицу значений у, х1
, х2
, у2
, х1
2
, х2
2
, ух1
, ух2
; х1
х2
. Построить вспомогательную таблицу значений у, х1
, х2
, у2
, х1
2
, х2
2
, ух1
, ух2
; х1
х2
.
Рассчитать парные коэффициенты корреляции ryx
1,
ryx
2
,
rх1
x2
Рассчитать коэффициент множественной корреляции R.
Определить коэффициент множественной детерминации R2
.
Рассчитать параметры a0
;
a1
;
a2
для построения уравнения регрессии.
Построить уравнение регрессии yx
=
a0
+
a1
x1
+
a2
x2
Сделать выводы по работе.
Таблица 2.1
- Данные о среднем проценте выполнения плана, возрасте и стаже работы по профессии работниц
Реклама

| Табельный
номер работницы
|
Средний процент
выполнения нормы выработки yx
|
Возраст, лет
x1
|
Стаж работы
по профессии, лет
x2
|
| 1
|
103,4
|
24
|
10
|
| 2
|
100,3
|
24
|
10
|
| 3
|
106,1
|
28
|
13
|
| 4
|
108,7
|
35
|
15
|
| 5
|
106,6
|
27
|
3
|
| 6
|
105,4
|
27
|
3
|
| 7
|
105,4
|
20
|
3
|
| 8
|
104,5
|
34
|
16
|
| Всего
|
840,4
|
219
|
73
|
1) Построим вспомогательную таблицу значений у, х1
, х2
, у2
, х1
2
, х2
2
, ух1
, ух2
,
x1
x2
Таблица 2.2
- Данные для расчета коэффициентов регрессии
| yx
|
x1
|
x2
|
yx2
|
х1
2
|
x2
2
|
x1
x2
|
yx1
|
yx2
|
уx1
x2
|
| 103,4
|
24
|
10
|
10691,56
|
576
|
100
|
240
|
2481,6
|
1034,0
|
24816
|
| 100,3
|
24
|
10
|
10060,09
|
576
|
100
|
240
|
2407,2
|
1003,0
|
24072
|
| 106,1
|
28
|
13
|
11257,21
|
784
|
169
|
364
|
2970,8
|
1379,3
|
38620,4
|
| 108,7
|
35
|
15
|
11815,69
|
1225
|
225
|
525
|
3804,5
|
1630,5
|
57067,5
|
| 106,6
|
27
|
3
|
11363,56
|
729
|
9
|
81
|
2878,2
|
319,8
|
8634,6
|
| 105,4
|
27
|
3
|
11109,16
|
729
|
9
|
81
|
2845,8
|
316,2
|
8537,4
|
| 105,4
|
20
|
3
|
11109,16
|
400
|
9
|
60
|
2108,0
|
316,2
|
6324
|
| 104,5
|
34
|
16
|
10920,25
|
1156
|
256
|
544
|
3553,0
|
1672,0
|
56848
|
|  840,4 840,4
|
219
|
73
|
88326,68
|
6175
|
877
|
2135
|
23049,1
|
7671,0
|
224919,9
|
2) Рассчитаем парные коэффициенты корреляции ryx
1
,
ryx
2
,
rх1
x2
по формуле:
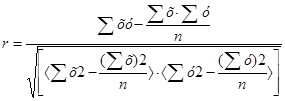 (2.1)
(2.1)
где п
- количество данных, п
= 8.
Значение этого коэффициента изменяется от -1 до +1. отрицательное значение коэффициента корреляции свидетельствует о том, что связь обратная, положительное - связь прямая.
Связь является тем более тесной и близкой к функциональной, чем ближе значение коэффициента к 1.
rх1
= 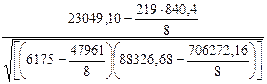 = =  = = 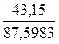 = 0,4926 = 0,4926
r х2
= 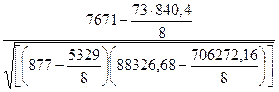 = = 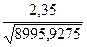 = = 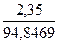 = 0,0248 = 0,0248
r
x1
x2
= 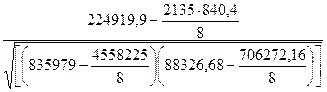 = = 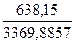 = 0,1894 = 0,1894
Вывод
: полученные коэффициенты находятся в пределах (-1; +1). Это значит, что между производительностью труда у
и возрастом работниц х1
(
0,4926) наблюдается слабая связь (прямая (>0), линейная); между производительностью труда у
и стажем работы по профессии работниц x2 (
0,0248) связь очень слабая - практически отсутствует (прямая (>0), линейная). Связь обоих этих факторов между собой незначительна (0,1894), ее можно охарактеризовать - прямая, линейная. Согласно произведенным расчетам на производительность труда наибольшее влияние оказывает возраст работниц.
3) Рассчитаем коэффициент множественной корреляции по формуле:
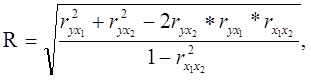 (2.2) (2.2)
где r - линейные (парные) коэффициенты корреляции.
Значение этого коэффициента может изменяться от 0 до 1.
R =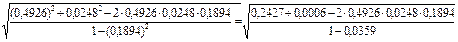 = = 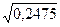 = 0,4975 = 0,4975
Видим, что связь между исследуемыми величинами тесная.
4) Рассчитаем коэффициент множественной детерминации R2
, который показывает, какая доля вариации изучаемого показателя обуславливается линейным влиянием учтенных факторов. Значения коэффициента находятся в переделах от 0 до 1. Чем ближе R2
к 1, тем большим является влияние отобранных факторов на результирующий признак.
Реклама

R2
= 0,2475
Вывод: рассчитанный коэффициент множественной детерминации показывает, что влияние на производительность труда у
возраста работниц х1
и стажа их работы по профессии x2
незначительно.
5) Рассчитаем параметры a0
;
a1
;
a2
для построения уравнения регрессии.
Зависимость среднего процента выполнения нормы выработки от возраста и стажа работы по профессии можно выразить формулой:
yx
=a0
+ a1
x1
+ a2
x2
(2.3)
где yx
- расчетные значения результирующего признака - средний процент нормы выработки;
x1
и x2
- факторные признаки:
х1
- возраст, лет; х2
- стаж работы по профессии, лет;
a0
; a1
; a2
- параметры уравнения.
Для нахождения параметров уравнения a0
; a1
; a2
строится система нормальных уравнений:
na0
+ a1
Σ
x1
+ a2
Σ
x2
= Σ
y
a0
Σ
x1
+ a1
Σ
x1
2
+ a2
Σ
x1
x2
= Σ
yx1
(2.4)
a0
Σ
x2
+ a1
Σ
x1
x2
+ a2
Σ
x2
2
= Σ
yx2
Из таблицы 2.1 Σ x1
= 219, Σ x2
= 73, Σy
= 840,4
Расчеты представим в таблице 2.2
Таблица 2.2
| х1
2
|
x1
x2
|
yx1
|
x2
2
|
yx2
|
| 576
|
240
|
2481,6
|
100
|
1034,0
|
| 576
|
240
|
2407,2
|
100
|
1003,0
|
| 784
|
364
|
2970,8
|
169
|
1379,3
|
| 1225
|
525
|
3804,5
|
225
|
1630,5
|
| 729
|
81
|
2878,2
|
9
|
319,8
|
| 729
|
81
|
2845,8
|
9
|
316,2
|
| 400
|
60
|
2108,0
|
9
|
316,2
|
| 1156
|
544
|
3553,0
|
256
|
1672,0
|
| Σ x1
2
=6175
|
Σ x1
x2
= 2135
|
Σyx1
= 23049,1
|
Σ x2
2
= 877
|
Σyx2
= 7671,0
|
Система уравнений принимает вид:
 8а0
+ 219 а1
+ 73 а2
= 840,4 8а0
+ 219 а1
+ 73 а2
= 840,4
219 а0
+ 6175 а1
+ 2135 а2
= 23049,1
73 а0
+ 2135 а1
+ 877 а2
= 7671,0
Чтобы вычислить значения
a0
;
a1
;
a2
выполняем арифметические действия:
Сократим каждое уравнение на коэффициент при а0
;
 а0
+ 27,3750 а1
+ 9,1250 а2
= 105,0500 а0
+ 27,3750 а1
+ 9,1250 а2
= 105,0500
а0
+ 28, 1963 а1
+ 9,7488 а2
= 105, 2073
а0
+ 29,2465 а1
+ 12,0136 а2
= 105,0835
Произведем вычитания
(2 уравнение - 1 уравнение) и
(3 уравнение - 2 уравнение).
В результате получим систему двух нормальных уравнений с неизвестными а1
и а2
.
0,8213 а1 + 0,6238 а2 = 0,1573
1,0502 а1 + 2,2648 а2 = - 0,1238
При решении новой системы получим:
a2
= 1,8693
a1
= - 1,2282
a0
= 121,6146
Уравнение примет вид:
У = 121,615 - 1,228 x1
+ 1,869 x2
Коэффициенты регрессии дают ответ о том, как изменяется производительность труда при изменении возраста работниц на 1 год (
a1
= - 1,228)
и стажа их работы также на 1 год (
a2
= 1,869
).
При этом следует учитывать, что влияние данных факторов (возраста и стажа работы по профессии) на производительность труда невелико. Это говорит о том, что данная работа не является сложной.
Задание 3. Выявление тренда в динамических рядах
Порядок выполнения работы:
Рассчитать средние уровни ряда
Рассчитать общую среднюю.
Рассчитать индексы сезонности.
Построить на графике кривую сезонных колебаний.
Сделать выводы.
Таблица 3.1
- Данные об объеме выпуска продукции за три года
| Месяцы
|
Годы
|
| 1
|
2
|
3
|
| Январь
|
7,4
|
7,8
|
8,3
|
| Февраль
|
7,9
|
8,3
|
8,6
|
| Март
|
8,7
|
9,2
|
9,7
|
| Апрель
|
8,2
|
8,6
|
9,1
|
| Май
|
7,9
|
8,3
|
8,8
|
| Июнь
|
8,2
|
8,7
|
9,1
|
| Июль
|
8,3
|
8,8
|
9,3
|
| Август
|
8,8
|
9,3
|
9,9
|
| Сентябрь
|
8,7
|
8,9
|
9,3
|
| Октябрь
|
8,8
|
8,2
|
9,9
|
| Ноябрь
|
8,3
|
8,8
|
9,8
|
| Декабрь
|
9,0
|
9,5
|
9,3
|
1) Рассчитаем средние уровни ряда. Вычислим и средние уровни за год и средние уровни за месяц. Средние уровни вычисляем путем сложения всех показателей и деления суммы на количество этих показателей. Например, средняя за январь
(
7,4 + 7,8 + 8,3) / 3 » 7,8333
Общая формула выглядит так
Sr=Σ
xi
/
n (3.1)
Здесь
n
- это количество показателей.
Аналогично рассчитываем и другие средние. Результаты расчетов средних значений в таблицу 3.2
Таблица 3.2 - Расчет средних значений выпуска продукции
| Месяцы
|
Годы
|
Среднее за месяц
|
| 1
|
2
|
3
|
| Январь
|
7,4
|
7,8
|
8,3
|
7,8333
|
| Февраль
|
7,9
|
8,3
|
8,6
|
8,2667
|
| Март
|
8,7
|
9,2
|
9,7
|
9, 2000
|
| Апрель
|
8,2
|
8,6
|
9,1
|
8,6333
|
| Май
|
7,9
|
8,3
|
8,8
|
8,3333
|
| Июнь
|
8,2
|
8,7
|
9,1
|
8,6667
|
| Июль
|
8,3
|
8,8
|
9,3
|
8,8000
|
| Август
|
8,8
|
9,3
|
9,9
|
9,3333
|
| Сентябрь
|
8,7
|
8,9
|
9,3
|
8,9667
|
| Октябрь
|
8,8
|
8,2
|
9,9
|
8,9667
|
| Ноябрь
|
8,3
|
8,8
|
9,8
|
8,9667
|
| Декабрь
|
9
|
9,5
|
9,3
|
9,2667
|
| Сумма за год
|
101,2
|
106,4
|
114,1
|
107,2333
|
| Среднее за год
|
8,4333
|
8,8667
|
9,5083
|
8,9361
|
2) Рассчитаем общую среднюю. Ее можно рассчитать также по формуле (3.1). Можно суммировать средние по годам и результат делить на три. Можно суммировать средние по месяцам и результат делить на 12. Можно суммировать все 36 данных и результат делить на 36. В любом случае получим ответ, указанный в таблице: y0
= 8,9361.
3) Рассчитаем индексы сезонности по формуле (3.2)
 (3.2) (3.2)
Например, индекс сезонности для января равен: 47,833/48,769≈0,981
Аналогичным образом рассчитаем все индексы сезонности, результаты оформим в виде таблицы 3.3
Таблица 3.3
- Значения индексов сезонности
| Месяцы
|
Годы
|
Среднее за месяц
|
Индекс сезонности
|
| 1
|
2
|
3
|
| Январь
|
7,4
|
7,8
|
8,3
|
7,8333
|
0,8766
|
| Февраль
|
7,9
|
8,3
|
8,6
|
8,2667
|
0,9251
|
| Март
|
8,7
|
9,2
|
9,7
|
9, 2000
|
1,0295
|
| Апрель
|
8,2
|
8,6
|
9,1
|
8,6333
|
0,9661
|
| Май
|
7,9
|
8,3
|
8,8
|
8,3333
|
0,9325
|
| Июнь
|
8,2
|
8,7
|
9,1
|
8,6667
|
0,9698
|
| Июль
|
8,3
|
8,8
|
9,3
|
8,8000
|
0,9848
|
| Август
|
8,8
|
9,3
|
9,9
|
9,3333
|
1,0445
|
| Сентябрь
|
8,7
|
8,9
|
9,3
|
8,9667
|
1,0034
|
| Октябрь
|
8,8
|
8,2
|
9,9
|
8,9667
|
1,0034
|
| Ноябрь
|
8,3
|
8,8
|
9,8
|
8,9667
|
1,0034
|
| Декабрь
|
9
|
9,5
|
9,3
|
9,2667
|
1,0370
|
| Среднее за год
|
8,4333
|
8,8667
|
9,5083
|
8,9361
|
--
|
4) Построим на графике кривую сезонных колебаний. График выполним в программе Microsoft Excel и скопируем его в программу Microsoft Word. График в виде гистограммы это будет выглядеть так:
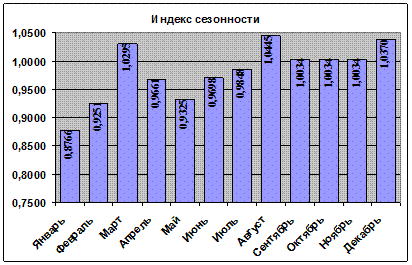
Рисунок 3.1 - Гистограмма средних индексов сезонности
Можно также построить график в виде плавной линии:
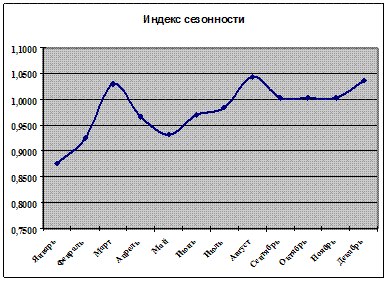
Рисунок 3.2 - График колебаний средних индексов сезонности
5) Выводы:
В данном случае неплохо просматриваются сезонные колебания коэффициентов. Наблюдаются два максимума в марте и августе, а также два ярко выраженных минимума в мае и, особенно, в январе.
Список использованных источников
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. - М.:
2. Финансы и статистика, 1995.
3. Ефимова М.Р., Петрова Е.В., Румянцев В. H. Общая теория статистики: Учебник. - М.: ИHФРА-М, 1996.
4. Ряузов H. H. Общая теория статистики. М., 1990.
5. Адамов В.Е. Экономика и статистика фирм, М., 1996.
6. Статистика коммерческой деятельности: Учебник для вузов/Под ред. И.К. Белявского и О.Э. Башиной. - М.: Финстатинформ, 1996.
7. Э. Кейн. Экономическая статистика и эконометрия.
8. Экономико-математические методы и прикладные модели: Учеб. Пособие для вузов/В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред.В. В. Федосеева. - М.: ЮНИТИ, 1999. - 391 с.
9. Громыко Г.Л. Общая теория статистики: Практикум. - М.: ИНФРА-М, 1999. - 139с.
|