| Содержание
ВВЕДЕНИЕ. 3
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 5
1. Производственные показатели деятельности предприятия и методы их расчета 5
2. Сущность корреляционно-регрессивного метода. 8
2.1. Использование аналитических группировок для расчета показателей тесноты взаимосвязей, коэффициента детерминации и эмпирическое корреляционное отношение. 8
2.2. Метод параллельных рядов. 15
ПРАКТИЧЕСКАЯ ЧАСТЬ. 16
АНАЛИТИЧЕСКАЯ ЧАСТЬ. 28
ЗАКЛЮЧЕНИЕ. 35
СПИСОК ЛИТЕРАТУРЫ.. 37
Под производительностью труда в узком смысле понимают выпуск продукции (полной или добавленной) на единицу затрат живого труда. Этот подход был исторически первым, поскольку на определенной стадии экономического развития, когда труд не вооружен мощнейшими орудиями труда, увеличение производства достигалось главным образом за счет дополнительного увеличения рабочей силы и усиления интенсивности ее использования. По мере накопления основного капитала и оборотных средств, увеличения доли овеществленного труда, очевидной взаимозаменяемости отдельных видов ресурсов живого и овеществленного труда (труд рабочих с успехом стали заменять автоматы, роботы) экономисты пришли к выводу о необходимости учета всех затрат производителя при анализе производительности. Дискуссии о целесообразности и возможности учета овеществленного труда велись в России еще с 20-х годов XX в. В 50-е и последующие годы большой вклад а теоретическую разработку методов измерения производительности труда в широком смысле внесли академики С. Г. Струмилин, В. С. Немчинов, профессор В. В. Новожилов и др. Ими был предложен учет «полной заводской стоимости» как суммы себестоимости и платежей за ресурсы (плата за фонды, проценты за кредит и др.), т. е. всего круга расходов предприятия на изготовление продукции. Однако эти рекомендации не были доведены до практических разработок. И до сегодняшнего дня производительность труда в отечественной практике экономического анализа традиционно рассматривалась как производительность труда в узком смысле слова, как эффективность только одного из производственных ресурсов — ресурсов живого труда.
В современных условиях нестабильной экономической ситуации, инфляции, ограниченной конкуренции, в силу монополизации товарного и сырьевых рынков высокие финансовые результаты зачастую объясняются не столько успехами фирмы, сколько удачно сложившейся конъюнктурой на рынке. Поэтому при измерении производительности на уровне предприятия важно выявить две группы факторов:
Реклама

- факторы, которые отражают реальный уровень и динамику производительности труда и зависят от внутренних технологических и организационных успехов фирмы;
- факторы; отражающие определенные рыночные условия, т. е. уровень и динамику цен на сырье, материалы, энергию, рабочую силу и другие элементы затрат, с одной стороны, и цен на продукцию — с другой (инфляционная компонента).
Цель данной работы – рассмотреть корреляционно-регрессионный анализ взаимосвязей производственных показателей предприятия.
В теоретической части рассмотрены такие вопросы, как сущность и расчет производительности труда, метода измерения уровня и динамики производительности труда, статистические методы анализа производительности труда.
В аналитической части на практике осуществлен анализ производительности труда ряда предприятий сельского хозяйства Калужской области.
Расчеты произведены в программе MS Excel.
1. Производственные показатели деятельности предприятия и методы их расчета
Различают производительность общественного труда, производительность живого (индивидуального) труда, локальную производительность.
Производительность общественного труда определяется как отношение темпов роста национального дохода к темпам роста численности работников сферы материального производства. Рост производительности общественного труда происходит при опережающих темпах роста национального дохода и тем самым обеспечивает повышение эффективности общественного производства.
При росте производительности общественного труда изменяется соотношение между живым и овеществленным трудом. Повышение производительности общественного труда означает уменьшение затрат живого труда на единицу произведенной продукции и увеличение доли прошлого труда. При этом общая сумма затрат труда, заключенного в единице продукции, сохраняется. Эту зависимость К. Маркс назвал экономическим законом роста производительности труда.
Рост индивидуальной производительности труда отражает экономию времени, необходимого на изготовление единицы продукции, или количество дополнительного товара, произведенного за определенный период (минута, час, сутки и т. д.).
Реклама

Локальная производительность - это средняя производительность труда рабочих (работающих), рассчитанная по предприятию в целом или отрасли.
На предприятиях (фирмах) производительность труда определяется как эффективность затрат только живого труда и рассчитывается через показатели выработки (В) и трудоемкости (Тр) продукции, между которыми имеется обратно пропорциональная зависимость.
Выработка — основной показатель производительности труда, характеризующий количество (в натуральных показателях) или стоимость произведенной продукции (товарная, валовая, чистая продукция), приходящиеся на единицу времени (час, смена, квартал, год) или одного среднесписочного работника.
Выработка, рассчитанная в стоимостном выражении, подвержена действию ряда факторов, которые искусственно влияют на изменение выручки, например цена потребляемого сырья, материалов, изменение объема кооперативных поставок и т. п.
В отдельных случаях выработка рассчитывается в нормо-часах. Этот метод называется трудовым и используется при оценке производительности труда на рабочем месте, в бригаде, цехе и т. д.
Изменение производительности труда оценивается путем сопоставления выработки последующего и предшествующего периодов, т. е. фактической и плановой. Превышение фактической выработки над плановой свидетельствует о росте производительности труда.
Выработка рассчитывается как отношение объема произведенной продукции (ОП) к затратам рабочего времени на производство этой продукции (Т) или к среднесписочной численности работников либо рабочих (Ч):
Аналогично определяется часовая (Вч) и дневная (Вдн) выработка на одного рабочего:
Вч=ОПмес
/Тчас
; Вдн
=ОПмес
/Тд,
ОПмес
– объем продукции за месяц (квартал, год);
Тчас
, Тдн
– количество человеко-часов, человеко-дней (рабочего времени), отработанных всеми рабочими за месяц (квартал, год).
При расчете часовой выработки в состав отработанных человеко-часов не включаются внутрисменные простои, поэтому она наиболее точно характеризует уровень производительности живого труда.
При расчете дневной выработки в состав отработанных человеко-дней не включаются целодневные простои и невыходы.
Объем произведенной продукции (ОП) может быть выражен в натуральных, стоимостных и трудовых единицах измерения соответственно.
Трудоемкость продукции
выражает затраты рабочего времени на производство единицы продукции. Определяется на единицу продукции в натуральном выражении по всей номенклатуре изделий и услуг; при большом ассортименте продукции на предприятии определяется по типичным изделиям, к которым приводятся все остальные. В отличие от показателя выработки этот показатель имеет ряд преимуществ: устанавливает прямую зависимость между объемом производства и трудовыми затратами, исключает влияние на показатель производительности труда изменений в объеме поставок по кооперации, организационной структуре производства, позволяет тесно увязать измерение производительности с выявлением резервов ее роста, сопоставить затраты труда на одинаковые изделия в разных цехах предприятия.
Трудоемкость определяется по формуле:
Тр
=Т/ОП
Тр
– трудоемкость
Т – время, затраченное на производство всей продукции, нормо-ч, человеко-ч
ОП – объем произведенной продукции в натуральном выражении.
В зависимости от состава затрат труда, включаемых в трудоемкость продукции, и их роли в процессе производства выделяют технологическую трудоемкость, трудоемкость обслуживания производства, производственную трудоемкость, трудоемкость управления производством и полную трудоемкость.
¨ Технологическая трудоемкость (Ттехн
) отражает затраты труда основных производственных рабочих-сдельщиков (Тсд
) и рабочих-повременщиков (Тповр
):
Ттехн
=Тсд
+Тповр
¨ Трудоемкость обслуживания производства (Тобс
л
) представляет собой совокупность затрат вспомогательных рабочих цехов основного производства (Твспом
) и всех рабочих вспомогательных цехов и служб (ремонтного, энергетического и т.д.), занятых обслуживанием производства (Твсп
):
Тобсл
=Твспом
+Твсп
¨ Производственная трудоемкость (Тпр
) включает затраты труда всех рабочих, как основных, так и вспомогательных:
Тпр
=Ттех
+Тобсл
¨ Трудоемкость управления производством (Ту
) представляет собой затраты труда служащих (руководителей, специалистов и собственно служащих), занятых как в основных и вспомогательных цехах (Тсл.пр
), так и в общезаводских службах предприятия (Тсл.зав
):
Ту
=Ттехн
+Тсл.зав
¨ В составе полной трудоемкости (Тполн
) отражаются затраты труда всех категорий промышленно-производственного персонала предприятия:
Тполн
=Ттехн
+Тобсл
+Ту
В зависимости от характера и назначения затрат труда каждый из указанных показателей трудоемкости может быть:
1. Нормативная трудоемкость
—
это время выполнения операции, рассчитанное на основе действующих норм времени по соответствующим технологическим операциям для изготовления единицы изделия или выполнения работы. Нормативная трудоемкость выражается в нормо-часах. Для перевода ее в фактические затраты времени она корректируется с помощью коэффициента выполнения норм, который увеличивается по мере роста квалификации рабочего.
2. Фактическая трудоемкость
-
это фактические затраты времени одного рабочего на выполнение технологической операции или изготовление единицы изделия в данный период.
3. Плановая трудоемкость
-
это затраты времени одного рабочего на выполнение технологической операции или изготовление единицы изделия, утвержденные в плане и действующие в течение планового периода.
Важный показатель - фондоотдача основных фондов, определяемая как отношение стоимости продукции (валовой, товарной или реализованной) к среднегодовой стоимости основных фондов.
Фо
= Q/Фср
, (12)
где Фо
– фондоотдача;
Q – объём производства и реализации продукции, рублей;
Фср
– среднегодовая стоимость основных производственных фондов предприятия, рублей.
Фондоотдача показывает общую отдачу от использования каждого рубля, затраченного на основные производственные фонды, то есть эффективность этого вложения средств.
В числителе любого показателя производительности находится объем выпущенной продукции. В зависимости от конкретных условий деятельности предприятия, уровня обобщения, наличия информационной базы и аналитических целей применяется один из трех способов измерения объема продукции: натуральный, стоимостный и трудовой. Измерители объема продукции дали название трем методам измерения производительности труда.
Натуральный метод предполагает учет продукции в натуральных или условно-натуральных единицах измерения. Сфера применена этого метода очень ограничена — предприятия, производства, участки, выпускающие однородную продукцию либо наладившие учет затрат труда по каждому виду выпускаемой продукции.
Анализ изменения уровня производительности труда, рассчитанного натуральным методом, производится с помощью индекса:
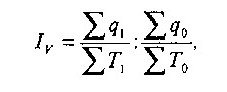
где q0
,q1
— выпуск продукции в натуральном выражении в отчетном и базисном периодах отдельными участками предприятия, производящими однородную продукцию; Т1
, Т0
- затраты труда в отчетном и. базисном периодах.
Поскольку большинство предприятий выпускает разнородный ассортимент продукции, несоизмеримый в натуральном выражении, для определения обобщающих показателей объема продукции используют трудовые и стоимостные соизмерители.
Использование трудовых соизмерителей лежит в основе трудового метода измерения производительности труда. В качестве трудового соизмерителя чаще всего применяют нормативную величину единицы продукции (tH
), В этом случае индекс производительности труда будет иметь вид:
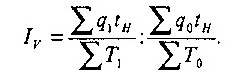
Каждая из дробей в формуле характеризует выработку в нормо-часах на единицу фактических затрат рабочего времени в базисном и отчетном периодах. Легко заметить, что, по существу, это — обратные показатели выполнения норм выработки.
Область применения трудового метода также ограничена - это отдельные участки, бригады, производства, где налажено нормирование труда.
А.И. Ротштейн, один из основоположников отечественной статиcтики промышленности, предложил использовать в качестве трудового соизмерителя продукции трудоемкость единицы продукции базисного периода, а индекс производительности труда рассчитывать по следующей формуле:
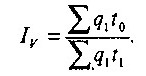
Использование трудового метода для оценки производительности труда возможно лишь там, где ведется учет затрат в разрезе отдельных видов продукции.
Поскольку трудоемкость является мерилом производительности, этот способ измерения динамики производительности труда считается теоретически наиболее обоснованным.
Разность числителя и знаменателя данного индекса позволяет определить абсолютную экономию (дополнительные затраты) рабочего времени в связи с ростом (снижением) производительности труда:

При стоимостном методе измерения уровня и динамики производительности труда объем произведенной продукции оценивается в денежном (стоимостном) выражении. Этот метод является универсальным, поскольку может быть применен на любом предприятии, а также на более высоких уровнях обобщения — на уровне отрасли, региона, экономики в целом.
Формула для расчета индекса производительности труда по стоимостному методу имеет следующий вид [3, C. 100]:
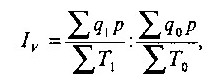
где р — сопоставимые цены.
Если известно изменение производительности труда по отдельным производственным единицам (цехам, участкам, предприятиям, отраслям), то рассчитать обобщающий показатель динамики производительности труда по совокупности производственных единиц в целом можно с помощью среднего арифметического индекса производительности труда, который называют по имени предложившего его академика индексом С. Г. Струмилина:

где iV
- индивидуальные индексы производительности труда по отдельным производственным единицам.
Эффективность использования ОПФ характеризуется следующими показателями:
1. Фондоотдача – Ф0
= Qт
/ F;
где Qт
- товарная продукция;
F – стоимость основных производственных фондов
2. Фондоемкость – Фе
= F / Qт
= 1 / Ф0
;
3. Фондорентабельность – Фр
= Пб
/ F;
где Пб
– балансовая прибыль
4. Фондовооружение труда – Фв
= F / Ч;
где Ч – численность работающих
Формулу фондоотдачи для определения влияния различных факторов можно представить в следующем виде:
Ф0
= Qт
/ F = Fа
/ F х Fд
/ Fа
х 1 /С х Тсм
/ Од
х Тчас
/ Тсм
х Qт
/ Тчас
;
где Fа
– стоимость активной части основных фондов;
Fа
/ F – удельный вес активной части в стоимости основных фондов;
Fд
– стоимость действующего оборудования в активной части;
Fд
/ Fа
– удельный вес действующего оборудования в активной части;
С – средняя цена единицы оборудования;
Тсм
– количество отработанных оборудованием станко – смен;
Од
– число единиц действующего оборудования;
Тсм
/ Од
= количество смен, отработанных единицей оборудования;
Тчас
– количество станко – часов, отработанных оборудованием;
Тчас
/ Тсм
– продолжительность смены в час;
Qт
/ Тчас
– производительность оборудования за 1 станко – час.
Используя данную формулу фондоотдачи и способ цепных подстановок можно установить влияние перечисленных факторов на изменение фондоотдачи в отчетном году по сравнению с базисным.
2. Сущность корреляционно-регрессивного метода
2.1. Использование аналитических группировок для расчета показателей тесноты взаимосвязей, коэффициента детерминации и эмпирическое корреляционное отношение
Для изучения влияния отдельных факторов на динамику производительности труда могут использоваться индексный метод, метод цепных подстановок, метод группировок, корреляционный и другие статистические методы.
Аналитическая группировка позволяет выявить наличие или отсутствие зависимости. Вместе с тем в рамках этого метода не удается аналитически описать эту зависимость, а также не удается выяснить "тесноту" или "существенность" этой зависимости.
Аналитическая группировка может быть равноинтервальной и неравноинтервальной. Сначала выполняется равноинтервальная, а в случае необходимости, т. е. для более наглядного представления зависимости, и неравноинтервальная. В случае положительного результата группировки выявленная зависимость должна быть представлена наиболее наглядно. В примере полученная равноинтервальная группировка не потребовала уточнения, т. е. отсутствовала необходимость в построении неравноинтервальной группировки.
Метод аналитических группировок применяется для выделения особенностей и дифференцированного регулирования по показателям объема и структуры производства, его концентрации, размещения, эффективности и др.
Используя аналитические группировки, прежде всего определяют факторные и результативные признаки изучаемых явлений. Факторные - это признаки, оказывающие влияние на другие, связанные с ними признаки. Результативные -признаки, которые изменяются под влиянием факторных. Чтобы исследовать взаимосвязь между отобранными признаками с помощью метода аналитических группировок, необходимо произвести группировку единиц совокупности по факторному признаку и по каждой группе вычислить среднее значение результативного признака, вариация которого от группы к группе под влиянием группировочного признака будет указывать на наличие или отсутствие взаимосвязи. Группировка позволяет получить такие результаты, по которым можно выявить состав совокупности, характерные черты и свойства типичных явлений, обнаружить закономерности и взаимосвязи.
Нужно выбрать:
1) факторный показатель является количественным признаком, а результативный показатель - качественный признак (например, стаж работы в фирме и квалификация работников (тарифный разряд));
2) основанием группировки является качественный показатель, а результативный показатель - количественный признак (например, тарифный разряд - величина заработной платы);
3) показатель-фактор и показатель-результат являются качественными признаками (например, квалификация работников и уровень их образования);
4) факторный и результативный показатели являются количественными признаками (например, стаж работы и уровень оплаты труда).
При сравнении функциональных и корреляционных зависимостей следует иметь в виду, что при наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака. В отличие от жесткости однозначно функциональной связи корреляционные связи характеризуются множеством причин и следствий и устанавливаются лишь их тенденции.
Необходимо отметить, что экономической теории принадлежит решающее слово в обосновании связей между теми или иными признаками. При этом теоретический анализ должен показать, какие факторы влияют на исследуемый признак или же влияние каких факторов должно быть проверено. Статистическое выражение связи между явлениями может показать, что изменения одного из сопоставляемых признаков сопровождаются изменениями другого. Следовательно, нужно искать объяснение этим изменениям в их содержательном анализе. С помощью статистических методов изучения зависимостей можно установить, как проявляется теоретически возможная связь в данных конкретных условиях. Статистика не только отвечает на вопрос о реальном существовании намеченной теоретическим анализом связи, но и дает количественную характеристику этой зависимости. Зная характер зависимости одного явления от других, можно объяснить причины и размер изменений в явлении, а также планировать необходимые мероприятия для дальнейшего его изменения.
Для того чтобы результаты корреляционного анализа нашли практическое применение и дали желаемый результат, должны выполняться определенные требования в отношении отбора объекта исследования и признаков-факторов. Одним из важнейших условий правильного применения методов корреляционного анализа является требование однородности тех единиц, которые подвергаются изучению методами корреляционного анализа. Например, при корреляционном анализе зависимостей тех или иных технико-экономических показателей работы предприятий от определенных факторов должны быть отобраны предприятия, выпускающие однотипную продукцию, имеющие одинаковый характер технологического процесса и тип используемого оборудования, для предприятий добывающей промышленности определенную роль играет и географическое размещение предприятий.
При выполнении указанных общих требований далее необходима количественная оценка однородности исследуемой совокупности по комплексу признаков. Одним из возможных вариантов такой оценки является расчет относительных показателен вариации. Традиционно широкое распространение для этих целей получил коэффициент вариации. Несколько реже применяется отношение размаха вариации к среднеквадратическому отклонению. Вывод о неоднородности исследуемой совокупности по тому или иному признаку требует проверки гипотезы о принадлежности "выделяющихся" (аномальных) значений признака исследуемой генеральной совокупности.
Другим важным требованием, обеспечивающим надежность выводов корреляционного анализа, является требование достаточного числа наблюдений. Как уже указывалось, влияние существенных причин может быть затушевано действием случайных факторов, "взаимопогашение" влияния которых на результативный показатель в известной мере происходит при выведении средней результативного показателя для массы случаев.
Определенные требования существуют и в отношении факторов, вводимых в исследование. Все множество факторов, оказывающих влияние на величину результативного показателя, к действительности не может быть введено в рассмотрение, да практически в этом и нет необходимости, так как их роль и значение в формировании величины результативного показателя могут иметь существенные различия. Поэтому при ограничении числа факторов, включаемых в изучение, наряду с качественным анализом целесообразно использовать и определенные количественные оценки, позволяющие конкретно охарактеризовать влияние факторов на результативный показатель (к оценкам можно отнести парные коэффициенты корреляции, ранговые коэффициенты при экспертной оценке влияния факторов и др.). Включаемые в исследование факторы должны быть независимыми друг от друга, так как наличие тесной связи между ними свидетельствует о том, что они характеризуют одни и те же стороны изучаемого явления и в значительной мере дублируют друг друга.
Для характеристики тесноты корреляционной связи между признаками в аналитических группировках межгрупповую дисперсию сопоставляют с общей.
Это сопоставление называйся корреляционным отношением и обозначается:
η2
=δ2
/σ2
.
Оно характеризует долю вариации результативного признака, вызванной действием факторного признака, положенного в основание группировки. Корреляционное отношение по своему абсолютному значению колеблется в пределах от 0 до 1. Чем ближе корреляционное отношение к 1, тем большее влияние оказывает факторный признак на результативный. Если же факторный признак не влияет на результативный, то вариация, обусловленная им, будет равна нулю (δ2
= 0) и корреляционное отношение также будет равно нулю (η2
= 0), что говорит о полном отсутствии связи. И наоборот, если результативный признак изменяется только под воздействием одного факторного признака, то вариация, обусловленная этим признаком, будет равна общей вариации (η2
=η2
) и корреляционное отношение будет равно единице (η2
= 1), что говорит о существовании полной связи.
Дисперсионный анализ позволяет не только определить роль случайной и систематической вариаций в общей вариации, но и оценить достоверность вариации, обнаруженной методом аналитических группировок. Определение достоверности вариации дает возможность с заданной степенью вероятности установить, вызвана ли межгрупповая вариация признаком, положенным в основание группировки, или она является результатом действия случайных причин. Для оценки существенности корреляционного отношения пользуются критическими значениями корреляционного отношения η2
при разных уровнях вероятности или значимости α.
Квадрат
множественного коэффициента корреляции называется множественным коэффициентом детерминации
. Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных.
Также это квадрат корреляции Пирсона между двумя переменными (rІ). Он выражает количество дисперсии, общей между двумя переменными.
В случае двух переменных формула для вычисления множественного коэффициента детерминации имеет вид:
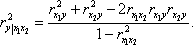
Часто необходимо корректировать коэффициент множественной детерминации на потерю степеней свободы вариации:
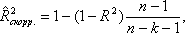
где 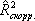 - скорректированное значение множественного коэффициента корреляции; - скорректированное значение множественного коэффициента корреляции;
 - число наблюдений; - число наблюдений;
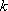 - число переменных, вошедших в модель. - число переменных, вошедших в модель.
Наблюдаемое значение находится по формуле:
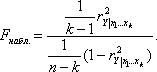
Иногда показателям тесноты связи можно дать качественную оценку (шкала Чеддока
):
| Количественная мера тесноты связи
|
Качественная характеристика силы связи
|
| 0,1-0,3
|
Слабая
|
| 0,3-0,5
|
Умеренная
|
| 0,5-0,7
|
Заметная
|
| 0,7-0,9
|
Высокая
|
| 0,9-0,99
|
Весьма высокая
|
Функциональная связь возникает при значении равном 1, а отсутствие связи - 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50%. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.
2.2. Метод параллельных рядов
Особая роль в выявлении связей не только между качественными, но и количественными признаками принадлежит параллельным статистическим рядам.
Параллельные ряды как метод выявления взаимосвязей пользуются давно. Наличие параллельных рядов признака-фактора (х) и при знака-следствия (у) позволяет выявить и изобразить корреляционные зависимости графически в прямоугольной системе координат.
Если отложить значения х на оси абсцисс, а значение у — на оси ординат и нанести точки соотношений х и у, то мы получим корреляционное поле, где по расположению точек можно судить о характере и степени связи.
Если точки беспорядочно разбросаны по всему полю (а), то какой-либо связи между признаками нет. Если они сосредоточены на оси, направленной снизу вверх и слева направо (б), то имеется прямая зависимость, а если точки распределены сверху вниз и слева направо (в), то зависимость будет обратной. Если точки при прямой или обратной зависимости не расплываются в облаке, а сосредоточены на одной линии (г), то в этом случае мы имеем сильную прямую или обратную связь.
В задание 1 предполагается по данным по 30 предприятиям построить статистический ряд распределения организаций по производительности труда, образовав 5 групп с равными интервалами.
Таблица 1
Исходные данные
| № п/п
|
Среднесписочная численность рабочих, человек
|
Выпуск продукции, млн.руб.
|
ФЗП, млн.руб.
|
Средняя стоимость ОПФ, млн.руб.
|
Уровень производительности труда, тыс.руб./чел.
|
| 1
|
162
|
36,45
|
11,34
|
30,255
|
225
|
| 2
|
156
|
23,4
|
8,112
|
20,124
|
150
|
| 3
|
179
|
46,54
|
15,036
|
38,163
|
260
|
| 4
|
194
|
59,752
|
19,012
|
47,204
|
308
|
| 5
|
165
|
41,415
|
13,035
|
33,546
|
251
|
| 6
|
158
|
26,86
|
8,532
|
22,831
|
170
|
| 7
|
220
|
79,2
|
26,4
|
60,984
|
360
|
| 8
|
190
|
54,72
|
17,1
|
43,776
|
288
|
| 9
|
163
|
40,424
|
12,062
|
33,148
|
248
|
| 10
|
159
|
30,21
|
9,54
|
25,376
|
190
|
| 11
|
167
|
42,418
|
13,694
|
34,359
|
254
|
| 12
|
205
|
64,575
|
21,32
|
51,014
|
315
|
| 13
|
187
|
51,612
|
16,082
|
41,806
|
276
|
| 14
|
161
|
35,42
|
10,465
|
29,753
|
220
|
| 15
|
120
|
14,4
|
4,32
|
12,528
|
120
|
| 16
|
162
|
36,936
|
11,502
|
31,026
|
228
|
| 17
|
188
|
53,392
|
16,356
|
42,714
|
284
|
| 18
|
164
|
41
|
12,792
|
33,62
|
250
|
| 19
|
192
|
55,68
|
17,472
|
43,987
|
290
|
| 20
|
130
|
18,2
|
5,85
|
15,652
|
140
|
| 21
|
159
|
31,8
|
9,858
|
26,394
|
200
|
| 22
|
162
|
39,204
|
11,826
|
32,539
|
242
|
| 23
|
193
|
57,128
|
18,142
|
45,702
|
296
|
| 24
|
158
|
28,44
|
8,848
|
23,89
|
180
|
| 25
|
168
|
43,344
|
13,944
|
35,542
|
258
|
| 26
|
208
|
70,72
|
23,92
|
54,454
|
340
|
| 27
|
166
|
41,832
|
13,28
|
34,302
|
252
|
| 28
|
207
|
69,345
|
22,356
|
54,089
|
335
|
| 29
|
161
|
35,903
|
10,948
|
30,159
|
223
|
| 30
|
186
|
50,22
|
15,81
|
40,678
|
270
|
Для определения групп предприятий определяем размер интервала по производительности труда:
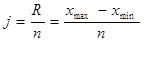 i = R / n = хmax – xmin / n i = R / n = хmax – xmin / n
i = 360 – 120/5 = 48 тыс.руб.
Формируем группы:
| 1
|
120
|
120+48
|
168,00
|
| 2
|
168,00
|
168+48
|
216,00
|
| 3
|
216,00
|
216+48
|
264,00
|
| 4
|
264,00
|
264+48
|
312,00
|
| 5
|
312,00
|
312+48
|
360,00
|
Делаем разноску предприятий по группам. Если значение показателя соответствует значению верхней границы интервала одной группы и нижнему значению границы интервала другой группы, то эту организацию мы относим к последнему.
Таблица 2
Разработанная таблица
| № п/п
|
Группы организации по производительности труда, тыс.руб/чел.
|
Номер организаций
|
| А
|
1
|
| 1
|
До 168
|
5,20,2,6
|
| 2
|
168-216
|
24,10,21,14
|
| 3
|
216-264
|
29,1,16,22,9,18,5,27,11,25,3
|
| 4
|
264-312
|
30,13,17,8,19,23,4
|
| 5
|
312 и выше
|
12,28,26,7
|
| Итого
|
30
|
На основании разработанной таблицы строим ряд распределения.
Таблица 3
Ряд распределения организаций по объему выполненных работ
| № п/п
|
Группы организации по производительности труда, млн.руб/чел.
|
Число предприятий
|
| А
|
1
|
в % к итогу
|
S
|
| 1
|
До 168
|
3,00
|
10,00
|
3,00
|
| 2
|
168-216
|
4,00
|
13,33
|
7,00
|
| 3
|
216-264
|
12,00
|
40,00
|
19,00
|
| 4
|
264-312
|
7,00
|
23,33
|
26,00
|
| 5
|
312 и выше
|
4,00
|
13,33
|
30,00
|
| 30
|
100
|
Наибольшее число организаций сосредоточено в группе с производительностью труда от 216 до 226 тыс.руб./чел – 12 организаций (40,00 %); 7 организаций (23,33%) имеют производительность труда от 264 до 312 тыс.руб./чел; 4 организации (13,33%) – во 2 и 5 группах имеют производительность от 168 до 216 тыс.руб. и от 312 тыс. руб. и выше. 3 организации (10%) – имеют производительность труда до 168 тыс.руб.
Построим графики полученного ряда распределения.
 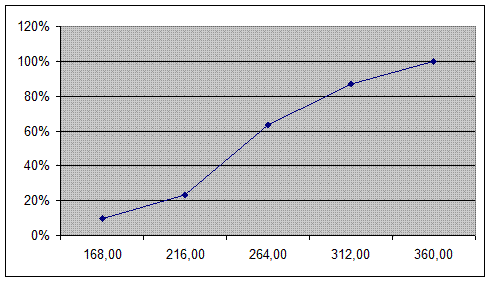
Рис. 1. Кумулята распределения организаций по производительности труда
Ме = 236 тыс.рублей
   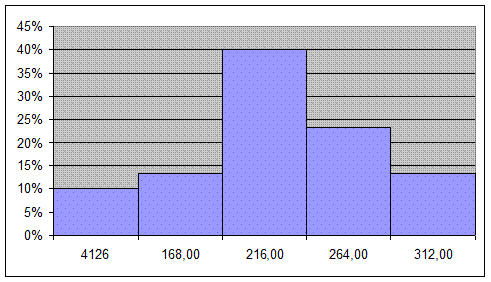
Рис. 2. Гистограмма распределения организаций по производительности труда.
Мо = 245,54 тыс.рублей
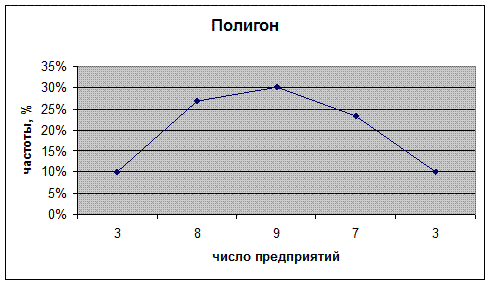
Рис. 3. Полигон распределения организаций по производительности труда.
Ме = 236 тыс.рублей
Мо = 245,54 тыс.рублей
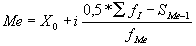
где Х0
- нижняя граница медианного (модального) интервала;
i - величина этого интервала;
SМе-1
- сумма частот, накопленных в интервалах, предшествующих медианному;
¦ Ме
, ¦ Мо
- частота медианного (модального интервала;
¦ Мо-1
, ¦ Мо+1
- частота интервала, предшествующего (следующего) за модальным.
По накопленным частотам определим, что медиана находится в интервале 216 – 264 млн.руб., поскольку его кумулятивная частота равна 19, что превышает половину суммы всех частот.
Тогда по формуле Ме = 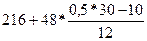 = 236 тыс.руб. = 236 тыс.руб.
Моду Мо 
где Х0
- нижняя граница медианного (модального) интервала;
i - величина этого интервала;
SМе-1
- сумма частот, накопленных в интервалах, предшествующих медианному;
¦ Ме
, ¦ Мо
- частота медианного (модального интервала;
¦ Мо-1
, ¦ Мо+1
- частота интервала, предшествующего (следующего) за модальным.
Мода находится в интервале с наибольшей частотой – т.е. в интервале 2047 – 3807 млн.руб.
Мо = 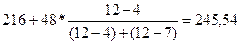 тыс.руб. тыс.руб.
Если данные сгруппированы, то
 = 7440/30 = 248 тыс.рублей/чел. = 7440/30 = 248 тыс.рублей/чел.
где n — объем выборки; k — число интервалов группировки; ni
— частота i-ого интервала; хi
— срединное значение i-ого интервала
Найдем середину интервала и произведение ni
xi
Таблица 4
| Группа
|
Середина интервала
|
ni
xi
|
| 1
|
144,00
|
432
|
| 2
|
192,00
|
768
|
| 3
|
240,00
|
2880
|
| 4
|
288,00
|
2016
|
| 5
|
336,00
|
1344
|
| Итого
|
1200
|
7440
|
Для сгруппированных в интервальный вариационный ряд данных:
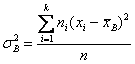
Здесь хi — срединные значения интервалов группировки; 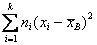 — взвешенная сумма квадратов отклонений. — взвешенная сумма квадратов отклонений.
Таблица 5
| x`-xср
|
(x`-xср
)*n
|
(x`-xср
)2
|
(x`-xср
)2
*n
|
| 104
|
312
|
10816
|
32448
|
| 56
|
224
|
3136
|
12544
|
| 8
|
96
|
64
|
768
|
| 40
|
280
|
1600
|
11200
|
| 88
|
352
|
7744
|
30976
|
| Итого
|
296
|
1264
|
23360
|
87936
|
σ2
= 87936/30 = 2931,2
Стандартным отклонением (или средним квадратическим отклонением) называется корень квадратный из дисперсии:
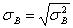 = 54,14 = 54,14
Коэффициент вариации используется и как показатель однородности выборочных наблюдений. Считается, что если коэффициент вариации не превышает 33 %, то выборку можно считать однородной
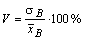 = 54,14/248*100% = 21,83% - выборка однородная. = 54,14/248*100% = 21,83% - выборка однородная.
Для несгруппированных данных среднее арифметическое определяется по следующей формуле:
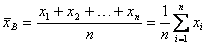 = 7423/30 = 206,19 тыс.руб./чел., где n — объем выборки; хi — варианты выборки. = 7423/30 = 206,19 тыс.руб./чел., где n — объем выборки; хi — варианты выборки.
Для несгруппированных и сгруппированных данных величина среднего арифметического отличается из-за различного способа вычисления: для несгруппированных данных среднее арифметическое определяется по следующей формуле: 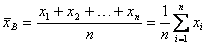 , для сгруппированных - , для сгруппированных -  . Наиболее точная средняя простая арифметическая. Расхождения между средней простой арифметической и средневзвешенной арифметической связано с тем, что при расчете средней простой берутся фактические данные, а при расчете средневзвешенной центральные показатели, рассчитанные как сумма нижней и верхней границы интервала группы деленная на два. . Наиболее точная средняя простая арифметическая. Расхождения между средней простой арифметической и средневзвешенной арифметической связано с тем, что при расчете средней простой берутся фактические данные, а при расчете средневзвешенной центральные показатели, рассчитанные как сумма нижней и верхней границы интервала группы деленная на два.
Задание 2
Используя данные задания 1 построим аналитическую группировку между признаками – фондоотдача и уровнем производительности труда.
Таблица 6
Аналитическая группировка между среднегодовой стоимостью основных фондов и уровнем производительности труда
| Предприятия по фондоотдаче, руб.
|
Число предприятий, ед.
|
Производительность труда, тыс. руб.
|
| всего
|
в среднем на одно предприятие
|
| До 1,18
|
3
|
410,00
|
136,67
|
| 1,18-1,21
|
9
|
1878,00
|
208,67
|
| 1,21-1,24
|
9
|
2319,00
|
257,67
|
| 1,24-1,27
|
3
|
868,00
|
289,33
|
| 1,27 и выше
|
6
|
1248,00
|
208,00
|
| итого
|
30
|
6723,00
|
224,10
|
Таким образом, мы видим, что при росте фондоотдачи производительность труда в среднем на одно предприятие увеличивается.
Построим корреляционную таблицу.
Таблица 7
Корреляционная таблица
| Предприятия по фондоотдаче, руб.
|
Группы предприятий по производительности труда, тыс. руб./чел.
|
| До 168
|
168-216
|
216-264
|
264-312
|
312 и выше
|
| До 1,18
|
3
|
3
|
| 1,18-1,21
|
4
|
5
|
9
|
| 1,21-1,24
|
7
|
2
|
9
|
| 1,24-1,27
|
1
|
2
|
3
|
| 1,27 и выше
|
4
|
2
|
6
|
| 3
|
4
|
12
|
7
|
4
|
30
|
Осуществляем расчет показателей тесноты корреляционной связи между признаками.
Расчет коэффициента детерминации производим по формуле:
η2
= δ2
/σ2
Рассчитываем межгрупповую дисперсию:
δ2
= ∑(у –у)2
f /∑f
Межгрупповая дисперсия рассчитывается по результативному признаку, т.е. производительности труда.
δ2
= (136,67 – 248)2
∙3 + (208,67 – 248)2
∙9 + (267,67 – 248)2
∙9 + (289,33 – 248)2
∙3 + (208 – 248)2
∙6 /30= 5199,65/30 = 173,321
Рассчитываем общую дисперсию:
σ2
= у2
– у2
, где у2
= ∑у2
/n
Делаем разработочную таблицу, где у – сумма прибыли по каждому предприятию.
Таблица 8
| № п/п
|
Производительность труда, тыс. руб./чел , у
|
у2
|
| 1
|
225
|
50625
|
| 2
|
150
|
22500
|
| 3
|
260
|
67600
|
| 4
|
308
|
94864
|
| 5
|
251
|
63001
|
| 6
|
170
|
28900
|
| 7
|
360
|
129600
|
| 8
|
288
|
82944
|
| 9
|
248
|
61504
|
| 10
|
190
|
36100
|
| 11
|
254
|
64516
|
| 12
|
315
|
99225
|
| 13
|
276
|
76176
|
| 14
|
220
|
48400
|
| 15
|
120
|
14400
|
| 16
|
228
|
51984
|
| 17
|
284
|
80656
|
| 18
|
250
|
62500
|
| 19
|
290
|
84100
|
| 20
|
140
|
19600
|
| 21
|
200
|
40000
|
| 22
|
242
|
58564
|
| 23
|
296
|
87616
|
| 24
|
180
|
32400
|
| 25
|
258
|
66564
|
| 26
|
340
|
115600
|
| 27
|
252
|
63504
|
| 28
|
335
|
112225
|
| 29
|
223
|
49729
|
| 30
|
270
|
72900
|
| 7423
|
1938297
|
у2
= ∑у2
/n = 1938297/30 = 64609,9.
σ2
= 64609,9 – 2482
= 64609,9 – 61504 = 3105,9.
η2
= 173,321 /3105,9 = 0,055 или 5,5%.
Корень квадратный из коэффициента детерминации – есть эмпирическое корреляционное отношение.
η = √ η2
η = √0,055 = 0,236.
Коэффициент детерминации свидетельствует о том, что изменение производительности труда на 23,6% определяется изменением фондоотдачи.
Эмпирическое корреляционное отношение свидетельствует о том, что связь между фондоотдачей и производительностью слабая.
3 задание
1. Средняя ошибка выборки для среднего производительности. Выборка 20% бесповторная.
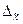 = = 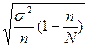 =2* =2* 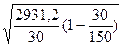 = 8,84 тыс.руб. = 8,84 тыс.руб.
если Р=0,683 то t=1
Средний уровень производительности труда будет находиться в границах, которые мы находим по формуле: 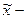 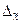 ≤ ≤ 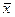 ≤ ≤ 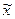 + +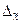
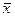 = ∑xd, d = fi/∑fi = 248 тыс.руб. = ∑xd, d = fi/∑fi = 248 тыс.руб.
Следовательно, с вероятностью 0,653 можно утверждать, что средний уровень производительности труда находится в границах
248-8,84≤248≤248+8,84
239,16≤248≤256,84
2. Количество предприятий с уровнем производительности труда 264 тыс.руб. - 11
Доля предприятий со средним уровнем производительности труда свыше 264 тыс.руб. находится в пределах : Выборочная доля составит :
Ω = 11/30 = 0,37
Ошибку выборки определяем по формуле:
где N – объем генеральной совокупности.
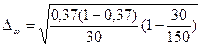 = 0,078 = 0,078
Следовательно с вероятностью 0,653 можно утверждать, что доля предприятий со средним уровнем производительности труда > 264 тыс.руб. будет находиться в следующих пределах:
37% ± 7,8% или 29,2 £ w £ 44,8%
Задание 4
Таблица 9
| t
|
y
|
x
|
y*x
|
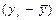 x*x x*x
|
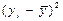
|

|
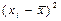
|
ŷ
|
| 1
|
1,15
|
120
|
138
|
14400
|
0,88
|
0,77
|
79,400
|
6304,360
|
0,780739695
|
| 2
|
1,16
|
150
|
174
|
22500
|
0,89
|
0,78
|
109,400
|
11968,360
|
0,972203056
|
| 3
|
1,16
|
140
|
162,4
|
19600
|
0,89
|
0,78
|
99,400
|
9880,360
|
0,908381936
|
| 4
|
1,18
|
170
|
200,6
|
28900
|
0,91
|
0,82
|
129,400
|
16744,360
|
1,099845297
|
| 5
|
1,19
|
190
|
226,1
|
36100
|
0,92
|
0,84
|
149,400
|
22320,360
|
1,227487537
|
| 6
|
1,19
|
220
|
261,8
|
48400
|
0,92
|
0,84
|
179,400
|
32184,360
|
1,418950898
|
| 7
|
1,19
|
228
|
271,32
|
51984
|
0,92
|
0,84
|
187,400
|
35118,760
|
1,470007794
|
| 8
|
1,19
|
180
|
214,2
|
32400
|
0,92
|
0,84
|
139,400
|
19432,360
|
1,163666417
|
| 9
|
1,19
|
223
|
265,37
|
49729
|
0,92
|
0,84
|
182,400
|
33269,760
|
1,438097234
|
| 10
|
1,2
|
225
|
270
|
50625
|
0,93
|
0,86
|
184,400
|
34003,360
|
1,450861458
|
| 11
|
1,2
|
200
|
240
|
40000
|
0,93
|
0,86
|
159,400
|
25408,360
|
1,291308657
|
| 12
|
1,2
|
242
|
290,4
|
58564
|
0,93
|
0,86
|
201,400
|
40561,960
|
1,559357363
|
| 13
|
1,22
|
260
|
317,2
|
67600
|
0,95
|
0,89
|
219,400
|
48136,360
|
1,674235379
|
| 14
|
1,22
|
248
|
302,56
|
61504
|
0,95
|
0,89
|
207,400
|
43014,760
|
1,597650035
|
| 15
|
1,22
|
250
|
305
|
62500
|
0,95
|
0,89
|
209,400
|
43848,360
|
1,610414259
|
| 16
|
1,22
|
258
|
314,76
|
66564
|
0,95
|
0,89
|
217,400
|
47262,760
|
1,661471155
|
| 17
|
1,22
|
252
|
307,44
|
63504
|
0,95
|
0,89
|
211,400
|
44689,960
|
1,623178483
|
| 18
|
1,23
|
251
|
308,73
|
63001
|
0,96
|
0,91
|
210,400
|
44268,160
|
1,616796371
|
| 19
|
1,23
|
254
|
312,42
|
64516
|
0,96
|
0,91
|
213,400
|
45539,560
|
1,635942707
|
| 20
|
1,23
|
276
|
339,48
|
76176
|
0,96
|
0,91
|
235,400
|
55413,160
|
1,776349172
|
| 21
|
1,23
|
270
|
332,1
|
72900
|
0,96
|
0,91
|
229,400
|
52624,360
|
1,7380565
|
| 22
|
1,25
|
288
|
360
|
82944
|
0,98
|
0,95
|
247,400
|
61206,760
|
1,852934516
|
| 23
|
1,25
|
284
|
355
|
80656
|
0,98
|
0,95
|
243,400
|
59243,560
|
1,827406068
|
| 24
|
1,25
|
296
|
370
|
87616
|
0,98
|
0,95
|
255,400
|
65229,160
|
1,903991412
|
| 25
|
1,27
|
308
|
391,16
|
94864
|
1,00
|
0,99
|
267,400
|
71502,760
|
1,980576757
|
| 26
|
1,27
|
315
|
400,05
|
99225
|
1,00
|
0,99
|
274,400
|
75295,360
|
2,025251541
|
| 27
|
1,27
|
290
|
368,3
|
84100
|
1,00
|
0,99
|
249,400
|
62200,360
|
1,86569874
|
| 28
|
1,28
|
335
|
428,8
|
112225
|
1,01
|
1,01
|
294,400
|
86671,360
|
2,152893781
|
| 29
|
1,3
|
360
|
468
|
129600
|
1,03
|
1,05
|
319,400
|
102016,360
|
2,312446582
|
| 30
|
1,3
|
340
|
442
|
115600
|
1,03
|
1,05
|
299,400
|
89640,360
|
2,184804342
|
| Итого
|
8,22
|
1218
|
1434,22
|
221884
|
6,302
|
5,68
|
933,800
|
| среднее
|
0,274
|
40,6
|
47,80733
|
7396,133
|
Уравнение линейной регрессии имеет вид: ŷ = a+b*x. Значение параметров a и b линейной модели определим, используя данные таблицы 9.
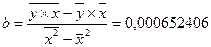
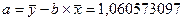
Уравнение линейной регрессии имеет вид ŷ = 1,060573097 + 0,000652406х
Рассчитаем коэффициент детерминации:
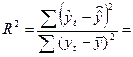 0,880558941 0,880558941
Уравнение регрессии показывает, что при увеличении х в данном случае будет расти и у, то есть существует корреляционная связь между результативным и факторным показателями.
Коэффициент детерминации показывает тесную связь между результативным и факторным показателями.
1. Постановка задачи
Проведем анализ производительности труда сельскохозяйственных предприятий Калужской области. Расчеты выполним в MS Excel. Исходные данные взяты из сборника Города и районы Калужской области. Калуга, 2006. С. 122 – 125.
2. Методика решения задачи
Важное значение в статистических исследованиях коммерческой деятельности имеет индексный метод. Полученные на основе этого метода показатели используются для характеристики развития анализируемых показателей во времени, по территории, изучения структуры и взаимосвязей, выявления роли факторов в изменении сложных явлений.
Индексы широко применяются в экономических разработках государственной и ведомственной статистики.
Статистический индекс - это относительная величина сравнения сложных совокупностей и отдельных их единиц. При этом под сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не подлежат суммированию.
Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально - вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость как потребительских стоимостей и достигается единство.
Индивидуальные индексы характеризуют изменения отдельных единиц статистической совокупности. Так, например, если при изучении оптовой реализации продовольственных товаров определяются изменения в продаже отдельных товарных разновидностей, то получают индивидуальные (однотоварные) индексы.
Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц, образующих статистическую совокупность. Пример, показатель изменения объема реализации товарной массы продуктов питания по отдельным периодам будет общим индексом физического объема товарооборота.
Важной особенностью общих индексов является то, что они обладают синтетическими и аналитическими свойствами.
Синтетические свойства индексов состоят в том, что посредством индексного метода производится соединение (агрегирование) в целом разнородных единиц статистической совокупности.
Аналитические свойства индексов состоят в том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя.
Для определения индекса надо произвести сопоставление не менее двух величин. При изучении динамики социально-экономических явлений сравниваемая величина (числитель индексного отношения) принимается за текущий (или отчетный) период, а величина, с которой производится сравнение - за базисный период.
Основным элементом индексного отношения является индексируемая величина. Под индексируемой величиной понимается значение признака статистической совокупности, изменение которой является объектом изучения.
Рассчитаем индивидуальные индексы производительности труда, а также проведем корреляционно-регрессионный анализ производительности труда.
Корреляционно-регрессионный анализ состоит из таких основных этапов:
— построение системы факторов, которые существенно влияют на результативный признак;
— разработка модели, которая отображает общее содержание взаимосвязей, которые изучаются, и количественная оценка ее параметров;
— проверка качества модели;
— оценка влияния отдельных факторов.
На первом этапе осуществляется отбор факторов, которые существенно влияют на результативный признак.
Он проводится прежде всего исходя из содержательного анализа.
Для получения надежных оценок в модель не следует включать много факторов, их количество не должно быть большее одной трети объема данных, которые анализируются.
3. Технология выполнения компьютерных расчетов
Используем инструмент «Регрессия» пакета MS Excel. Получим на рабочем листе результат корреляционного анализа (таблица 2).
Таблица 2
| Y
|
X0
|
X1
|
| Производительность труда в сельском хозяйстве, тыс.руб.
|
Объем производства в сельском хозяйстве, тыс.руб.
|
Оплата труда в сельском хозяйстве, руб.
|
| Бабынинский
|
1256,2
|
70947,4
|
2263
|
| Барятинский
|
1231,2
|
50699,2
|
3125,3
|
| Боровский
|
1681,1
|
50771
|
3452,2
|
| Дзержинский
|
1210,2
|
60988,2
|
2203,3
|
| Думиничский
|
1279
|
70556,1
|
2088,1
|
| Жиздринский
|
1209,8
|
50822,1
|
2102,3
|
| Жуковский
|
1514,1
|
80366,1
|
2106,3
|
| Износковский
|
1981
|
80166,3
|
1800
|
| Кировский
|
1243,9
|
55913,5
|
2234,3
|
| Козельский
|
1329,2
|
73372,7
|
2100,3
|
| Куйбышевский
|
1181,1
|
10945,5
|
2063,2
|
| Людиновский
|
1128,9
|
38618,6
|
2064,1
|
| Малоярославецкий
|
1263,1
|
29699,4
|
2496,3
|
| Медынский
|
1140,4
|
34276,8
|
2036,3
|
| Мещовский
|
1141,9
|
52477,6
|
2047,2
|
| Мосальский
|
1327,1
|
58366,3
|
2031,2
|
| Перемышльский
|
1247,7
|
26656,36
|
2139,2
|
| Спас-Деменский
|
1299,2
|
32899,2
|
2146,3
|
| Сухиничский
|
1174,1
|
26965,5
|
2036,3
|
| Тарусский
|
1110,2
|
47777,2
|
2088,2
|
| Ульяновский
|
1276,8
|
36888,2
|
2134,2
|
| Ферзиковский
|
1229,9
|
21415
|
2156,3
|
| Хвастовичский
|
1171
|
11897,3
|
2032,2
|
| Юхновский
|
1160,3
|
49968,7
|
2046,3
|
Уравнение регрессии зависимости производительности труда от оплаты труда и выбросов в окружающую среду y = 836,9694 + 0,0048x1
+ 0,099x2
Расчетные показания Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого наблюдения.
Применим инструмент «Регрессия» для регрессионного анализа данных.
Таблица 3
| Регрессионная статистика
|
| Множественный R
|
0,535879
|
| R-квадрат
|
0,287166
|
| Нормированный R-квадрат
|
0,219277
|
| Стандартная ошибка
|
171,5743
|
| Наблюдения
|
24
|
Таблица 4
| Дисперсионный анализ
|
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия
|
2
|
249040
|
124520
|
4,229942
|
0,028601
|
| Остаток
|
21
|
618192,9
|
29437,76
|
| Итого
|
23
|
867232,9
|
Таблица 5
| Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
| Y-пересечение
|
836,9694
|
238,4323
|
3,510302
|
0,002081
|
341,1223
|
1332,817
|
341,1223
|
1332,817
|
| Численность врачей на 1000 человек населения (на конец года) человек
|
0,004843
|
0,001774
|
2,730366
|
0,012535
|
0,001154
|
0,008532
|
0,001154
|
0,008532
|
| Выбросы загрязняющих веществ на человек населения, тонн
|
0,099247
|
0,100132
|
0,991166
|
0,332889
|
-0,10899
|
0,307482
|
-0,10899
|
0,307482
|
Второй столбец таблицы дает нам те коэффициенты уравнения регрессии, которые были найдены, третий столбец содержит ошибки коэффициентов уравнения регрессии.
Таблица 6
| Наблюдение
|
Предсказанное Y
|
Остатки
|
| 1
|
1405,158
|
-148,958
|
| 2
|
1392,678
|
-161,478
|
| 3
|
1425,47
|
255,6304
|
| 4
|
1351,001
|
-140,801
|
| 5
|
1385,905
|
-106,905
|
| 6
|
1291,744
|
-81,9437
|
| 7
|
1435,22
|
78,88007
|
| 8
|
1403,853
|
577,147
|
| 9
|
1329,502
|
-85,6015
|
| 10
|
1400,756
|
-71,556
|
| 11
|
1094,744
|
86,35609
|
| 12
|
1228,852
|
-99,9519
|
| 13
|
1228,551
|
34,54859
|
| 14
|
1205,066
|
-64,6658
|
| 15
|
1294,293
|
-152,393
|
| 16
|
1321,223
|
5,876809
|
| 17
|
1178,373
|
69,32687
|
| 18
|
1209,311
|
89,88864
|
| 19
|
1169,658
|
4,442242
|
| 20
|
1275,598
|
-165,398
|
| 21
|
1227,429
|
49,37112
|
| 22
|
1154,687
|
75,21324
|
| 23
|
1096,277
|
74,72326
|
| 24
|
1282,053
|
-121,753
|
4. Анализ результатов статистических компьютерных расчетов
Анализируя таблицы 3- 5, необходимо отметить, что коэффициент множественной корреляции R=0,53 говорит о том, что связь между показателем и факторами можно считать средней. Коэффициент детерминации утверждает, что вариация результата на 28,71% зависит от вариации факторов.
Критерий Фишера F=0,0286 говорит о том, что уравнение регрессии с вероятностью 0,95 в целом статистически значимое.
Можно видеть, что имеется корреляционная связь между производительностью труда, оплатой труда и выбросами в окружающую среду. Это можно объяснить тем, что заработная плата является одним из главных мотивирующих факторов труда, а выбросы в окружающую среду непосредственно оказывают влияние на самочувствие работников, поэтому важно их свести к минимуму.
Под производительностью труда, как известно, в экономической литературе понимают степень эффективности живого труда, его фактическая способность производить в единицу времени определенное количество потребительских ценностей или количество затраченного времени на производство единицы продукции.
Существует два аспекта статистического изучения производительности труда: изучение производительности только живого труда и изучения производительности труда всего общественного труда - живого и общественного. В наиболее общем виде второй аспект характеризуется снижением доли затрат живого труда и увеличение доли затрат овеществленного труда; причем таким образом, что общая масса затрат труда на производство продукции уменьшается.
В соответствии с принятыми методами определения объема произведенной продукции различают следующие методы измерения производительности труда: 1. натуральный и его разновидности на основе условно-натуральных измерителей продукции; 2. трудовой и его разновидности на основе нормированного и фактически отработанного времени; 3. стоимостный и его разновидности на основе показателей объема продукции (валовой и товарной) и объема (чистой, условной чистой, нормативно чистой продукции, нормативной стоимости обработки, нормативной заработной платы).
Каждый из названных методов имеет самостоятельное значение, свои особенности, определенную сферу применения от правильности выбора соответствующего метода измерения производительности труда зависит достоверность и значение экономических выводов.
Для изучения влияния отдельных факторов на динамику производительности труда могут использоваться индексный метод, метод цепных подстановок, метод группировок, корреляционный и другие статистические методы.
В практической части выполнено задание по расчету производительности труда.
Индексный анализ демонстрирует повышение производительности труда в районах Калужской области.
Анализируя таблицы 3- 5, необходимо отметить, что коэффициент множественной корреляции R=0,53 говорит о том, что связь между показателем и факторами можно считать средней. Коэффициент детерминации утверждает, что вариация результата на 28,71% зависит от вариации факторов.
Критерий Фишера F=0,0286 говорит о том, что уравнение регрессии с вероятностью 0,95 в целом статистически значимое.
Можно видеть, что имеется корреляционная связь между производительностью труда, оплатой труда и выбросами в окружающую среду. Это можно объяснить тем, что заработная плата является одним из главных мотивирующих факторов труда, а выбросы в окружающую среду непосредственно оказывают влияние на самочувствие работников, поэтому важно их свести к минимуму.
1. Города и районы Калужской области. Калуга, 2006.
2. Громыко Г.Л. Статистика. М.: ЮНИТИ-ДАНА, 2001.
3. Козинец Л.С. Темпы роста и структурные сдвиги в экономике. М. Инфра-М, 2001.
4. Курс социально-экономической статистики / Под ред. М.Г.Назарова. М.: «Финансы и статистика», 2000.
5. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности / Под редакцией О.Э. Башиной, А.А. Спирина. М.: Инфра-М, 1999.
6. Статистика / Под. ред. В.М. Гусарова. М.: ЮНИТИ-ДАНА; 2001.
7. Статистика /Под редакцией В.Г. Ионина. М.: ЮНИТИ-ДАНА, 2001.
8. Статистический словарь. М. «Дело», 2001.
9. Теория статистики / Под редакцией Р.А. Шмойловой. М.: «Финансы и статистика», 2002.
10. Экономическая статистика / Под ред. Ю.И. Иванова. М.: Финансы и статистика», 2002.
|