Министерство образования и науки Украины
Харьковский национальный университет радиоэлектроники
Кафедра ЕК
Курсовой проект
по дисциплине «Моделирование экономической динамики»
на тему: «Модель гонки вооружений Ричардсона»
Выполнил:
Ст.гр.ЕКс-10-1
Коновалов А.С.
Проверила:
Новожилова М.В.
Харьков 2010
Постановка задачи
Провести анализ следующих двух моделей гонки вооружения по Ричардсону. Результаты анализа одной модели подтвердить численными расчётами, построив графики x(t), y(t). Для каждой области фазового пространства, задав соответствующие начальные условия, выполнить, по крайней мере, один расчёт.
Первая модель:
| |
Ответное наращивание
|
Износ
|
Недоверие
|
| Синие:
|
1
|
0,8
|
0,1
|
| Зеленые:
|
1
|
1
|
0,1
|
Вторая модель:
| |
Ответное наращивание
|
Износ
|
Недоверие
|
| Синие:
|
1
|
1,2
|
0,1
|
| Зеленые:
|
1
|
1
|
0,1
|
Краткая теория
Модель гонки вооружений Ричардсона
Рассмотрим следующую ситуацию, в которой могут оказаться две враждующие страны. Первая страна ("желтые") вооружается, опасаясь потенциальной угрозы войны с соседней враждебной страной ("зеленые"). В свою очередь "зеленые", зная о росте затрат на вооружение у "желтых", также увеличивают расходы на вооружение. Предположим, что каждая страна изменяет скорость роста (сокращения) вооружений пропорционально уровню затрат другой. Математически эта ситуация может быть смоделирована
следующим образом. Пусть x(t)
- расходы на вооружение "желтых" к моменту t ≥ 0, y(t)
- то же, но "зеленых". Тогда простейшая модель гонки вооружений может быть сформулирована в виде системы двух линейных дифференциальных уравнений с постоянными коэффициентами:
| {
|
dx / dt = ay
,
|
| dy / dt = bx
,
|
(1)
где а
и b
- положительные константы. Эти уравнения описывают положительную обратную связь.
Модель (1) имеет очевидный недостаток: рост затрат на вооружение ничем не лимитируется. Естественно предположить, что чем больше текущий уровень затрат на оборону, тем меньше скорость его роста (отрицательная обратная связь). Получаем следующую систему уравнений:
| {
|
dx / dt = ay-mx
,
|
| dy / dt = bx - пу
,
|
(2)
где а, b, т, п
- положительные константы.
Рассмотрим третий постулат, включенный Л. Ричардсоном в модель: государство наращивает вооружение, руководствуясь своими державными притязаниями и враждебностью к другим государствам, даже если другие страны не угрожают существованию данного государства. Обозначим соответствующие коэффициенты претензии через r
и s
(r
> 0 и s
> 0). Если г<0 и s
< 0, то их можно назвать коэффициентами доброй роли. Получаем следующую систему уравнений:
| {
|
dx / dt = ay - тх + r
,
|
| dy / dt = bx - ny + s
,
|
(3)
Решением системы (3) являются функции x(t)
и y(t)
, определяемые для данных начальных условий х0
, у0
(начальное состояние гонки вооружений).
Элементарный анализ модели. Одним из важнейших свойств, которые "разумно" потребовать от гонки вооружений, является стабильность. Формализуем это требование следующим образом.
Реклама

Уровень затрат на вооружение должен быть постоянным и не зависеть от времени:
dx/dt = dy/dt
= 0, (4)
т.е. желательно, чтобы система находилась в состоянии равновесия.
Условия равновесия для системы (18) записываются в следующем виде:
ау
-
тх
+ r = 0,
(5)
bx - ny + s - 0.
(6)
Из (5) и (6) определим
у = (т/а)х - r/а
(7)
у = (
b
/
n
)х+
s
/
n
(8)
и рассмотрим геометрическую интерпретацию линейного уравнения (7) на фазовой плоскости (х, у)
(рис.1).
Для всех точек прямой G
имеем dx/dt
= 0. Можно сказать, что первое уравнение системы (3) задает горизонтальную компоненту скорости движения точки в фазовой плоскости, а второе уравнение - вертикальную. Ясно, что если в некоторой точке фазовой плоскости dx/dt >
0, то x(t)
возрастает и решение системы движется от этой точки вправо, а если dx/dt <
0, то влево. Аналогично, если dy/dt
> 0 (< 0), то точка движется вверх (вниз).
Из школьного курса алгебры известно, что прямая G делит плоскость (х, у)
на две полуплоскости. Для всех точек одной
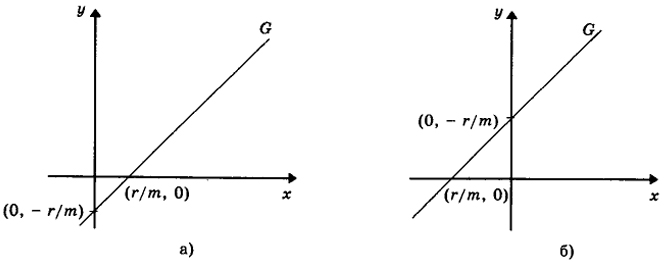
Рис.1. Геометрическая интерпретация уравнения (7): а
- при r >
0; б
- при r < 0
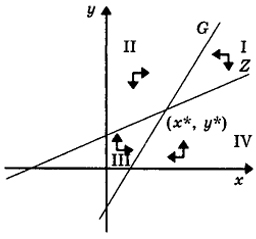
Рис.2. Точка равновесия в первом квадранте
полуплоскости dx/dt
> 0, а другой полуплоскости dx/dt
< 0. То есть первое уравнение системы (3) как бы заставляет точки притягиваться по горизонтали к прямой G
. Аналогичное утверждение верно для второго уравнения этой системы и прямой Z
(вертикальное притяжение) (рис.2). Прямые G
и Z
делят первый квадрант на четыре области, обозначенные римскими цифрами I, II, III, IV.
Рассмотрим поведение модели Ричардсона при t
→∞. Возможны три случая:
1. Бесконечная гонка вооружений: х
→∞ и у
→∞.
2. Взаимное разоружение: х
→ 0, у
→ 0.
3. Равновесие вооружений: х
→ х*, у→ у*
, где у*, х* >
0. Точка равновесия (х*, у*)
находится на пересечении прямых G
[уравнение (5)] и Z
[уравнение (6)] (см. рис.2).
Легко показать, что если r
> 0 и s
> 0,то точка пересечения G
и Z
лежит в первом (см. рис.2) или третьем (рис.3) квадранте.
Стрелки на рис.2-10 показывают горизонтальную и вертикальную составляющие движения точки, находящейся в той или иной области фазовой плоскости. В варианте, показаном на рис.2, из любой начальной точки решение со временем приходит в точку равновесия, достигается "баланс сил", причем независимо от начального уровня вооружений. Из рис.3 видно, что если начальная точка попала в область II, то х
→∞ и у
→∞.
Реклама

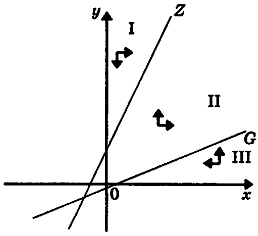
Рис.3. Точка равновесия в третьем квадранте
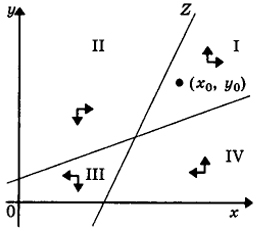
Рис.4. Поведение системы при r
< 0 или (и) s
< 0
Рассмотрим ситуацию, когда по меньшей мере один из коэффициентов r, s
< 0 (рис.4).
Если начальный уровень затрат, т.е. точка (х0
, у0
)
, находится в области I, то гонка вооружений будет бесконечной (х
-"´´, у
-> ´´). Если начальная точка находится в области III, то решение системы (3) также "уходит" от равновесия (х*, у*)
, но зато стремится к точке (0, 0) (взаимное разоружение).
Таким образом, наличие у одного или обоих государств "доброй воли" (r, s
< 0) не гарантирует удовлетворительного исхода гонки вооружений. Все зависит от начального состояния системы.
Очевидно, что поведение модели Ричардсона зависит от соотношения коэффициентов а, b, т, п
и знаков r, s
. Читателю предлагается самостоятельно убедиться, что имеют место четыре возможных случая:
1. Если тп - ab >
0, r >
0, s
> 0, то существует точка равновесия.
2. Если тп - ab <
0, r >
0, s
> 0, то логика модели ведет к неограниченной эскалации гонки вооружений.
3. Если тп - ab >
0, r
< 0, s
< 0, то гарантируется полное взаимное разоружение.
4. Если тп - ab <
0, r
< 0, s
< 0, то пессимистичность или оптимистичность прогноза существенно зависит от начального состояния.
Провести анализ двух моделей гонки вооружения по Ричардсону. Результаты анализа одной модели подтвердить численными расчётами, построив графики x(t), y(t). Для каждой области фазового пространства, задав соответствующие начальные условия, выполнить, по крайней мере, один расчёт.
Первая модель:
| |
Ответное наращивание
|
Износ
|
Недоверие
|
| Синие:
|
1
|
0,8
|
0,1
|
| Зеленые:
|
1
|
1
|
0,1
|
Вторая модель:
| |
Ответное наращивание
|
Износ
|
Недоверие
|
| Синие:
|
1
|
1,2
|
0,1
|
| Зеленые:
|
1
|
1
|
0,1
|
Моделирование проведем на 50 шагах вперед. Проанализируем данные модели.
Первая модель:
Рассмотрим геометрическую интерпретацию уравнений (7) и (8) для указанных параметров на фазовой плоскости (x,y).
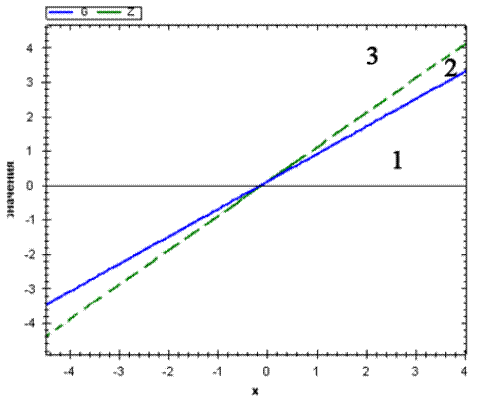
Рисунок 1
Численное решение уравнений дает точку равновесия (-1, -0.9).
Из соотношений (3) определим направление движения по осям:
Для области 1: x>0 (влево), y>0(вверх).
Для области 2: x<0 (вправо), y>0(вверх).
Для области 3: x<0 (вправо), y<0(вниз).
Отсюда можно сделать вывод, что взяв начальные точки в областях 1 и 3, решение перейдет в область два, в которой наблюдается неограниченная эскалация гонки вооружений. Аналогичный результат можно получить, вычислив соотношение mn-ab, при заданных положительных r и s: 0.8-1<0, а это так же означает неограниченную эскалацию вооружений. Т.е. при таких темпах наращивания и темпах износа, модель приходит в состояние неограниченной гонки вооружений.
Проведем аналогичные рассуждения для второй модели:
Графическая интерпретация уравнений (7) и (8) имеет вид:
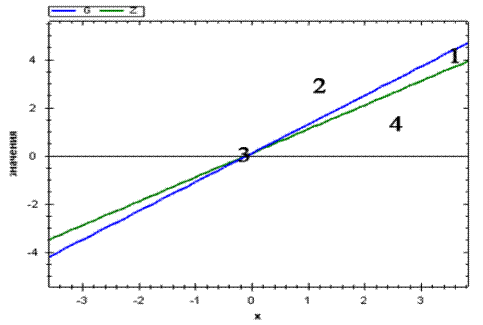
Рисунок 2
Численное решение уравнений дает точку равновесия (1, 1.1).
Из соотношений (3) определим направление движения по осям:
Для области 1: x<0 (влево), y<0(вниз).
Для области 2: x>0 (вправо), y<0(вниз).
Для области 3: x>0 (вправо), y>0(вверх).
Для области 4: x<0 (влево), y>0(вверх).
Отсюда можно вделать вывод, что какими бы ни были начальные условия – система придет к точке равновесия, что так же подтверждается численно: mn-ab>0. То есть при заданных параметрах и любых начальных условиях система придет к точке равновесия.
Рассмотрим графическое решение второй модели для всех областей.
Область 1, точка (2, 2). Графическое решение представлено на рис. 3.
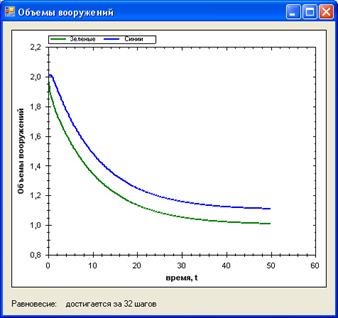
Рисунок 3
Как видно из графика – за 32 шаг достигается точка равновесия. Это объясняется тем, что в начальный момент времени значение объема вооружения первого и втого государства совпадают и решение сначала уменьшается, а через 32 шага достигает равновесного состояния.
Область 2, точка (4, 2.5). Графическое решение представлено на рис. 4.
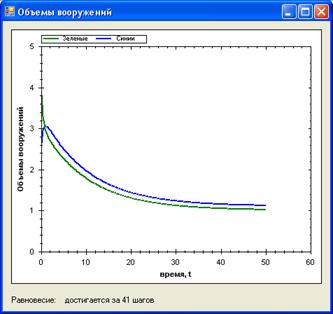
Рисунок 4
Как видно из графика – за 41 шаг достигается точка равновесия. Это объясняется тем, что в начальный момент времени значение объема вооружения первого государства значительно больше вооружения второго. Затем, пока объем вооружения зеленых снижается, сини наращивают объем, это продолжается до тех пор, пока объемы не совпадут. Затем наблюдается одновременный спад и установление стабильного режима через 41 шаг (установление стабильного режима определятся с погрешностью 0.0001).
Область 3, точка (0.1, 0.1). Графическое решение представлено на рис. 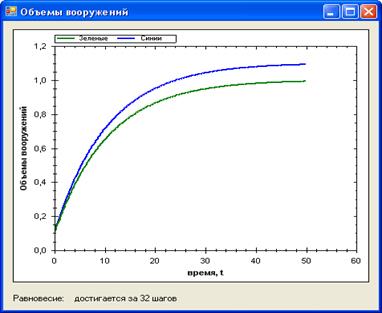
Рисунок 5
Здесь ситуация аналогична предыдущему случаю – из-за того, что начальные условия близки, в начале возникает одновременный рост объема вооружений, а спустя 32 шага – устанавливается равновесное состояние.
Область 4, точка (1, 4). Графическое решение представлено на рис. 6.
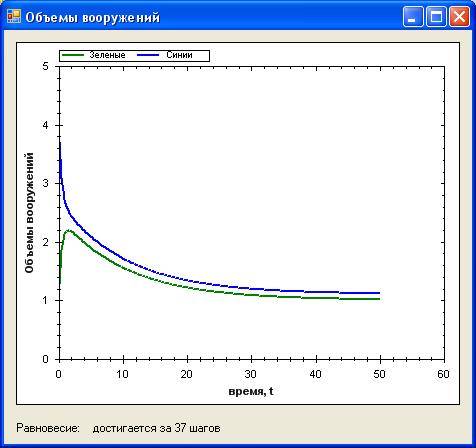
Рисунок 6
В данной ситуации из-за того, что начальные условия сильно различаются наблюдается – в начале рост первого и спад второго решения, а затем постепенный вход на равновесное состояние. Состояние равновесия достигается через 37 шагов.
Выводы
Теоретические данные подтверждены практически: для указанных параметров системы действительно существует точка равновесия, причем система достигает равновесия при любых начальных условиях.
|