| Задача 15
. Найти производную 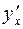 . .
15.1. 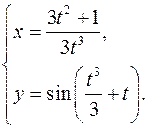
x'= 6t*t3
-3t2
(3t2
+1)
= -t2
-1
3t6
t4
y'= cos(t3
/3+t)(t2
+1)
y'x
= cos(t3
/3+t)(t2
+1)t4
= -t4
cos(t3
/3+t)
-t2
-1
15.2. 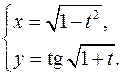
x'= -t _
√(1-t2)
y'= 1 _
2√(1+t)cos2
√(1+t)
y'x
= -√(1-t2
)
= -√(1-t2
) _
2t√(1+t)cos2
√(1+t) 2tcos2
√(1+t)
15.3. 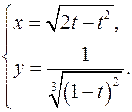
x'= 1-t _
√(2t-t2
)
y'= 2 _
3 3
√(1-t)5
y'x
= 2√(2t-t2
)
= 2√(2t-t2
) _
3 3
√(1-t)5
(1-t) 3 3
√(1-t)2
(1-t)2
15.4. 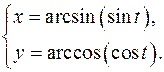
x'= cost
= 1
√(1-sin2
t)
y'= sint
= 1
√(1-cos2
t)
y'x
= 1
15.5. 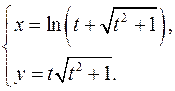
x'= 1+t/√(t2
+1)
= 1 _
t+√(t2
+1) √(t2
+1)
y'= √(t2
+1)+ t2
= 2t2
+1_
√(t2
+1) √(t2
+1)
y'x
= (2t2
+1)√(t2
+1)
= 2t2
+1
√(t2
+1)
15.6. 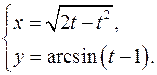
x'= 1-t _
√(2t-t2
)
y'= 1
= 1 _
√(1-(t-1)2
) √(2t-t2
)
y'x
= √(2t-t2
)
= 1_
√(t2-t2
)(1-t) 1-t
15.7. 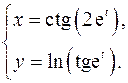
x'= -2et
_
= -2et
_
sin2
(2et
) 4sin2
et
cos2
et
y'= et
= et
_
tget
cos2
et
sinet
coset
y'x
= 4et
sin2
et
cos2
et
= -2sinet
coset
-2et
sinet
coset
15.8. 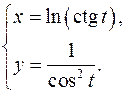
x'= -1
= -1 _
ctgt sin2
t sint cost
y'= 2sint
cos3
t
y'x
= -cos3
t
= -1/2*ctg2
t
2sin2
tcost
15.9. 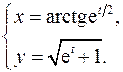
x'= et/2
_
2(1+et
)
y'= et
_
2√(1+et
)
y'x
= 2et
(1+et
)
= √(et
+e2t
)
2et/2
√(et
+1)
15.10. 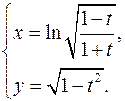
x'= √(1+t)
*√(1+t)
*-1-t-1+t
= -1_
√(1-t) 2√(1-t) (1+t)2
1-t2
y'= -t _
√(1-t2
)
y'x
= t(1-t2
)
= t√(1-t2
)
√(1-t2
)
15.11. 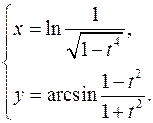
x'= 2t3_
1-t4
y'= (1+t2
)(-2t(1+t2
)-2t(1-t2
))
= -2
√(1+2t2
+t4
-1+2t2
-t4
)(1+t2
)
y'x
= -2(1-t4
)
= t4
-1
2t3
t3
15.12. 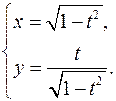
x'= -t _
√(1-t2
)
y'= √(1-t2
)+t2
/√(1-t2
)
= 1 _
1-t2
(1-t2
)3/2
y'x
= -√(1-t2
)_
= 1_
t(1-t2
)3/2
t3
-t
15.13. 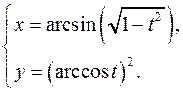
x'= -t
= -1 _
√(1-1+t2
)√(1-t2
) √(1-t2
)
y'= -2arccost
√(1-t2
)
y'x
= 2arccost√(1-t2
)
= 2arccost
√(1-t2
)
15.14. 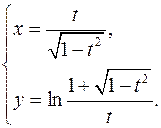
x'= √(1-t2
)+t2
/√(1-t2
)
= 1 _
1-t2
(1-t2
)3/2
y'= t
*-t2
/√(1-t2
)-1-√(1-t2
)
= -1
1+√(1-t2
) t2
t
y'x
= √(1-t2
)
t2
Реклама

15.15. 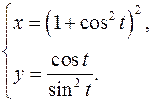
x'= -4(1+cos2
t)costsint
y'= -sin3
t-2cos2
tsint
= -1-cos2
t
sin4
t sin3
t
y'x
= 1+cos2
t
= 1 _
4sin3
t(1+cos2
t)costsint 4sin4
tcost
15.16. 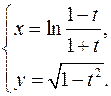
x'= (1+t)(-1-t-1+t)
= -2_
(1-t)(1+t)2
1-t2
y'= -t _
√(1-t2
)
y'x
= -t (1-t2
)_
= t√(1-t2
)
-2√(1-t2
) 2
15.17. 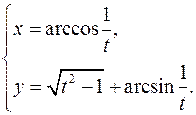
x'= 1
= 1 _
t2
√(1-1/t2
) t√(t2
-1)
y'= t
+ t
= 2t _
√(t2
-1) √(t2
-1) √(t2
-1)
y'x
= 2t2
√(t2
-1)
= 2t2
√(t2
-1)
15.18. 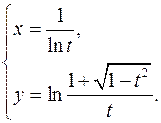
x'= 1_
tln2
t
y'= t
*-t2
/√(1-t2
)-1-√(1-t2
)
= -1
1+√(1-t2
) t2
t
y'x
= -tln2
t
= -ln2
t
t
15.19. 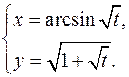
x'= 1 _
2√t√(1-t)
y'= 1 _
4√t√(1+√t)
y'x
= 2√t√(1-t)
= √(1-√t)
4√t√(1+√t) 2
15.20. 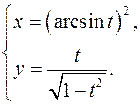
x'= 2arcsint
√(1-t2
)
y'= √(1-t2
)+t2
/√(1-t2
)
= 1 _
1-t2
(1-t2
)3/2
y'x
= √(1-t2
)
= 1 _
2(1-t2
)3/2
arcsint 2(1-t2
)arcsint
15.21. 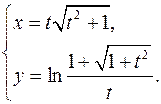
x'= √(t2
+1)+t2
/√(t2
+1) = 2t2
+1
√(t2
+1)
y'= t
*-t2
/√(1-t2
)-1-√(1-t2
)
= -1
1+√(1-t2
) t2
t
y'x
= -√(t2
+1)
= -1 _
(2t2
+1)√(t2
+1) 2t2
+1
15.22. 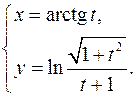
x'= 1/(1+t2
)
y'= (t+1)(t(t+1)/√(t2
+1)-√(1+t2
))
= t-1 _
√(1+t2
)(1+t) √(t2
+1)(1+t)
y'x
= (t-1)(1+t2
)
= (t-1)√(1+t2
)
√(1+t2
)(t+1) 1+t
15.23. 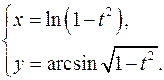
x'= -2t/(1-t2
)
y'= -t
= -1/√(1-t2
)
√(1-1+t2
)√(1-t2
)
y'x
= 1-t2
= √(1-t2
)
2t√(1-t2
) 2t
15.24. 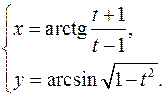
x'= (t-1)2
(t-1-t-1)
= -1_
((t-1)2
+(t+1)2
)(t-1)2
t2
+1
y'= -t
= -1/√(1-t2
)
√(1-1+t2
)√(1-t2
)
y'x
= t2
+1_
√(1-t2
)
15.25. 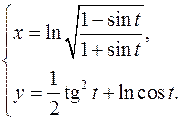
x'= √(1+sint)√(1+sint)(-cost(1+sint)-cost(1-sint))
= -1_
2√(1-sint)√(1-sint)(1+sint)2
cost
y'= tgt/cos2
t-tgt= tg3
t
y'x
= -tg3
tcost
15.26. 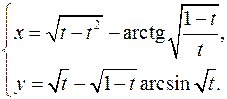
x'= 1-2t
_ t√t(-t-1+t)
= √(1-t)
2√(t-t2
) 2(t+1-t)√(1-t)t2
2√t
y'= 1
+ arcsin√t
_ √(1-t)
= arcsin√t
2√t 2√(1-t) 2√t√(1-t) 2√(1-t)
y'x
= 2√t arcsin√t
= √t arcsin√t
2(1-t) (1-t)
15.27. 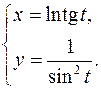
x'= 1
= 1 _
tgtcos2
t sintcost
y'= -2cost
sin3
t
y'x
= -2cost
= -2_
sin4
tcost sin4
t
15.28. 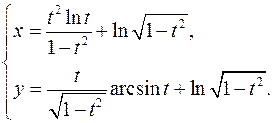
x'= (2tlnt+t)(1-t2
)+2t3
lnt
– 2t
= 2tlnt
(1-t2
)2
2√(1-t2
) (1-t2
)
y'= √(1-t2
)+t2
/√(1-t2
)
arcsint + t/(1-t2
) – t/(1-t2
) = arcsint
1-t2
(1-t2
)3/2
Реклама

y'x
= arcsint(1-t2
)2
= arcsint√(1-t2
)
2tlnt(1-t2
)3/2
2tlnt
15.29. 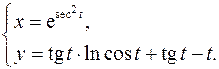
x'= 2esec^2t
sec2
t tgt= 2esec^2t
sint
cos3
t
y'= lncost
_ sint
+ 1/cos2
t-1= lncost-sintcost+sin2
t
cos2
t cost cos2
t
y'x
= 1/2*e-sec^2t
ctgt(lncost-sintcost+sin2
t)
15.30. 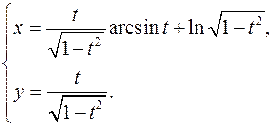
x'= √(1-t2
)+t2
/√(1-t2
)
arcsint + t/(1-t2
) – t/(1-t2
) = arcsint
1-t2
(1-t2
)3/2
y'= √(1-t2
)+t2
/√(1-t2
)
= 1 _
1-t2
(1-t2
)3/2
y'x
= (1-t2
)3/2
= 1 _
(1-t2
)3/2
arcsint arcsint
15.31. 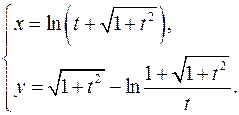
x'= 1+t/√(t2
+1)
= 1 _
t+√(t2
+1) √(t2
+1)
y'= t
_ t
*-t2
/√(1-t2
)-1-√(1-t2
)
= t
+ 1
= t2
+2√(1-t2
)
2√(1+t2
) 1+√(1-t2
) t2
2√(1+t2
) t 2t√(1-t2
)
y'x
= (t2
+2√(1-t2
))√(1+t2
)
2t√(1-t2
)
|