|
Логические операции
.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Выделяют следующие логические операции: инверсия; конъюнкция; дизъюнкция; импликация; эквиваленция.
1. Операция инверсия (отрицание):
Отрицание
- это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Обозначается:
В естественном языке:
соответствует словам "неверно, что..."
и частице "не"
Диаграмма Эйлера-Венна:
Принимаемые значения:
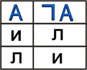
| Диаграмма Эйлера-Венна:
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества соответствует множество, дополняющее его до универсального множества.
|
|
| |
|
| |
|
Пример:
Луна — спутник Земли (А)
. Луна — не спутник Земли (
 A)
2. Операция конъюнкция (лат. conjunctio — соединение) (логическое умножение):
Конъюнкция
- это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Обозначается:
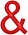
В естественном языке:
соответствует союзу "и"
Принимаемые значения:
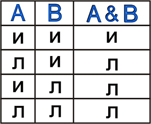
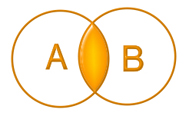
| Диаграмма Эйлера-Венна:
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
|
|
| |
|
| |
|
Примеры:
1. 10 делится на 2 (A - и)
. 5 больше 3 (B - и)
. 10 делится на 2 и 5 больше 3 (A
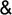 B - и)
.
2. 10 не делится на 2 (A - л)
. 5 больше 3 (B - и)
. 10 не делится на 2 и 5 больше 3 (A
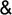B - л)
.
3. 10 делится на 2 (A - и)
. 5 не больше 3 (B - л)
. 10 делится на 2 и 5 не больше 3 (A
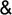 B - л)
.
4. 10 не делится на 2 (A - л)
. 5 не больше 3 (B - л)
. 10 делится на 2 и 5 больше 3 (A
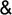B - л)
.
3. Операция дизъюнкция (лат. disjunctio — разделение) (логическое сложение):
Дизъюнкция
- это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
Обозначается:
В естественном языке:
соответствует союзу "или"
Принимаемые значения:
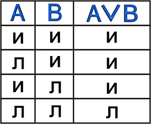
| Диаграмма Эйлера-Венна:
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
|
|
| |
|
| |
|
Примеры:
1. 10 делится на 2 (A - и)
. 5 больше 3 (B - и)
. 10 делится на 2 или 5 больше 3 (A
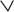 B - и)
.
2. 10 не делится на 2 (A - л)
. 5 больше 3 (B - и)
. 10 не делится на 2 или 5 больше 3 (A
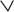B - и)
.
3. 10 делится на 2 (A - и)
. 5 не больше 3 (B - л)
. 10 делится на 2 или 5 не больше 3 (A
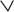B - и)
.
4. 10 не делится на 2 (A - л)
. 5 не больше 3 (B - л)
. 10 не делится на 2 или 5 не больше 3 (A
B - л)
.
4. Операция импликация (лат. лат. implico — тесно связаны) (логическое сложение):
Импликация
- это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
Обозначается:
о
В естественном языке:
соответствует обороту "если ..., то ..."
Принимаемые значения:
л
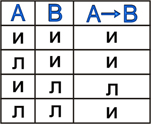
Примеры:
1. Данный четырёхугольник — квадрат (A - и)
. Около данного четырёхугольника можно описать окружность (B - и)
. Если данный четырёхугольник квадрат, то около него можно описать окружность (A
 B - и)
.
2. Данный четырёхугольник — не квадрат (A - л)
. Около данного четырёхугольника можно описать окружность (B - и)
. Если данный четырёхугольник не квадрат, то около него можно описать окружность (A
B - и)
.
3. Данный четырёхугольник — квадрат (A - и)
. Около данного четырёхугольника нельзя описать окружность (B - л)
. Если данный четырёхугольник квадрат, то около него можно описать окружность (A
B - л)
.
4. Данный четырёхугольник — не квадрат (A - л)
. Около данного четырёхугольника нельзя описать окружность (B - л)
. Если данный четырёхугольник не квадрат, то около него нельзя описать окружность (A
B - и)
.
5. Операция эквиваленция (двойная импликация):
Эквиваленция
– это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Обозначается:
о
В естественном языке:
соответствует оборотам речи "тогда и только
тогда"
; "в том и только в том случае"
Принимаемые значения:
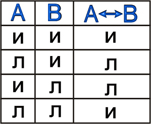
Примеры:
1. 24 делится на 6 (A - и)
. 24 делится на 3 (B - и)
. 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A
 B - и)
.
2. 24 не делится на 6 (A - л)
. 24 делится на 3 (B - и)
. 24 не делится на 6 тогда и только тогда, когда 24 делится на 3 (A
B - л)
.
3. 24 делится на 6 (A - и)
. 24 не делится на 3 (B - л)
. 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A
B - л)
.
4. 24 не делится на 6 (A - л)
. 24 не делится на 3 (B - л)
. 24 не делится на 6 тогда и только тогда, когда 24 не делится на 3 (A
B - и)
.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (“не”), затем конъюнкция (“и”), после конъюнкции — дизъюнкция (“или”) и в последнюю очередь — импликация и эквиваленция.
Логические формулы.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.
Определение логической формулы:
1.
Всякая логическая переменная и символы "истина"
("1"
) и "ложь"
("0"
) — формулы.
2.
Если А
и В
— формулы, то  , (А &В)
, (А v В)
, (А
 B)
, (А
 В)
— формулы.
3.
Никаких других формул в алгебре логики нет.
В п. 1
определены элементарные формулы; в п. 2
даны правила образования из любых данных формул новых формул.
Пример:
Рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог"
.
Обозначим буквой A
высказывание: "купить яблоки"
, буквой B
- высказывание: "купить абрикосы"
,
буквой C
- высказывание: "испечь пирог".
Тогда высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог"
формализуется в виде формулы:
(A v B)
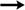C
Формула выполнимая - если при определенных сочетаниях значений переменных она принимает значение "истина"
("1"
) или "ложь"
("0"
).
Как показывает анализ формулы (A v B)
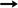C
, при определённых сочетаниях значений переменных A
, B
и C
она принимает значение "истина"
, а при некоторых других сочетаниях — значение "ложь"
.
Некоторые формулы принимают значение “истина” при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v
A
, соответствующая высказыванию “Этот треугольник прямоугольный или косоугольный”
. Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный.
Тавтология - тождественно истинная формула, или формула принимающая значение "истина"
("1"
) при любых входящих в нее значениях переменных.
Логически истинные высказывания
- высказывания, которые формализуются тавтологиями.
В качестве другого примера рассмотрим формулу А &
A
, которой соответствует, например, высказывание “Катя самая высокая девочка в классе, и в классе есть девочки выше Кати”
. Очевидно, что эта формула ложна, так как либо А
, либо A
обязательно ложно.
Противоречие
- тождественно ложная формула, или формула принимающая значение "ложь"
("0"
) при любых входящих в нее значениях переменных.
Логически ложные высказывания
- высказывания, которые формализуются противоречиями.
Равносильные формулы
- две формулы А
и В
принимающие одинаковые значения, при одинаковых наборах значений входящих в них переменных.
Равносильность двух формул алгебры логики обозначается символом  .
Равносильное преобразование формулы
- замена формулы другой, ей равносильной.
|
