Курсовая работа: Методика использования занимательных заданий в процессе обучения математике

Министерство общего и профессионально образования

Южный Федеральный Университет

Ростовский педагогический институт

Кафедра геометрии и методики преподавания математики

Курсовая работа на тему:

Методика использования занимательных заданий в процессе

обучения математике

Выполнила

студентка 62 группы.

Ф-та «Математика»

Недопекина Е.В.

2010 г.

Оглавление

Введение

Глава 1 Занимательные задачи в процессе обучения математике

1.1 Занимательность при обучении математике

1.2 Сущность и типология занимательных задач

1.3 Приемы составления занимательных заданий

Глава 2 Методика использования занимательных заданий в процессе обучения

2.1 Методика использования занимательных заданий на уроках

2.2 Методика использования заданий, составленных с помощью приемов занимательности

2.3 Методика использования занимательных заданий во внеурочное время

Заключение

Список используемой литературы

Приложение

Введение

Ребенок с первых дней занятий в школе встречается с задачей. С начала и до конца обучения в школе математическая задача неизменно помогает ученику вырабатывать правильные математические понятия, глубже выяснять различные стороны взаимосвязей в окружающей его жизни, дает возможность применять изучаемые теоретические положения. В тоже время решение задач способствует развитию младших школьников.

Решение задач занимает в математическом образовании огромное место. Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала.

Современное образование предполагает обучение школьников при наличии у них высокого познавательного интереса. На самом деле лишь небольшое число учащихся изначально имеет интерес к отдельно взятому предмету. Это, как правило, те школьники, у которых есть способности в этой предметной области. Остальные учащиеся нуждаются в формировании интереса к этому учебному предмету или в повышении его уровня.

Познавательный интерес имеет также большую ценность для развития личности.

Проблема познавательного интереса в последнее время все более привлекает внимание не только теоретиков-дидактиков, но и практиков-учителей, что объясняется снижением интереса к учению у некоторой части школьников.

Считается, что интерес выступает как мощный побудитель активности личности, под влиянием которого все психические процессы протекают особенно интенсивно, а деятельность становится увлекательной и продуктивной.

Очень важно сделать так, чтобы процесс обучения не превращался для учеников в скучное и однообразное занятие.

Задача формирования познавательного интереса очень актуальна для построения учебного процесса, так как школе необходимо привить ученику стремление к постоянному пополнению своих знаний с помощью самообразования, содействовать побуждением расширять свой общий и специальный кругозор.

Важная особенность занимательной математики состоит в том, что она побуждает к работе мысли. Насыщенная задачами, головоломками, вопросами и проблемами, она вовлекает ученика в активное сотрудничество с учителем на уроке, будит любознательность и поощряет его к первым самостоятельным открытиям.

Таким образом, главный фактор занимательности – это приобщение учащихся к творческому поиску, активизация их к самостоятельной исследовательской деятельности.

Умение логически мыслить – важное качество, позволяющее эффективно общаться и понимать друг друга.

Логику можно и нужно развивать, причем осуществлять это нужно с самого детства.

Отличные помощники в этом – кроссворды, загадки, и, конечно же, различные математические занимательные задачи.

Охарактеризуем методологический аппарат исследования:

Объект исследования – занимательные задачи на уроках математики.

Предмет исследования – методика использования занимательных заданий в процессе обучения математики.

Цель исследования заключается в описании методики использования занимательных задач в процессе обучения математике.

Задачи исследования:

- Изучить психолого-педагогическую и методическую литературу по теме исследования.

- охарактеризовать понятие занимательности.

- Выделить сущность и типологию занимательных задач.

- Описать приемы составления занимательных заданий.

-Описать методику использования занимательных заданий на уроках и во внеурочное время.

Данная курсовая работа состоит из введения, двух глав, заключения, списка литературы и приложения.

В первой главе рассматривается понятие занимательности при обучении математике, сущность и типология занимательных задач и приемы их составления. Во второй главе приведены методики использования занимательных задач на уроках и о внеурочное время, а также методика использования заданий, составленных с помощью приемов занимательности.

Глава I Занимательные задачи в процессе обучения математике

1.1 Занимательность при обучении математике

Что такое занимательность? Однозначного ответа на данный вопрос нет. Обработав достаточное количество литературы по педагогике, философии, психологии, частным методикам, можно заключить, что практически все авторы, говоря о занимательности, определяют ее через способность восприятия обучаемыми материала. Упоминаются такие качества занимательности, как привлекательность, притягательность, необычность, оригинальность, вызывание возбуждения и др. В ряде работ указывается, что занимательность может проявляться через определенные формы обучения или специфические средства. Некоторые авторы пытаются объяснить занимательность на примере работы с конкретным средством [23].

Иногда перед учителями встает вопрос: выдал материал в одном классе — ученики активно приступили к работе, у них появился интерес, слышатся оригинальные ответы, а выдал тот же самый материал в другом классе — и наблюдаешь прямо противоположную картину — как были ученики безразличны к предмету, так и остались равнодушными, им не интересно слушать, включаться в обсуждение вопросов. В чем тут дело? Скорее всего, у ваших питомцев нет основы, опираясь на которую они осознают суть подготовленного занимательного материала. В этом и кроется субъективность занимательности, которую многие педагоги предпочитают не замечать, виня при неудачах не себя за незнание основ педагогики и психологии, а саму занимательность и материалы, через которые она включается в обучение. Предлагаемый учебный материал, облекаемый в занимательную форму, должен быть знаком ученикам, но либо его подача осуществляется в необычной форме, либо для решения используются нестандартные приемы [10,с.62].

Существует большое количество организационных форм обучения, через которые можно реализовать занимательность. Наиболее часто такие формы используются в начальной школе — это уроки-путешествия, уроки-сказки, уроки-викторины и т. д.

Обучение – это ремесло, использующее бесчисленное количество маленьких трюков. В методической литературе нет общепринятого определения понятия «занимательность обучения математике». Оно считается интуитивно ясным.

Обучение начинается с дошкольного возраста. Дети обучаются в процессе игры. Дошкольники обучаются, не замечая этого, они думают, что просто играют. Но незаметно для себя считают, складывают, вычитают, более того решают разного рода логические задачи, формирующие определённые логические структуры мышления. Дети любят играть и им это интересно. А дальше на фоне успеха можно переходить и к более сложным иллюстрированным или занимательным задачам.

Знания нужны не ради знаний, а как важная составляющая личности. Основная роль математики – в умственном воспитании, в развитии интеллекта. Результатом обучения математике является определённый стиль мышления. В математике заложены огромные возможности для развития детей в процессе их обучения с самого раннего возраста. Развивающий эффект авторской методики достаточно высок. Необходимо также учитывать, что формирование и развитие логических структур мышления должно осуществляться своевременно. Упущения трудно восполняемы. Известно, что основные логические структуры мышления формируются примерно в возрасте от 5 до 11 лет. Запоздалое формирование этих структур протекает с большими трудностями и часто остаётся незавершенным.

Единственно правильный путь, ведущий к ускорению познания, состоит в применении методов обучения, способствующих ускорению интеллектуального развития (разумеется, без ущерба физическому развитию, а в гармоничном единстве с ним).

Под занимательностью на уроке понимают те компоненты урока (способы подачи учебного материала, а иногда и организации обучения), которое содержит в себе элементы необычного, удивительного, неожиданного, комического, вызывают интерес у школьников к учебному предмету и способствуют созданию положительной эмоциональной обстановке учения.

В дидактике и методике математике уже выдвинуты и обоснованы основные положения, касающиеся занимательности обучения.

Во-первых, всю занимательность обучения, следуя К.Д. Ушинскому, принято делить на «внешнюю» (не связанную с содержанием урока) и «внутреннюю», причем «внутренняя» занимательность предпочтительней «внешней» и удельный вес ее должен постепенно увеличиваться.

Во-вторых, все материалы занимательного характера обычно разбивают на три группы: материалы, занимательные по содержанию; материалы, занимательные по форме; материалы, занимательные и по форме, и по содержанию.

В-третьих, основу занимательности, используемой на уроках, должны составлять задания, непосредственно связанные с программным материалом.

Сделать учебную работу насколько возможно интересной для ребенка и не превратить этой работы в забаву – это одна из труднейших и важнейших задач дидактики. Сознательно и прочно усвоить современный курс математики средней школы без должного прилежания нельзя. Прилежание же зависит от доброй воли, которая ни принуждением не внушается, ни сама не приходит, а является чаще всего вслед за познавательным интересом, который можно развивать посредством решения занимательных задач.

Через занимательность проникает в сознание ученика сначала ощущение прекрасного, а затем, при последующем систематическом изучении математики, и понимание красоты ее методов.

Важная особенность занимательной математики состоит в том, что она побуждает к работе мысли. Насыщенная задачами, головоломками, вопросами и проблемами, она вовлекает ученика в активное сотрудничество с учителем на уроке, будит любознательность и поощряет его к первым самостоятельным открытиям [7,с.45]

1.2 Сущность и типология занимательных задач

В повседневной жизни мы часто слышим: «занимательный материал», «занимательная игра», «занимательная задача». Обычно «занимательное» понимается как увлекательное, интересное, притягивающее к себе. Это происходит прежде всего благодаря необычности, нетрадиционности сюжета, положительно влияющего на эмоциональный настрой аудитории, когда в качестве исходных данных и ситуаций используются вымышленные или реальные персонажи, определенными средствами достигающие заданной цели.

Задачей будем называть некую ситуацию, включающую в себя набор исходных данных, используя которые требуется ответить на поставленный в условии вопрос.

Выделим характерные признаки занимательных задач:

такая задача (как и любая задача вообще) имеет развивающую направленность;

в задаче должны быть использованы нестандартные формы и способы представления данных;

в качестве исходных данных и ситуаций используются вымышленные или реальные персонажи, оперируя которыми требуется достигнуть заданной цели;

это качественная задача, решение которой строится на рассуждении без применения математических выкладок;

задача включает в себя необычно поставленный вопрос.

Существуют различные классификации и типологизации задач, применяемых в учебном процессе, например по способу подачи информации (текстовые, графические, задачи-рисунки), по способу решения (арифметические, алгебраические, геометрические, графические), по содержанию (количественные и качественные), по функциональным возможностям в обучении (задачи с дидактическими функциями, задачи с познавательными функциями, задачи с развивающими функциями) и так далее.

Более близка типологизация, предложенная И.В.Егорченко [6], когда выделяются стандартные прикладные задачи, нестандартные прикладные задачи, нестандартные задачи, не являющиеся прикладными, и материалы, вообще не являющиеся задачами. При этом под «нестандартными» И.В. Егорченко [6] понимает именно занимательные задачи. Последние дополнительно подразделяются в зависимости от нестандартной формы, способа решения и особенностей. При этом учитываются: 1) постановка задачи, 2) процесс решения, 3) представление ответов, 4) осуществление проверки решения.

Наиболее интересны задачи, подпадающие под первый тип. К ним И.В. Егорченко относит:

задачи с лишними, недостающими или противоречивыми данными;

задачи без явной постановки вопроса или с неявной его постановкой;

задачи с нестандартной формой изложения данных (рисунок, схема, диаграмма);

задачи с реккурентным способом постановки данных и условий (когда данные задаются опосредованно, один вопрос через другой);

задачи, направленные на установление взаимосвязи, проведение аналогии, обобщения;

задачи, имеющие нестандартную фабулу постановки и задания вопроса;

задачи в форме игр либо заданий практической или лабораторной работы;

задачи, данные в которых представлены в непривычных (нестандартных) единицах измерения;

задания на нахождение ошибок, подтверждение истинности или обнаружение смысловых противоречий.

Не менее интересна и классификация нестандартных задач, не являющихся прикладными. Среди них И.В. Егорченко [6] называет:

задачи, направленные на поиск взаимосвязей между заданными объектами, процессами или явлениями;

задачи, неразрешимые или не решаемые средствами школьного курса на данном уровне знаний учащихся;

задачи, в которых необходимо:

проведение и использование аналогий, определение различий заданных объектов, процессов или явлений, установление противоположности заданных явлений и процессов или их антиподов;

осуществление практической демонстрации, абстрагирование от тех или иных свойств объекта, процесса, явления или конкретизации той или иной стороны данного явления;

установка причинно-следственных отношений между заданными объектами, процессами или явлениями;

построение аналитическим или синтетическим путем причинно-следственных цепочек с последующим анализом получившихся вариантов;

правильное осуществление последовательности определенных действий, избегая ошибок-«ловушек»;

осуществление перехода от плоскостного к пространственному варианту заданного процесса, объекта, явления или наоборот.

Как нетрудно заметить, количество занимательных задач достаточно велико. Среди их многообразия особо выделяют четыре типа, с успехом применяемые в обучении информатике: задачи-рисунки, логические мини-задачи, задачи-шутки и задачи с неполным условием. В настоящее время в качестве средства обучения в основном применяются задачи двух последних типов.

Задачи первого типа ( задачи-рисунки ) представляют собой рисунки или схемы каких-либо объектов, сделанные в необычных ракурсах, т.е. с тех сторон, с которых данный объект мы видим наименее часто. При решении такой задачи учитель (ведущий, загадывающий) задает аудитории вопросы типа: «Что изображено на рисунке?», «С какой стороны изображен предмет?», - либо вопросы о принадлежности данного объекта кому или чему-либо.

Если обучаемые затрудняются сразу дать правильный ответ, то их следует подвести к нему через систему наводящих подсказок, которые могут быть даны как словесно, так и в виде рисунков. Кроме того, ученики сами могут задавать учителю наводящие вопросы, отвечая на которые (верно, но уклончиво) учитель позволяет им собрать как можно больше полезной информации.

К задачам второго типа ( логическим мини-задачам ) относятся короткие по формулировке задачи; обычно состоящие из единственного предложения-вопроса, где ключевые (как кажется на первый взгляд) данные явно или неявно уводят в сторону от правильного ответа.

К третьему типу принадлежат задачи с завуалированной некорректностью поставленных вопросов, ответы на которые можно дать лишь при определенном уровне знания материала. Обычно такие вопросы «провоцируются диалогом, ведущимся в неуточненном контексте» и в них либо заложена ложная посылка, либо для ответа требуется некоторая дополнительная информация, либо когда неправильно использовано вопросное слово, либо когда в вопросе присутствует шутка, которую обучаемые должны распознать и выдать адекватный ответ.

В некоторых ситуациях при решении задач-шуток допускаются ответы также шутливого характера, не несущие в себе конкретной информации, но такие ответы не должны переходить грань дозволенного в общении учителя с учеником, поэтому здесь требуется особая осторожность. Задача-шутка может состоять из серии вопросов, часть из которых поставлены корректно («правильные»), а один вопрос поставлен некорректно (не обязательно последний по счету!).

Дидактические игры. В игре всегда содержится элемент неожиданности и необычности, решается какая-либо задача, проблема, т.е. игра выполняет на уроке те же функции, что и занимательная задача.

Так как дидактическая игра может носить и репродуктивный, и творческий характер, то можно выделить два вида таких игр: игровая ситуация, когда ученика увлекает форма задания; математическая игра, когда ученика увлекает содержание задания.

Игровая ситуация. В подобных случаях внимание школьников привлекает необычная форма задания или неожиданная организация выполнения задания. Очень часто здесь присутствует соревновательный элемент. Возможности для создания игровых ситуаций чрезвычайно велики. Рассмотрим примеры.

Задумай число. Учитель предлагает каждому ученику задумать число и после этого дает указания, какие действия с этим числом надо произвести. В конце концов, учитель угадывает результат. Учащиеся заинтересованы, хотят узнать, в чем тут дело. Этому желанию и соответствует задание: обосновать «угадывание» ответа.

Назови формулу. Один из учащихся выходит к доске и берет у учителя карточку, на которой записана формула некоторой линейной функции. Один из учеников называет любое значение х. Ученик у доски записывает его в таблицу и, подставив это значение в формулу, записывают соответствующее значение у. Ему называют еще одно значение аргумента, он записывает его в следующую клетку и внизу пишет соответствующее значение функции. Ему могут задать еще несколько значений х. Выигрывает ученик, который первый назовет формулу, записанную на карточке.

Математическое лото. Эту игровую ситуацию можно использовать при проведении обобщающих уроков.

В барабан помещают шарики с номерами пунктов учебника, которые уже изучены. Класс делится на группы, обычно по рядам. Команды составляют по 4 – 5 вопросов по каждому пункту. Вызванный ученик крутит барабан, достает шарик, показывает номер. Соперники задают вопрос. Вопрос оценивается в 1 балл, ответ – в 3 балла. Участвуют все. Затем подсчитывается сумма баллов у каждой группы. Определяется группа победитель. Учащиеся повторяют материал с желанием и интересом.

Приемы занимательности, связанные с подачей задания. Приемы этой группы дают возможность то или иное задание облечь в занимательную форму, способствуя тем самым, развитию познавательной активности учащихся.

Математический герой. В урок вводится какой-либо математический герой, который или решает задание, или предлагает его для решения, или придумывает фокус и т.д.

Например, однажды Витя Верхоглядкин записал выражение 25· х· 4. Потом он вместо х стал подставлять в это выражение по очереди числа 13, 21, 39, 47. Получив значение каждого произведения, он очень удивился тому, что все числа оказались «круглыми». Не могли бы вы объяснить почему?

Необычная запись, чертеж, схема . Ярким примером данного приема является задание, связанное с занимательным квадратом. Занимательный квадрат – это квадрат, разбитый на 9 клеток; в каждую клетку записывается один элемент так, чтобы суммы или произведения всех элементов по любой горизонтали, вертикали удовлетворяли определенному условию ( например, были бы равны одному и тому же элементу).

Задумай. Учитель (ученик) задумывает математический объект, а ученики (учитель) должны отгадать то, что задумано, или то, что связано с задуманным.

Пример. Я задумал два числа. Задайте только один вопрос и, выслушав ответ, скажите, одинакового ли они знака.

Найдите ошибку. Ученику предлагается отыскать ошибку (ошибки) в решении (ответе) одного или нескольких заданий.

Нарушение стереотипа. Старые, неполные знания довлеют над людьми даже после получения новых, более полных знаний. Например, изучая в течении нескольких лет положительные числа, для которых всегда справедливы неравенства х < 2х, с > 1/c , учащиеся с трудом осознают, что при прохождении темы «Отрицательные числа» эти неравенства верны не всегда. Чтобы ускорить понимание этого факта, полезно использовать задания, которые помогают школьникам сделать обобщение.

Ученые приходят к выводу, что умению работать творчески, можно специально учиться. На первых порах желательно познакомиться с опытом творческой деятельности других. Однако этого мало. Узнать новую идею – это не то же самое, что выдвинуть, предложить ее. Основное препятствие на пути поиска нового – шаблонность мышления. Поэтому ученые предлагают на первых этапах творческой деятельности использовать специальные указатели, которые помогают сдвинуть сознание с мертвой точки. Опыт показывает, что среди таких указателей могут быть приемы занимательности.

Возникает вопрос, почему именно занимательность стимулирует создание нового. Оба понятия «творчество» и «занимательность» тесно связаны. Главное заключается в том, что они оба обладают общей важнейшей характеристикой: и то и другое должно быть необычным.

Связь этих понятий подтверждается еще и тем, что они могут взаимно обогащать друг друга. Так, некоторые приемы занимательности сходны с приемами творческого мышления. И те и другие не только дают необычное направление мысли, но и часто являются непосредственным руководством к творческому действию. Таким образом, неожиданно открывается еще одно достоинство занимательного подхода: он помогает выработке творческого мышления.

Достаточно продуктивны следующие общие направления мыслительной деятельности: необычный подход к рассмотрению вопроса; поиск ассоциаций; перенос идеи из другой области знаний; «игра» с объектами и идеями [1,с.43].

1.3 Приемы составления занимательных заданий

Рассматривать занимательность обучения только с учетом связи с учебным материалом и без учета воздействия их на мыслительную деятельность ученика нецелесообразно. Поэтому в основу разбиения материалов занимательного характера необходимо положить два существенных свойства понятия «учебная занимательность»: связь с учебным материалом и воздействие на мыслительную деятельность учащихся.

Получаем следующее разбиение:

- организационная занимательность;

- информационная занимательность;

- внеучебные задания занимательного характера;

- учебные занимательные задания.

Под организационной занимательностью понимают занимательность, связанную с организацией урока и лишь косвенно связанную с учебным материалом. [23]

Например, лучший «решатель» устных упражнений награждается значком «Самый смекалистый» и может носить его до следующего урока. Фамилии лучших «решателей» заносятся в специальный альбом, один из разделов которого озаглавлен «Смекалистые в нашем классе (школе)». Учащимся, блестяще проявившим себя на уроке, предоставляется право решать задачу из специального альбома или из какой-нибудь математической книги.

Под информационной занимательностью понимают информацию учебно-познавательного характера, которая вызывает любопытство учащихся. Обычно эта информация не ставит перед учащимися проблемы, а заставляет их задуматься об общих вопросах математики.

Например, во время изучения понятия степени занимателен и полезен для учащихся будет следующий рассказ: «Представьте себе гору (высотой километр) в миллион раз тверже алмаза. Один раз в миллион лет к горе прилетает птичка и слегка касается клювом камня. В конце концов в результате этих прикосновений гора износится до основания. Трудно представить промежуток времени, необходимый для этого. Однако с помощью степеней записать его легко. Вычисления показали, что это произойдет через 10 лет».

Под внеучебными занимательными заданиями понимают задачи, обычно не связанные непосредственно с программным материалом.

Например, зачеркните все 9 точек четырьмя отрезками, не отрывая карандаша от бумаги.

Под учебными занимательными заданиями понимают задания, непосредственно связанные с программным материалом и способствующие усвоению и закреплению его учащимися.

Например: какие числа можно поставить вместо квадратиков, чтобы получилось верное равенство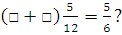

Учебные задания занимательного характера ценны тем, что они наряду с привитием школьникам интереса к учению способствуют также определенному накоплению учебных знаний, умений и навыков.

Занимательные задания можно разбивать и дальше с учетом воздействия их на мыслительную деятельность учащихся. Эти занимательные задания могут быть как репродуктивного, так и творческого характера [23,с.32].

Составляя задачи первого типа (что, впрочем, верно и для трех других типов), нужно прежде всего определить тему, согласно которой делается рисунок, выбирается загадываемый объект, определяется ракурс объекта, под которым обучаемые наблюдают объект наименее часто.

Для помощи в распознавании объектов следует подготовить ряд наводящих подсказок, среди которых может быть упоминание о материале объекта, его области применения, свойствах (вес, цвет, габариты), качественных признаках (мягкий, липкий, холодный) и так далее, но без указания в словесных подсказках названия объекта. Подсказками могут также служить рисунки зашифрованного объекта, выполненные с других ракурсов, либо рисунки объектов, принадлежащих тому же классу, что и отгадываемый. При этом в первом случае изображения объектов не должны быть пространственными, а во втором можно не соблюдать четкость линий и использовать типовые рисунки, но требуется выделять существенные свойства объектов. К ответу ученики могут прийти и посредством наводящих вопросов, которые они сами задают учителю.

Составление задач второго типа после определения соответствующей темы основано на выборе двух или более объектов и одного из свойств или качеств того объекта, который будет фигурировать в правильном ответе. Далее подбирается свойство, принадлежащее другому объекту (другим объектам), и к нему добавляется усиливающее или ослабляющее определение.

Для задач-шуток, которых имеется пять возможных подтипов, требуется учитывать индивидуальные особенности составления (табл. 1).

Таблица 1

Труднее всего составлять занимательные задачи с неполным условием: в них надо предусмотреть такой набор данных, чтобы все они в той или иной степени помогали решить задачу, но часть данных была по возможности скрыта (явно или неявно) от отгадывающего.

Глава II Методика использования занимательных заданий в процессе обучения

2.1Методика использования занимательных заданий на уроках

Под методикой использования занимательных заданий на уроках математики понимаем методы, средства и приемы подачи занимательных задач, занимательные формы организации обучения.

Методика использования учебных занимательных заданий в общих чертах сходна с методикой использования обычных заданий, и, хотя четкой границы между ними провести невозможно, использование занимательности обладает некоторыми особенностями.

Рассмотрим вначале некоторые тенденции в использовании занимательности на уроках математики.

Первая и основная тенденция заключается в том, что учителя автоматически переносят на урок занимательные материалы из внеучебной занимательности, но внеучебные занимательные материалы создавались для других целей, и только редкие из них могут быть использованы на уроках. Необходимо из внеучебной занимательности брать приемы, формы, идеи, а не конкретные материалы.

На основе этого ошибочного подхода в практике учителей появилась и вторая отрицательная тенденция – основное внимание уделяется зрелищности, интересности, увлекательности материалов и совершенно (за редким исключением) игнорируется выполнение ими дидактических функций. Многие учителя поэтому полагают, что роль использования занимательности заключается в том, чтобы поднять тонус учащихся, дать кратковременный отдых и пр. Однако установлено, что работа на уроке, внешне эффективная и нравившаяся и ученикам, и учителю, фактически оказывается бесполезной. Почти все внешне интересные привходящими моментами уроки оказывались в итоге малоэффективными, ибо уводили в сторону от выполнения учебных задач урока.

Третья тенденция, непосредственно вытекающая из второй, заключается в том, что многие учителя не задумываются над вопросом, органично ли входит тот или иной занимательный материал в урок. На уроках порой используется такая занимательность, которая надолго выбивает учащихся из колеи. Другая крайность состоит в том, что учителя используют ограниченное число приемов занимательности. В итоге подача занимательных материалов становится однотипной, что довольно скоро надоедает учащимся и теряет свой эффект.

Наконец, четвертая тенденция заключается в том, что учителя пытаются сами составлять занимательные материалы. А ведь, составляя их, учителя значительно глубже поймут существо занимательности и смогут эффективнее ее использовать как на уроках, так и во внеклассной работе.

Думается, что все это в совокупности и привело к порочной методике использования занимательности на уроках, иногда практикуемой учителями математики. Эта «методика» заключается в следующем. Учитель ограничивается сообщением, что при выполнении плана урока оставшиеся в конце урока несколько минут будут посвящены занимательной математике. Такой подход явно несостоятелен. При этом на первых порах действительно наблюдается возросшее внимание ребят к изучению учебного материала. Однако спустя некоторое время (обычно 2–3 месяца) ученики остывают, и даже занимательные пятиминутки не могут подогреть их интерес к школьной (как они теперь поняли, скучной!) математике. Намного продуктивнее будут уроки, если удастся органично вкраплять занимательный материал в структуру урока, придавать ему дидактические, развивающие и познавательные функции и тем самым уничтожить явную границу между занимательным и учебным материалом.

Таким образом, противопоставление занимательного и учебного материала не дает положительных результатов.

Сформулируем выводы, которые полезно учитывать при использовании занимательных заданий на уроках математики.

Использование занимательных заданий целесообразно тогда, когда есть опасность непринятия учащимися какого-либо учебного задания; при прохождении сложных тем или постановке трудных дидактических задач урока; при выработке умений и навыков учащихся, когда требуется выполнить значительное количество однотипных упражнений; при изучении материала, подлежащего прочному запоминанию.

При этом следует отдавать предпочтение занимательному материалу, отражающему существенные моменты изучаемого, а также занимательным заданиям неоднократного использования.

Для каждого занимательного материала, который предполагается использовать на уроке, учитель должен выяснить: будет ли он занимательным для учащихся данного класса? Органично ли он войдет в структуру урока? Будет ли его использование эффективным?

Учителю надо постараться избежать таких ошибок в использовании занимательности на уроке, как отвлечение от темы и дидактических задач урока (резкий скачок в сторону), неподготовленность занимательного задания предыдущей учебной работой на уроке, отсутствие учета всех категорий учащихся и др.

При включении занимательных задач в учебный процесс нужно помнить, что они не должны выступать прямым стимулом при обучении данной (да и любой другой) дисциплины. Иногда имеет смысл использовать занимательные задачи для эмоциональной разгрузки, но нельзя акцентировать на этом внимание обучаемых. Например, не рекомендуется предварять решение таких задач словами: «А теперь давайте отдохнем (т.е. расслабимся!) и решим занимательную задачу». По мнению М.Ю.Шубы [23]«использование занимательных заданий целесообразно тогда, когда есть опасность неприятия учащимися какого-либо учебного задания; при прохождении сложных тем или при постановке трудных дидактических задач урока; при выработке умений и навыков учащихся, когда требуется выполнить значительное количество однотипных упражнений; при изучении материала, подлежащего прочному запоминанию». Не рекомендуется также выставлять оценку за решение занимательных задач, выбрав в качестве стимула похвалу ученика перед классом (хотя такие ответы обучаемых могут и должны влиять на общую оценку при проверке большого блока материала).

Приведем несколько примеров занимательных задач.

Задачи- шутки.

1. Полторы корзины с грибами стоят полтора рубля. Сколько стоят тринадцать корзинок?

2. Как из четырех спичек получить 15, не ломая их?

3. В танце первый слог найдете,

Цифра- это новый слог.

Ну, а дальше вы возьмете

И приставите предлог.

В целом- тот, кто защищает

Слав, честь страны родной,

Страха он в бою не знает

И в труде- труда Герой.

Задачи с числами.

Записать 80 четырьмя пятерками (5×5+55)

Логические задачи.

В одном классе было много девочек. Мальчики решили узнать, какие цветы им нравятся. После опроса выяснилось, что семерым из девочек нравятся розы, шестерым- георгины, пятерым – ромашки. Четверо любили розы и георгины, трое – розы и ромашки, двое – георгины и ромашки. А одной нравились и розы, и георгины, и ромашки. Сколько девочек было в классе?

Русские задачи.

Веселый француз пришел в трактир с неизвестной суммой денег. Кроме этого он занял у хозяина трактира столько денег, сколько у него уже имелось. Из всей суммы он отдал один рубль. После этого он пошел в другой трактир и опять занял столько денег, сколько у него было, а затем отдал один рубль. В третьем и четвертом трактирах француз сделал то же самое. В результате из четвертого трактира он вышел без денег. Спрашивается, сколько денег было у весельчака француза.

Их можно включать в процесс обучения практически на любом типе и этапе урока. Нужно сказать, что на каждом уроке решать занимательные задачи нецелесообразно, а количество таких задач не должно превышать одной- двух.

2.2 Методика использования заданий, составленных с помощью приемов занимательности

Необычный учебный материал обладает некоторыми особенностями по сравнению с обычным.

Например, обычная схема учебных заданий такова:

Однако, чтобы учащиеся научились решать задачи, вовсе не обязательно всегда избирать этот путь. Иногда полезно нарушать эту схему.

Например, наряду с обычными (и важными) заданиями – выполнить умножение столбиком – рекомендуется использовать иногда видоизмененные задания. Рассмотрим пример.

Вместо звездочек надо записать цифры и в обоих множителях поставить запятые так, чтобы пример был выполнен верно.

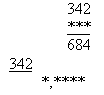
Чтобы восстановить пример, ученик должен проанализировать ситуацию, выделить существенные моменты в ней, вспомнить правила, проявить определенную сообразительность. Проводимый анализ, в свою очередь, ускоряет формирование навыка и запоминание правил. Этим компенсируется некоторая потеря времени по сравнению с обычным заданием (выполнить умножение).

Эта связь между учебными заданиями и догадкой ученика присуща заданиям, составленным с помощью многих приемов занимательности («Обращение», «Зашифрованные задания» и др.).

Их методическая ценность в том, что ученику надо глубже вникать в существо задания, выделять главные моменты, учитывая связи между компонентами, и т. д. Благодаря этому учебный навык, на формирование которого направлено это задание, вырабатывается быстрее, ибо он связан с продуктивной мыслительной деятельностью ученика.

Еще одно достоинство многих занимательных задач заключается в том, что при их решении у ученика часто возникает необходимость менять ход мысли на обратный. Примеров этому было приведено уже достаточно.

Как известно, умение менять ход своей мысли на обратный – ценнейшее качество ума. Занимательные задания способствуют формированию гибкости ума, освобождению мышления от шаблонов.

С помощью приемов занимательности создаются задания, которые могут служить мостиком от стандартных задач к нестандартным.

Известно, что учащиеся с трудом решают нестандартные задачи. Причин этому много. Одна из них заключается в резком переходе от стандартных задач к нестандартным. Необходимы переходные задания. Довольно часто ими являются занимательные задачи благодаря их важной особенности: трудность этих задач можно варьировать. Задания, составленные с помощью приемов занимательности («Зашифрованные задания», «Задания с продолжением», «Выбор», «Задумай» и т. д.), освобождены от той жесткости, фиксированности, запрограммированности, которая присуща многим учебным заданиям.

Действительно, учебное задание обычно заранее определяет основной ход решения. И для выполнения дидактических задач это очень важно. Однако наряду с ними в обучении надо использовать и задания, которые дают учащимся определенную свободу при их решении. Ведь это же есть не что иное, как творческий подход. Некоторые приемы занимательности («Выбор», «Соответствие», «Задумай» и др.) прекрасно этому способствуют.

Свобода при выполнении занимательных заданий важна и в методическом отношении. В некоторых случаях, например, появляется возможность подготавливать учащихся к формированию умений и навыков (часто на интуитивной основе). В других свобода помогает интуитивному освоению идей математики и приемов умственной работы.

Таким образом, приемы занимательности часто связаны с общими проблемами обучения: развитием приемов мышления, общеучебных умений и навыков и т.д. Значит, кроме прироста математических знаний, умений и навыков, математические задания часто выполняют и другие, не менее важные цели: развитие мышления и способностей ученика [8,с.52].

2.3 Методика использования занимательных заданий во внеурочное время

Самыми популярными видами учебного процесса на сегодняшний день являются внеклассные мероприятия. Их использование повышает интерес к учебе и знаниям, формируют сплоченный коллектив. Видов внеклассных мероприятий существуют довольно много. Самые распространенные из них представляют собой подражание многочисленным телевизионным играм, которые пришли к нам с голубых экранов: КВН, Звездный час, Своя игра, Брейн-ринг, Поле чудес, Слабое звено и т.д.

Рассмотрим некоторые из них. Математический КВН является собой распространенной формой внеклассной работы, которая интересна для учащихся всех возрастов. Как правило, КВН проводится во внеурочное время. Во время подготовки проведения КВНа следует щепетильно отнестись к организационному моменту, элементами которого является следующие пункты:

· Количественный состав команд, оформление команд;

· оформление помещения;

· счетная комиссия, ее состав, обязанности;

· состав жюри и порядок его работы;

· система оценок каждого конкурса;

· оформление итогов конкурса.

Игра «Звездный час», например, проводится в неделю математики, в рамках предметных недель в школе. Эта игра позволяет использовать выступления ребят, при этом учащиеся должны получить знания, умения и навыки по организации и поиску информации, которая нужна для представления данной темы. Применение новых информационных технологий дает возможность применять в обучении новые формы работы. Например, выполнение самостоятельно подготовленного доклада в форме презентаций повышает уровень заинтересованности учащихся. Использование элементов игры повышает мотивацию познавательной деятельности, внимательность учащихся к прослушиванию докладов и выступлений. Таким образом, проверяются и закрепляются полученные знания.

Игра «Счастливы случай» повышает уровень математического мышления, стимулирует углубление теоретических знаний, расширение кругозора, возникновение интереса к математике, воспитывает стремление к совершенствованию своих знаний, а также является способом организации свободного досуга учащихся. Эта игра во многом способствует формированию у учащихся умения коллективного поиска ответов на вопросы, помогает сплочению коллектива, формированию дружеских, товарищеских отношений, а также во время игры выявляются творческие и организаторские способности детей.

Игра «Слабое звено» вызывает у учащихся азарт, стремление к победе, способствует развитию логического мышления.

Интеллектуальная игра «Брейн-ринг» развивает познавательные и творческие способности у учащихся, логическое мышление, интуицию и внимание.

Игра «Поле чудес» носит развлекательный характер, и чаще всего ее проводят в канун какого-нибудь праздника. Массовость этой игры, многообразие и неожиданность заданий и сюрпризов способствует развитию интереса к математике и познавательных и творческих способностей учащихся.

«Своя игра» рассчитана на более узкий круг участников, и будет интересна, прежде всего, ученикам, посещающим факультативные занятия, и ребятам, проявляющим интерес к данной науке.

Учащиеся испытывают огромный интерес к занимательности, нередко многие из них проявляют творческую активность при составлении задач для викторин. Такую работу необходимо поощрять, только при этом условии учитель сможет вызвать интерес у учеников к такой непростой науке, как математике. Во внеклассных мероприятиях, где задействованы многие учащиеся, царит атмосфера соревнования, борьбы за лучшее составление задач.

Почти все формы занимательной математики являются массовыми средствами воспитательного воздействия на учащихся. Каждой из них свойственно свое построение и содержание, которые определяют возможность применения ее в конкретных условиях внеурочных занятий. Очень важно, что практически все формы занимательной математики несут в себе ту или иную степень игры. А, как нам известно, привить интерес, а может и любовь к сложному предмету, можно лишь через игру.[22, с. 110]

Заключение

В начале работы были представлены цель и основные задачи исследования, которые нашли свою реализацию в данной работе.

Были изучены источники психолого-педагогическая и методическая литература. Рассмотрены подходы к понятию «познавательный интерес», сущность и типология занимательных задач, приемы составления занимательных заданий. Также рассмотрена методика использования занимательных заданий на уроках и во внеурочное время, а также методика использования заданий, составленных с помощью приемов занимательности.

Таким образом, в ходе написания данной работы выполнены задачи, поставленные в начале исследования.

Итак, можно сделать вывод о том, что цель исследования достигнута.

Достоинство многих занимательных задач заключается в том, что при их решении у ученика часто возникает необходимость менять ход мысли на обратный. Умение менять ход мысли на обратный – ценнейшее качество ума. Занимательные задания способствуют формированию гибкости ума, освобождению мышления от шаблонов.

Занимательные задачи в настоящее время являются одним из основных средств формирования познавательного интереса к предмету и могут активно использоваться учителями на уроках математики.

Список литературы

1. Балаян Э.Н. 1001 олимпиадная и занимательная задача по математике. – Ростов-н/Д.: Феникс, 2008

2. Глейзер Г.И. История математики в школе.- М.: Просвещение, 1982

3. Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики.- М.: Мир, 1986

4. Давыдова М., Агапова И. Праздник в школе. – М.Айрис пресс, 2007

5. Дьюдени Г.Э. 520 головоломок. / Сост. и ред. амер. изд. М. Гарднер; пер. с англ. Ю.Н. Сударева. - 2-е изд., испр. – М. Мир, 2000

6. Егорченко И.В. Теория и методика использования реальности в обучении математике.-Саранск, 1999

7. Зенкевич И.Г. Эстетика урока математики: Пособие для учителя. - М.: Просвещение, 1981

8. Истомина Н.В. Методика обучения математике в начальных классах. – Ярославль: ЛИНКА ПРЕСС, 1997

9. Клейн Ф. Реформирование математического образования: история и современность. // Математика -2002. № 5.С.12-16

10. Кордемский Б.А. Математическая смекалка. — М.: ГИФМЛ, 2003

11. Кордемский Б.А. Математические завлекалки. - М: ОНИКС·АЛЬЯНС-В, 2000

12. Кордемский Б.А. Увлечь школьников математикой. (Материал для классных и внеклассных занятий). - М.: Просвещение, 1981

13. Курант Р., Роббинс Г. Что такое математика? - 4-е изд., стер. – М.: МЦНМО, 2007

14. Нестеренко Ю.В. Алгебра и теория чисел. – М.: Академия, 2008

15. Олехник С.Н., Нестеренко Ю.В. Старинные занимательные задачи. 2-е изд. – М.: Наука, 1988

16. Перельман Я.И. Занимательная алгебра. Веселые задачи. Простые, но каверзные. – М.: АСТ, 2007

17. Сендова Е. Действенная математика. // Математика в школе – 2004. № 3.С 9-11

18. Сухин И.Г. 800 новых логических и математических головоломок. – М.: АСТ, 2008

19. Творческие задачи для младших школьников: методическое пособие для студентов факультета педагогики и психологии развития ребенка. - Тула: Изд-во ТГПУ им. Л.Н. Толстого, 1996

20. Халамайзер А.Я. Математики смотрят в будущее. // Математика в школе – 1991. № 2. С 78-80.

21. Шевкин А.В Школьная математическая олимпиада. Задачи и решения. Выпуск 1. – М.: Илекса, 2008

22. Щербакова Ю.В. Занимательная математика на уроках и внеклассных мероприятиях.-М.: «Глобус», 2010.

23. Шуба М.Ю. Занимательные задания в обучении математике. – М.: Просвещение, 1994

24. http://www.mathedu.ru/about/

Приложение

1. Сценарий к мероприятию: «Час веселой математики»

Действующие лица: ведущий, Царь, изобретатель шахмат Сета, Придворный.

Ведущий.Сегодня мы хотим познакомить всех присутствующих с тем, какой интересный с математической точки зрения случай произошел в Древней Индии с изобретателем шахмат.

Шахматы – одна из самых древних игр. Она существует уже многие века, неудивительно, что с нею связаны предания, правдивость которых, за давностью лет, невозможно проверить. Одну из подобных легенд вы сейчас услышите.Чтобы понять ее, вовсе не обязательно уметь играть в шахматы. Достаточно знать, что игра происходит на доске, разграфленной на 64 клетки, и что эти клетки попеременно белые и черные. Итак, повторяю, что шахматная игра была придумана в Индии изобретателем по имени Сета.

Выходит Сета, одетый в покрывало, шаровары и чалму. Он складывает руки на груди и делает восточный поклон.

Когда индийский царь Шерам познакомился с шахматами, он был восхищен остроумием этой игры и разнообразием возможных ходов.

Выходит Царь, одетый так же, но побогаче. Возле него сгибается в поклоне Придворный.

Царь. Я восхищен этой новой игрой – шахматами. Кто ее изобретатель?

Придворный. Один из ваших подданных, о великий Царь. Его зовут Сета. Вот он.

Царь. Пусть Сета приблизится.

Сета подходит.

Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал.

Сета. Я счастлив, великий Царь, что сумел обрадовать тебя. (Кланяется)

Царь. Я достаточно богат, чтобы исполнить самое смелое твое пожелание. Назови награду, которая тебя удовлетворит, и ты получишь ее. Не робей, выскажи свою просьбу. Я не пожалею ничего, чтобы выполнить ее.

Сета. Велика доброта твоя, о повелитель. Но я так робею…Боюсь, мое желание покажется слишком дерзким.

Царь. Я дал обещание и выполню его. Говори!

Сета. Повелитель, прикажи мне выдать за первую клетку шахматной доски одно пшеничное зерно.

Царь. Простое пшеничное пшено?

Сета. Да, повелитель. За вторую клетку прикажи выдать два зерна, за третью – четыре, за четвертую – восемь, за пятую – 16, за шестую – 32.

Царь. Я понял, ты хочешь получить награду зернами пшеницы. Так, чтобы число зерен удваивалось за каждую клетку? И это все?

Сета. Да, повелитель.

Царь. Довольно. Ты получишь свои зерна за все 64 клетки доски согласно твоему желанию: за каждую вдвое больше, чем за предыдущую. Но знай, что твоя просьба недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, ты бы мог высказывать больше уважения к доброте твоего государя. Ступай, мои слуги вынесут тебе твой мешок с пшеницей.

Сета кланяется, улыбается и уходит.

Придворный! Пусть немедленно сосчитают, какова величина награды, потребованной этим изобретателем, и выдадут ему мешок.

Придворный уходит. Выходит слуга с опахалом в руках и начинает обмахивать Царя.

Ведущий. За обедом Царь вспомнил об изобретателе шахмат и пожелал узнать, унес ли тот свою жалкую награду.

Царь. Придворный! Подсчитан ли размер награды для сеты?

Придворный (входит).Повелитель, приказание твое исполняется. Придворные математики исчисляют число следуемых Сете зерен.

Царь. Почему мое приказание до сих пор не выполнено? Я не привык, чтобы мои приказания исполнялись так медленно!

Ведущий. Вечером, отправляясь ко сну, Царь еще раз осведомился, подсчитан ли размер награды для Сеты.

Царь. Придворный! Давно ли Сета со своим мешком пшеницы покинул дворей?

Придворный. Повелитель, математики твои трудятся без устали и надеются, что еще до рассвета закончат подсчет.

Царь. Почему медлят с этим делом? Завтра, прежде чем я проснусь, все до последнего зерна должно быть выдано Сете!

Ведущий. Рано утром к Царю явились с докладом.

Входит Придворный с большим свитком в руках.

Царь. Прежде чем ты скажешь о своем деле, я желаю услышать, выдана ли наконец Сете та награда, которую он себе назначил?

Придворный. Ради этого я и осмелился явиться перед тобой в столь ранний час. Мы добросовестно исчислили количество зерен, которое желает получить Сета. Число это так велико…

Царь. Как бы ни было оно велико, житницы мои не оскудеют. Награда обещана и должна быть выдана.

Придворный. Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве земли. Но если ты желаешь выдать обещанную награду, то прикажи осушить моря и океаны, превратить земные царства в пахотные поля, прикажи растопить льды и снега, покрывающие далекие северные пустыни. Пусть все это пространство будет сплошь засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду.

Царь. Назови же мне это чудовищное число1

Придворный. 18 квинтиллионов 446 квадриллионов 744 триллиона 73 биллиона 709 миллионов 551 тысяча 615, о повелитель! (Кланяется)

Царь в ужасе замирает, потом они уходят.

Ведущий. Вот это награда! Конечно, она не могла быть выдана, ведь только амбар для хранения такого гигантского количества зерна должен простираться на расстояние, вдвое большее, чем расстояние от Земли до Солнца. Да, индийский царь не в состоянии выдать подобной награды. Но все же есть вариант, как он мог бы освободиться от такого огромного долга.Кто из присутствующих может придумать выход для того, чтобы Царь мог избежать несчастной доли выдачи награды изобретателю шахмат?

(для этого нужно было предложить Сете самому отсчитать зерно за зерном всю причитавшуюся ему пшеницу) [4].

2. Тема урока: «Площадь. Формула площади прямоугольника»

Цели: формирование умений находить площадь прямоугольника и площадь квадрата по формулам

Ход урока:

1.Организационный.момент.

2.Подготовка к новой теме. Полезная сказка «Родственники» (сценка).

Жила на свете важная фигура. Важность ее признавалась всеми людьми, так как при изготовлении многих вещей форма ее служила образцом. А имела фигура такой вид:

Кого бы ни встретила она на своем пути, всем хвалилась:

-Посмотрите, какой у меня красивый вид: стороны мои все равные, углы все прямые. Если перегнусь я по средней вертикальной линии, то противоположные стороны мои так и сольются и углы один на другой точь-в-точь наложатся. Коли перегнусь я по средней горизонтальной линии, опять углы мои и противоположные стороны сравняются. Захочу перегнутся по любой линии, идущей с угла на угол, тогда и соседние стороны сольются. Красивее меня нет фигуры на свете!

- Как же зовут тебя, брат?- спрашивали встречные.

- А зовут меня просто…(назовите эту фигуру)

Ходил Квадрат по свету…И стало тяготить его одиночество: ни побеседовать задушевно не с кем, ни потрудиться в хорошей и дружной компании не приходится. А уж какое веселье одному! Весело бывает только вместе с друзьями. И решил Квадрат поискать родственников.

- Ежели встречу родственника, то я его сразу узнаю,- думал Квадрат,- ведь он на меня должен быть чем-то похож.

Однажды встречает он на пути такую фигуру:

Стал Квадрат к ней приглядываться. Что-то знакомое, родное увидел он в этой фигуре.

И спросил он тогда:

- Как зовут тебя, приятель?

- Называют меня…(Как называется эта фигура?)

- А мы не родственники ли с тобой?- продолжал спрашивать Квадрат.

- Я бы тоже был рад узнать об этом. Если у нас найдутся четыре признака, по которым мы похожи, то, значит, мы с тобой родственники и у нас тогда имеется общее название, - ответил Прямоугольник.

Стали они искать и нашли эти четыре признака сходства.

(Какие четыре признака сходства имеют квадрат и прямоугольник? Какое общее название они имеют?)

Обрадовались фигуры тому, что нашли друг друга.

Стали теперь они вдвоем жить-поживать, вместе трудиться, вместе веселиться, вместе по белу свету шагать.

Отдыхают они однажды на опушке леса и видят: выходит из-за кустарника какая-то новая фигура и направляется прямо к ним. А вид она имела такой:

Поздоровалась вежливо фигура с Квадратом и Прямоугольником и с облегчением говорит:

- Долго я искал представителей нашего старинного рода. Наконец-то я вас нашел, разыскал своих родственников.

-А как же тебя зовут?- с удивлением спросили новую фигуру.

- Зовут меня…(Как называют эту фигуру?)

- А как ты докажешь, что мы родственники?-вновь последовал вопрос.

- Очень просто. Мы все имеем два общих признака.

И эти два признака сходства были названы.(Назовите два признака, по которым эти фигуры имеют сходство.)

Так встретились и стали вместе жить три родственные фигуры, которые назывались теперь одним словом…(Каким одним словом называют эти фигуры?)

3.Изучение нового материала.

4.Закрепление.

5.Итог урока.

6.Домашнее задание.