Сферический треугольник и его применение.
Сферический треугольник
— геометрическая фигура на поверхности сферы, образованная пересечением трёх больших кругов. Три больших круга на поверхности сферы, не пересекающихся в одной точке, образуют восемь сферических треугольников. Сферический треугольник, все стороны которого меньше половины большого круга, называется эйлеровым.
Сторона сферического треугольника измеряется величиной опирающегося на неё центрального угла. Угол сферического треугольника измеряется величиной двугранного угла между плоскостями, в которых лежат стороны этого угла. Соотношения между элементами сферических треугольников изучает сферическая тригонометрия.
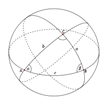
Свойства сферического треугольника:
- Помимо трёх признаков равенства плоских треугольников, для сферических треугольников верен ещё один: два сферических треугольника равны, если их соответствующие углы равны.
- Для сторон сферического треугольника выполняются 3 неравенства треугольника: каждая сторона меньше суммы двух других сторон и больше их разности.
- Сумма всех сторон a + b + c всегда меньше 2πR.
- Величина 2πR − (a + b + c) называется сферическим дефектом
- Сумма углов сферического треугольника s = α + β + γ всегда меньше 3π и больше π
- Величина называется сферическим избытком или сферическим эксцессом
- Площадь сферического треугольника определяется по формуле .
- В отличие от плоского треугольника, у сферического треугольника может быть два, и даже три угла по 90° каждый.
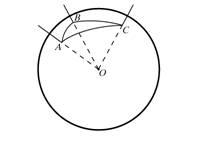
Среди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Три больших окружности, пересекаясь попарно в двух точках, образуют на сфере восемь сферических треугольников. Зная элементы (стороны и углы) одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами одного из них, того, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла ОАВС, углы треугольника – двугранными углами того же трехгранного угла см на рис.
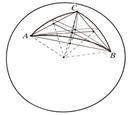 Свойства сферических треугольников во многом отличаются от свойств треугольников на плоскости. Так, к известным трем случаям равенства прямолинейных треугольников добавляется еще и четвертый: два треугольника АВС и А`В`С` равны, если равны соответственно три угла РА = РА`, РВ = РВ`, РС = РС`. Таким образом, на сфере не существует подобных треугольников, более того, в сферической геометрии нет самого понятия подобия, т.к. не существует преобразований, изменяющих все расстояния в одинаковое (не равное 1) число раз. Эти особенности связаны с нарушением евклидовой аксиомы о параллельных прямых и также присущи геометрии Лобачевского. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричными, таковы, например, треугольники АС`С и ВСС` Свойства сферических треугольников во многом отличаются от свойств треугольников на плоскости. Так, к известным трем случаям равенства прямолинейных треугольников добавляется еще и четвертый: два треугольника АВС и А`В`С` равны, если равны соответственно три угла РА = РА`, РВ = РВ`, РС = РС`. Таким образом, на сфере не существует подобных треугольников, более того, в сферической геометрии нет самого понятия подобия, т.к. не существует преобразований, изменяющих все расстояния в одинаковое (не равное 1) число раз. Эти особенности связаны с нарушением евклидовой аксиомы о параллельных прямых и также присущи геометрии Лобачевского. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричными, таковы, например, треугольники АС`С и ВСС`
Сумма углов всякого сферического треугольника всегда больше 180°. Разность РА+РВ +РС – p = d (измеряемая в радианах) – величина положительная и называется сферическим избытком данного сферического треугольника. Площадь сферического треугольника: S = R2 d где R – радиус сферы, а d – сферический избыток. Эта формула впервые была опубликована голландцем А.Жираром в 1629 и названа его именем.
Реклама

Если рассматривать двуугольник с углом a, то при 226 = 2p/n (n – целое число) сферу можно разрезать ровно на п копий такого двуугольника, а площадь сферы равна 4пR2 = 4p при R = 1, поэтому площадь двуугольника равна 4p/n = 2a. Эта формула верна и при a = 2pт/п и, следовательно, верна для всех a. Если продолжить стороны сферического треугольника АВС и выразить площадь сферы через площади образующихся при этом двуугольников с углами А, В, С и его собственную площадь, то можно прийти к вышеприведенной формуле Жирара.
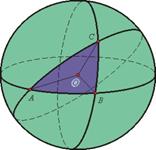 Под сферическим треугольником подразумевается треугольник на поверхности сферы, составленный из дуг больших кругов – т. е. таких окружностей, центром которых является центр сферы. Углы сферического треугольника – это углы между касательными к его сторонам, проведенными в его вершинах. Как и углы обычного треугольника, они меняются от 0 до 180°. В отличие от плоского треугольника, у сферического сумма углов не равна 180°, а больше: в этом нетрудно убедиться, рассмотрев, например, треугольник, образованный дугами двух меридианов и экватора на глобусе: хотя меридианы сходятся в полюсе, оба они перпендикулярны экватору, а значит, у этого треугольника два прямых угла! Под сферическим треугольником подразумевается треугольник на поверхности сферы, составленный из дуг больших кругов – т. е. таких окружностей, центром которых является центр сферы. Углы сферического треугольника – это углы между касательными к его сторонам, проведенными в его вершинах. Как и углы обычного треугольника, они меняются от 0 до 180°. В отличие от плоского треугольника, у сферического сумма углов не равна 180°, а больше: в этом нетрудно убедиться, рассмотрев, например, треугольник, образованный дугами двух меридианов и экватора на глобусе: хотя меридианы сходятся в полюсе, оба они перпендикулярны экватору, а значит, у этого треугольника два прямых угла!
У сферического треугольника может быть два прямых угла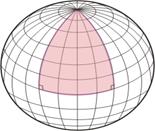
Уже у индийца Варахамихиры (V–VI вв.), у арабских математиков и астрономов начиная с IX в. (Сабит ибн Корра, ал-Баттани), а у западных математиков начиная с Региомонтана (XV в.) встречается в различных формулировках замечательная теорема о сферических треугольниках. Вот как она может быть сформулирована в современных обозначениях:
cosa = cosbcosc + sinbsinccosA. Сферическая теорема косинусов очень важна и для астрономии, и для географии. Эта теорема позволяет по координатам двух городов A и B находить расстояние между ними. Кроме того, математикам стран ислама сферическая теорема косинусов помогала в решении другой практической задачи: в городе с данными координатами находить направление на священный город Мекку (всякий правоверный мусульманин должен пять раз день молится в направлении Мекки). При решении этой задачи, считая город B Меккой, требовалось найти угол A того же треугольника.
Реклама

 Страница из «Собрания правил науки астрономии», XI в., автор неизвестен. Страница из «Собрания правил науки астрономии», XI в., автор неизвестен.
В астрономии сферическая теорема косинусов позволяет переходить из одной системы координат на небесной сфере в другую. Чаще всего используются три такие системы: у одной экватором служит небесный экватор, а полюсами – полюсы мира, вокруг которых происходит видимое суточное вращение светил; у другой экватором является эклиптика – круг, по которому в течение года совершается видимое движение Солнца на фоне звезд; у третьей роль экватора выполняет горизонт, а роль полюсов – зенит и надир. В частности, благодаря сферической теореме косинусов можно вычислять высоту Солнца над горизонтом в разные моменты времени и в разные дни в году.
Паруса в архитектуре — сферический треугольник, обеспечивающий переход от квадратного в плане подкупольного пространства к окружности купола. Па́рус, пандати́в (от фр. pendentif) — часть свода, элемент купольной конструкции, посредством которого осуществляется переход от прямоугольного основания к купольному перекрытию или его барабану. Парус имеет форму сферического треугольника, вершиной опущенной вниз, и заполняет пространство между подпружными арками, соединяющими соседние столпы подкупольного квадрата. Основания сферических треугольников парусов в сумме образуют окружность и распределяют нагрузку купола по периметру арок.
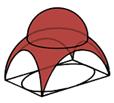 Купол на парусах Купол на парусах
 Роспись паруса Роспись паруса 
ДжорджНельсон (George Nelson)
May 23rd, 2010
"Дизайнер может несколько расслабиться и развлечься; в результате может возникнуть шутка, забава. Удивительно, как часто это бывает очень значительная забава" Джордж Нельсон
Джордж Нельсон – американский дизайнер, архитектор, критик и теоретик дизайна. (1908, Хартфорд, Коннектикут – 1986, Нью-Йорк)
Проектировал осветительную арматуру, часы, мебель, упаковку, занимался выставочным дизайном.
Наиболее известные дизайн проекты Джорджа Нельсона представляют собой виртуозную стилизацию геометрических форм в духе оп-арта или геометрического абстракционизма.
Форму своего знаменитого черного стула дизайнер строит на основе сферического треугольника, широко использовавшегося в архитектурных конструкциях купольных сооружений. В частности в византийских и русских храмах такой сферический треугольник назывался «парус». Благодаря «парусу» осуществлялся плавный переход от подкупольной опоры к куполу.
  ДжорджНельсон (George Harold Nelson, 1908—1986 гг.) ДжорджНельсон (George Harold Nelson, 1908—1986 гг.)
гравюра Эшера
 Концентрические сферы.1935г.Торцовая гравюра 24 на 24 см. Концентрические сферы.1935г.Торцовая гравюра 24 на 24 см.
Четыре полые концентрические сферы освещены центральным источником света. Каждая сфера состоит из сетки, образованной девятью большими пересекающимися кольцами; они членят сферическую поверхность на 48 подобных сферических треугольников. Ма́уриц Корне́лис Э́шер (нидерл. Maurits Cornelis 17 июня 1898, Леуварден, Нидерланды — 27 марта 1972, Ларен, Нидерланды) — нидерландский художник-график.

Применение сферического треугольника:
- Использование в трехмерной графике сферических треугольников
- В астрономии
- В географии. Теорема сферического треугольника позволяет по координатам двух городов A и B находить расстояние между ними.
- В архитектруе
- В дизайне в виде стула от Джорджа Нельсона
- В гравюре
|