ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Кафедра статистики
Экономический факультет
Контрольная работа
по дисциплине: Эконометрика
Вариант №3
Выполнила студентка III курса 33 группы
Специальность: «Финансы и кредит»
заочная форма обучения сокращ.прогр.
Проверила: доц.
Москва 2009
Содержание
Задача 1.3
Задача 2.11
Задача 3.12
Список литературы.. 16
По данным за два года изучаетсязависимость оборота розничной торговли (Y, млрд. руб.) от ряда факторов: X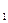 - денежные доходы населения, млрд. руб.; Х - денежные доходы населения, млрд. руб.; Х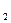 - доля доходов, используемая на покупку товаров и оплату услуг, млрд. руб.; Х - доля доходов, используемая на покупку товаров и оплату услуг, млрд. руб.; Х - численность безработных, млн. чел.; Х - численность безработных, млн. чел.; Х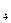 - официальный курс рубля по отношению к доллару США. - официальный курс рубля по отношению к доллару США.
Таблица №1
| Месяц |
Y |
X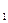 |
Х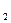 |
Х |
Х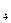 |
| 1 |
72,9 |
117,7 |
81,6 |
8,3 |
6,026 |
| 2 |
67,0 |
123,8 |
73,2 |
8,4 |
6,072 |
| 3 |
69,7 |
126,9 |
75,3 |
8,5 |
6,106 |
| 4 |
70,0 |
134,1 |
71,3 |
8,5 |
6,133 |
| 5 |
69,8 |
123,1 |
77,3 |
8,3 |
6,164 |
| 6 |
69,1 |
126,7 |
76,0 |
8,1 |
6,198 |
| 7 |
70,7 |
130,4 |
76,6 |
8,1 |
6,238 |
| 8 |
80,1 |
129,3 |
84,7 |
8,3 |
7,905 |
| 9 |
105,2 |
145,4 |
92,4 |
8,6 |
16,065 |
| 10 |
102,5 |
163,8 |
80,3 |
8,9 |
16,010 |
| 11 |
108,7 |
164,8 |
82,6 |
9,4 |
17,880 |
| 12 |
134,8 |
227,2 |
70,9 |
9,7 |
20,650 |
| 13 |
116,7 |
164,0 |
89,9 |
10,1 |
22,600 |
| 14 |
117,8 |
183,7 |
81,3 |
10,4 |
22,860 |
| 15 |
128,7 |
195,8 |
83,7 |
10,0 |
24,180 |
| 16 |
129,8 |
219,4 |
76,1 |
9,6 |
24,230 |
| 17 |
133,1 |
209,8 |
80,4 |
9,1 |
24,440 |
| 18 |
136,3 |
223,3 |
78,1 |
8,8 |
24,220 |
| 19 |
139,7 |
223,6 |
79,8 |
8,7 |
24,190 |
| 20 |
151,0 |
236,6 |
82,1 |
8,6 |
24,750 |
| 21 |
154,6 |
236,6 |
83,2 |
8,7 |
25,080 |
| 22 |
160,2 |
248,6 |
80,8 |
8,9 |
26,050 |
| 23 |
163,2 |
253,4 |
81,8 |
9,1 |
26,420 |
| 24 |
191,7 |
351,4 |
68,3 |
9,1 |
27,000 |
Задание:
1. Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии.
2. Выделите значимые и незначимые факторы в модели. Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели.
3. Для полученной модели проверьте выполнение условия гомоскедастичности остатков, применив тест Голдфельда-Квандта.
4. Проверьте полученную модель на наличие автокорреляции остатков с помощью теста Дарвина-Уотсона
5. Проверьте, адекватно ли предположение об однородности исходных данных в регрессивном смысле. Можно ли объединить выборки (по первым 12 и остальным наблюдениям) в одну и рассматривать единую модель регрессии Y по Х?
Решение:
1. Для заданного набора данных построим линейную модель множественной регрессии.
Yх
= а + b1
Х1
+ b2
Х2
+ b3
Х3
+ b4
Х4
+ e
Таблица №2
| Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
| Y-пересечение |
-63,12339216 |
24,03915584 |
-2,625857272 |
0,016639889 |
-113,4379235 |
-12,80886085 |
| X1 |
0,495117715 |
0,036188344 |
13,68169026 |
2,74417E-11 |
0,41937464 |
0,570860789 |
| X2 |
0,983476231 |
0,175264351 |
5,611387733 |
2,06783E-05 |
0,616643729 |
1,350308734 |
| X3 |
-1,307234046 |
1,445807723 |
-0,904154837 |
0,377235119 |
-4,333344382 |
1,71887629 |
| X4 |
1,087907312 |
0,291987593 |
3,725868289 |
0,001432703 |
0,476770258 |
1,699044365 |
Параметры модели рассчитаем методом наименьших квадратов:
а = - 63,12, b1
= 0,5, b2
= 0,98, b3
= -1,31 и b4
= 1,09
Уравнение множественной регрессии имеет вид:
Yх
= - 63,12 + 0,5Х1
+ 0,98Х2
– 1,31Х3
+ 1,09Х4
+ e
Оценим точность полученной модели. Вычислим парные коэффициенты корреляции используя формулу:
ryxi
=

Сводные результаты корреляционного анализа представим в таблице:
Таблица №3
| Y |
X1
|
X2
|
X3
|
X4
|
Y
X1
X2
X3
X4
|
1
0,967
0,048
0,469
0,947
|
1
- 0,191
0,384
0,862
|
1
0,184
0,209
|
1
0,646
|
1
|
Для оценки адекватности построенного уравнения регрессии заполним следующую таблицу:
Реклама

Таблица №4
| Регрессионная статистика
|
| Множественный R |
0,997719294 |
| R-квадрат |
0,99544379 |
| Нормированный R-квадрат |
0,994484588 |
| Стандартная ошибка |
2,729949461 |
| Наблюдения |
24 |
Коэффициент множественной корреляции показывает, что факторы Х1
, Х2
, Х3
, Х4
, объясняют вариацию признака Y на 99,8%, а необъясненные факторы 0,2%.
С помощью t-критерия Стьюдента оценим значимость коэффициентов уравнения регрессии а, b1
, b2
, b3
и b4
:
Таблица №5
| Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
| Y-пересечение |
-63,12339216 |
24,03915584 |
-2,625857272 |
0,016639889 |
| X1 |
0,495117715 |
0,036188344 |
13,68169026 |
2,74417E-11 |
| X2 |
0,983476231 |
0,175264351 |
5,611387733 |
2,06783E-05 |
| X3 |
-1,307234046 |
1,445807723 |
-0,904154837 |
0,377235119 |
| X4 |
1,087907312 |
0,291987593 |
3,725868289 |
0,001432703 |
Табличное значение t - критерия при 5% уровне значимости и степенях свободы (24 – 4 – 1 = 19) составляет 2,09, условие 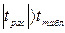 выполняется для коэффициентов b1
, b2
и b4
, значит они существенны (значимы), соответственно коэффициент b3
не значим. выполняется для коэффициентов b1
, b2
и b4
, значит они существенны (значимы), соответственно коэффициент b3
не значим.
На основе вычисления F-критерия Фишера произведем проверку значимости полученного уравнения регрессии с вероятностью 0,95:
F = 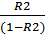 * * 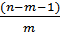
F = 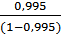 * *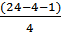 = 945 = 945
получили F>Fтабл
= 2,90 для a = 0,05; m1
= m = 4, m2
= n – m – 1 = 19.
Поскольку Fрас
>Fтабл
, уравнение множественной регрессии следует признать адекватным.
2. Исключим несущественные факторы Х3
и построим уравнение зависимости 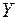 (балансовой прибыли) от объясняющих переменных Х1
, Х2
, и Х4
.
(балансовой прибыли) от объясняющих переменных Х1
, Х2
, и Х4
.
Построим уравнение регрессии со статистически значимыми факторами.
Y = a + b1
X1
+ b2
X2
+ b4
X4
+ e
Методом наименьших квадратов найдем параметры модели:
а = - 80,81, b1
= 0,51, b2
= 1,06, b4
= 0,90
Следовательно, уравнение регрессии имеет вид:
Yх
= - 80,81 + 0,51Х1
+ 1,06Х2
+ 0,90Х4
+ e
Таблица № 6
| Регрессионная статистика
|
| Множественный R |
0,997621047 |
| R-квадрат |
0,995247754 |
| Нормированный R-квадрат |
0,994534917 |
| Стандартная ошибка |
2,717465246 |
| Наблюдения |
24 |
| Дисперсионный анализ |
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия |
3 |
30930,73724 |
10310,24575 |
1396,178737 |
2,16904E-23 |
| Остаток |
20 |
147,6923473 |
7,384617364 |
| Итого |
23 |
31078,42958 |
| Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
| Y-пересечение |
-80,80788211 |
13,91182082 |
-5,808576977 |
1,10503E-05 |
-109,827432 |
-51,78833248 |
| X1 |
0,514732775 |
0,028832194 |
17,85270937 |
9,33007E-14 |
0,454589873 |
0,574875677 |
| X2 |
1,055202046 |
0,155568647 |
6,782870859 |
1,35061E-06 |
0,730691534 |
1,379712557 |
| X4 |
0,896552042 |
0,200239952 |
4,477388412 |
0,000230607 |
0,478858822 |
1,314245261 |
Оценим точность и адекватность полученной модели.
Коэффициент детерминации: R2
= 0,995.
Коэффициент корреляции: rху
= 0,997.
Остаточная сумма квадратов: С = 147,69
На основе вычисления F-критерия Фишера произведем проверку значимости полученного уравнения регрессии с вероятностью 0,95:
F = 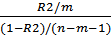
F = 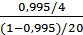 = 945 = 945
получили F>Fтабл
= 3,10 для a = 0,05; m1
= m = 3, m2
= n – m – 1 = 20.
Поскольку Fрас
>Fтабл
, уравнение множественной регрессии следует признать значимым.
Экономическая интерпретация параметров модели.
b1
= 0,51, значит при увеличении только денежных доходов населения на 1 млрд. руб. объем оборота розничной торговли в среднем вырастет на 0,51 млрд. руб.
b2
= 1,06, значит при увеличении только доли доходов, используемых на покупку товаров и услуг, на 1 млрд. руб. объем оборота розничной торговли в среднем вырастет на 1,06 млрд. руб.
b4
= 0,9, значит при увеличении только официального курса рубля по отношению к доллару на 1 руб. объем оборота розничной торговли в среднем вырастет на 0,9 млрд. руб.
Рассчитаем частные коэффициенты эластичности:
_
Х1
185,81
Э1
= b1
—
= 0,51 * ———— = 0,83
Реклама

Y 114,3
_
Х2
79,49
Э2
= b2
—
= 1,06 * ——— = 0,74
Y 114,3
_
Х4
17,39
Э4
= b4
—
= 0,9 * ——— = 0,14
Y 114,3
Они показывают, на сколько процентов изменяется зависимая переменная Y при изменении фактора Хi
на один процент.
3. Применим тест Голдфельда-Квандта для проверки гомоскедастичности остатков в полученной модели.
Упорядочим наблюдения в порядке возрастания переменной Х1
и, исключив из рассмотрения 6 центральных наблюдения, разделим совокупность из оставшихся 18 наблюдений на две группы (соответственно с малыми и большими значениями фактора Х1
). Определим по каждой из групп уравнение регрессии и остаточной суммы квадратов.
Проверка линейной регрессии на гомоскедастичность.
Таблица № 7
| Уравнения регрессии |
Х1
|
Х2
|
Х4
|
Y |
Ŷ |
E |
E2
|
Первая группа с первыми 9 месяцами
Y = -23,13 + 0,23Х1
- 0,69Х2
+ 1,97Х4
r = 0,997
F = 318,9
|
117,7 |
81,6 |
6,026 |
72,9 |
71,69 |
1,21 |
1,4748 |
| 123,1 |
77,3 |
6,164 |
69,8 |
70,22 |
-0,42 |
0,1800 |
| 123,8 |
73,2 |
6,072 |
67 |
67,38 |
-0,38 |
0,1438 |
| 126,7 |
76 |
6,198 |
69,1 |
70,21 |
-1,11 |
1,2432 |
| 126,9 |
75,3 |
6,106 |
69,7 |
69,60 |
0,10 |
0,0105 |
| 129,3 |
84,7 |
7,905 |
80,1 |
80,15 |
-0,05 |
0,0029 |
| 130,4 |
76,6 |
6,238 |
70,7 |
71,55 |
-0,85 |
0,7202 |
| 134,1 |
71,3 |
6,133 |
70 |
68,53 |
1,47 |
2,1486 |
| 145,4 |
92,4 |
16,065 |
105,2 |
105,16 |
0,04 |
0,0015 |
| Сумма |
5,93 |
Вторая группа с последними 9 месяцами
Y = - 122,45 + 0,64Х1
+ 2,17Х2
– 2,17Х4
r = 0,991
F = 97,5
|
219,4 |
76,1 |
24,23 |
129,8 |
130,90 |
-1,10 |
1,2003 |
| 223,3 |
78,1 |
24,22 |
136,3 |
137,76 |
-1,46 |
2,1253 |
| 223,6 |
79,8 |
24,19 |
139,7 |
141,70 |
-2,00 |
3,9894 |
| 227,2 |
70,9 |
20,65 |
134,8 |
132,43 |
2,37 |
5,6191 |
| 236,6 |
82,1 |
24,75 |
151 |
153,83 |
-2,83 |
7,9921 |
| 236,6 |
83,2 |
25,08 |
154,6 |
155,49 |
-0,89 |
0,7963 |
| 248,6 |
80,8 |
26,05 |
160,2 |
155,91 |
4,29 |
18,4012 |
| 253,4 |
81,8 |
26,42 |
163,2 |
160,36 |
2,84 |
8,0601 |
| 351,4 |
68,3 |
27 |
191,7 |
192,93 |
-1,23 |
1,5104 |
| Сумма |
49,69 |
Получаем R = 49,69 / 5,93 = 8,38, т.к. R больше табличного значения F-критерия 5,05 при 5%-ном уровне значимости для числа степеней свободы 5 для каждой остаточной суммы квадратов ((24 – 6 – 4*2) / 2), то условие Голдфельда-Квандта не выполняется, т.е. не подтверждается гомоскедастичность остатков.
4. Проверим полученную модель на наличие автокорреляции остатков помощью теста Дарбина-Уотсона.
Построим вспомогательную таблицу:
Таблица №8
| ei
|
ei-
1
|
(ei
- ei-1
)^2 |
(ei
)^2 |
| 1,790689805 |
3,20657 |
| 1,212351757 |
1,79069 |
0,334474898 |
1,469797 |
| 0,405921312 |
1,212352 |
0,650330062 |
0,164772 |
| 1,045605195 |
0,405921 |
0,40919547 |
1,09329 |
| 0,095870732 |
1,045605 |
0,901995551 |
0,009191 |
| -1,4064696 |
0,095871 |
2,257026466 |
1,978157 |
| -2,27200717 |
-1,40647 |
0,749155294 |
5,162017 |
| -1,84562984 |
-2,27201 |
0,18179763 |
3,40635 |
| -0,77494548 |
-1,84563 |
1,146365005 |
0,60054 |
| -0,23304391 |
-0,77495 |
0,293657307 |
0,054309 |
| 1,829073393 |
-0,23304 |
4,252327772 |
3,345509 |
| 5,919066869 |
1,829073 |
16,72804664 |
35,03535 |
| -1,1740676 |
5,919067 |
50,31255666 |
1,378435 |
| -1,26067668 |
-1,17407 |
0,007501132 |
1,589306 |
| -0,67087525 |
-1,26068 |
0,347865725 |
0,450074 |
| -4,35852294 |
-0,67088 |
13,59874549 |
18,99672 |
| -1,41641823 |
-4,35852 |
8,655980107 |
2,006241 |
| -2,79134265 |
-1,41642 |
1,89041716 |
7,791594 |
| -1,30987375 |
-2,79134 |
2,194750123 |
1,715769 |
| 0,551649133 |
-1,30987 |
3,465267431 |
0,304317 |
| 2,84153927 |
0,551649 |
5,243596841 |
8,074345 |
| 4,066646367 |
2,841539 |
1,500887399 |
16,53761 |
| 3,56552621 |
4,066646 |
0,251121412 |
12,71298 |
| -3,81006694 |
3,565526 |
54,39937426 |
14,51661 |
| СУММА
|
169,7724358
|
141,5999
|
При проверке независимости уровней ряда остатков определяется отсутствие в ряду остатков систематической составляющей. Это проверяется с помощью d – критерия Дарбина-Уотсона, в соответствии с которым вычисляется коэффициент d:
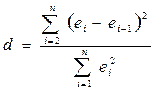 . .
d = 1,198959
По таблице критических точек распределения Дарбина–Уотсона для заданного уровня значимости 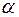 , числа наблюдений , числа наблюдений 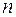 и количества объясняющих переменных m
определить два значения: d
н
- нижняя граница и d
в
- верхняя граница.
и количества объясняющих переменных m
определить два значения: d
н
- нижняя граница и d
в
- верхняя граница.
В нашем случае модель содержит 3 объясняющие переменные (m
=3), нижняя и верхняя границы равны соответственно d
н
= 1,10 и d
в
= 1,66.
Расчетное значение d-статистики лежит в интервале 0≤d≤d
н
. Следовательно, в ряду остатков существует положительная автокорреляция.
5. Проверим адекватность предположения об однородности исходных данных в регрессионном смысле. Можно ли объединить две выборки (по первым 12 и остальным наблюдениям) в одну и рассматривать единую модель регрессии Y по Х?
Для проверки предположения об однородности исходных данных в регрессионном смысле применим тест Чоу.
Разделим совокупность наблюдений на две группы: первые 12 наблюдений и последние 12 наблюдений. Определим по каждой из групп уравнение регрессии и остаточной суммы квадратов.
Таблица №9
| Уравнения регрессии |
Х1
|
Х2
|
Х4
|
Y |
Ŷ |
E |
E2
|
Первая группа с первыми 12 месяцами
Y = - 68,82+0,52Х1
+ 0,87Х2
- 1,08Х3
|
117,7 |
81,6 |
6,026 |
72,9 |
70,17 |
-2,73 |
7,4513 |
| 123,8 |
73,2 |
6,072 |
67 |
66,12 |
-0,88 |
0,7754 |
| 126,9 |
75,3 |
6,106 |
69,7 |
69,60 |
-0,10 |
0,0095 |
| 134,1 |
71,3 |
6,133 |
70 |
69,93 |
-0,07 |
0,0052 |
| 123,1 |
77,3 |
6,164 |
69,8 |
69,41 |
-0,39 |
0,1501 |
| 126,7 |
76 |
6,198 |
69,1 |
70,21 |
1,11 |
1,2213 |
| 130,4 |
76,6 |
6,238 |
70,7 |
72,71 |
2,01 |
4,0254 |
| 129,3 |
84,7 |
7,905 |
80,1 |
80,97 |
0,87 |
0,7499 |
| 145,4 |
92,4 |
16,065 |
105,2 |
104,90 |
-0,30 |
0,0892 |
| 163,8 |
80,3 |
16,01 |
102,5 |
103,97 |
1,47 |
2,1539 |
| 164,8 |
82,6 |
17,88 |
108,7 |
108,51 |
-0,19 |
0,0362 |
| 227,2 |
70,9 |
20,65 |
134,8 |
134,01 |
-0,79 |
0,6218 |
| Сумма |
17,29 |
Вторая группа с оставшимися 12 месяцами
Y = - 180,51+0,48Х1
+ 1,48Х2
+ 3,88Х3
|
164 |
89,9 |
22,6 |
116,7 |
118,64 |
1,94 |
3,7566 |
| 183,7 |
81,3 |
22,86 |
117,8 |
116,28 |
-1,52 |
2,3051 |
| 195,8 |
83,7 |
24,18 |
128,7 |
130,73 |
2,03 |
4,1131 |
| 219,4 |
76,1 |
24,23 |
129,8 |
130,90 |
1,10 |
1,2075 |
| 209,8 |
80,4 |
24,44 |
133,1 |
133,52 |
0,42 |
0,1723 |
| 223,3 |
78,1 |
24,22 |
136,3 |
135,68 |
-0,62 |
0,3783 |
| 223,6 |
79,8 |
24,19 |
139,7 |
138,23 |
-1,47 |
2,1529 |
| 236,6 |
82,1 |
24,75 |
151 |
150,01 |
-0,99 |
0,9765 |
| 236,6 |
83,2 |
25,08 |
154,6 |
152,92 |
-1,68 |
2,8117 |
| 248,6 |
80,8 |
26,05 |
160,2 |
158,85 |
-1,35 |
1,8343 |
| 253,4 |
81,8 |
26,42 |
163,2 |
164,05 |
0,85 |
0,7252 |
| 351,4 |
68,3 |
27 |
191,7 |
192,99 |
1,29 |
1,6589 |
| Сумма |
22,09 |
Таким образом, С1
= 17,29, С2
= 22,09.
Остаточная сумма квадратов по кусочно-линейной модели:
Скл
= С1
+ С2
= 17,29 + 22,09 = 39,38
Соответствующее ей число степеней свободы составит 16
Остаточная сумма квадратов единого уравнения тренда: С = 147,69
Сокращение остаточной дисперсии при переходе от единого уравнения к кусочно-линейной модели можно определить следующим образом:
ΔС = С – Скл
= 147,69 – 39,38 = 108,31
Далее в соответствии с предложенной Г. Чоу методикой определим фактическое значение F-критерия по следующим дисперсиям на одну степень свободы вариации:
Fрас
= 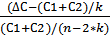 = = 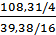 = 11,0 = 11,0
 Получили Fрас
> Fтабл
= 3,01 значит, гипотеза о структурной стабильности тенденции не принимается, а влияние структурных изменений на динамику Y признаем значимым. Получили Fрас
> Fтабл
= 3,01 значит, гипотеза о структурной стабильности тенденции не принимается, а влияние структурных изменений на динамику Y признаем значимым.
Модель макроэкономической производственной функции описывается следующим уравнением:
lnY
= -3,52 + 1,53lnK
+ 0,47lnL
+ ε , R
2
= 0,875.
(2,43) (0,55) (0,09) F = 237,4
В скобках указаны значения стандартных ошибок для коэффициентов регрессии.
Задание
:
1. Оцените значимость коэффициентов модели по t-критерию Стьюдента и сделайте вывод о целесообразности включения факторов в модель.
2. Запишите уравнение в степенной форме и дайте интерпретацию параметров.
3. Можно ли сказать, что прирост ВНП в большей степени связан с приростом затрат капитала, нежели с приростом затрат труда?
Решение:
1. Коэффициент детерминации 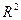 =0,875, показывает, что данная модель объясняет 87,5% вариацию ВНП, а необъясненные факторы – 12,5%. =0,875, показывает, что данная модель объясняет 87,5% вариацию ВНП, а необъясненные факторы – 12,5%.
Значимость коэффициентов модели b0
, b1
, b2
оценим с использованием t-критерия Стьюдента:
tb
0
= -3,52 / 2,43 = -1,45
tb
1
= 1,53 / 0,55 = 2,78
tb
2
= 0,47 / 0,09 = 5,22
Табличное значение t - критерия при 5% уровне значимости составляет 2,16. так как 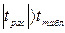 выполняется только для коэффициентов b1
и b2
, то коэффициенты модели b1
и b2
существенны (значимы). выполняется только для коэффициентов b1
и b2
, то коэффициенты модели b1
и b2
существенны (значимы).
Таким образом, целесообразно включение в модель обоих факторов (затраты капитала и затраты труда).
2. Запишем уравнение в степенной форме:
Y = е -3,52
* К1,53
* L0,47
* ε1
Интерпретация параметров:
b1
= 1,53, значит при увеличении только затрат капитала на 1% ВНП в среднем увеличится на 1,5% (1,011,53
= 1,015);
b2
= 0,47, значит при увеличении только затрат труда на 1% ВНП вырастет в среднем на 0,5% (1,01,47
= 1,005).
3. Прирост ВНП в большей степени связан с приростом затрат капитала, нежели с приростом затрат труда, это видно из интерпретации параметров.
Структурная форма модели имеет вид:
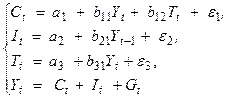
где: Ct
– совокупное потребление в период t
,
Yt
– совокупный доход в период t
,
It
– инвестиции в период t
,
Т
t
– налоги в период t
,
Gt
– государственные расходы в период t
,
Yt
-1
– совокупный доход в период t
-1
.
Задание:
1. Проверьте каждое уравнение модели на идентифицируемость, применив необходимое и достаточное условия идентифицируемости.
2. Запишите приведенную форму модели.
3. Определите метод оценки структурных параметров каждого уравнения.
Решение:
1 уравнения – функция потребления
2 уравнения – функция инвестиций
3 уравнения – функция налога
4 уравнения – тождество дохода
Модель представляет собой систему одновременных уравнений. Проверим каждое уравнения системы на необходимое и достаточное условия идентифицируемости.
В модели четыре эндогенные переменные (Сt
, It
, Tt
, Yt
) и две предопределенных переменных – одна экзогенная (Gt
) и одна лаговая (Yt
-1
). Последнее уравнение представляет собой тождество, поэтому практически статистическое решение необходимо только для первых трех уравнений системы, которые необходимо проверить на идентифицируемость.
1. Обозначим через Н число эндогенных переменных в уравнении системы и через D число экзогенных переменных, отсутствующих в уравнении системы.
1 уравнения
Сt
= а1
+ b11
Yt
+ b12
Tt
+ e1
В рассматриваемой эконометрической модели первое уравнение системы неидентифицируемо, ибо оно содержит Н = 3 и D = 2, и выполняется необходимое условие (D + 1 = Н), однако, не выполняется достаточное условие идентификации, ранг матрицы равен 2 < 3, что видно в следующей таблице:
| Уравнения |
It
|
Gt
|
Yt-1
|
| 2 |
-1 |
0 |
b21
|
| 3 |
0 |
0 |
0 |
| 4 |
1 |
1 |
0 |
2 уравнения
It
= а2
+ b21
Yt
-1
+ e2
Второе уравнение системы сверхидентифицируемо: Н = 1 и D = 1, т.е. счетное правило выполнено: D + 1 > Н, также выполнено достаточное условие идентификации: ранг матрицы 3 и определитель не равен 0:
| Уравнения |
Сt
|
Yt
|
Тt
|
Gt
|
| 1 |
-1 |
b21
|
b12
|
0 |
| 3 |
0 |
b31
|
- 1 |
0 |
| 4 |
1 |
0 |
0 |
1 |
3 уравнения
Tt
= а3
+ b31
Yt
+ e3
Третье уравнение системы также сверхидентифицируемо: Н = 2 и D = 2, т.е. счетное правило выполнено: D + 1 > Н, также выполнено достаточное условие идентификации: ранг матрицы 3 и определитель не равен 0:
| Уравнения |
Сt
|
It
|
Gt
|
Yt-1
|
| 1 |
-1 |
0 |
0 |
0 |
| 2 |
0 |
- 1 |
0 |
b21
|
| 4 |
1 |
1 |
1 |
0 |
Таким образом, структурная модель неидентифицируема, поскольку в системе имеются неидентифицируемые уравнения.
2. Запишем приведенную форму модели.
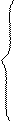 Сt
= δ1
+ δ11
Gt
+ δ12
Yt
-1
+ ζ1 Сt
= δ1
+ δ11
Gt
+ δ12
Yt
-1
+ ζ1
It
= δ2
+ δ21
Gt
+ δ22
Yt-1
+ ζ2
Tt
= δ3
+ δ31
Gt
+ δ32
Yt-1
+ ζ3
Yt
= δ4
+ δ41
Gt
+ δ42
Yt-1
+ ζ4
3. Метод оценки структурных параметров первого уравнения системы – метод максимального правдоподобия, а второго и третьего уравнений системы - двухшаговый метод наименьших квадратов.
1. «Практикум по эконометрике: Учебное пособие», И.И. Елисеева, С.В, Курышева, Н.М. Гордиенко и др.; под ред. И.И. Елисеевой, – М.: Финансы и статистика, 2005;
2. «Эконометрика: учебник», под ред. И.И. Елисеевой, - М.: «Финансы и статистика», 2008;
3. Магнус Я.Р., Катышев П.К., Пересецкий А.А., «Эконометрика: начальный курс», - М.: «Дело», 2004;
4. Орлова И.В., «Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL. Практикум: Учебное пособие для вузов», – М.: Финстатинформ, 2006.
«___»_________200_г. ____________________
(подпись студента)
|