| Нижегородский Государственный Технический Университет
Павловский филиал
Курсовая работа
по информатике на тему:
“Технология решения задач линейного программирования с помощью Поиска решений приложения
Excel”
.
Выполнила
: Бородулина Д.А.
Группа 05-АМ.
Проверила
: Ловыгина М.Б.
Павлово 2006 г.
Содержание
Введение……………………………………………………………………………стр.
3
Решение задач с помощью надстройки Поиск решения
- Установка программы Поиск решения…………………………………………..…стр.4
- Диалоговое окно Поиск решения…………………………………………………..…стр.4
- Ввод и редактирование ограничений………………………………………………..стр.5
- Настройка параметров алгоритма и программы……………………………….стр.6
Сохранение и загрузка модели
- Сохранение модели оптимизации…………………………………………………....стр.9
- Загрузка модели оптимизации……………………………………………………….стр.9
Вычисления и результаты решения задачи………………………………..стр.
10
Просмотр промежуточных результатов поиска решения…………...стр.11
Возникающие проблемы и сообщения процедуры поиска решения…...стр.12
Итоговые сообщения процедуры поиска решения……………………....стр.13
Примеры выполнения задач
- Пример № 1………………………………………………………………………………стр.15
- Пример № 2 (графическим способом)……………………………………………...стр..20
Вывод……………………………………………………………………………....стр.24
Список литературы…………………………………………………………....стр.25
Введение
Линейная оптимизация
– это раздел математического программирования, посвящённый нахождению экстремума линейных функций нескольких переменных при дополнительных линейных ограничениях, которые налагаются на переменные. Методы, с помощью которых решаются задачи, подразделяются на универсальные (например, симплексный метод) и специальные. С помощью универсальных методов решаются любые задачи линейного программирования. Особенностью задач линейного программирования является то, что экстремум целевой функции достигается на границе области допустимых решений.
Использование электронных таблиц широко распространено для решения многочисленных и разнообразных задач, связанных с учётом и контролем результатов управленческой деятельности: торгово-закупочных операций, производственных планов, бухучёта и т. п. Вместе с тем форма электронной таблицы оказывается очень удобной при решении многих аналитических задач управления деятельностью, и в частности задач исследования операций и поиска оптимальных решений.
В экономике оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования конкретного экономического объекта, когда возникает ситуация выбора варианта, наилучшего по некоторому правилу, критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции).
Такие задачи в Excel решают с помощью Поиска решения
.
Реклама

Процедура Поиск решения
представляет собой мощный инструмент для выполнения сложных вычислений. Она позволяет находить значения переменных, удовлетворяющих указанным критериям оптимальности, при условии выполнения заданных ограничений.
Решение задач с помощью надстройки Поиск решения
1. Установка программы Поиск решения
В меню Сервис
выберите команду Надстройки.
В диалоговом окне Надстройки
установите флажок Поиск решения.
Если диалоговое окно Надстройки
не содержит команды Поиск решения
, нажмите кнопку Обзор
и укажите диск и папку, в которой содержится файл надстройки Solver.
xla
(как правило, это папка Library\
Solver
folder) или запустите программу Setup
, если найти файл не удаётся.
Надстройка, указанная в диалоговом окне Надстройки
, остаётся активной до тех пор, пока она не будет удалена.
2. Диалоговое окно Поиск решения
Окно Поиск решения
(рис. 1) вызывается командой меню Сервис>Поиск решения.
Поле Установить целевую ячейку
служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу.

Рис.1.Диалоговое окно
Поиск решения.
Кнопка Равной
служит для выбора варианта с заданным значением целевой ячейки. Чтобы установить заданное число, введите его в поле.
Поле Изменяя ячейки
служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле Установить целевую
ячейку.
В поле Изменяя ячейки
вводятся имена или адреса изменяемых ячеек, разделяя их запятыми. Изменяемые ячейки должны быть прямо или косвенно связаны с целевой ячейкой. Допускается установка до 200
изменяемых ячеек.
Поле Предположить
используется для автоматического поиска ячеек, влияющих на формулу, ссылка на которую дана в поле Установить целевую
ячейку. Результат поиска отображается в поле Изменяя ячейки.
Поля Ограничения
служат для отображения списка граничных условий, налагаемые на переменные задачи. Допускаются ограничения в виде равенств, неравенств, а также – требование целочисленности переменных. Ограничения добавляются по одному с помощью кнопки Добавить.
Команда Изменить
служит для отображения диалогового окна Изменение ограничения.
Команда Удалить
служит для снятия указанного курсором ограничения.
Реклама

Команда Выполнить
служит для запуска поиска решения поставленной задачи.
Команда Закрыть
служит для выхода из окна диалога без запуска поиска решения поставленной задачи. При этом сохраняются установки, сделанные в окнах диалога, появлявшихся после нажатий на кнопки Параметры, Добавить, Изменить
или Удалить.
Кнопка Параметры
служит для отображения диалогового окна Параметры поиска решения
, в котором можно загрузить или сохранить оптимизируемую модель и указать предусмотренные варианты поиска решения.
Кнопка Восстановить
служит для очистки полей окна диалога и восстановления значений параметров поиска решения, используемых по умолчанию.
3.Ввод и редактирование ограничений
Диалоговые окна изменения и добавления ограничений одинаковы, рис.2.
В поле Ссылка на ячейку
вводится адрес или имя ячейки или диапазона, на значения которых накладываются ограничения.
Выберите из раскрывающегося списка условный оператор, который необходимо разместить между ссылкой и её ограничением. Это знаки операторов: не более, не менее, равно и т. д.
В поле Ограничения
введите число, формулу или имя ячейки или диапазона содержащих или вычисляющих ограничивающие значения.
Чтобы приступить к набору нового условия, нажмите кнопку Добавить.
Чтобы вернуться в диалоговое окно Поиск решения,
нажмите кнопку ОК.
Условные операторы целого и двоичного типа можно применять только при наложении ограничений на изменяемые ячейки.

Рис.2.Диалоговое окно
Изменение ограничения.
4. Настройка параметров алгоритма и программы
Настройка параметров алгоритма и программы производится в диалоговом окне Параметры поиска решения
, рис. 3.
В окне устанавливаются ограничения на время решения задач, выбираются алгоритмы, задаётся точность решения, предоставляется возможность для сохранения вариантов модели и их последующей загрузки. Значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач.
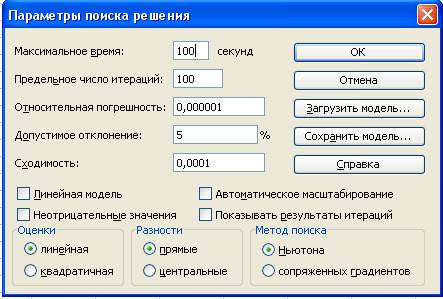
Рис. 3. Диалоговое окно
Параметры поиска решения.
Поле Максимальное время
служит для ограничения времени, отпускаемого на поиск решения задачи. В поле можно ввести время (в секундах) не превышающее 32767; значение 100, используемое по умолчанию, подходит для решения большинства лабораторных работ.
Поле Предельное число итераций
служит для управления временем решения задачи, путём ограничения числа промежуточных вычислений. В поле можно ввести время (в секундах) не превышающее 32767; значение 100, используемое по умолчанию, подходит для решения большинства простых задач.
При достижении отведённого временного интервала или при выполнении отведённого числа итераций, на экране появляется диалоговое окно Текущее состояние поиска решения.
Поле Относительная погрешность
служит для задания точности (допустимой погрешности), с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 (нуля) до1. Низкая точность соответствует введённому числу, содержащему меньшее количество десятичных знаков, чем число, используемое по умолчанию, например, 0,0001. Высокая точность увеличит время, которое требуется для того, чтобы сошёлся процесс оптимизации. Чем меньше введённое число, тем выше точность результатов.
Поле Допустимое отклонение
служит для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. При указании большого допуска поиск решения заканчивается быстрее.
Поле Сходимость
результатов поиска решения применяется только к нелинейным задачам. Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость
, поиск прекращается. Условием сходимости служит дробь из интервала от 0 (нуля) до 1. Лучшую сходимость характеризует большее количество десятичных знаков, например, 0,0001 – это меньшее относительное изменение, чем 0,01. Чем меньше его значение, тем выше точность результатов. Лучшая сходимость требует больше времени на поиск оптимального решения.
Флажок Линейная модель
служит для ускорения поиска решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи.
Флажок Неотрицательные значения
позволяет установить нулевую нижнею границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение
диалогового окна Добавить ограничение
.
Флажок Автоматическое масштабирование
служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.
Флажок Показывать результаты итераций
служит для приостановки поиска решения для просмотра результатов отдельных итераций.
Кнопки Оценки
служат для указания метода экстраполяции (линейная или квадратичная), используемого для получения исходных оценок значений переменных в каждом одномерном поиске.
Линейная
служит для использования линейной экстраполяции вдоль касательного вектора.
Квадратичная
служит для использования квадратичной экстраполяции, которая даёт лучшие результаты при решении нелинейных задач.
Кнопки Разности
(производные) служат для указания метода численного дифференцирования (прямые или центральные производные), который используется для вычисления частных производных целевых и ограничивающихся функций.
Прямые
используется для гладких непрерывных функций.
Центральные
используется для функций, имеющих разрывную производную. Не смотря на то, что данный способ требует больше вычислений, он может помочь при получении итогового сообщения о том, что процедура поиска решения не может улучшить текущий набор влияющих ячеек.
Кнопки Метод поиска
служат для выбора алгоритма оптимизации (метод Ньютона или сопряжённых градиентов).
Кнопка Ньютона
служит для реализации квазиньютоновского метода, в котором запрашивается больше памяти, но выполняется меньше итераций, чем в методе сопряжённых градиентов. Здесь вычисляются частные производные второго порядка.
Кнопка Сопряжённых градиентов
служит для реализации метода сопряжённых градиентов, в котором запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.
Для решения линейных задач используются алгоритмы симплексного метода. Для решения целочисленных задач используется метод ветвей и границ.
Команда Сохранить модель
служит для отображения на экране диалогового окна Сохранить модель,
в котором можно задать ссылку на область ячеек, предназначенную для хранения модели оптимизации. Данный вариант предусмотрен для хранения на листе более одной модели оптимизации. Первая модель сохраняется автоматически.
Команда Загрузить модель
служит для отображения на экране диалогового окна Загрузить модель,
в котором можно задать ссылку на область ячеек, содержащих загружаемую модель.
Сохранение и загрузка модели
1. Сохранение модели оптимизации
- В меню Сервис
выберите команду Поиск решения.
- Нажмите кнопку Параметры.
- Нажмите кнопку Сохранить модель.
Появляется окно Сохранить модель,
рис. 4.
- В поле Задайте область модели
введите ссылку на верхнюю ячейку столбца, в котором хотите разместить модель оптимизации.

Рис. 4. Диалоговое окно
Сохранить модель.
Значения элементов управления диалоговых окон Поиск решения
и Параметры поиска решения
записываются на лист. Чтобы использовать на листе несколько моделей оптимизации, нужно сохранить их в разных диапазонах (столбцах).
Предлагаемый диапазон содержит ячейку для каждого ограничения, а также ещё три ячейки. Можно также ввести ссылку только на верхнюю ячейку столбца, в котором следует сохранить модель.
Диалоговое окно Загрузить модель
используется для задания ссылки на область загружаемой модели оптимизации. Ссылка должна адресовать область модели целиком, недостаточно указать только первую ячейку.
2. Загрузка модели оптимизации
Перед тем как использовать данную процедуру, необходимо сохранить хотя бы одну модель.
1 В меню Сервис
выберите команду Поиск решения.
2. Нажмите кнопку Параметры.
3. Нажмите кнопку Загрузить модель.
Появляется окно, аналогичное окну Сохранить модель.
4. Введите ссылку на область модели.
Диалоговое окно Загрузить модель
используется для задания ссылки на область загружаемой (ранее сохранённой) модели оптимизации. Ссылка должна адресовать область модели целиком не достаточно указать только первую ячейку.
Вычисления и результаты решения задачи
Для запуска оптимизатора нажмите кнопку Выполнить в окне Поиск решения.
Программа начинает работать, в строке сообщений (слева внизу листа) появляется сообщение Постановка задачи… Ваша таблица с моделью и параметрами алгоритма автоматически приводится к стандартам постановки задач математического программирования. Это преимущество Excel. В других пакетах Вам пришлось бы оторваться от экономической сути задачи и заниматься формальной математической постановкой задачи. После этапа постановки решается задача.
Чтобы прервать поиск решения, нажмите клавишу ESC. Microsoft Excel пересчитает лист с учётом найденных значений влияющих ячеек.
По окончании счёта появляется диалоговое окно Результаты поиска решения, рис. 5.

Рис. 5. Диалоговое окно
Результаты поиска решения.
Нажав соответствующую кнопку можно сохранить найденное решение во влияющих ячейках модели или восстановить исходные значения.
Поле Тип отчёта
служит для указания типа отчёта, размещаемого на отдельном листе книги.
Отчёт Результаты
используется для создания отчёта, состоящего из целевой ячейки и списка влияющих ячеек модели, их исходных и конечных значений, а также формул ограничений и дополнительных сведений о наложенных ограничениях.
Отчёт Устойчивость
используется для создания отчёта, содержащего сведения о чувствительности решения к малым изменениям в формуле модели или в формулах ограничений. Такой отчёт не создаётся для моделей, значения в которых ограничены множеством целых чисел. В случае нелинейных моделей отчёт содержит данные для градиентов и множителей Лагранжа. В отчёт по нелинейным моделям включаются ограниченные затраты, фиктивные цены, а также диапазоны ограничений.
Отчёт Пределы
используется для создания отчёта, состоящего из целевой ячейки и списка влияющих ячеек модели, их значений, а также нижних и верхних границ. Такой отчёт не создаётся для моделей, значения в которых ограничены множеством целых чисел. Нижним пределом является наименьшее значение, которое может содержать влияющая ячейка, в то время как значения остальных влияющих ячеек фиксированы и удовлетворяют наложенным ограничениям. Соответственно верхним пределом называется наибольшее значение.
К сожалению, эти отчёты очень неудобны. Они перегружены плохо читаемыми абсолютными ссылками со знаками доллара. Желает лучшего и перевод с английского на русский.
Кнопка Сохранить сценарий
служит для отображения диалогового окна Сохранение сценария
, в котором можно сохранить сценарий решения задачи, чтобы использовать его в дальнейшем с помощью диспетчера сценариев Microsoft Excel. В поле Название сценария
введите имя сценария. Чтобы создать сценарий, не сохраняя найденное решение и не отображая результатов на листе, сохраните сценарий в диалоговом окне Результаты поиска решения
, а затем выберите Восстановить исходные
значения.
Просмотр промежуточных результатов поиска решения
Режим пошагового решения задач используется при отладке моделей.
В диалоговом окне Поиск решения
нажмите кнопку Параметры.
Чтобы получить возможность просмотра текущих значений влияющих ячеек каждой итерации, установите флажок Показывать результаты итераций,
нажмите кнопку ОК, а затем кнопку Выполнить.
На экране появится диалоговое окно Текущее состояние поиска решения
, рис. 6, а влияющие ячейки листа изменят свои значения.
Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения,
нажмите кнопку Стоп.

Рис.6. Диалоговое окно
Текущее состояние поиска решения.
Чтобы выполнить следующую итерацию и просмотреть её результаты, нажмите
кнопку Продолжить.
Возникающие проблемы и сообщения процедуры поиска решения
Оптимальное решение не найдено
Поиск решения может остановиться до достижения оптимального решения по следующим причинам.
Пользователь прервал процесс поиска.
Команда Показывать результаты итераций
в диалоговом окне Параметры
поиска решения выбрана перед Выполнить.
Пользователь нажал кнопку Стоп
в режиме пошагового выполнения итераций, по истечении времени, отведённого на работу процедуры, или после выполнения заданного числа итераций.
Установлен флажок Линейная модель
в диалоговом окне Параметры
поиска решения, в то время как решаемая задача не линейна.
Значение, заданное в поле Установить целевую
диалогового окна Поиск решения
, неограниченно увеличивается или уменьшается. Необходимо уменьшить значения полей Максимальное время
или Итерации
в диалоговом окне Параметры поиска решения.
В случае задач, значения в которых ограничены множеством целых чисел, необходимо уменьшить значение в поле Допустимое отклонение
диалогового окна Параметры поиска решения
, что позволит найти лучшее решение.
В случае нелинейных задач необходимо уменьшить значение в поле Сходимость
диалогового окна Параметры поиска решения
, что позволит продолжать поиск решения, когда значение в целевой ячейке изменяется медленно.
Если значения влияющих ячеек или значения влияющей и целевой ячеек различаются на несколько порядков, необходимо установить флажок Автоматическое масштабирование
в диалоговом окне Параметры поиска решения.
Внесите нужные изменения и запустите процедуру поиска решения снова.
Если найденное решение нелинейной задачи существенно отличается от ожидаемого результата, запустите процедуру поиска решения с другими начальными значениями влияющих ячеек. Если задать такие значения влияющих ячеек, которые близко расположены от экстремальной точки целевой функции, можно значительно сократить время поиска решения.
Итоговые сообщения процедуры поиска решения
1. Если поиск решения успешно завершён, в диалоговом окне Результаты поиска решения
выводится одно из следующих сообщений.
Решение найдено. Все ограничения и условия оптимальности выполнены.
Все ограничения соблюдены с установленной точностью и найдено заданное значение целевой ячейки.
Поиск свёлся к текущему решению. Все ограничения выполнены.
Относительное изменение значения в целевой ячейке за последние пять итераций стало меньше установленного значения параметра Сходимость
в диалоговом окне Параметры поиска решения
. Чтобы найти более точное решение, установите меньшее значение параметра Сходимость
, но это займёт больше времени.
2. Если поиск не может найти оптимальное решение, в диалоговом окне Результаты поиска решения
выводится одно из следующих сообщений.
Поиск не может улучшить текущее решение. Все ограничения выполнены.
В процессе поиска решения нельзя найти такой набор значений влияющих ячеек, который был бы лучше текущего решения. Приблизительное решение найдено, но либо дальнейшее уточнение невозможно, либо заданная погрешность слишком высока. Измените погрешность на меньшее число и запустите процедуру поиска решения снова.
3. Поиск остановлен (истекло заданное на поиск время).
Время, отпущенное на решение задачи, исчерпано, но достичь удовлетворительного решения не удалось. Чтобы при следующем запуске процедуры поиска решения не повторять выполненные вычисления, установите переключатель Сохранить найденное
решение
или Сохранить сценарий
.
4. Поиск остановлен (достигнуто максимальное число итераций).
Произведено разрешённое число итераций, но достичь удовлетворительного решения не удалось. Увеличение числа итераций может помочь, однако следует рассмотреть результаты, чтобы понять причины остановки. Чтобы при следующем запуске процедуры поиска решения не повторять выполненные вычисления установите переключатель Сохранить найденное
решение
или Сохранить сценарий
.
5. Значения целевой ячейки не сходятся.
Значение целевой ячейки неограниченно увеличивается (или уменьшается), даже если все ограничения соблюдены.Возможно, следует в задаче снять одно ограничение или сразу несколько, или наложить дополнительные ограничения. Изучите процесс расхождения решения, проверьте ограничения и запустите задачу снова. Например, в задаче об оптимальных портфелях банков, если не наложить ограничение на портфель привлечения ресурсов, то банк как аферист будет занимать деньги до бесконечности.
6. Поиск не может найти подходящее решение.
В процессе поиска решения нельзя сделать итерацию, которая удовлетворяла бы всем ограничениям при заданной точности. Вероятно, ограничения противоречивы. Исследуйте лист на предмет возможных ошибок в формулах ограничений или в выборе ограничений.
7. Поиск остановлен по требованию пользователя.
Нажата кнопка Стоп в диалоговом окне Текущее состояние поиска решения
после прерывания поиска решения в процессе выполнения итераций.
8. Условия для линейной модели не удовлетворяются.
Установлен флажок Линейная модель
, однако итоговый пересчёт порождает такие значения, которые не согласуются с линейной моделью. Это означает, что решение недействительно для данных формул листа. Чтобы проверить линейность задачи, установите флажок Автоматическое масштабирование и повторно запустите задачу. Если это сообщение опять появится на экране, снимите флажок Линейная модель
и снова запустите задачу.
9. При поиске решения обнаружено ошибочное значение в целевой ячейке или в ячейке ограничения.
При пересчёте значений ячеек обнаружена ошибка в одной формуле или в нескольких сразу. Найдите целевую ячейку или ячейку ограничения, порождающие ошибку, и измените их формулы так, чтобы они возвращали подходящее числовое значение.
Набрано неверное имя или формула в окне Добавить ограничение или окне Изменить ограничение или в поле Ограничения были заданы целое или двоичное ограничение. Чтобы ограничить значения ячейки множеством целых чисел, выберите оператор целого ограничения в списке условных операторов. Чтобы установить двоичное ограничение, выберите оператор для двоичного ограничения.
10. Мало памяти для решения задачи.
Система не смогла выделить память, необходимую для поиска решения. Закройте некоторые файлы или приложения, и попытайтесь снова выполнить процедуру поиска решения.
Примеры выполнения задач
ПРИМЕР № 1
Для изготовления четырёх видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.
Какое количество продукции каждого вида должно изготовляться, чтобы доход от реализации был максимальным?
| Тип сырья
|
Нормы расхода сырья на одно изделие
|
Запасы сырья
|
| А
|
Б
|
В
|
Г
|
| I
|
1
|
2
|
1
|
0
|
18
|
| II
|
1
|
1
|
2
|
1
|
30
|
| III
|
1
|
3
|
3
|
2
|
40
|
| ЦЕНА ИЗДЕЛИЯ
|
12
|
7
|
18
|
10
|
Решение
1. Формулировка математической модели задачи
:
· переменные для решения задачи: x
1
– суточный объём изготовления продукции А, x
2
– суточный объём изготовления продукции Б, x
3
– суточный объём изготовления продукции В, x
4
–
суточный объём изготовления продукции Г;
· определение функции цели (критерия оптимизации). Суммарная суточная прибыль от изготовления всех видов продукции равна:
F=12* x1
+7* x2
+18* x3
+10* x4,
поэтому цель состоит в том, чтобы среди всех допустимых значений x1,
x2,
x3,
x4
найти такие, которые максимизируют суммарную прибыль от изготовления продуктов F:
 F=12* x1
+7* x2
+18* x3
+10* x4
max; F=12* x1
+7* x2
+18* x3
+10* x4
max;
· ограничения на переменные:
1. объём производства продукции не может быть отрицательным, т. е.
x1
≥ 0, x2
≥ 0, x3
≥ 0, x4
≥ 0;
2. расход исходного продукта для изготовления всех видов продукции не может превосходить максимально возможного запаса данного исходного продукта, т. е.
1* x1
+2* x2
+1* x3
+0* x4
≤ 18,
1* x1
+1* x2
+2* x3
+1* x4
≤ 30,
1* x1
+3* x2
+3* x3
+2* x4
≤ 40,
Таким образом, получаем следующую математическую модель задачи:
· Найти максимум следующей функции:
 F=12* x1
+7* x2
+18* x3
+10* x4
max; F=12* x1
+7* x2
+18* x3
+10* x4
max;
· При ограничениях вида:
1* x1
+2* x2
+1* x3
+0* x4
≤ 18,
1* x1
+1* x2
+2* x3
+1* x4
≤ 30,
1* x1
+3* x2
+3* x3
+2* x4
≤ 40,
x1
≥ 0, x2
≥ 0, x3
≥ 0, x4
≥ 0;
2. Подготовка листа рабочей книги
MS
Excel для вычислений
–
на рабочий лист вводим необходимый текст, данные и формулы в соответствии с рис. 7. Переменные задачи x1,
x2,
x3,
x4
находятся соответственно в C3, С4, С5, С6 . Целевая функция находится в ячейке С8 и содержит формулу:
=12*C3+7*C4+18*C5+10*C6
Ограничения на задачу учтены в ячейках С10:С12.
3. Работа с надстройкой Поиск решения
– воспользовавшись командой Сервис |
Поиск решения,
вводим необходимые данные для рассматриваемой задачи (установка данных в окне Поиск решения приведена на рис. 8). Результат работы по поиску решения помещён на рис. 9 – 14.

Рис. 7. Рабочий лист
MS
Excel
для решения задачи
.

Рис. 8. Установка необходимых параметров задачи
в окне Поиск решения
.
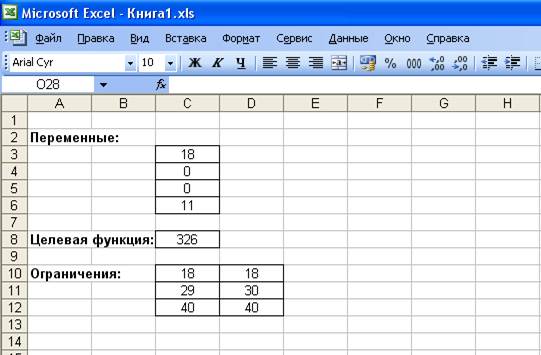
Рис.9. Результаты расчёта надстройки
Поиск решения.

Рис. 10. Отчёт по результатам
поиска решения.
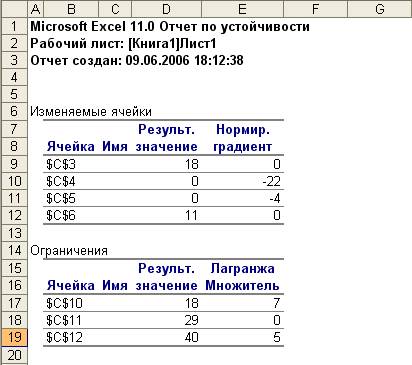
Рис. 11. Отчёт по устойчивости
поиска решения.

Рис. 12. Отчёт по пределам
поиска решения.
ВЫВОД
:
из решения видно, что оптимальный план выпуска предусматривает изготовление продукции видов "А" и "Г". А продукцию видов "Б" и "В" производить не стоит. Полученная Вами прибыль составит 326 усл. ед.
ПРИМЕР №
2
Задача распределения ресурсов
Предприятие изготавливает и продает краску двух видов: для внутренних и внешних работ. Для производства краски используется два исходных продукта A и B. Расходы продуктов A и B на 1 т. соответствующих красок и запасы этих продуктов на складе приведены в таблице:
| Исходный
|
Расход продуктов (в тоннах на 1 т. краски)
|
Запас продукта на
|
| продукт
|
краска для внутренних работ
|
краска для внешних работ
|
складе
( тонн )
|
| A
|
1
|
2
|
3
|
| B
|
3
|
1
|
3
|
Продажная цена за 1 тонну краски для внутренних работ составляет 2 000 рублей, краска для наружных работ продается по 1 000 рублей за 1 тонну. Требуется определить какое количество краски каждого вида следует производить предприятию, чтобы получить максимальный доход.
Рассмотрим поэтапное решение этой задачи графическим способом с использованием процедуры « Поиск решения » Excel.
I.
Составление математической модели задачи.
1) Переменные задачи.
Обозначим: x1
- количество производимой краски для
внутренних работ;
x2
- соответствующее количество краски
для наружных работ.
2) Ограничения,
которым должны удовлетворять переменные задачи:
x1
, x2
 0;
0;
по расходу продукта A: x1
+ 2x2
 3; 3;
по расходу продукта B: 3x1
+ x2
 3; 3;
В левых частях последних двух неравенств определены расходы продуктов A и B, а в правых частях неравенств записаны запасы этих продуктов.
3) Целевая функция задачи.
Обозначим Z доход от продажи краски (в тысячах рублей), тогда целевая функция задачи записывается так:
Z = 2x1
+ x2
,
таким образом, задача состоит в том, чтобы найти max Z=2x1
+x2
, при ограничениях:
x1
+ 2x2
 3 (A) 3 (A)
3x1
+ x2
 3 (B) 3 (B)
x1
, x2
 0 .
0 .
Так как переменные задачи x1
и x2
входят в целевую функцию и ограничения задачи линейно
, то соответствующая задача оптимизации называется задачей линейного программирования (ЛП)
В рассматриваемом примере содержатся только две переменные x1
и x2
, поэтому задачу можно решить графически.
1) На плоскости x1
, x2
строим область допустимых значений переменных, определяемую ограничениями задачи:
x1
+ 2x2
 3 (A) 3 (A)
3x1
+ 1x2
 3 (B) 3 (B)
x1
, x2
 0 .
0 .
Последнее ограничение определяет первый квадрант плоскости. Чтобы построить множество точек удовлетворяющих неравенству (А) нанесем на плоскость график прямой, определяющий границу этого множества: x1
+2x2
=3 (A).
Приведем это уравнение к виду:  . А это уравнение прямой «в отрезках» и для построения этой прямой используются две точки (a , 0) и (0 , b). (См. рисунок 11). . А это уравнение прямой «в отрезках» и для построения этой прямой используются две точки (a , 0) и (0 , b). (См. рисунок 11).
b
a 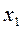
Рис.11.
Проведя уравнение (A) к виду прямой в отрезках, получим:

Аналогично, для ограничения (B) уравнение прямой в отрезках будет:
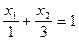
Построим обе прямые на плоскости. Множества точек, удовлетворяющие неравенствам (A) и (B) будут полуплоскости, лежащие под соответствующими прямыми, а множество допустимых значений переменных будет пересечением (общей частью) этих полуплоскостей, лежащее в первом квадранте: четырехугольник ABCD (см. рис.12)
  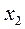
 3 3
2 (B)
 B B
 C C
      1 (A) 1 (A)
  1 2 1 2
Рис.12.
2) На множестве допустимых решений (ABCD) найдем точку, в которой целевая функция Z=2x1
+x2
имеет максимальное значение. Для этого посмотрим линии уровня
целевой функции. Линией уровня называется множество точек, на которых функция принимает постоянное значение:
Z = 2x1
+ x2
= К ,
где К - задаваемая постоянная.
При К = 1 уравнение линии уровня будет:
2x1
+ x2
= 1
или (в отрезках) :
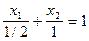
При К = 2, аналогично:
2x1
+ x2
= 2 , или  . .
Нанеся линии уровня на область допустимых решений (рис.13), получим, что при увеличении значения Z соответствующая линия уровня перемещается параллельно предыдущей вправо и вверх. Таким образом, точкой из многоугольника ABCD в которой целевая функция Z имеет максимальное значение будет вершина С. Эта точка и определяет решение задачи.
3

(B) B
 C C
   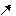      1 (A) 1 (A)

 1 2 3
Рис. 13.
3) Вычисление координат оптимальной точки (С).
Точка C лежит на пересечении прямых (A) и (B), поэтому, чтобы определить ее координаты надо решить систему уравнений:
 x1
+ 2x2
= 3 (A) x1
+ 2x2
= 3 (A)
3x1
+ x2
= 3 (B)
Решение:
x1
*
= 0.6 ; x2
*
= 1.2 ;
максимальное значение Z:
Z*
= 2*0.6 + 1.2 = 2.4.
Вывод
Надстройка Поиск решения
в Microsoft Excel даёт возможность найти решение, оптимальное при нескольких входных значениях и наборе ограничений на решение. Программа Поиск решения
содержит параметры, управляющие процессом поиска решения: максимальное время, число итераций, точность, допустимое отклонение. Каждый из этих параметров имеет значение по умолчанию, подходящее для большинства задач. Использование новых установок параметров обычно необходимо для проведения серьёзных исследований сложных систем управления. Диспетчер сценариев способен запомнить несколько решений, найденных данным средством, и сгенерировать на этой основе отчёт. Надстройка Поиск решения
готовит три вида отчётов, которые характеризуют найденное решение задачи: отчёт по результатам, отчёт по устойчивости и отчёт по пределам. Режим пошагового поиска позволяет наблюдать последовательность приближений к оптимальному решению задачи. Во многих случаях это помогает «почувствовать» сходимость процесса и установить причины неудач и тупиков при поиске оптимального решения. В результате поиска решения EXCEL выводит сообщения о том, удалось ли получить оптимальное решение задачи.
С помощью надстройки Поиск решения
можно решать как линейные задачи (задачи линейного, целочисленного и стохастического программирования), так и нелинейные (задачи нелинейного программирования), а также системы нелинейных уравнений. Для успешной работы средства Поиск решения
следует стремиться к тому, чтобы зависимости были гладкими или, по крайней мере, непрерывными.
Поиск решения
можно использовать и для решения задач математического программирования других типов, но в этом случае процедура поиска часто заканчивается неудачей, а при благоприятном исходе находит лишь один из локальных оптимумов. Поэтому решение таких задач с помощью данной процедуры следует предварять их аналитическим исследованием на предмет свойств области допустимых решений, чтобы выбрать подходящие начальные значения и сделать правильное заключение о качестве и практической применимости полученного решения.
Список литературы
1. Л. В. Рудикова «Microsoft Excel для студента», Санкт – Петербург, БХВ-Петербург, 2005;
2. «Лабораторные работы на персональном компьютере» И. Ф. Цисарь, издательство «Экзамен», Москва, 2002;
3. Додж М. и др. «Эффективная работа с Microsoft Excel», 2000.СПб.:Питер, 2001.
4. Солодовников А. С. «Введение в линейную алгебру и линейное программирование». Москва, издательство «Просвещение», 1966. – 184 с.
5. Стрейвер А. «Теория линейного и целочисленного программирования» в двух томах, том 1: перевод с английского. – Москва: Мир, 1991. – 360 с.
6. Ашманов С.А.«Линейное программирование». - М.: Наука, 1981.
7. Банди Б. «Основы линейного программирования»: Пер. с англ. - М.: Радио и связь, 1989.
8. Кораблин М. А. «Информатика поиска управленческих решений», Москва, СОЛОН-Пресс, 2003.
9. Габасов Р., Кириллова Ф.М. Методы линейного программирования. Ч.1. Общие задачи, Минск, Изд-во БГУ им. В.И. Ленина, 1977. - 176 с.
|