Исследования движения тел в диссипативной среде
Приборы и принадлежности:
сосуд с исследуемой жидкостью, шарики большой плотности, чем плотность жидкости, секундомер, масштабная линейка.
Цель работы:
изучение движения тела в однородном силовом поле при наличии сопротивления среды и определение коэффициента трения (вязкости) среды.Исследуемые закономерности.
На достаточно маленький твердый шарик, падающий в вязкой жидкости, действуют три силы:
1). Сила тяжести
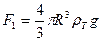 (1) (1)
Где R - радиус шарика; 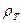 - плотность шарика; - плотность шарика;
2). Выталкивающая сила ( сила Архимеда )
 (2) (2)
где 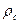 - плотность жидкости; - плотность жидкости;
3). Сила сопротивления среды ( сила Строкса )
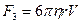 (3) (3)
Где 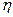 - вязкость жидкости; - вязкость жидкости; 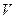 - скорость падения шарика. - скорость падения шарика.
Формула (3) применима к твердому шарику, окруженному однородной жидкостью, при условии, что скорость шарика невелика и расстояние до границ жидкости значительно больше, чем диаметр шарика.
Результирующая сила
 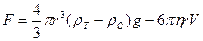 (4) (4)
В нашем случае, при 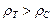 , пока скорость , пока скорость 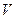 невелика, шарик будет падать с ускорением. По достижении определенной скорости невелика, шарик будет падать с ускорением. По достижении определенной скорости 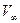 , при которой результирующая сила обращается в нуль, движение шарика становится равномерным. Скорость равномерного движения можно определить из условия: , при которой результирующая сила обращается в нуль, движение шарика становится равномерным. Скорость равномерного движения можно определить из условия:
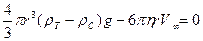 (5) (5)
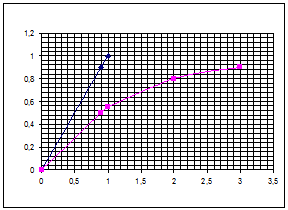
Время, за которое тело могло бы достичь стационарной скорости 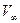 , двигаясь с начальным ускорением , двигаясь с начальным ускорением 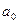 *, называют временем переходного процесса (или временем релаксации *, называют временем переходного процесса (или временем релаксации 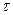 ) (смотри рисунок). ) (смотри рисунок).
Временная зависимость 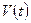 на всех этапах движения описывается выражением на всех этапах движения описывается выражением
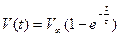 (6) (6)
Определив установившуюся скорость 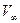 равномерного падения шарика, можно из соотношения (5) найти коэффициент вязкости жидкости равномерного падения шарика, можно из соотношения (5) найти коэффициент вязкости жидкости
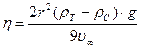 (7) (7)
или
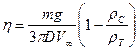 (8) (8)
Где D - диаметр шарика; 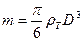 - его масса. - его масса.
Коэффициент 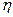 численно равен силе трения между соседними слоями при единичной площади соприкосновения слоёв и единичном градиенте скорости в направлении, перпендикулярном слоям. Единицей вязкости служит численно равен силе трения между соседними слоями при единичной площади соприкосновения слоёв и единичном градиенте скорости в направлении, перпендикулярном слоям. Единицей вязкости служит 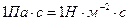 . .
В установившемся режиме движения сила трения и сила тяжести ( с учётом силы Архимеда ) равны друг другу и работа силы тяжести переходит целиком в теплоту. Диссипация энергии за 1 с ( мощность потерь ) находят как 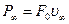 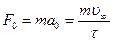 , таким образом , таким образом
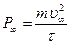 (9) (9)
Методика эксперимента
Телом, движение которого наблюдают, служит шарик (D<5мм), а средой - вязкие жидкости. Жидкость наполняет цилиндрический сосуд с двумя поперечными метками на разных уровнях. Измеряя время падения шарика на пути 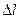 от одной метки до другой, находят его среднюю скорость. Найденное значение можно отождествить с установившейся от одной метки до другой, находят его среднюю скорость. Найденное значение можно отождествить с установившейся 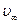 , если расстояние от верхней метки до уровня жидкости превышает путь релаксации , если расстояние от верхней метки до уровня жидкости превышает путь релаксации 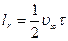 (смотри рисунок). Масса шарика определяется взвешиванием на аналитических весах. (смотри рисунок). Масса шарика определяется взвешиванием на аналитических весах.
Реклама

Обработка результатов
| № |
1 |
2 |
3 |
4 |
5 |
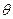 |
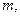 кг кг |
113*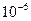 |
114*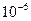 |
112*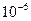 |
120*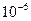 |
117*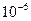 |
0,5*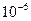 |
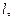 м м |
0,2 |
0,2 |
0,2 |
0,2 |
0,2 |
0,5*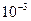 |
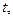 с с |
5,86 |
5,87 |
5,55 |
5,37 |
5,45 |
0,5*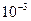 |
Вычислим скорость прохождения шарика между слоями в сосуде
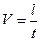 , , 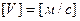 : :
1.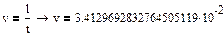
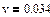
2.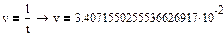
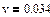
3.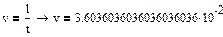
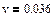
4.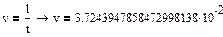
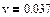
5.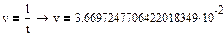
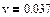
Определим вязкость среды (через диаметр), зная, что
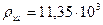 кг/м3
, а кг/м3
, а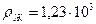 кг/м3 кг/м3
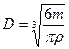 , , 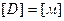
1. 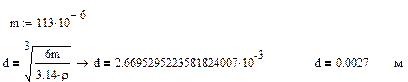
2. 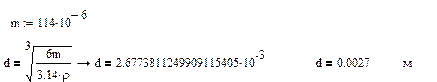
3. 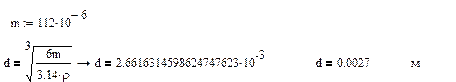
4. 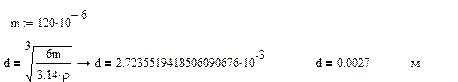
5. 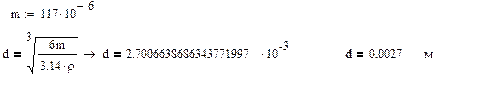
Вычисляем вязкость среды по формуле
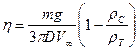 , , 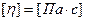 : :
1. 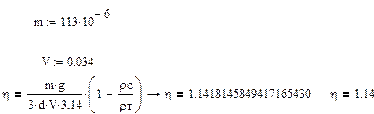
2. 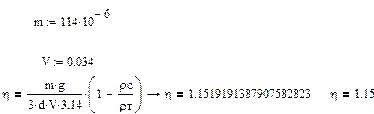
3. 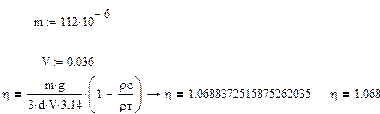
4. 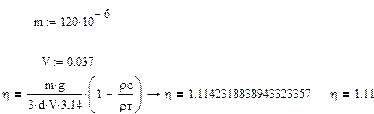
5. 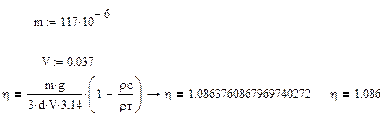
Определим время релаксации:
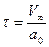 , где , где 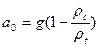 , , 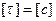 , , 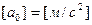
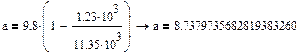
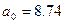 м/ м/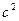
1. 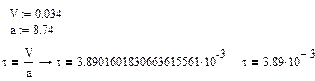
2. 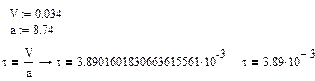
3. 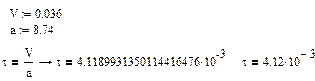
4. 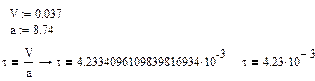
5. 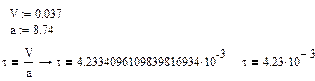
Расчет мощности потерь
:
[P]=[Вт]
1. 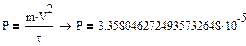
2. 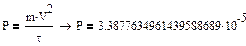
3. 
4. 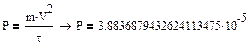
5. 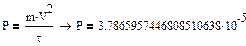
Полученные значения вязкости жидкости образуют выборку в порядке возрастания
| данные |
1,068 |
1,086 |
1,11 |
1,14 |
1,15 |
Проверим выборку на наличие грубых погрешностей.
Предположим, что промахи исключены.
R (размах выборки)=׀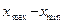 ׀=1.15-1.068=0,082 ׀=1.15-1.068=0,082
Для N=5 и Р=95% существует 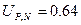
U=׀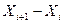 ׀/R ׀/R
U=׀1.14-1.11׀/0.082=0.036
U=׀1.15-1.14׀/0.082=0.012
Следовательно, промахов в выборке нет.
Рассчитаем среднее выборочное значение:
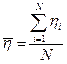
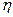 = 1,1108 = 1,1108
Вычислить выборочное среднее квадратическое отклонение
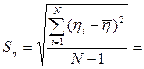 0,11 0,11
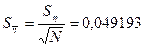
Вычисляем случайную погрешность:
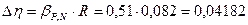
Приборная погрешность:
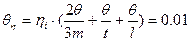
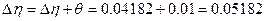
Окончательный результат:
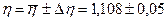
Вывод: при выполнении лабораторной работы мы изучили движение в диссипативной среде и рассчитали коэффициент внутреннего трения среды.
|