Задача 1
Для заданной механической системы определить ускорения грузов и натяжения в ветвях нитей, к которым прикреплены грузы. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Система движется из состояния покоя.

Данные:
1. G1
=2G, сила тяжести
2. G2
=G, сила тяжести
3. G3
=2G, сила тяжести
4. R/r=3
5. i2
x
=2r, радиус инерции
6. f =0.2, коэффициент трения скольжения
Решение

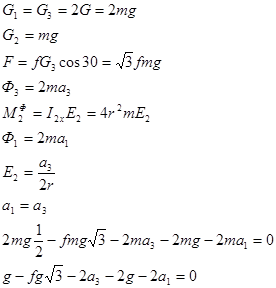
т.к. a1
=a3
тозаменим a1
=a3
=a

T3-2
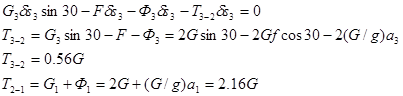
Задание
K
2
Движение груза 1 должно описываться уравнением 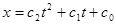 , где t-время (с), , где t-время (с), 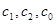 -некоторые постоянные. В начальный момент времени (t=0) положение груза определяется координатой -некоторые постоянные. В начальный момент времени (t=0) положение груза определяется координатой 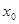 , и он имеет скорость , и он имеет скорость 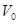 . Учесть, что в момент времени t=t2
координата груза равна . Учесть, что в момент времени t=t2
координата груза равна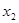 . Определить коэффициенты . Определить коэффициенты 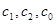 , при которых осуществляется требуемое движение груза 1. Определить также в момент времени t=t1,
скорость и ускорение груза и точки М одного из колес механизма. , при которых осуществляется требуемое движение груза 1. Определить также в момент времени t=t1,
скорость и ускорение груза и точки М одного из колес механизма.

Данные:
7. R2
=45,cм
8. r2
=35, см
9. R3
=105, см
10. x0
=8, см
11. V0
=5, см/с
12. x2
=124, см
13. t2
=4, см
14. t1
=3, см
Решение
Нахождение коэффициентов 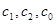
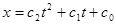 ; ; 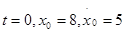 ; ; 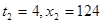 ; ;
Скорость груза 1:
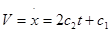
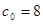 , , 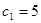 , , 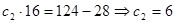
Уравнение движения груза 1:
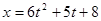
Скорость груза 1:
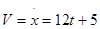 ; ;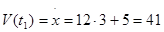
Ускорение груза 1:
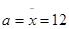
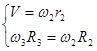 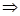 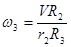 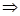 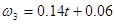
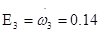 ; ; 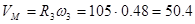
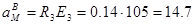
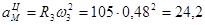
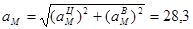
Результаты вычислений для заданного момента времени t=t1
| V, см/с |
а, см/с2
|
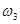 , рад/с , рад/с |
Е3
, рад/с2
|
VM
, см/с |
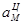 , см/с2 , см/с2
|
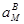 , см/с2 , см/с2
|
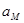 , см/с2 , см/с2
|
| 41 |
12 |
0,48 |
0,14 |
50,4 |
24,2 |
14,7 |
28,3 |

Вариант 6
Постановка задачи: Найти для заданного положения механизма скорости точек В и С, а также угловую скорость и угловое ускорение звена к которому эти точки принадлежат.

Дано: r = 15 cм, OA=40 см, AC=6 см, wOA
=1 рад/с, w1
=1 рад/с, eOA
=0 рад/с2
.
Найдем скорость точек С и В приняв за полюс точку А
Тогда скорости точек В и С запишутся как соответствующие суммы скоростей:
скорость полюса А во вращательном движении относительно точки о и скорость точки во вращательном движении относительно полюса А
Uc
=Ue
+Ur
где Ue=wOA
*OA; Ur=w2
*AC; Ur
=1*40=40 cм/c
Ub
=Ue
+Ur
где Ue=wOA
*OA; Ur=w2
*AB
Найдем угловую скорость w2
w2
=UA
/ACU
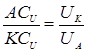 где UK
= w1
*OK ; ОК=ОА-rOK=40-15=25; UK
=1*25=25 cм/c; где UK
= w1
*OK ; ОК=ОА-rOK=40-15=25; UK
=1*25=25 cм/c;
КСU
=r-ACU
; UА
= wОА
*ОА =1*40=40; => 40ACU
=25*15-25ACU
=5.769 см
w2
=40/5.769=6.933
получаем скорости точек С и В:

UC
r
=6.933*6=41.59cм/c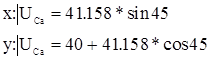
UCa
=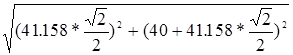 =194.978см/с =194.978см/с
UBr
=6.933*15=103.995 cм/c
UBa
=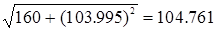 cм/c cм/c
Реклама

Найдем ускорения точек С и В
аа
=аA
+an
+at
аA
=wоа
2
*OA=40см/с2
; ткeOA
=0 то at
=0;
для точки С an
=w2
2
*AC=48.066*6=288.39 см/с2
;
аа
C
=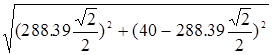 =331.71 =331.71
для точки Ban
=w2
2
*AВ=48.066*15=720.099 см/с2
;
аа
B
=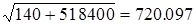 см/с2 см/с2
Вариант № 7

Точка М движется относительно тела D Определить абсолютную скорость и абсолютное ускорение точки М.
Дано: хе
=хе
(t)=3t+0.27t3
(см), t1
=10/3 (см), R=15 (см), jr
=0.15pt3
.
Решение
Примем за центр отсчета точку О- центр вала К тогда скорость центра в движении вдоль оси Х определится как Uе
= хе
`(t)=3+0.81t2
, а угловая скорость точки М во вращательном движении вокруг центра О определится как w=jr
`=0.45pt2
. Тогда относительная скорость точки М определится как Ur
=0.45pt2
*R.
Абсолютная скорость точки в момент времени t=10/3 =>
Ua
=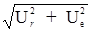 = =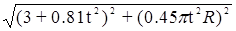 ==235.924 (см/c). ==235.924 (см/c).
Найдем абсолютное ускорение точки М.
aa
= ae
+ar
+acor
Переносное ускорение точки М:
аe
= Ue
`=1.62t.
Относительное ускорение
ar
=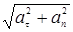 где аt
=Ur
`=0.9pt*R, an
=w2
*R. где аt
=Ur
`=0.9pt*R, an
=w2
*R.
ar
=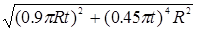
Кореалисово ускорение acor
=2wе
Ur
=0. т.к. wе
=const.
Т. к. ar
перпендикулярно ае
то
aa
=ar
+ ае
=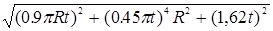
aa
(t=10/3)=381.37
Исходные данные приведены в таблице:
| m1
|
m2
|
m3
|
R3
,см |
α |
β |
f |
δ |
S,м |
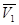 |
| m |
3m |
m |
28 |
30º |
45º |
0,10 |
0,2 |
1,5 |
? |
Применим к решению задачи теорему об изменении кинетической энергии механической системы:
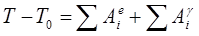 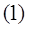 , где , где 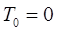 , т.к. в начале , т.к. в начале
система покоилась.
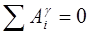 - сумма работ внутренних сил (нерастяжимых нитей абсолютно твердых тел). - сумма работ внутренних сил (нерастяжимых нитей абсолютно твердых тел).
Следовательно, уравнение (1) принимает вид
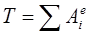 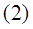
Вычислим кинетическую энергию системы:
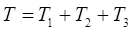 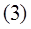
Тело 1 движется поступательно
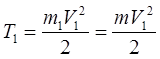
Тело 2 вращается вокруг оси Z
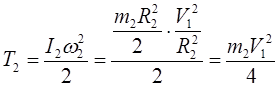 ; ; 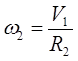
Тело 3 совершает плоскопараллельное движение, P-мгновенный центр скоростей
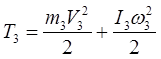 ; где ; где 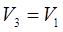 ; ;
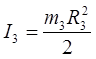 ; ; 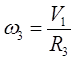
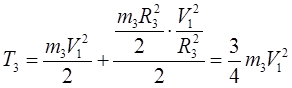
Подставим 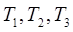 в в 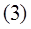 уравнение: уравнение:
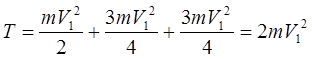
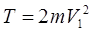 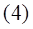
Найдем работу всех внешних сил при перемещении груза 1 на S1
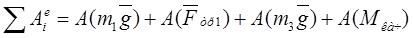
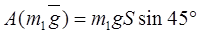
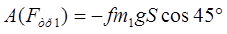
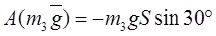
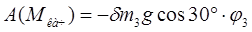 , ,
где 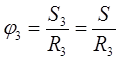 , , 
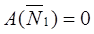 и и 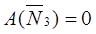 , т.к. , т.к. 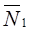 и и 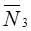 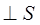
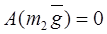 , т.к. центр масс неподвижен , т.к. центр масс неподвижен
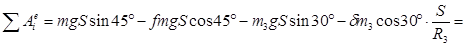 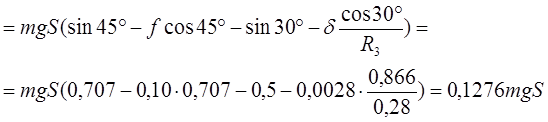
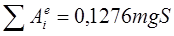 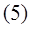
Подставим 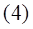 и и  во во  уравнение: уравнение:

ОТВЕТ: 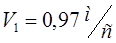
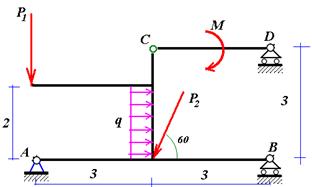
Рис. 1. Условие
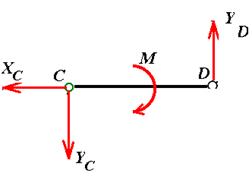
Рис. 2. Составим уравнения равновесия части CD
Xk
= Xc
= 0
Yk
= Yc
+ YD
= 0
Mc
= 3YD
M = 0
Составим уравнения равновесия части ACB
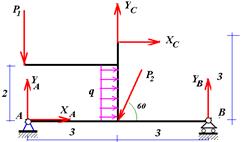
Рис. 3
Xk
= XA
+ Xc
P2
cos60 +2q=0
Yk
= YA
+ YB
+ Yc
P2
sin60 P1
= 0
MA
= 2q·1 + 6YB
3P2
sin60 +3Yc
3Xc
=0
Решаем систему уравнений и получаем (в кН) Xc
=0, Yc
=6.66, Xa
=0.5, Ya
=10.03, Yb
=0.364, Yd
=6.667.
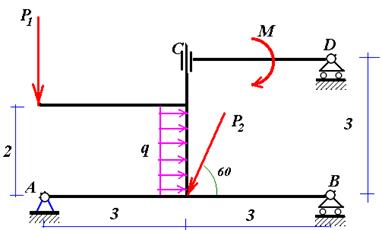
Рис. 4. Анализируя реакцию YB
, заменим шарнир на скользящую заделку. Из уравнения проекций на ось y для части CD получим Yd
=0.
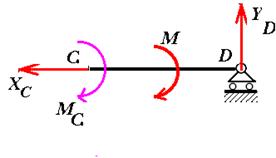
Рис. 5. Запишем сумму моментов для всей системы в целом относительно опоры A (Рис.
Реклама

6)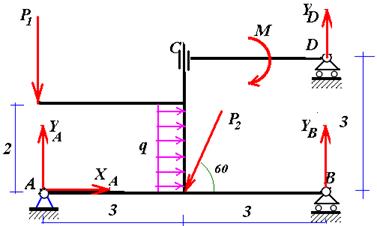
Рис. 6
MA
= 2q·1 + 6YB
3P2
sin60 M=0
Вычислим Yb
=7.031кН.
Вывод:
для первого способа соединения исследуемая реакция меньше.
|