Беляєвой Г.Д.
В умовах розбудови національної системи загальної середньої освіти важливе значення набуває інноваційна діяльність, яка характеризується системним експериментуванням, апробацією та застосуванням інновацій (нововведень) в освітньому процесі в ліцеї «Творчість».
Найбільш популярним є такі педагогічні технології: інформаційно-розвивальні, діяльні сні, розвивальні, особисто орієнтовані.
Метою особистісно орієнтованих технологій є формування активної, творчої особистості майбутнього фахівця, здатного самостійно будувати і коригувати свою аврально-пізнавальну діяльність. До цих технологій входять аудиторна і позааудіторна самостійна діяльність учнів, робота за індивідуальним планом, дослідницька робота метод проектів тощо.
В нашому ліцеї педагоги, як найбільш перспективну, впроваджують особистісно орієнтовану технологію навчання. Процес розробки і освоєння інновацій передбачає поетапну діяльність вчителя.
Ескпериментальну роботу над проблемою особистісно орієнтованого навчання учнів викладач математики розпочала у 2005 р. Вибір проблем був зумовлений переорієнтацією сучасної освіти як на особистість педагога, так і на особистість учнів. В умовах особистісно орієнтованого навчання відбувається становлення та розвиток таких важливих якостей особистостей, як рефлективність, критичність мислення, вміння працювати з інформацією, спілкуватися та нести відповідальність за наслідки спільної роботи.
Етапи роботи викладача математики Беляєвої Г.Д. над інноваційною проблемою можна описати наступним алгоритмом.
Алгоритм
роботи викладача математики над інноваційною проблемою
1. Вибір теми (проблеми) індивідуальної науково-методичної роботи:
- ознайомлення з літературою;
- ознайомлення з нормативними документами;
- вивчення прогресивного педагогічного досвіду з інноваційної проблеми.
2. Детальне ознайомлення з проблемою засобами літературних джерел:
- складання картотеки літературних джерел;
- виписки з літературних джерел;
3. Уточнення теми і розробка попереднього варіанта плану індивідуальної науково-методичної роботи:
- обґрунтування вибору теми;
- актуальність і новизна;
- відбір актуальних методів та засобів пошукової діяльності;
Реклама

- формування мети та завдань роботи;
- розробка календарного плану індивідуальної роботи.
4. Впровадження інновацій у практику власної педагогічної діяльності.
5. Аналіз та оцінка результатів індивідуального досвіду роботи над проблемою, формування висновків та пропозицій.
6. Літературне оформлення роботи, звіт про отримані результати перед колегами.
В інтенсифікації навчального процесу на уроках важливу роль відіграє комплексно-методичне забезпечення предмета.
Викладач обладнала й оснастила відповідно до вимог навчальної програми кабінет математики. У кабінеті є необхідні ТЗН, навчальна і методична література, якісна наочність. До кожного уроку розробила цікавий змістовий дидактичний мета ріал, за допомогою якого можна організувати ефективну самостійну роботу учнів, проконтролювати засвоєння ними програмного матеріалу.
Розробила також серію опорних конспектів, які містять короткий зміст навчального матеріалу до теми уроку, схеми, алгоритми, опорно-довідковий матеріал. Наведемо зразки опорного конспекту та алгоритму.
Зростання і спадання функціі
Опорний конспект
Означення. Функція У = f (x) називаеться зростаючою на деякому промежутку, якщо для будь-яких х1
і х2
, що належать, з умови х2
> х1
випливає, що f ( x2
) > f ( x1
).

Означення. Функция y = f ( x ) називається спадною на деякому проміжутку, якщо для будьяких х1
і х2
, ща належать проміжутку, з умови x2
> x1
випливає, що f( x2
) < f ( x1
)
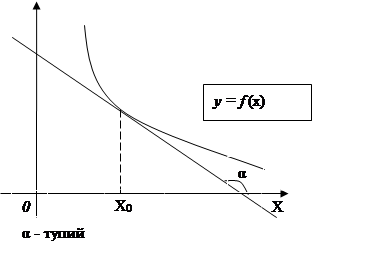
Геометричний змістпохідної tg α = f’ ( x0
)
tgα > 0
Властивість. Якщо функція y = f (x) дифе-
ренційована і зростає на деякому проміжутку, то її похідна на цьому проміжутку додатна або дорівнює нулю, тобто f ‘ (x) > 0 .
Ознака зростання функціі на проміжутку (достатня умова).
Якщо в кожній точці проміжутку f’(x) > 0 , то функція f(x) зростає на цьому проміжутку
|
tg α < 0
Властивість. Якщо функція y = f (x) диференційована і спадає на деякому проміжутку, то її похудна на цьому проміжутку від’ємна або дорівнює нулю, тобто f’(x0
) ≤ 0.
Ознака спадання функції на проміжутку (достатня умова).
Якщо в кожній точці проміжутку f’( x ) < 0 , то функція f(x) спадає на цьому проміжутку
|
| Проміжки зростання і спадання функції називають проміжками монотонності цієї функції. Якщо функція неперервна на кінцях промижутку, то його можна приєднати до проміжку монотонності функції |
ДОСЛІДЖЕННЯ ФУНКЦІЇ НА МОНОТОННІСТЬ
Алгоритм
| Алгоритм |
Приклад. f ( x ) = x3
– 3x2
|
| 1. Знайти область визначення заданної функції y = f (x) |
D( f ) = R, бо f (x) – многочлен |
| 2. Знайти похудну f’(x) |
f’ (x) = (x3
– 3x2
)’ = (x3
)’ – (3x2
)’ = 3x2
- 3·2x = 3x2
– 6x |
3. Розв’язати нерівності:
а) f’(x) > 0, указати проміжки зростання функції;
б) f’(x) < 0, указати проміжки спадання функції
|
а) f’ (x) > 0 ,
3x2
– 6x > 0 ,
3x( x-2 ) > 0.
Реклама

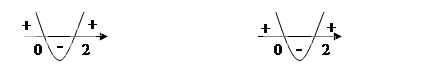
Зростає Спадає
(- ∞; 0 ) та (2; +∞) (0;2)
|
| 4. Записати відповідь |
Зростає на кожному з проміжків (- ∞; 0 ) та (2; +∞) ;
Спадає на (0;2)
|
У своїй роботі Л.К.Ожго особливу увагу приділяє удосконаленню методики проведення самостійних робіт (навчальних та контролюючих), які вона використовує на різних етапах проведення уроку (перевірка домашніх завдань, актуалізація опорних знань, вивчення та закріплення нового матеріалу та ін.)
Навчальна самостійна робота
Початковий рівень
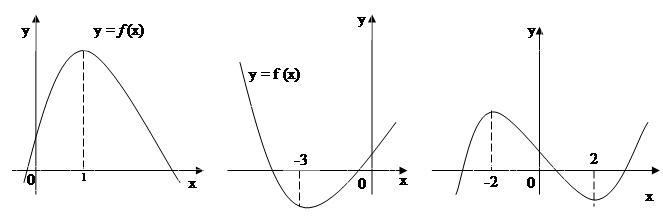
1) на малюнку зображено графік функції y = f (x) . Вкажіть проміжки : а) зростання; б) спадання.
Який знак має f ’ (x) на кожному з проміжків ?
1-й Варіант 2-й Варіант Зразок 
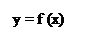 
Розв’язання
а) Фкнкція зростає на кожному з проміжків (- ∞; -2 ) та (2; +∞). На цих проміжках f’(x) > 0.
б) Функція спадає на проміжку (-2;2). На цьому проміжку f (x) < 0.
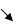 2. Проаналізуйте графік функції y = f (x) та заповнить таблицю. Користуйтесь такими позначками: 2. Проаналізуйте графік функції y = f (x) та заповнить таблицю. Користуйтесь такими позначками:
Функція зростає на проміжку - , спадає - , f’(x) > 0 – + , f’ (x) < 0 –
3. Відомо, що похідна функції y = f (x) має знаки, позначені на малюнку. Укажіть проміжки зростання та спадання функції.
1-й варіант2-й варіант Зразок
Дана функція зростає на кожному з проміжків (-∞;- 5) та (2;7) , спадає на кожному з проміжків (-5;1) , (-1;2) та (1; + ∞)
Середній рівень
1.Знайдіть проміжки монотонності функції.
1-й варіант 2-й варіант
y = - x2
+2x – 3 y = x2
– 2x +3
Зразок
Знайдіть проміжки монотонності функції y = - x2
+2x – 3
Розв’язання
1. D(y) = R
2. y’ = ( -x2
+ 4x + 1)’ = (-x2
)’ + (4x)’ + 1’ = -2x + 4 · 1 + 0 = -2x + 4
3. a) y’ >0, 6) y’ < 0,
-2x + 4 > 0, -2x + 4 < 0
-2x > -4, -2x < -4
x < 2 x>2
функція зростає функція спадає
Відповідь. Функція зростає на (-∞;2), спадає на (2; +∞).
2. Знайдіть проміжки зростання та спадання функції.
1-й варіант 2-й варіант
f (x) = x3
– 3x f (x) = x3
+ 3x
Зразок. Знайдіть проміжки зростання та спадання функції f (x) = x3
– 75x
Розв’язання
1.  D ( f ) = R D ( f ) = R
2. f’ (x) = (x3
– 75x)’ = (x3
)’ – (75x)’ = 3x2
– 75 · 1 = 3x2
– 75.
3. a) f’ (x) > 0,
3x2
– 75 > 0, + +
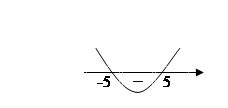
3( x + 5)(x - 5) > 0
 На (-∞;-5) та (5; +∞) функція зростає. На (-∞;-5) та (5; +∞) функція зростає.
б) f’ (x) < 0,
3x2
– 75 < 0, + +
3( x + 5)(x - 5) < 0
На (-5;5) функція спадає.
Відповідь. Функція зростає на ( -∞; - 5 ) та ( 5; + ∞ ), спадає на (-5; 5).
3. Знайдіть проміжки, на яких функція :
1-й варіант 2-й варіант
у = х3
+х2
– х – 1 у = х3
+ 2х2
+ х + 2 спадає.
Зразок. Знайдіть проміжки, на яких функція sy = 1/3 x3
– x2
– 3x + 5 зростає.
Розв’язання
1. D (y) = R
2. y’ = (1/3 x3
– x2
-3x + 5) = (1/3 x3
)’ – ( x2
)’ – ( 3x )’ + 5’ = x2
– 2x – 3 .
3. Треба знайти проміжки, на яких дана функція зростає, тобто y’ > 0.
x2
– 2x – 3 > 0,
x2
– 2x – 3 =0
D = (-2)2
– 4 · 1 · (-3) = 4 + 12 = 16.
x1
= -1 , x2
= 3
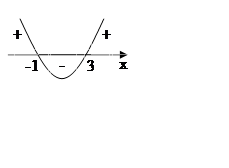 На (-∞; -1) та (3; + ∞) функція зростає На (-∞; -1) та (3; + ∞) функція зростає
Відповідь. Функція зростає на (-∞; -1) та (3; + ∞)
Достатній рівень
Знайдіть проміжки, на яких дана функція :
1-й варіант 2-й варіант
y = x2
+ 3x / x + 4 y = x2
– 3x / x – 4
Спадає Зростає
Зразок. Знайдить проміжки, на яких функція у = х2 – 6х / х + 2 спадає.
Розв’язання
1. D (y) : x + 2 ≠ 0 ; x ≠ -2.
2. y’ = (x2
-6x) ‘ (x + 2) – (x2
– 6x) (x + 2)’ / (x + 2)2
= (2x – 6) (x + 2) – (x2
– 6x) · 1 / (x + 2)2
=
= 2x2
+ 4x – 6x – 12 – x2
+ 6x / (x + 2)2
= x2
+ 4x – 12 / (x + 2)2
3. Треба зайти проміжки, на яких дана функція спадає, отже y’ < 0
x2
+ 4x – 12 = 0
D = 42
– 4· 1 · (-12) = 64,
x1
= -6 , x2
= 2
(x + 6)(x – 2) / (x + 2)2
< 0
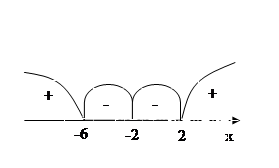 (x + 6)(x – 2) < 0 (x + 6)(x – 2) < 0
Знаки у‘ :
Дана функція спадає на кожному з проміжків (-6; - 2) та (-2;2).
Високий рівень
Знайдіть проміжки зростання та спадання функції :
1-й варіант 2-й варіант
у = (х – 3)3
/ х – 1 у = (х-1)3 / х + 3
Контролююча самостійна робота
Початковий рівень
1-й варіант
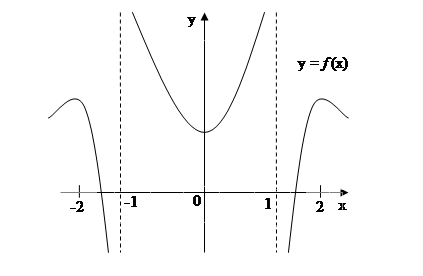
Користуючись графіком функції у = f (x), виберіть правильну відповідь.
Функція зростає на проміжку
А) (-2;-1). Б) (-1;0)
В) (0;1) В) (2; +∞)
2-й варіант
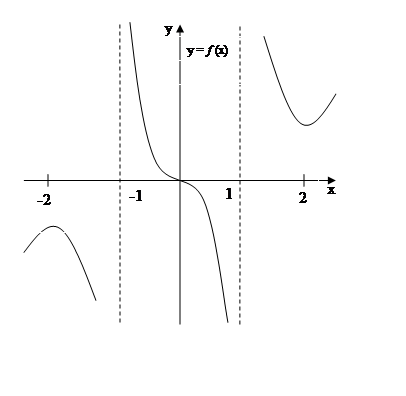
Користуючись графіком функції у = f (x), виберіть правильну відповідь.
Функція спадає на проміжку
А) (-∞; -2). Б) (-1;1).
В) (2; +∞). Г) (-∞;+∞)
Середній рівень
1-й варіант
Функція у = f (x) диференційована. За даними, наведеними в таблиці, визначте проміжки зростання та спадання функції.
| x |
(-∞; -7) |
(-7;-1) |
(-1;6) |
(6;+∞) |
| f’(x) |
- |
+ |
+ |
- |
2-й варіант
Функція у = f (x) диференційована. За даними, наведеними в таблиці, визначте проміжки зростання та спадання функції.
| x |
(-∞; -10) |
(-10;-2) |
(-2;9) |
(9;+∞) |
| f’(x) |
+ |
- |
+ |
+ |
Достатній рівень
1-й варіант
Знайдіть проміжки, на яких функція у= х3
– х2
– 5х – 3 спадає.
2-й варіант
Знайдіть проміжки, на яких функція у= х3
– х2
–х + 8 зростає.
Високий рівень
1-й варіант
Знайдіть, при яких значенях а функція
f (x) = 1/3 x3
– ½ ax2
+ 9x -3
зростає на R
2-й варіант
Знайдіть, при яких значенях а функція
f (x) = 1/3 x3
+ ½ ax2
+ 16x -3
Спадає на R.
Використання опорних конспектів і самостійних робіт дає змогу інтенсифікувати інформаційну діяльність викладача, досягти максимального засвоєння учнями навчального матеріалу безпосередньо на уроці.
Використання на уроках такого комплексу навчально-методичного забезпечення підвищує ефективність навчання , поглиблює і розширює знання учнів, стимулює їх творчу активність, урізноманітнює контроль.
Приділяють багато уваги роботі з одарованими учнями. Для цього викладач розробила комплекс завдань підвищеної складності , зокрема картки для самостійного розв’язування завдань.
Приклад картки
1. Знайти монотонності функцій :
a. у = - ¾ х4
+4х3
– 6х2
+ 5;
b. у = (х – 2)2
(х + 4)2
;
c. ( х – 2)2
/ (х+1)2
d. У = √х2
– 3х
2. Довести, що функція у = √2х – cosxзростає на всій числовій прямій.
3. Знайти проміжки монотонності функції ﴾π 2 / – х).
4. При яких значеннях а функція f (x) = ax3 + ax зростає на R.
5. Знайти всі значення параметра а, при яких функція f (x) = (a2 – 1) / 3x3 + (a – 1)x2 +2x+5 зростає на R
Щоб виявити переваги особисто орієнтованого навчання, серед учнів ліцею було проведене анкетування.
| № з/п |
Запитання |
Самооцінка учнів |
| 1 |
На уроках яких викладачів вам цікаво? |
| 2 |
Завдання з яких предметів ви виконуєте з інтересом (задоволеням) |
| 3 |
Хто з викладачів, на вашу думку, справедливо виставляє оцінки ? |
| 4 |
Творчі завдання з яких предметів ви виконували в цьому навчальному році? |
| 5 |
У кого з викладачів ви отримуєте грунтові знаня? |
| 6 |
Чи відчуваєте ви задоволення від навчання в ліцеї? |
| 7 |
Назвіть три предмети, яки вам подобають. Чому ? |
| 8 |
Чи уважно ви слухаєте поясненя викладача математики на уроках? |
| 9 |
Як, на вашу думку ,чи дає викладач на уроці багато додаткової інформації? |
| 10 |
Подобається вам відповідати усно біля дошки ? |
| 11 |
Чи любите ви відповідати з місця? |
| 12 |
Що внайбільше вам подобається вам із різних форм опитування :
· індивідуальний заклик
· контролююча самостійна робота
· усні відповіді на запитання
· письмова робота
· спільна робота в мікрогрупі?
|
| 13 |
Якщо буде контрольна робота з математики, чи покажете ви обрі знання? |
| 14 |
Чи списуєте ви під час контрольних робіт? |
| 15 |
Чи чекаєте ви уроків математики? |
| 16 |
Вас влаштовують оцінки, які вам виставляє викладач математики? |
| 17 |
Чи часто ви робите на уроках математики самоаналіз навчальних знань? |
| 18 |
Якщо вам щось незрозуміло, чи звертаєтесь ви до викладача? |
| 19 |
Як ви вважаєте , знання, які ви отримуєте на уроках математики, знадобляться вам у майбутньому? |
| 20 |
Чи відчуваєте ви в ліцеї творчу атмосферу ? |
| 21 |
Чи помічають педагоги, адміністрація ващі досягненя? |
Результати анкетування показали, що учням подобається працювати на уроках математики, самостійно та з допомогою викладача здобувати нові знання, оцінювати власні здобутки, що дає можливість познати особливості свого мислительного апарату, власних здібностей, професійної придатності та адаптації до соціальних процесів, які відбуваються у суспільстві.
Система методів роботи викладача математики спрямована не тільки на засвоєння компонентів змісту природничо-математичної освіти, а й на постійну та ефективну актуалізацію пізнавального, практичного, творчо-пошукового, морального ставлення учнів до дійності.
Література
1. Інноваційна діяльність №Н№. /Упоряд. Л. Галіцина – К.: Вид. дім «Шкіл. Світ» : Вид. Л. Галіцина, 2005.
2. Ващенко Л. Зміст і структура інноваційного педагогічного процессу // Директор школи . - № 2.
3. Методична служба – школі. Інформаційно-методичні матеріали на допомогу працівникам освіти. Випуск 1 / Укладачі : Ю.В. Буган, Г.Г. Свінних, В.І. Уруський. – Тернопіль : Астон 2003.
4. Методичні рекомендації для методичних служб ПТНЗ України / Укладач Н.І. Бугай – НМЦ ПТО МОН України, 2006
5. Передовий педагогічний досвід: теорія і методика / Під. Ред.. Л.Л. Момот / - К.: Рад. Шк. – 1990
6. Підласий І., Підласий А. Педагогічні іновації / Рад. Шк.. – 1998 - №12
7. Химинець В.В. Іоваціі у сучасній школі – Ужгород% Інформаційно-видавничий центр ЗІППО, 2004.
8. Шевчук С.С. Вивчення, узагальнення та впровадження передового педагогічного досвіду: Методичні рекомендації. – Донецьк, 2004
|