Случайные величины
Оглавление
Случайные величины.. 2
Функция распределения вероятностей.. 3
Основные свойства функции распределения вероятностей.. 5
Функция распределения вероятностей дискретной случайной величины6
Плотность распределения вероятностей.. 7
Плотность распределения вероятностей дискретной случайной величины9
Примеры плотностей и функций распределения вероятностей.. 10
Сингулярные случайные величины.. 13
Математическое ожидание случайной величины.. 15
Примеры вычисления математического ожидания случайной величины.. 17
Свойства математического ожидания. 19
Дисперсия случайной величины.. 20
Моменты случайной величины.. 22
Неравенство Чебышева. 23
Коэффициент асимметрии.. 25
Коэффициент эксцесса. 26
Среднеквадратическая ошибка. 27
Характеристическая функция. 28
Основные свойства характеристической функции.. 29
Примеры вычисления характеристической функции.. 30
Моменты, кумулянты и характеристическая функция. 31
Выше рассматривались эксперименты, результаты которых являются случайными событиями. Однако часто возникает необходимость количественного представления результатов эксперимента в виде некоторой величины  , которая называется случайной величиной. Случайная величина является вторым (после случайного события) основным объектом изучения теории вероятностей и обеспечивает более общий способ описания опыта со случайным исходом, чем совокупность случайных событий.
, которая называется случайной величиной. Случайная величина является вторым (после случайного события) основным объектом изучения теории вероятностей и обеспечивает более общий способ описания опыта со случайным исходом, чем совокупность случайных событий.
Рассматривая эксперименты со случайным исходом, мы уже имели дело со случайными величинами. Так, число успехов 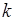 в серии из
в серии из 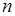 испытаний - пример случайной величины. Другими примерами случайных величин являются: число вызовов на телефонной станции за единицу времени; время ожидания очередного вызова; число частиц с заданной энергией в системах частиц, рассматриваемых в статистической физике; средняя суточная температура в данной местности и т.д.
испытаний - пример случайной величины. Другими примерами случайных величин являются: число вызовов на телефонной станции за единицу времени; время ожидания очередного вызова; число частиц с заданной энергией в системах частиц, рассматриваемых в статистической физике; средняя суточная температура в данной местности и т.д.
Случайная величина характерна тем, что невозможно точно предсказать ее значение, которое она примет, но с другой стороны, множество ее возможных значений обычно известно. Так для числа успехов в последовательности из 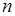 испытаний это множество конечно, поскольку число успехов может принимать значения
испытаний это множество конечно, поскольку число успехов может принимать значения 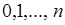 . Множество значений случайной величины, может совпадать с вещественной полуосью
. Множество значений случайной величины, может совпадать с вещественной полуосью 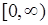 , как в случае времени ожидания и т.д.
, как в случае времени ожидания и т.д.
Реклама

Рассмотрим примеры экспериментов со случайным исходом, для описания которых обычно применяются случайные события и введем эквивалентное описание с помощью задания случайной величины.
1). Пусть результатом опыта может быть событие 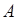 или событие
или событие 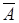 . Тогда этому эксперименту можно поставить в соответствие случайную величину
. Тогда этому эксперименту можно поставить в соответствие случайную величину  , которая принимает два значения, например,
, которая принимает два значения, например, 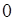 и
и 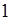 с вероятностями
с вероятностями 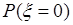 и
и 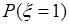 , причем имеют место равенства:
, причем имеют место равенства: 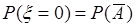 и
и 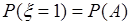 . Таким образом, опыт характеризуется двумя исходами
. Таким образом, опыт характеризуется двумя исходами 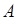 и
и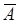 с вероятностями
с вероятностями 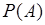 и
и 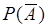 , или этот же опыт характеризуется случайной величиной
, или этот же опыт характеризуется случайной величиной  , принимающей два значения
, принимающей два значения 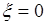 и
и 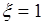 с вероятностями
с вероятностями 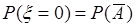 и
и 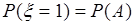 .
.
2). Рассмотрим опыт с бросанием игральной кости. Здесь исходом опыта может быть одно из событий 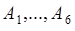 , где
, где 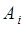 - выпадение грани с номером
- выпадение грани с номером 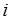 . Вероятности
. Вероятности 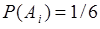 ,
, 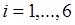 . Введем эквивалентное описание этого опыта с помощью случайной величины
. Введем эквивалентное описание этого опыта с помощью случайной величины  , которая может принимать значения
, которая может принимать значения 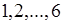 с вероятностями
с вероятностями 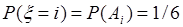 ,
, 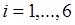 .
.
3). Последовательность 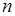 независимых испытаний характеризуется полной группой несовместных событий
независимых испытаний характеризуется полной группой несовместных событий 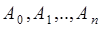 , где
, где 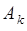 - событие, состоящее в появлении
- событие, состоящее в появлении 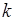 успехов в серии из
успехов в серии из 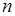 опытов; причем вероятность события
опытов; причем вероятность события 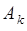 определяется формулой Бернули, т.е.
определяется формулой Бернули, т.е. 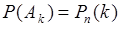 . Здесь можно ввести случайную величину
. Здесь можно ввести случайную величину  - число успехов, которая принимает значения
- число успехов, которая принимает значения 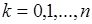 с вероятностями
с вероятностями 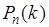 . Таким образом, последовательность независимых испытаний характеризуется случайными событиями
. Таким образом, последовательность независимых испытаний характеризуется случайными событиями 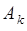 с их вероятностями
с их вероятностями 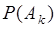 или случайной величиной
или случайной величиной  с вероятностями того, что
с вероятностями того, что  принимает значения
принимает значения 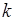 :
: 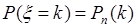 ,
, 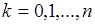 .
.
4). Однако, не для всякого опыта со случайным исходом существует столь простое соответствие между случайной величиной и совокупностью случайных событий. К примеру, рассмотрим эксперимент, в котором точка наугад бросается на отрезок 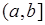 . Здесь естественно ввести случайную величину
. Здесь естественно ввести случайную величину  - координату на отрезке
- координату на отрезке 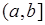 , в которую попадает точка. Таким образом, можно говорить о случайном событии
, в которую попадает точка. Таким образом, можно говорить о случайном событии 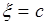 , где
, где 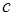 - число из
- число из 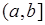 . Однако вероятность этого события
. Однако вероятность этого события 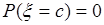 . Можно поступить иначе - отрезок
. Можно поступить иначе - отрезок 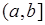 разбить на конечное число непересекающихся отрезков
разбить на конечное число непересекающихся отрезков 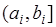 и рассматривать случайные события, состоящие в том, что случайная величина
и рассматривать случайные события, состоящие в том, что случайная величина  принимает значения из интервала
принимает значения из интервала 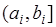 . Тогда вероятности
. Тогда вероятности 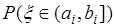 - конечные величины. Однако и этот способ имеет существенный недостаток, поскольку отрезки
- конечные величины. Однако и этот способ имеет существенный недостаток, поскольку отрезки 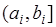 выбираются произвольным образом. Для того, чтобы устранить этот недостаток рассматривают отрезки вида
выбираются произвольным образом. Для того, чтобы устранить этот недостаток рассматривают отрезки вида 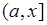 , где переменная
, где переменная 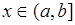 . Тогда соответствующая вероятность
. Тогда соответствующая вероятность
Реклама

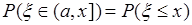 (29.1)
(29.1)
является функцией аргумента 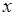 . Это усложняет математическое описание случайной величины, но при этом описание (29.1) становится единственным, устраняется неоднозначность выбора отрезков
. Это усложняет математическое описание случайной величины, но при этом описание (29.1) становится единственным, устраняется неоднозначность выбора отрезков 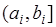 .
.
Для каждого из рассмотренных примеров несложно определить вероятностное пространство 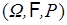 , где
, где 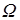 - пространство элементарных событий,
- пространство элементарных событий, 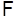 -
- 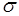 - алгебра событий (подмножеств
- алгебра событий (подмножеств 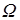 ),
), 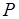 - вероятность, определенная для любого
- вероятность, определенная для любого 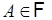 . Например, в последнем примере
. Например, в последнем примере 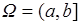 ,
, 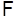 -
- 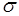 - алгебра всех отрезков
- алгебра всех отрезков 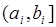 , содержащихся в
, содержащихся в 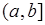 .
.
Рассмотренные примеры приводят к следующему определению случайной величины.
Пусть 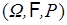 - вероятностное пространство. Случайной величиной
- вероятностное пространство. Случайной величиной  называется однозначная действительная функция
называется однозначная действительная функция 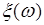 , определенная на
, определенная на 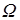 , для которой множество элементарных событий вида
, для которой множество элементарных событий вида 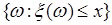 является событием (т.е. принадлежат
является событием (т.е. принадлежат 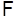 ) для каждого действительного числа
) для каждого действительного числа 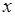 .
.
Таким образом, в определении требуется, чтобы для каждого вещественного 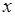 множество
множество 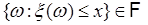 , и это условие гарантирует, что для каждого
, и это условие гарантирует, что для каждого 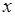 определена вероятность события
определена вероятность события 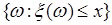 . Это событие принято обозначать более краткой записью
. Это событие принято обозначать более краткой записью 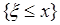 .
.
Функция
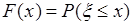 ,
, 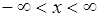 , (30.1)
, (30.1)
называется функцией распределения вероятностей случайной величины  .
.
Функция 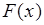 иногда называется кратко – функция распределения, а также – интегральным законом распределения вероятностей случайной величины
иногда называется кратко – функция распределения, а также – интегральным законом распределения вероятностей случайной величины  . Функция
. Функция 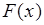 является полной характеристикой случайной величины, то есть представляет собой математическое описание всех свойств случайной величины и более детального способа описания этих свойств не существует.
является полной характеристикой случайной величины, то есть представляет собой математическое описание всех свойств случайной величины и более детального способа описания этих свойств не существует.
Отметим следующую важную особенность определения (30.1). Часто функцию 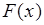 определяют иначе:
определяют иначе:
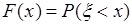 ,
, 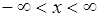 . (30.2)
. (30.2)
Согласно (30.1) функция 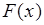 является непрерывной справа. Этот вопрос подробнее будет рассмотрен ниже. Если же использовать определение (30.2), то
является непрерывной справа. Этот вопрос подробнее будет рассмотрен ниже. Если же использовать определение (30.2), то 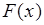 - непрерывна слева, что является следствием применения строгого неравенства в соотношении (30.2). Функции (30.1) и (30.2) представляют собой эквивалентные описания случайной величины, поскольку не имеет значения каким определением пользоваться как при изучении теоретических вопросов, так и при решении задач. Для определенности в дальнейшем будем использовать только определение (30.1).
- непрерывна слева, что является следствием применения строгого неравенства в соотношении (30.2). Функции (30.1) и (30.2) представляют собой эквивалентные описания случайной величины, поскольку не имеет значения каким определением пользоваться как при изучении теоретических вопросов, так и при решении задач. Для определенности в дальнейшем будем использовать только определение (30.1).
Рассмотрим пример построения графика функции 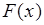 . Пусть случайная величина
. Пусть случайная величина  принимает значения
принимает значения 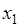 ,
, 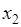 ,
, 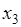 с вероятностями
с вероятностями 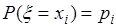 ,
,  , причем
, причем 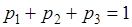 . Таким образом, другие значения кроме указанных данная случайная величина принимает с нулевой вероятностью:
. Таким образом, другие значения кроме указанных данная случайная величина принимает с нулевой вероятностью: 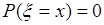 , для любого
, для любого 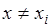 ,
,  . Или как говорят, других значений кроме
. Или как говорят, других значений кроме 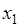 ,
, 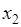 ,
, 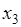 случайная величина
случайная величина  не может принимать. Пусть для определенности
не может принимать. Пусть для определенности 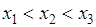 . Найдем значения функции
. Найдем значения функции 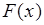 для
для 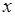 из интервалов: 1)
из интервалов: 1) 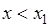 , 2)
, 2) 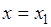 , 3)
, 3) 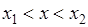 , 4)
, 4) 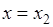 , 5)
, 5) 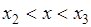 , 6)
, 6) 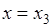 , 7)
, 7) 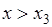 . На первом интервале
. На первом интервале 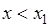 , поэтому функция распределения
, поэтому функция распределения 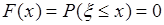 . 2). Если
. 2). Если 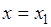 , то
, то 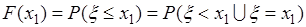 . Очевидно случайные события
. Очевидно случайные события 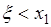 и
и 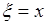 несовместны, поэтому по формуле сложения вероятностей
несовместны, поэтому по формуле сложения вероятностей 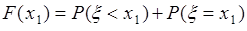 . По условию событие
. По условию событие 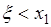 невозможное и
невозможное и 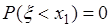 , а
, а 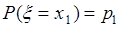 . Поэтому
. Поэтому 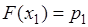 . 3). Пусть
. 3). Пусть 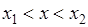 , тогда
, тогда 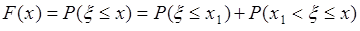 . Здесь первое слагаемое
. Здесь первое слагаемое 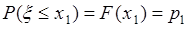 , а второе
, а второе 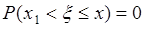 , поскольку событие
, поскольку событие 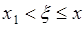 - невозможное. Таким образом
- невозможное. Таким образом 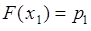 для любого
для любого 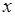 , удовлетворяющего условию
, удовлетворяющего условию 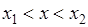 . 4). Пусть
. 4). Пусть 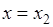 , тогда
, тогда 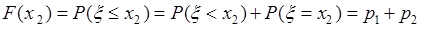 . 5). Если
. 5). Если 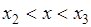 , то
, то 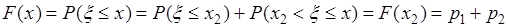 . 6) При
. 6) При 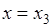 имеем
имеем 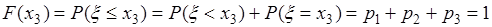 . 7) Если
. 7) Если 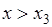 , то
, то 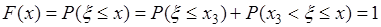 . Результаты вычислений представлены на рис. 30.1 графиком функции
. Результаты вычислений представлены на рис. 30.1 графиком функции 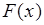 . В точках разрыва
. В точках разрыва 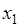 ,
, 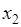 ,
, 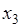 указана непрерывность функции справа.
указана непрерывность функции справа.
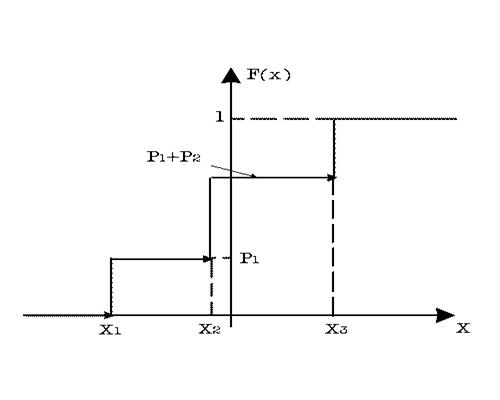
Рис. 30.1. График функции распределения вероятностей.
Рассмотрим основные свойства функции распределения, следующие непосредственно из определения:
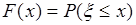 . (31.1)
. (31.1)
1. Введем обозначение: 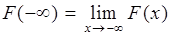 . Тогда из определения следует
. Тогда из определения следует 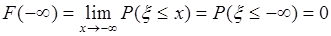 . Здесь выражение
. Здесь выражение 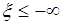 рассматривается как невозможное событие с нулевой вероятностью.
рассматривается как невозможное событие с нулевой вероятностью.
2. Пусть 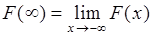 . Тогда из определения функции
. Тогда из определения функции 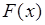 следует
следует 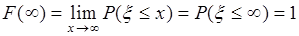 . Случайное событие
. Случайное событие 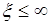 является достоверным и его вероятность равна единице.
является достоверным и его вероятность равна единице.
3. Вероятность 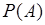 случайного события
случайного события 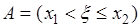 , состоящего в том, что случайная величина
, состоящего в том, что случайная величина  принимает значение из интервала
принимает значение из интервала 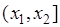 при
при 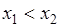 определяется через функцию
определяется через функцию 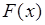 следующим равенством
следующим равенством
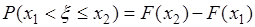 . (31.2)
. (31.2)
Для доказательства этого равенства рассмотрим соотношение
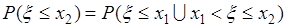 . (31.3)
. (31.3)
События 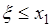 и
и 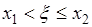 несовместны, поэтому по формуле сложения вероятностей из (31.3) следует
несовместны, поэтому по формуле сложения вероятностей из (31.3) следует
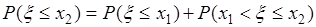 , (31.4)
, (31.4)
что и совпадает с формулой (31.2), поскольку 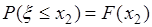 и
и 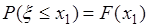 .
.
4. Функция 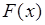 является неубывающей. Для доказательства рассмотрим
является неубывающей. Для доказательства рассмотрим 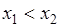 . При этом справедливо равенство (31.2). Его левая часть
. При этом справедливо равенство (31.2). Его левая часть 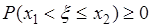 , поскольку вероятность принимает значения из интервала
, поскольку вероятность принимает значения из интервала 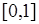 . Поэтому и правая часть равенства (31.2) неотрицательна:
. Поэтому и правая часть равенства (31.2) неотрицательна: 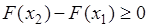 , или
, или 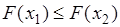 . Это равенство получено при условии
. Это равенство получено при условии 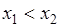 , поэтому
, поэтому 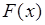 - неубывающая функция.
- неубывающая функция.
5. Функция 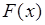 непрерывна справа в каждой точке
непрерывна справа в каждой точке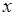 , т.е.
, т.е.
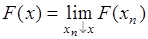 , (31.5)
, (31.5)
где 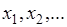 - любая последовательность, стремящаяся к
- любая последовательность, стремящаяся к 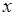 справа, т.е.
справа, т.е. 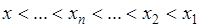 и
и 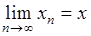 .
.
Для доказательства представим функцию 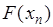 в виде:
в виде: 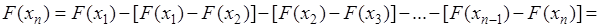
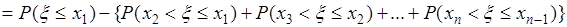 . (31.5)
. (31.5)
Отсюда
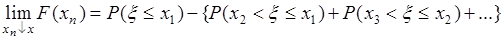 . (31.6)
. (31.6)
Теперь на основании аксиомы счетной аддитивности вероятности выражение в фигурных скобках равно 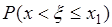 , таким образом
, таким образом 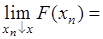
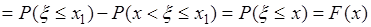 , что и доказывает непрерывность справа функции
, что и доказывает непрерывность справа функции 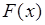 .
.
Таким образом, каждая функция распределения вероятностей обладает свойствами 1-5. Верно и обратное утверждение: если 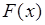 ,
, 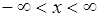 , удовлетворяет условиям 1-5 ,то она может рассматриваться как функция распределения некоторой случайной величины.
, удовлетворяет условиям 1-5 ,то она может рассматриваться как функция распределения некоторой случайной величины.
Случайная величина  называется дискретной, если множество ее значений конечно или счетно.
называется дискретной, если множество ее значений конечно или счетно.
Для полного вероятностного описания дискретной случайной величины  , принимающей значения
, принимающей значения 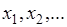 , достаточно задать вероятности
, достаточно задать вероятности
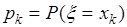 ,
, 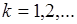 (32.1)
(32.1)
того, что случайная величина  принимает значение
принимает значение 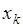 . Если заданы
. Если заданы 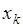 и
и 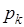 ,
, 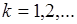 , тогда функцию распределения вероятностей
, тогда функцию распределения вероятностей 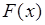 дискретной случайной величины
дискретной случайной величины  можно представить в виде:
можно представить в виде:
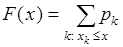 . (32.2)
. (32.2)
Здесь суммирование ведется по всем индексам 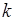 , удовлетворяющим условию:
, удовлетворяющим условию: 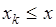 .
.
Функцию распределения вероятностей дискретной случайной величины иногда представляют через так называемую функцию единичного скачка
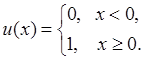 (32.3)
(32.3)
При этом 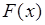 принимает вид
принимает вид
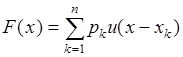 , (32.4)
, (32.4)
если случайная величина  принимает конечное множество значений
принимает конечное множество значений 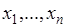 , и верхний предел суммирования в (32.4) полагается равным
, и верхний предел суммирования в (32.4) полагается равным 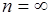 , если случайная величина принимает счетное множество значений.
, если случайная величина принимает счетное множество значений.
Пример построения графика функций распределения вероятностей дискретной случайной величины был рассмотрен в п.30.
Пусть случайная величина  имеет дифференцируемую функцию распределению вероятностей
имеет дифференцируемую функцию распределению вероятностей 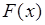 , тогда функция
, тогда функция
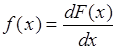 (33.1)
(33.1)
называется плотностью распределения вероятностей ( или плотностью вероятности) случайной величины  , а случайная величина
, а случайная величина  - непрерывной случайной величиной.
- непрерывной случайной величиной.
Рассмотрим основные свойства плотности вероятности.
Из определения производной следует равенство:
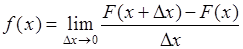 . (33.2)
. (33.2)
Согласно свойствам функции 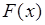 имеет место равенство
имеет место равенство 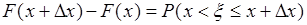 . Поэтому (33.2) принимает вид:
. Поэтому (33.2) принимает вид:
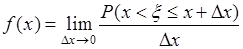 . (33.3)
. (33.3)
Это соотношение объясняет название функции 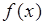 . Действительно, согласно (33.3) функция
. Действительно, согласно (33.3) функция 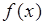 - это вероятность
- это вероятность 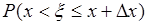 , приходящаяся на единицу интервала
, приходящаяся на единицу интервала 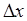 , в точке
, в точке 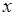 , поскольку
, поскольку 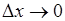 . Таким образом, плотность вероятности, определяемая соотношением (33.3), аналогична определениям плотностей других величин, известных в физике, таких как плотность тока, плотность вещества, плотность заряда и т.д.
. Таким образом, плотность вероятности, определяемая соотношением (33.3), аналогична определениям плотностей других величин, известных в физике, таких как плотность тока, плотность вещества, плотность заряда и т.д.
2. Поскольку 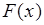 - неубывающая функция, то ее производная
- неубывающая функция, то ее производная 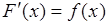 - функция неотрицательная:
- функция неотрицательная:
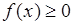 . (33.4)
. (33.4)
3. Из (33.1) следует
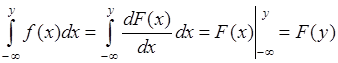 ,
,
поскольку 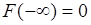 . Таким образом, справедливо равенство
. Таким образом, справедливо равенство
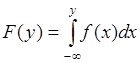 . (33.5)
. (33.5)
4. Поскольку 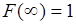 , то из соотношения (33.5) следует
, то из соотношения (33.5) следует
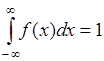 (33.6)
(33.6)
- равенство, которое называется условием нормировки. Его левая часть 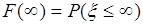 - это вероятность достоверного события.
- это вероятность достоверного события.
5. Пусть 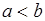 , тогда из (33.1) следует
, тогда из (33.1) следует
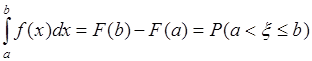 . (33.7)
. (33.7)
Это соотношение имеет важное значение для приложений, поскольку позволяет вычислить вероятность 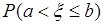 через плотность вероятности
через плотность вероятности 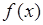 или через функцию распределения вероятностей
или через функцию распределения вероятностей 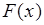 . Если положить
. Если положить 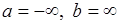 , то из (33.7) следует соотношение (33.6).
, то из (33.7) следует соотношение (33.6).
На рис. 33.1 представлены примеры графиков функции распределения и плотности вероятностей.
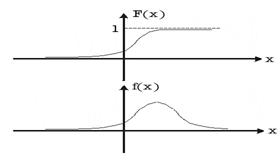
Рис. 33.1. Примеры функции распределения вероятностей и плотности вероятности.
Отметим, что плотность распределения вероятности может иметь несколько максимумов. Значение 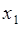 аргумента
аргумента 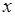 , при котором плотность
, при котором плотность 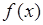 имеет максимум называется модой распределения случайной величины
имеет максимум называется модой распределения случайной величины  . Если плотность
. Если плотность 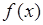 имеет более одной моды, то
имеет более одной моды, то 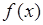 называется многомодальной.
называется многомодальной.
Пусть случайная величина  принимает значения
принимает значения 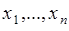 с вероятностями
с вероятностями 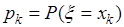 ,
, 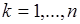 . Тогда ее функция распределения вероятностей
. Тогда ее функция распределения вероятностей
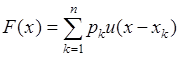 , (34.1)
, (34.1)
где 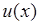 - функция единичного скачка. Определить плотность вероятности
- функция единичного скачка. Определить плотность вероятности 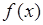 случайной величины
случайной величины  по ее функции распределения
по ее функции распределения 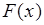 можно с учетом равенства
можно с учетом равенства 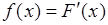 . Однако при этом возникают математические сложности, связанные с тем, что функция единичного скачка
. Однако при этом возникают математические сложности, связанные с тем, что функция единичного скачка 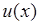 , входящая в (34.1), имеет разрыв первого рода при
, входящая в (34.1), имеет разрыв первого рода при 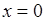 . Поэтому в точке
. Поэтому в точке 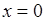 не существует производная
не существует производная 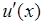 функции
функции 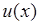 .
.
Для преодоления этой сложности вводится 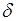 -функция. Функцию единичного скачка можно представить через
-функция. Функцию единичного скачка можно представить через 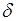 -функцию следующим равенством:
-функцию следующим равенством:
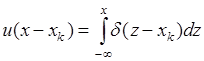 . (34.2)
. (34.2)
Тогда формально производная
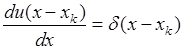 (34.3)
(34.3)
и плотность вероятности дискретной случайной величины определяется из соотношения (34.1) как производная функции 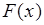 :
:
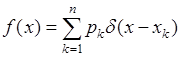 . (34.4)
. (34.4)
Функция (34.4) обладает всеми свойствами плотности вероятности. Рассмотрим пример. Пусть дискретная случайная величина  принимает значения
принимает значения 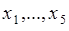 с вероятностями
с вероятностями 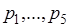 , и пусть
, и пусть 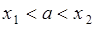 ,
, 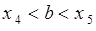 . Тогда вероятность
. Тогда вероятность 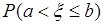 - того, что случайная величина
- того, что случайная величина  примет значение из отрезка
примет значение из отрезка 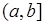 может быть вычислена, исходя из общих свойств плотности по формуле:
может быть вычислена, исходя из общих свойств плотности по формуле:
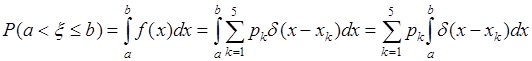 .
.
Здесь
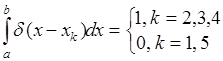 ,
,
поскольку особая точка 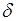 - функции, определяемая условием
- функции, определяемая условием 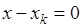 , находится внутри области интегрирования при
, находится внутри области интегрирования при 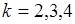 , а при
, а при 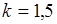 особая точка находится вне области интегрирования. Таким образом,
особая точка находится вне области интегрирования. Таким образом,
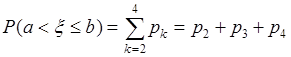 .
.
Для функции (34.4) также выполняется условие нормировки:
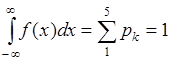 .
.
Отметим, что в математике запись вида (34.4) считается некорректной (неправильной), а запись (34.2) - корректной. Это обусловлено тем, что 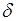 -функция при нулевом аргументе
-функция при нулевом аргументе 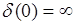 , и говорят, что
, и говорят, что 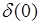 не существует. С другой стороны, в (34.2)
не существует. С другой стороны, в (34.2) 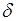 -функция содержится под интегралом. При этом правая часть (34.2) - конечная величина для любого
-функция содержится под интегралом. При этом правая часть (34.2) - конечная величина для любого 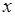 , т.е. интеграл от
, т.е. интеграл от 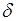 -функции существует. Несмотря на это в физике, технике и других приложениях теории вероятностей часто используется представление плотности в виде (34.4), которое, во-первых, позволяет получать верные результаты, применяя свойства
-функции существует. Несмотря на это в физике, технике и других приложениях теории вероятностей часто используется представление плотности в виде (34.4), которое, во-первых, позволяет получать верные результаты, применяя свойства 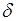 - функции, и во-вторых, имеет очевидную физическую интерпретацию.
- функции, и во-вторых, имеет очевидную физическую интерпретацию.
35.1.
Случайная величина  называется равномерно распределенной на отрезке
называется равномерно распределенной на отрезке 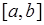 , если ее плотность распределения вероятностей
, если ее плотность распределения вероятностей
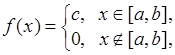 (35.1)
(35.1)
где 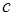 - число, определяемое из условия нормировки:
- число, определяемое из условия нормировки:
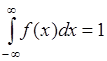 . (35.2)
. (35.2)
Подстановка (35.1) в (35.2) приводит к равенству, решение которого относительно 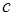 имеет вид:
имеет вид: 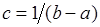 .
.
Функция распределения вероятностей 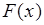 равномерно распределенной случайной величины может быть найдена по формуле (33.5), определяющей
равномерно распределенной случайной величины может быть найдена по формуле (33.5), определяющей 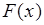 через плотность:
через плотность:
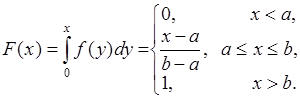 (35.3)
(35.3)
На рис. 35.1 представлены графики функций 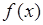 и
и 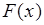 равномерно распределенной случайной величины.
равномерно распределенной случайной величины.
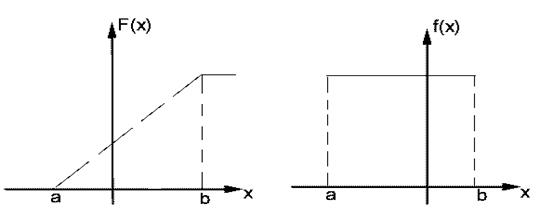
Рис. 35.1. Графики функции и плотности распределения
равномерно распределенной случайной величины.
35.2.
Случайная величина  называется нормальной (или гауссовой), если ее плотность распределения вероятностей:
называется нормальной (или гауссовой), если ее плотность распределения вероятностей:
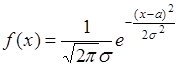 , (35.4)
, (35.4)
где 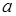 ,
, 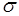 - числа, называемые параметрами функции
- числа, называемые параметрами функции 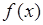 . При
. При 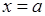 функция
функция 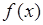 принимает свое максимальное значение:
принимает свое максимальное значение: 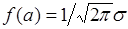 . Параметр
. Параметр 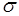 имеет смысл эффективной ширины
имеет смысл эффективной ширины 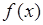 . Кроме этой геометрической интерпретации параметры
. Кроме этой геометрической интерпретации параметры 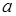 ,
, 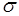 имеют и вероятностную трактовку, которая будет рассмотрена в последующем.
имеют и вероятностную трактовку, которая будет рассмотрена в последующем.
Из (35.4) следует выражение для функции распределения вероятностей
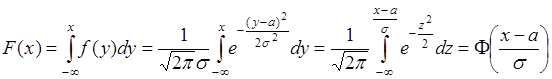 , (35.5)
, (35.5)
где 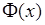 - функция Лапласа. На рис. 35.2 представлены графики функций
- функция Лапласа. На рис. 35.2 представлены графики функций 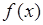 и
и 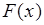 нормальной случайной величины. Для обозначения того, что случайная величина
нормальной случайной величины. Для обозначения того, что случайная величина  имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 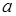 и
и 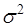 часто используется запись
часто используется запись 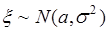 .
.
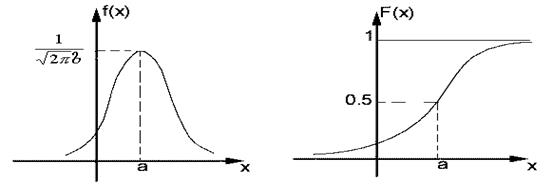
Рис. 35.2. Графики плотности и функции распределения
нормальной случайной величины.
35.3.
Случайная величина  имеет плотность распределения вероятностей Коши, если
имеет плотность распределения вероятностей Коши, если
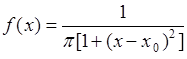 . (35.6)
. (35.6)
Этой плотности соответствует функция распределения
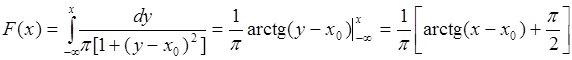 .
.
(35.7)
35.4.
Случайная величина  называется распределенной по экспоненциальному закону, если ее плотность распределения вероятностей имеет вид:
называется распределенной по экспоненциальному закону, если ее плотность распределения вероятностей имеет вид:
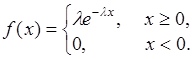 (35.8)
(35.8)
Определим ее функцию распределения вероятностей. При 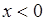 из (35.8) следует
из (35.8) следует 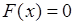 . Если
. Если 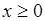 , то
, то
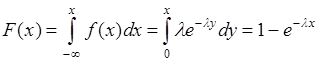 . (35.9)
. (35.9)
35.5.
Релеевское распределение вероятностей случайной величины определяется плотностью вида
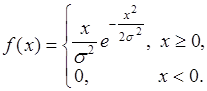 (35.10)
(35.10)
Этой плотности соответствует функция распределения вероятностей 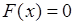 при
при 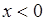 и равная
и равная
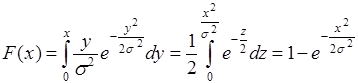 (35.11)
(35.11)
при 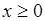 .
.
35.6.
Рассмотрим примеры построения функции распределения и плотности дискретной случайной величины. Пусть случайная величина  - это число успехов в последовательности из
- это число успехов в последовательности из 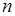 независимых испытаний. Тогда случайная величина
независимых испытаний. Тогда случайная величина  принимает значения
принимает значения 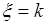 ,
, 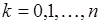 с вероятностью
с вероятностью 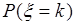 , которая определяется формулой Бернулли:
, которая определяется формулой Бернулли:
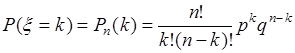 , (35.12)
, (35.12)
где 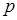 ,
, 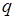 - вероятности успеха и неуспеха в одном опыте. Таким образом, функция распределения вероятностей случайной величины
- вероятности успеха и неуспеха в одном опыте. Таким образом, функция распределения вероятностей случайной величины  имеет вид
имеет вид
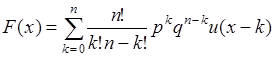 , (35.13)
, (35.13)
где 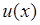 - функция единичного скачка. Отсюда плотность распределения:
- функция единичного скачка. Отсюда плотность распределения:
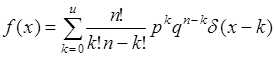 , (35.14)
, (35.14)
где 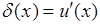 - дельта-функция.
- дельта-функция.
Кроме дискретных и непрерывных случайных величин существуют еще так называемые сингулярные случайные величины. Эти случайные величины характеризуются тем, что их функция распределения вероятностей 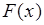 - непрерывна, но точки роста
- непрерывна, но точки роста 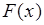 образуют множество нулевой меры. Точкой роста
образуют множество нулевой меры. Точкой роста 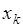 функции
функции 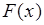 называется значение ее аргумента
называется значение ее аргумента 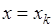 такое, что производная
такое, что производная 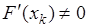 .
.
Таким образом, 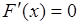 почти всюду на области определения функции. Функцию
почти всюду на области определения функции. Функцию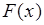 , удовлетворяющую этому условию, также называют сингулярной. Примером сингулярной функции распределения является кривая Кантора (рис. 36.1), которая строится следующим образом. Полагается
, удовлетворяющую этому условию, также называют сингулярной. Примером сингулярной функции распределения является кривая Кантора (рис. 36.1), которая строится следующим образом. Полагается 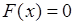 при
при 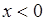 и
и 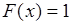 при
при  . Затем интервал
. Затем интервал 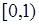 разбивается на три равных части (сегмента) и для внутреннего сегмента
разбивается на три равных части (сегмента) и для внутреннего сегмента 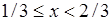 определяется значение
определяется значение 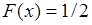 - как полусумма уже определенных значений на ближайших сегментах справа и слева. На данный момент функция
- как полусумма уже определенных значений на ближайших сегментах справа и слева. На данный момент функция 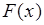 определена для
определена для 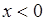 , ее значение
, ее значение 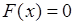 , и для
, и для  со значением
со значением 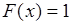 . Полусумма этих значений равна
. Полусумма этих значений равна 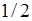 и определяет значение
и определяет значение 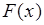 на внутреннем сегменте
на внутреннем сегменте 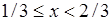 . Затем рассматриваются отрезки
. Затем рассматриваются отрезки
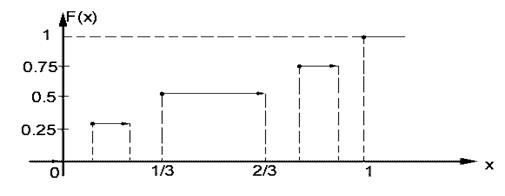
Рис. 36.1. Построение кривой Кантора.
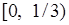 и
и 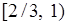 , каждый из них разбивается на три равных сегмента и функция
, каждый из них разбивается на три равных сегмента и функция 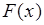 определяется на внутренних сегментах как полусумма ближайших справа и слева заданных значений функции
определяется на внутренних сегментах как полусумма ближайших справа и слева заданных значений функции 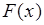 . Таким образом, при
. Таким образом, при 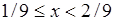 функция
функция 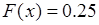 - как полусумма чисел
- как полусумма чисел 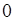 и
и 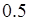 . Аналогично на интервале
. Аналогично на интервале 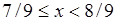 функция
функция 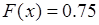 . Затем функция
. Затем функция 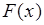 определяется на интервале
определяется на интервале 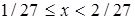 , на котором
, на котором 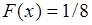 и т.д.
и т.д.
Суммарная длина всех внутренних сегментов равна
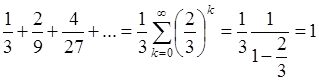
Поэтому, рассматривая интервал 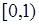 , говорят что функция
, говорят что функция 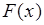 - постоянная на множестве меры 1, на множестве меры 0 растет, но без скачков.
- постоянная на множестве меры 1, на множестве меры 0 растет, но без скачков.
Известна теорема Лебега. Любая функция распределения 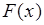 может быть единственным образом представлена в виде суммы трех компонент: дискретной, непрерывной и сингулярной.
может быть единственным образом представлена в виде суммы трех компонент: дискретной, непрерывной и сингулярной.
Сингулярные распределения практически не встречаются в реальных задачах и поэтому исключаются из нашего дальнейшего изучения.
37.1. Функция распределения вероятностей или плотность вероятности являются полными вероятностными характеристиками случайной величины. Однако, во многих задачах такая полная характеристика случайной величины, с одной стороны, может быть неизвестна для исследователя, а с другой стороны и не обязательна, достаточно ограничиться значением некоторых параметров распределения вероятностей, т.е. некоторых чисел (или числовых характеристик). Здесь уместна аналогия с геометрическим описанием сложной формы твердого тела, когда ограничиваются такими характеристиками (числами) как длина, ширина, высота, объем, момент инерции, и т.д., а детальное описание сложной формы этого тела не рассматривается. Числовыми характеристиками случайных величин чаще всего служат так называемые моменты распределения, простейшим из которых является математическое ожидание случайной величины.
Прежде чем вводить определение математического ожидания случайной величины, рассмотрим выражение среднего арифметического результатов измерения дискретной случайной величины. Пусть случайная величина  может принимать значения
может принимать значения 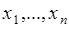 соответственно с вероятностями
соответственно с вероятностями 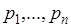 . Результат измерения случайной величины
. Результат измерения случайной величины  в каждом опыте - это одно из чисел
в каждом опыте - это одно из чисел 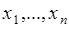 . Пусть выполнено
. Пусть выполнено 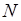 опытов, среди них в
опытов, среди них в 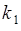 опытах случайная величина
опытах случайная величина  принимала значение
принимала значение 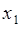 , в
, в 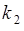 опытах - значение
опытах - значение 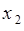 ,..., в
,..., в 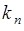 опытах - значение
опытах - значение 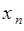 . Очевидно,
. Очевидно, 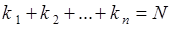 - полное число опытов. Пусть
- полное число опытов. Пусть 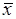 - среднее арифметическое результатов измерения случайной величины
- среднее арифметическое результатов измерения случайной величины  в
в 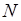 опытах, тогда
опытах, тогда
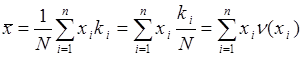 , (37.1)
, (37.1)
где 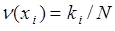 - частота появления числа
- частота появления числа 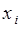 при измерении случайной величины
при измерении случайной величины  в
в 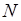 опытах. С увеличением числа опытов
опытах. С увеличением числа опытов 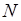 величина
величина 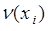 приближается к числу
приближается к числу 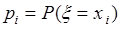 . Поэтому для того, чтобы определить теоретический аналог среднего арифметического
. Поэтому для того, чтобы определить теоретический аналог среднего арифметического 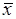 достаточно в формуле (37.1) частоту
достаточно в формуле (37.1) частоту 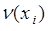 заменить на вероятность
заменить на вероятность 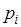 . Это приводит к следующему определению.
. Это приводит к следующему определению.
Математическим ожиданием (средним, статистическим средним) дискретной случайной величины  , принимающей значения
, принимающей значения 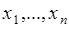 с вероятностями
с вероятностями 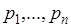 , называется число
, называется число
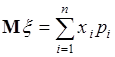 . (37.2)
. (37.2)
Если множество значений дискретной случайной величины счетно: 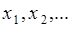 , то в (37.2) полагается
, то в (37.2) полагается 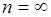 .
.
Пусть 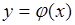 - однозначная функция одной переменной,
- однозначная функция одной переменной,  - дискретная случайная величина, принимающая значения
- дискретная случайная величина, принимающая значения 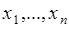 с вероятностями
с вероятностями 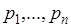 . Тогда
. Тогда 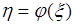 - дискретная случайная величина, принимающая значения
- дискретная случайная величина, принимающая значения 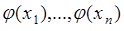 с вероятностями
с вероятностями 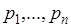 . Поэтому из определения (37.2) математического ожидания следует
. Поэтому из определения (37.2) математического ожидания следует
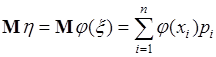 (37.3)
(37.3)
- выражение, определяющее математическое ожидание функции 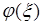 .
.
Математическим ожиданием непрерывной случайной величины  с плотностью распределения вероятностей
с плотностью распределения вероятностей 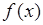 называется число
называется число
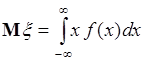 . (37.4)
. (37.4)
Аналогично определяется математическое ожидание случайной величины 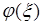 - как число
- как число
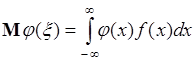 , (37.5)
, (37.5)
где 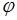 - однозначная функция одной переменной,
- однозначная функция одной переменной, 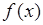 - плотность распределения вероятностей случайной величины
- плотность распределения вероятностей случайной величины  .
.
37.2. Определения (37.2) и (37.4) согласуются друг с другом. Соотношение (37.4) можно представить приближенно в виде интегральной суммы:
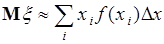 , (37.6)
, (37.6)
где 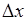 - малая величина. Тогда
- малая величина. Тогда 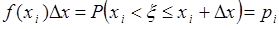 , и следовательно, (37.4) формально представимо суммой (37.2).
, и следовательно, (37.4) формально представимо суммой (37.2).
Если  - дискретная величина, принимающая значения
- дискретная величина, принимающая значения 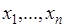 с вероятностями
с вероятностями 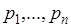 , то ее плотность вероятности
, то ее плотность вероятности 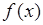 можно представить через
можно представить через 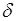 - функцию:
- функцию:
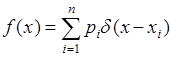 . (37.7)
. (37.7)
Подставим (37.7) в (37.4), тогда
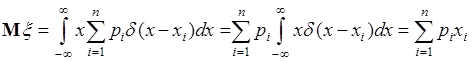 , (37.8)
, (37.8)
что совпадает с (37.2). Таким образом, определение (37.4) математического ожидания можно использовать как универсальное определение как для непрерывных, так и для дискретных случайных величин. Однако вычислять математическое ожидание дискретной случайной величины, конечно, удобнее по формуле (37.2).
Выражение (37.4) можно представить через функцию распределения 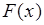 случайной величины
случайной величины  . Для этого выполним следующие преобразования:
. Для этого выполним следующие преобразования: 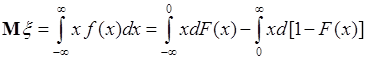 . Далее используем для вычисления интеграла способ «по частям»:
. Далее используем для вычисления интеграла способ «по частям»:
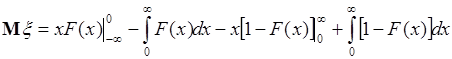 .
.
Пусть функция 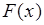 удовлетворяет условиям:
удовлетворяет условиям: 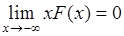 ,
, 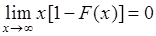 , тогда
, тогда
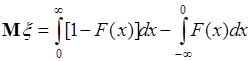 . (37.9)
. (37.9)
Это выражение позволяет вычислять математическое ожидание 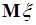 через функцию распределения
через функцию распределения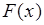 .
.
38.1. Пусть гауссова случайная величина  имеет плотность распределения вероятностей (35.4). Вычислим ее математическое ожидание. Для этого подставим выражение (35.4) в формулу (37.4), тогда
имеет плотность распределения вероятностей (35.4). Вычислим ее математическое ожидание. Для этого подставим выражение (35.4) в формулу (37.4), тогда
 . (38.1)
. (38.1)
Вместо переменной интегрирования 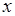 введем новую переменную
введем новую переменную 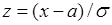 ,
, 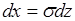 , тогда
, тогда
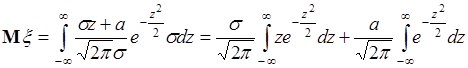 . (38.2)
. (38.2)
Функция 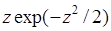 является нечетной, поэтому интеграл в первом слагаемом (38.2) равен нулю. Во втором слагаемом
является нечетной, поэтому интеграл в первом слагаемом (38.2) равен нулю. Во втором слагаемом
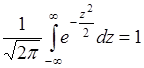 . (38.3)
. (38.3)
Это равенство представляет собой условие нормировки для гауссовой плотности распределения вероятностей (35.4) с параметрами: 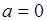 и
и 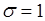 . Таким образом, из (38.2) следует
. Таким образом, из (38.2) следует 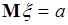 - среднее гауссовой случайной величины является параметром плотности распределения вероятностей (35.4). В данном случае
- среднее гауссовой случайной величины является параметром плотности распределения вероятностей (35.4). В данном случае 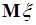 имеет геометрическую интерпретацию (рис. 35.2) как значение аргумента
имеет геометрическую интерпретацию (рис. 35.2) как значение аргумента 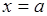 , при котором плотность (35.4) принимает максимальное значение. В дальнейшем символ
, при котором плотность (35.4) принимает максимальное значение. В дальнейшем символ 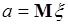 используется также и для обозначения среднего любой случайной величины
используется также и для обозначения среднего любой случайной величины  .
.
38.2. Вычислим среднее случайной величины  , распределенной по экспоненциальному закону (35.8):
, распределенной по экспоненциальному закону (35.8):
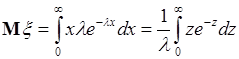 . (38.4)
. (38.4)
Далее используем способ интегрирования «по частям»:
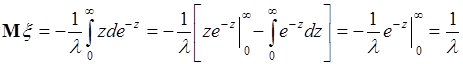 . (38.5)
. (38.5)
38.3. Пусть  - число успехов в серии из
- число успехов в серии из 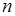 независимых опытов. Тогда вероятности
независимых опытов. Тогда вероятности 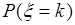 ,
, 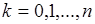 определяются формулой Бернули. Поэтому
определяются формулой Бернули. Поэтому
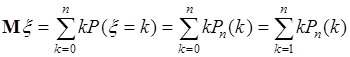 . (38.6)
. (38.6)
Последнее равенство справедливо, поскольку 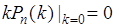 . Подставим в (38.6) формулу Бернули, тогда:
. Подставим в (38.6) формулу Бернули, тогда:
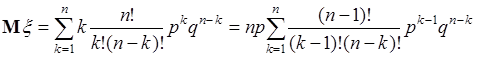 . (38.7)
. (38.7)
Введем новый индекс суммирования 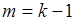 , тогда
, тогда
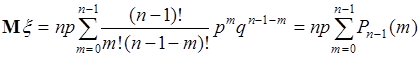 . (38.8)
. (38.8)
Поскольку 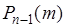 - вероятность
- вероятность 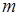 успехов в серии из
успехов в серии из 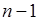 опытов, то
опытов, то 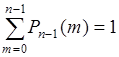 - как вероятность достоверного события, состоящего в появлении любого числа успехов в интервале
- как вероятность достоверного события, состоящего в появлении любого числа успехов в интервале 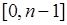 . Поэтому из (38.8) следует
. Поэтому из (38.8) следует
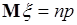 . (38.9)
. (38.9)
38.4.
Однако не у всякой случайной величины существует ее математическое ожидание. Причиной этого является расходимость интеграла (37.4), что в свою очередь, обусловлено малой скоростью сходимости к нулю плотности 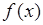 при
при 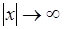 , так что для функции
, так что для функции 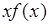 не существует интеграл вида (37.4). Для примера рассмотрим вычисление математического ожидания случайной величины
не существует интеграл вида (37.4). Для примера рассмотрим вычисление математического ожидания случайной величины  , распределенной по закону Коши:
, распределенной по закону Коши: 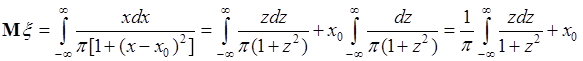 .
.
(
38.10)
Здесь несобственный интеграл расходится, так как
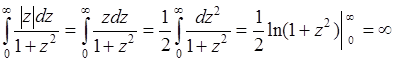 .
.
Следовательно, случайная величина  не имеет математического ожидания. Однако, если интеграл в (38.10) понимать в смысле главного значения Коши, то
не имеет математического ожидания. Однако, если интеграл в (38.10) понимать в смысле главного значения Коши, то
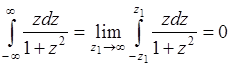 ,
,
поскольку функция 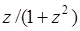 является нечетной. Следовательно, при этом
является нечетной. Следовательно, при этом
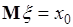 . (38.11)
. (38.11)
Основные свойства математического ожидания следуют непосредственно из свойств интеграла в определении (37.5):
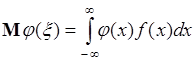 . (39.1)
. (39.1)
1. Пусть 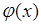 представляет собой постоянную
представляет собой постоянную 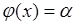 , тогда из (39.1) следует
, тогда из (39.1) следует
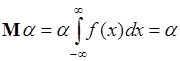 , (39.2)
, (39.2)
поскольку для плотности 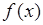 выполняется условие нормировки (33.6). Таким образом, математическое ожидание постоянной равно самой постоянной.
выполняется условие нормировки (33.6). Таким образом, математическое ожидание постоянной равно самой постоянной.
2. Пусть 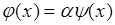 , где
, где 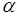 - число и
- число и 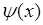 - однозначная функция одной переменной, тогда из (39.1) следует
- однозначная функция одной переменной, тогда из (39.1) следует
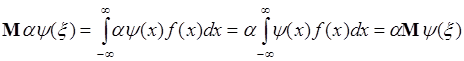 . (39.3)
. (39.3)
Таким образом, постоянный множитель 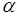 можно вынести за знак математического ожидания.
можно вынести за знак математического ожидания.
3. Пусть 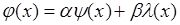 , где
, где 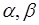 - числа,
- числа, 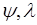 - однозначные функции одной переменной, тогда из (39.1) следует
- однозначные функции одной переменной, тогда из (39.1) следует
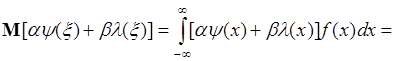
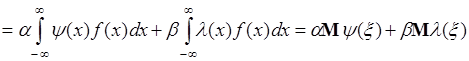 . (39.4)
. (39.4)
Из этого равенства при 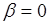 следует свойство 2, а при
следует свойство 2, а при 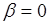 и
и 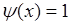 - свойство 1.
- свойство 1.
Математическое ожидание 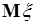 - это число, которое ставится в соответствие случайной величине
- это число, которое ставится в соответствие случайной величине  . Поэтому
. Поэтому 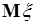 можно рассматривать как операцию (оператор, функцию) над случайной величиной
можно рассматривать как операцию (оператор, функцию) над случайной величиной  . В соответствии со свойствами 1-3 оператор математического ожидания является линейным оператором.
. В соответствии со свойствами 1-3 оператор математического ожидания является линейным оператором.
40.1.
Дисперсией случайной величины  называется число
называется число
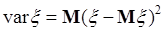 . (40.1)
. (40.1)
Дисперсия является удобной характеристикой разброса значений  около ее среднего значения
около ее среднего значения 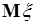 . Часто используется для обозначения дисперсии символ
. Часто используется для обозначения дисперсии символ 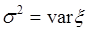 . Тогда
. Тогда 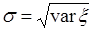 называется среднеквадратическим уклонением случайной величины
называется среднеквадратическим уклонением случайной величины  . Если дисперсия имеет размерность квадрата случайной величины, то размерность
. Если дисперсия имеет размерность квадрата случайной величины, то размерность 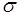 совпадает с размерностью случайной величины. Из (40.1) в соответствии со свойствами математического ожидания следует
совпадает с размерностью случайной величины. Из (40.1) в соответствии со свойствами математического ожидания следует
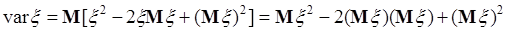 . (40.2)
. (40.2)
Таким образом,
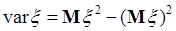 . (40.3)
. (40.3)
Если  дискретная случайная величина со значениями
дискретная случайная величина со значениями 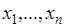 и соответствующими вероятностями
и соответствующими вероятностями 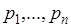 , то ее дисперсия
, то ее дисперсия
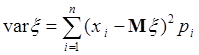 (40.4)
(40.4)
Если  - непрерывная случайная величина и
- непрерывная случайная величина и 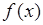 - ее плотность вероятности, то
- ее плотность вероятности, то
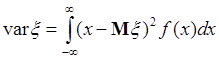 . (40.5)
. (40.5)
40.2.
Рассмотрим примеры. Вычислим дисперсию нормальной случайной величины. Ее плотность 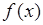 определяется формулой (35.4). Подставим
определяется формулой (35.4). Подставим 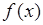 в (40.5), тогда
в (40.5), тогда
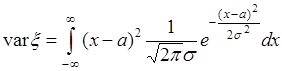 . (40.6)
. (40.6)
Пусть 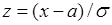 , тогда
, тогда 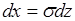 ,
,
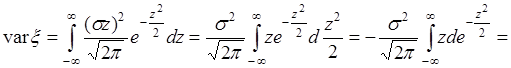
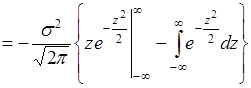 . (40.7)
. (40.7)
Подстановка пределов в (40.7) дает нулевые результаты, а интеграл равен  . Поэтому
. Поэтому
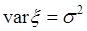 . (40.8)
. (40.8)
Таким образом, параметр 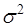 в плотности нормальной случайной величины является дисперсией этой величины, а среднеквадратичное уклонение
в плотности нормальной случайной величины является дисперсией этой величины, а среднеквадратичное уклонение 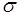 определяет эффективную ширину плотности
определяет эффективную ширину плотности 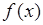 : значение
: значение 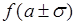 в
в 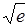 раз меньше значения
раз меньше значения 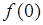 - в точке максимума.
- в точке максимума.
40.3.
В некоторых случаях для вычисления дисперсии удобно использовать формулу (40.3). Например, для экспоненциально распределенной случайной величины  плотность имеет вид (35.8), а ее среднее
плотность имеет вид (35.8), а ее среднее 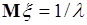 . Вычислим
. Вычислим
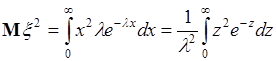 . (40.9)
. (40.9)
Интеграл в (40.9) вычисляется по частям:
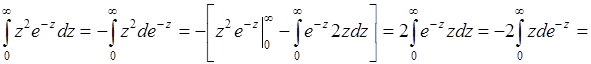
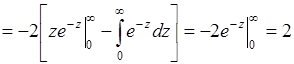 .
.
Таким образом, 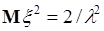 . Полученный результат подставим в формулу (40.3), тогда
. Полученный результат подставим в формулу (40.3), тогда
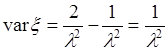 . 40.10)
. 40.10)
40.4.
Вычислим дисперсию числа успехов в вероятностной схеме Бернулли, как пример вычисления дисперсии дискретной случайной величины. При этом также используем формулу (40.3), т.е. на первом шаге вычислим среднее от квадрата 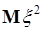 , а затем используя ранее полученный результат, дисперсию по формуле (40.3). Итак, среднее от квадрата
, а затем используя ранее полученный результат, дисперсию по формуле (40.3). Итак, среднее от квадрата
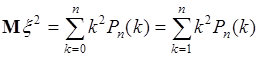 , (40.11)
, (40.11)
где 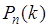 - распределение вероятностей Бернулли, поэтому
- распределение вероятностей Бернулли, поэтому
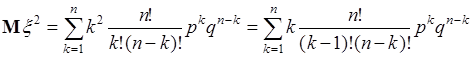 . (40.12)
. (40.12)
Пусть 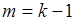 , тогда
, тогда 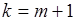 и
и
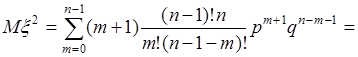
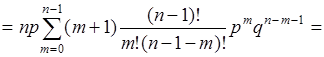 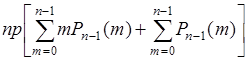 .(40.13)
.(40.13)
Здесь 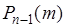 - вероятность появления
- вероятность появления 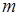 успехов в последовательности из
успехов в последовательности из 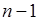 опытов. Поэтому
опытов. Поэтому 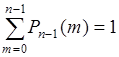 , как вероятность достоверного события, состоящего в том, что число успехов будет любым в интервале от
, как вероятность достоверного события, состоящего в том, что число успехов будет любым в интервале от 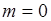 до
до 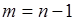 . Первая сумма в (40.13)
. Первая сумма в (40.13) 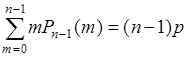 как математическое ожидание числа успехов в последовательности из
как математическое ожидание числа успехов в последовательности из 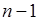 опытов в соответствии с формулой (38.9). Подставим эти результаты в (40.13), тогда
опытов в соответствии с формулой (38.9). Подставим эти результаты в (40.13), тогда
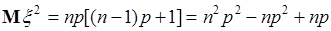 . (40.14)
. (40.14)
Теперь
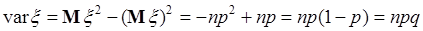 . (40.15)
. (40.15)
41.1.
Математическое ожидание и дисперсия являются примерами моментов случайной величины, которые определяются следующим образом.
Начальным моментом порядка 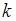 непрерывной случайной величины с плотностью распределения вероятности
непрерывной случайной величины с плотностью распределения вероятности 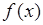 называется число
называется число
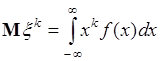 . (41.1)
. (41.1)
Порядок момента 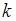 - это неотрицательное целое число, т.е.
- это неотрицательное целое число, т.е. 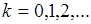 .
.
Начальным моментом порядка 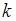 дискретной случайной величины
дискретной случайной величины  , принимающей значения
, принимающей значения 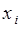 с вероятностями
с вероятностями 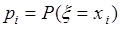 ,
, 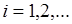 , называется число
, называется число
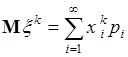 . (41.2)
. (41.2)
Определение (41.1) можно рассматривать как универсальное определение для непрерывных и для дискретных случайных величин. В последнем случае плотность вероятности выражается через 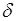 - функцию согласно формуле (34.4). Однако на практике для вычисления момента дискретной величины удобнее использовать соотношение (41.2).
- функцию согласно формуле (34.4). Однако на практике для вычисления момента дискретной величины удобнее использовать соотношение (41.2).
Центральным моментом порядка 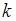 случайной величины
случайной величины  называется число
называется число
 . (41.3)
. (41.3)
Для непрерывной случайной величины  с плотностью вероятности
с плотностью вероятности 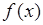 центральный момент порядка
центральный момент порядка 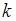 имеет вид:
имеет вид:
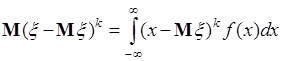 . (41.4)
. (41.4)
41.2.
Из всего множества начальных и центральных моментов обычно используются моменты невысоких порядков, до 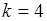 включительно, как более простые характеристики случайной величины. Применение моментов высоких порядков,
включительно, как более простые характеристики случайной величины. Применение моментов высоких порядков, 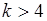 , ограничено. Во-первых, при больших
, ограничено. Во-первых, при больших 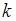 моменты могут не существовать, поскольку могут расходиться интегралы (41.1), (41.4). И во-вторых, интерпретация моментов высших порядков затруднена.
моменты могут не существовать, поскольку могут расходиться интегралы (41.1), (41.4). И во-вторых, интерпретация моментов высших порядков затруднена.
Рассмотрим начальные моменты, начиная с 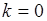 . При этом из (41.1) следует
. При этом из (41.1) следует
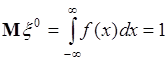 . (41.5)
. (41.5)
Итак, начальный момент нулевого порядка 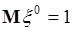 для любой случайной величины, следовательно, этот момент не отражает каких-либо свойств случайной величины, т.е. не является ее характеристикой. При
для любой случайной величины, следовательно, этот момент не отражает каких-либо свойств случайной величины, т.е. не является ее характеристикой. При 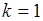 из (41.1) следует, что момент первого порядка - это математическое ожидание случайной величины. Разные случайные величины могут иметь разные математические ожидания, и поэтому число
из (41.1) следует, что момент первого порядка - это математическое ожидание случайной величины. Разные случайные величины могут иметь разные математические ожидания, и поэтому число 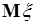 является характеристикой случайной величины: число
является характеристикой случайной величины: число 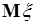 указывает положение центра ее плотности вероятности.
указывает положение центра ее плотности вероятности.
Момент второго порядка
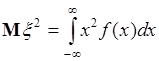 (41.6)
(41.6)
- это среднее квадрата 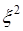 случайной величины, и т.д.
случайной величины, и т.д.
Рассмотрим аналогично центральные моменты (41.4). При 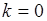 получаем
получаем 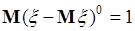 - одинаковый результат для любой случайной величины. Поэтому данный момент не является характеристикой случайной величины, поскольку не отражает каких-либо ее свойств. При
- одинаковый результат для любой случайной величины. Поэтому данный момент не является характеристикой случайной величины, поскольку не отражает каких-либо ее свойств. При 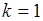
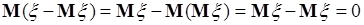 . Этот результат также одинаков для любой случайной величины, поэтому центральный момент первого порядка не является характеристикой случайной величины. При
. Этот результат также одинаков для любой случайной величины, поэтому центральный момент первого порядка не является характеристикой случайной величины. При 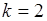 из (41.4) получаем дисперсию
из (41.4) получаем дисперсию

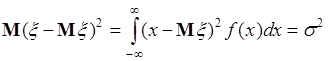 (41.7)
(41.7)
- важнейшую числовую характеристику случайной величины и т.д.
Моменты третьего и четвертого порядков будут рассмотрены в дальнейшем.
42.1. Пусть случайная величина  имеет конечный момент второго порядка
имеет конечный момент второго порядка 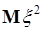 , тогда
, тогда
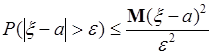 , (42.1)
, (42.1)
где 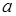 - любое действительное число и
- любое действительное число и 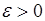 . Соотношение (42.1) называют неравенством Чебышева.
. Соотношение (42.1) называют неравенством Чебышева.
Сначала рассмотрим доказательство неравенства, следующего из (42.1) при 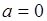 :
:
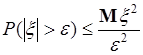 . (42.2)
. (42.2)
Доказательство неравенства Чебышева удобнее рассматривать отдельно для непрерывной и для дискретной случайных величин. При этом доказательства являются относительно простыми, а ход доказательств вполне очевиден. В то время как универсальное доказательство, справедливое и для непрерывной и для дискретной случайных величин оказывается значительно более сложным. Рассмотрим непрерывную случайную величину  с плотностью вероятности
с плотностью вероятности 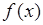 . Тогда в соотношении
. Тогда в соотношении 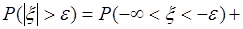
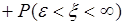 первое слагаемое можно представить в виде
первое слагаемое можно представить в виде
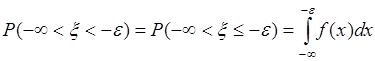 ,
,
поэтому
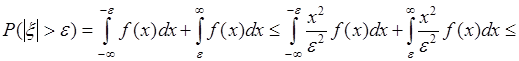 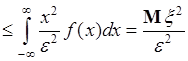 .
.
Здесь использовано неравенство 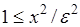 - справедливое на области интегрирования. Полученное выражение совпадает с неравенством (42.2). Аналогично выполняется доказательство для дискретной случайной величины.
- справедливое на области интегрирования. Полученное выражение совпадает с неравенством (42.2). Аналогично выполняется доказательство для дискретной случайной величины.
Теперь случайную величину  в (42.2) можно заменить на случайную величину
в (42.2) можно заменить на случайную величину 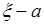 , где
, где 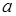 - любое действительное число, тогда из (42.2) следует неравенство Чебышева (42.1). Это неравенство определяет границу сверху для вероятности
- любое действительное число, тогда из (42.2) следует неравенство Чебышева (42.1). Это неравенство определяет границу сверху для вероятности 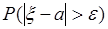 или, как говорят, больших уклонений
или, как говорят, больших уклонений 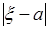 случайной величины
случайной величины  от числа
от числа 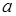 . Большие уклонения понимаются в смысле их превышения над заданным числом
. Большие уклонения понимаются в смысле их превышения над заданным числом 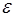 .
.
42.2. Пусть 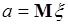 , тогда неравенство Чебышева (42.1) имеет вид
, тогда неравенство Чебышева (42.1) имеет вид
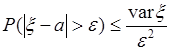 . (42.3)
. (42.3)
Теперь минимальное уклонение 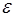 можно измерять в единицах среднеквадратического уклонения
можно измерять в единицах среднеквадратического уклонения 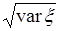 случайной величины
случайной величины  , т.е. положить
, т.е. положить
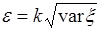 , (42.4)
, (42.4)
где 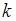 - коэффициент пропорциональности. Подставим (42.4) в (42.3), тогда
- коэффициент пропорциональности. Подставим (42.4) в (42.3), тогда
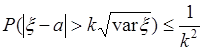 . (42.5)
. (42.5)
Если правая часть 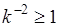 , то (42.5) не представляет какого-либо ограничения на случайную величину, поскольку вероятность
, то (42.5) не представляет какого-либо ограничения на случайную величину, поскольку вероятность 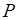 не может выходить за пределы интервала
не может выходить за пределы интервала 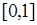 . Поэтому коэффициент
. Поэтому коэффициент 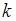 в (42.5) имеет смысл рассматривать только большим:
в (42.5) имеет смысл рассматривать только большим: 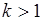 . Отсюда очевидна интерпретация неравенства Чебышева как неравенства, определяющего границу сверху вероятности больших уклонений.
. Отсюда очевидна интерпретация неравенства Чебышева как неравенства, определяющего границу сверху вероятности больших уклонений.
Пусть  - непрерывная случайная величина с плотностью вероятности
- непрерывная случайная величина с плотностью вероятности 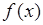 , тогда неравенству Чебышева (42.1) можно дать простую геометрическую интерпретацию, представленную на рис. 42.1.
, тогда неравенству Чебышева (42.1) можно дать простую геометрическую интерпретацию, представленную на рис. 42.1.
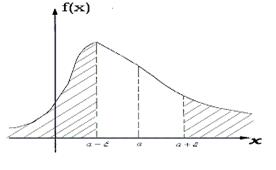
Рис. 42.1. Иллюстрация к неравенству Чебышева.
Здесь указаны числа 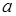 ,
, 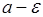 и
и 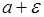 , заштрихованная площадь - это вероятность
, заштрихованная площадь - это вероятность
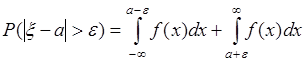 .
.
Среднее и дисперсия случайной величины 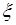 - это числа, которые определяют такие свойства ее плотности вероятности
- это числа, которые определяют такие свойства ее плотности вероятности 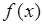 как положение центра и эффективную ширину. Очевидно, эти два числа не отражают всех особенностей плотности, в частности, степень симметрии или асимметрии плотности относительно математического ожидания - это новая характеристика, которую можно определить как некоторое число.
как положение центра и эффективную ширину. Очевидно, эти два числа не отражают всех особенностей плотности, в частности, степень симметрии или асимметрии плотности относительно математического ожидания - это новая характеристика, которую можно определить как некоторое число.
Для любой симметричной плотности 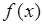 центральные моменты нечетного порядка равны нулю (доказательство приводится ниже). Поэтому простейший среди них - центральный момент третьего порядка может характеризовать асимметрию плотности распределения:
центральные моменты нечетного порядка равны нулю (доказательство приводится ниже). Поэтому простейший среди них - центральный момент третьего порядка может характеризовать асимметрию плотности распределения:
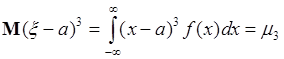 , (43.1)
, (43.1)
где 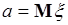 - математическое ожидание,
- математическое ожидание, 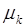 - центральный момент
- центральный момент 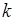 - го порядка.
- го порядка.
Асимметрию принято характеризовать коэффициентом асимметрии
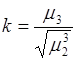 , (43.2)
, (43.2)
где 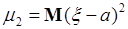 - дисперсия случайной величины
- дисперсия случайной величины 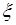 .
.
Рассмотрим доказательство утверждения о том, что для симметричной плотности 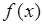 центральные моменты нечетных порядков равны нулю.
центральные моменты нечетных порядков равны нулю.
1). Пусть 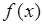 - симметричная функция относительно некоторой точки
- симметричная функция относительно некоторой точки 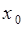 , тогда
, тогда
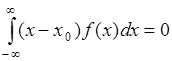 , (43.3)
, (43.3)
поскольку 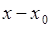 - антисимметричная функция относительно
- антисимметричная функция относительно 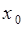 . Отсюда следует:
. Отсюда следует:
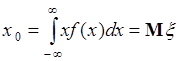 . (43.4)
. (43.4)
Таким образом, если 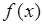 - симметричная функция относительно точки
- симметричная функция относительно точки 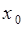 , то
, то 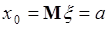 - точка симметрии плотности вероятности – это математическое ожидание случайной величины.
- точка симметрии плотности вероятности – это математическое ожидание случайной величины.
2). Пусть 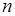 - нечетное целое и
- нечетное целое и 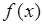 - симметричная функция, тогда
- симметричная функция, тогда 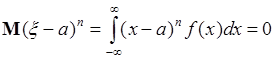 , поскольку
, поскольку 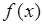 - симметрична относительно математического ожидания
- симметрична относительно математического ожидания 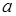 , и
, и 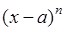 - антисимметрична относительно
- антисимметрична относительно 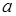 .
.
Выражение (43.2) для 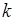 можно представить через начальные моменты
можно представить через начальные моменты 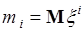 ,
, 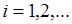 . Из определения следует:
. Из определения следует:
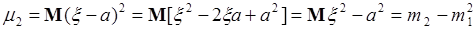 .
.
Аналогично центральный момент третьего порядка
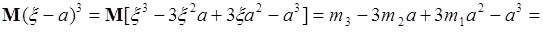
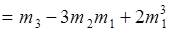 .
.
Пусть случайная величина 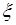 имеет плотность вероятности:
имеет плотность вероятности:
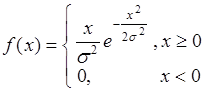 , (43.6)
, (43.6)
(распределение Рэлея), тогда вычисление 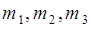 и подстановка в (43.2) приводит к результату
и подстановка в (43.2) приводит к результату 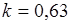 .
.
Плотность вероятности с  имеет более тяжелый «хвост» в области больших положительных аргументов, и наоборот, при
имеет более тяжелый «хвост» в области больших положительных аргументов, и наоборот, при 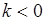 более тяжелым является «хвост» плотности в области отрицательных аргументов.
более тяжелым является «хвост» плотности в области отрицательных аргументов.
Характеристикой степени сглаженности вершины плотности вероятности является число
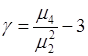 , (43.1)
, (43.1)
называемое коэффициентом эксцесса.
Определим 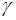 для нормального распределения. Поскольку
для нормального распределения. Поскольку 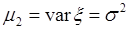 , то осталось вычислить
, то осталось вычислить
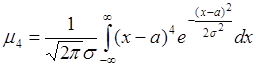 .
.
Пусть 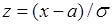 , тогда
, тогда
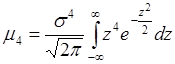 .
.
Вычислим интеграл способом «по частям»:
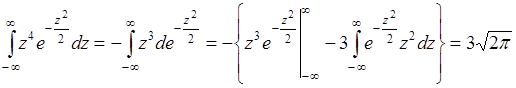 .
.
Таким образом, 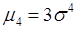 . Подставим полученные результаты в (43.6), тогда
. Подставим полученные результаты в (43.6), тогда 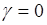 .
.
Если 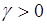 , то плотность вероятности имеет более высокую и более острую вершину, чем кривая плотности нормального распределения с той же дисперсией. Если
, то плотность вероятности имеет более высокую и более острую вершину, чем кривая плотности нормального распределения с той же дисперсией. Если 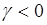 , то вершина плотности распределения более плоская, чем у нормального распределения.
, то вершина плотности распределения более плоская, чем у нормального распределения.
Пусть 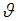 - неизвестный параметр (число), характеризующий состояние системы. Для определения параметра
- неизвестный параметр (число), характеризующий состояние системы. Для определения параметра 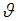 проводится опыт (измерение). Ситуация осложняется тем, что в процессе измерения на величину
проводится опыт (измерение). Ситуация осложняется тем, что в процессе измерения на величину 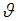 накладывается помеха. Таким образом, измерению подлежит не число
накладывается помеха. Таким образом, измерению подлежит не число 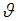 , а некоторая случайная величина
, а некоторая случайная величина 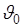 , значения которой в каждом опыте точно предсказать невозможно.
, значения которой в каждом опыте точно предсказать невозможно.
Случайную величину 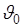 будем называть оценкой параметра
будем называть оценкой параметра 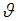 . Тогда
. Тогда 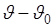 - ошибка, также случайная величина. Характеристикой качества оценки
- ошибка, также случайная величина. Характеристикой качества оценки 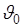 является ее среднеквадратическая ошибка
является ее среднеквадратическая ошибка
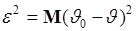 . (45.1)
. (45.1)
Преобразуем это выражение:
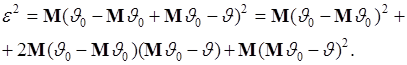 (45.2)
(45.2)
Величина 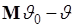 - детерминированная, поэтому ее можно вынести за оператор
- детерминированная, поэтому ее можно вынести за оператор 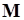 , следовательно, второе слагаемое
, следовательно, второе слагаемое
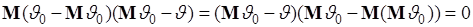
Первое слагаемое (45.2) по определению
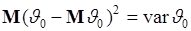
- дисперсия случайной величины 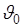 . Введем обозначение
. Введем обозначение
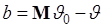 . (45.3)
. (45.3)
Число 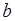 называется смещением оценки
называется смещением оценки 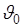 . Таким образом, из (45.2) следует
. Таким образом, из (45.2) следует
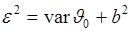 (45.4)
(45.4)
- среднеквадратическая ошибка является суммой двух неотрицательных слагаемых. Первое из них – дисперсия, или случайная (стохастическая) компонента ошибки, а второе – квадрат смещения – систематическая ошибка. Если 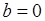 , то оценка
, то оценка 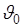 называется несмещенной.
называется несмещенной.
Пусть случайная величина 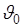 - имеет плотность вероятности
- имеет плотность вероятности 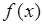 . Тогда процедуре измерения можно дать геометрическую интерпретацию. На рис. 45.1 представлен график плотности вероятности оценки и показана систематическая ошибка
. Тогда процедуре измерения можно дать геометрическую интерпретацию. На рис. 45.1 представлен график плотности вероятности оценки и показана систематическая ошибка 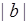 , и случайная ошибка
, и случайная ошибка 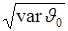 .
.
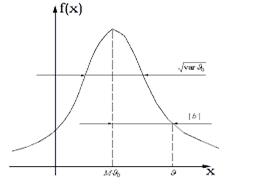
Рис. 45.1. Плотность вероятности оценки,
случайная и систематическая части ошибки.
Очевидно, идеальная процедура измерения (с нулевой среднеквадратической ошибкой) – это процедура, для которой плотность 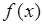 близка к функции
близка к функции 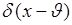 . Тогда
. Тогда 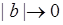 , точка
, точка 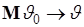 , а эффективная ширина
, а эффективная ширина 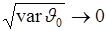 .
.
Характеристической функцией случайной величины 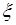 называется функция
называется функция
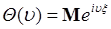 ,
, 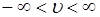 . (46.1)
. (46.1)
Пусть 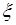 - непрерывная случайная величина с плотностью вероятности
- непрерывная случайная величина с плотностью вероятности 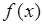 , тогда ее характеристическая функция
, тогда ее характеристическая функция
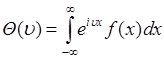 (46.2)
(46.2)
- является интегральным преобразованием, которое называется преобразованием Фурье от плотности вероятности 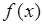 . Известно, что преобразование Фурье является взаимно однозначным. Поэтому существует обратное преобразование, которое определяет плотность вероятности
. Известно, что преобразование Фурье является взаимно однозначным. Поэтому существует обратное преобразование, которое определяет плотность вероятности 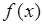 через характеристическую функцию
через характеристическую функцию 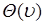 . Это преобразование имеет вид
. Это преобразование имеет вид
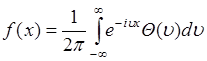 . (46.3)
. (46.3)
Соотношения (46.2) и (46.3) образуют пару преобразований Фурье.
Для дискретной случайной величины 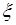 , принимающей значения
, принимающей значения 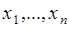 с вероятностями
с вероятностями 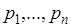 характеристическая функция, как следует из (46.1), имеет вид
характеристическая функция, как следует из (46.1), имеет вид
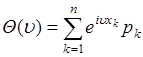 . (46.4)
. (46.4)
Характеристическая функция является полной вероятностной характеристикой случайной величины, также как и функция распределения 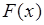 или плотность вероятности
или плотность вероятности 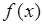 . Смысл введения характеристической функции в теории вероятности состоит в том, что имеется класс задач, которые относительно просто решаются с применением преобразования Фурье от плотности вероятности. Роль этого преобразования оказалась столь велика, что в теории появился специальный термин «характеристическая функция» для обозначения этого преобразования.
. Смысл введения характеристической функции в теории вероятности состоит в том, что имеется класс задач, которые относительно просто решаются с применением преобразования Фурье от плотности вероятности. Роль этого преобразования оказалась столь велика, что в теории появился специальный термин «характеристическая функция» для обозначения этого преобразования.
Рассмотрим свойства функции 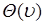 для непрерывной случайной величины. Для дискретной величины эти свойства доказываются аналогично.
для непрерывной случайной величины. Для дискретной величины эти свойства доказываются аналогично.
1). В общем случае характеристическая функция (46.2) является комплексной. Ее вещественная часть
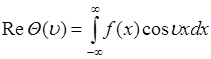 (47.1)
(47.1)
- является  - преобразованием от плотности вероятности, и мнимая часть
- преобразованием от плотности вероятности, и мнимая часть
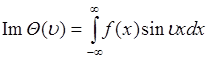 (47.2)
(47.2)
- является 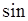 - преобразованием от
- преобразованием от 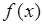 . Если
. Если 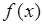 - четная функция, то
- четная функция, то 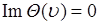 , тогда характеристическая функция
, тогда характеристическая функция 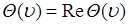 и является вещественной и четной функцией.
и является вещественной и четной функцией.
2). 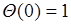 . Это свойство следует из (46.2) и условия нормировки для плотности:
. Это свойство следует из (46.2) и условия нормировки для плотности:
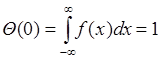 . (47.3)
. (47.3)
3). 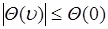 - функция
- функция 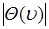 имеет глобальный максимум в точке
имеет глобальный максимум в точке 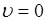 . Доказательство следует из (46.2):
. Доказательство следует из (46.2):
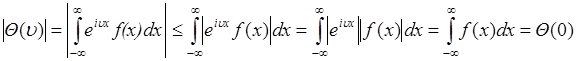 .
.
4). 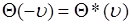
5). Характеристическая функция непрерывна. Для доказательства рассмотрим приращение 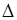 аргумента функции
аргумента функции 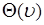 , такое, что
, такое, что 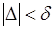 , где
, где 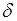 - положительное число. Тогда имеет место следующая цепочка преобразований:
- положительное число. Тогда имеет место следующая цепочка преобразований: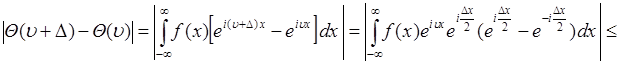
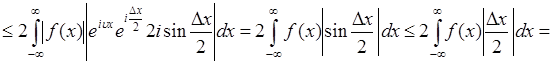
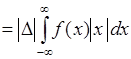 . (47.4)
. (47.4)
Пусть 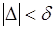 и число
и число
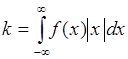 , (47.5)
, (47.5)
тогда из (47.4) следует
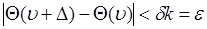 . (47.6)
. (47.6)
Таким образом, выполняется определение непрерывности функции 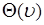 : для любого
: для любого 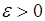 можно выбрать положительное
можно выбрать положительное 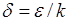 , что из условия
, что из условия 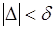 следует
следует 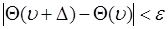 .
.
48.1. Пусть 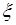 - случайная величина с характеристической функцией
- случайная величина с характеристической функцией 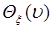 . Найти характеристическую функцию
. Найти характеристическую функцию 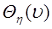 случайной величины
случайной величины
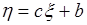 , (48.1)
, (48.1)
где 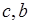 - числа. По определению
- числа. По определению
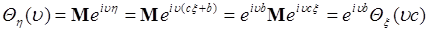 . (48.2)
. (48.2)
48.2. Найти характеристическую функцию 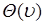 гауссовой случайной величины
гауссовой случайной величины 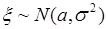 . По формуле (46.2)
. По формуле (46.2)
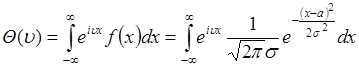 . (48.3)
. (48.3)
Выполним замену переменной интегрирования 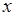 на переменную
на переменную 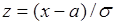 , тогда
, тогда 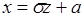 и
и
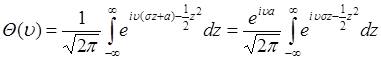 . (48.4)
. (48.4)
Показатель в подынтегральном выражении преобразуем следующим образом:
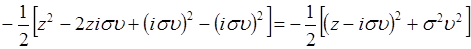 .
.
Подстановка этого результата в (48.4) приводит к выражению
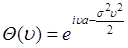 . (48.5)
. (48.5)
Отсюда следует, что характеристическая функция гауссовой случайной величины 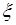 при
при 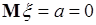 является вещественной и четной функцией.
является вещественной и четной функцией.
49.1. Вычислим производную порядка 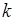 характеристической функции (46.1) при
характеристической функции (46.1) при 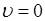 :
:
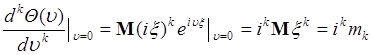 , (49.1)
, (49.1)
где 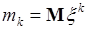 - начальный момент
- начальный момент 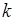 порядка случайной величины
порядка случайной величины 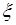 . Пусть существуют все моменты
. Пусть существуют все моменты 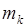 ,
, 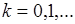 , тогда существуют производные (49.1) характеристической функции при
, тогда существуют производные (49.1) характеристической функции при 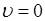 . Поэтому функцию
. Поэтому функцию 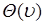 можно разложить в ряд Тейлора около точки
можно разложить в ряд Тейлора около точки 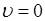 :
:
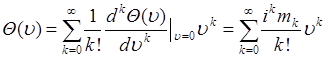 . (49.2)
. (49.2)
Отметим, что здесь первое слагаемое 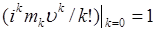 . Выражение (49.2) называют иногда разложением характеристической функции по моментам, имея ввиду тот факт, что коэффициенты при
. Выражение (49.2) называют иногда разложением характеристической функции по моментам, имея ввиду тот факт, что коэффициенты при 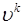 определяются начальными моментами
определяются начальными моментами 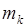 .
.
Для непрерывной случайной величины с плотностью вероятности 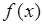 соотношение (49.1) можно представить в виде:
соотношение (49.1) можно представить в виде:
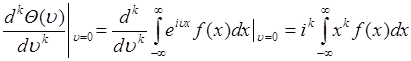 . (49.3)
. (49.3)
Таким образом, существование производной порядка 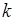 характеристической функции при
характеристической функции при 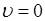 (или начального момента
(или начального момента 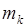 ) определяется поведением плотности вероятности
) определяется поведением плотности вероятности 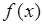 при
при 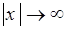 , от которого зависит существование интеграла (49.3).
, от которого зависит существование интеграла (49.3).
49.2. Функция
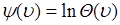 (49.4)
(49.4)
называется кумулянтной функцией случайной величины 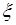 . Кумулянтная функция является полной вероятностной характеристикой случайной величины, также, как и
. Кумулянтная функция является полной вероятностной характеристикой случайной величины, также, как и 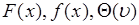 . Смысл введения кумулянтной фукнции заключается в том, что эта функция зачастую оказывается наиболее простой среди полных вероятностных характеристик, т.е. среди
. Смысл введения кумулянтной фукнции заключается в том, что эта функция зачастую оказывается наиболее простой среди полных вероятностных характеристик, т.е. среди 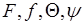 . Например, для гауссовой случайной величины из (48.5) следует
. Например, для гауссовой случайной величины из (48.5) следует
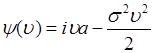 . (49.5)
. (49.5)
Кумулянтную функцию можно представить рядом, аналогично соотношению (49.2) для характеристической функции:
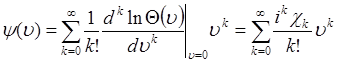 , (49.6)
, (49.6)
где число
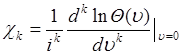 (49.7)
(49.7)
называется кумулянтом 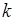 порядка случайной величины
порядка случайной величины 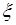 . Из (49.7) следует
. Из (49.7) следует 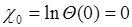 , поэтому суммирование в (49.6) можно начинать с
, поэтому суммирование в (49.6) можно начинать с 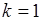 , а поскольку
, а поскольку 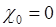 для любой случайной величины, то
для любой случайной величины, то 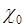 не является характеристикой случайной величины.
не является характеристикой случайной величины.
Вычислим кумулянты для гауссовой случайной величины. Из (49.7), (49.5)
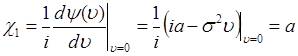 , (49.8)
, (49.8)
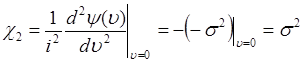 . (49.9)
. (49.9)
Для 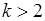 производная
производная 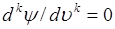 , следовательно, гауссова случайная величина имеет только два кумулянта
, следовательно, гауссова случайная величина имеет только два кумулянта 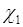 и
и 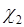 отличных от нуля, остальные кумулянты - нулевые. Поэтому ряд (49.6) для гауссовой величины состоит из двух слагаемых.
отличных от нуля, остальные кумулянты - нулевые. Поэтому ряд (49.6) для гауссовой величины состоит из двух слагаемых.
|