Самарский государственный аэрокосмический университет
им. академика С.П. Королева
Кафедра прикладной математики
Расчетно-графическая работ по курсу «Теория вероятностей и математическая статистика»
Тема работы
: «
Определение законов распределения случайных величин и их числовых характеристик на основе опытных данных. Проверка статистических гипотез»
Вариант № 15
Выполнил студент группы № 625
Евгений В. Репекто
Самара - 2002
Задание на расчетно-графическую работу
Дан протокол содержащий 120
пронумерованных значений:
| № |
№ |
№ |
№ |
| 1 |
4 |
31 |
10 |
61 |
20 |
91 |
44 |
| 2 |
19 |
32 |
25 |
62 |
16 |
92 |
12 |
| 3 |
25 |
33 |
38 |
63 |
15 |
93 |
16 |
| 4 |
-4 |
34 |
1 |
64 |
32 |
94 |
9 |
| 5 |
58 |
35 |
19 |
65 |
52 |
95 |
12 |
| 6 |
34 |
36 |
55 |
66 |
-5 |
96 |
40 |
| 7 |
32 |
37 |
9 |
67 |
21 |
97 |
17 |
| 8 |
36 |
38 |
11 |
68 |
30 |
98 |
10 |
| 9 |
37 |
39 |
6 |
69 |
27 |
99 |
31 |
| 10 |
4 |
40 |
31 |
70 |
12 |
100 |
49 |
| 11 |
24 |
41 |
17 |
71 |
19 |
101 |
25 |
| 12 |
3 |
42 |
-6 |
72 |
1 |
102 |
33 |
| 13 |
48 |
43 |
14 |
73 |
23 |
103 |
26 |
| 14 |
36 |
44 |
9 |
74 |
7 |
104 |
19 |
| 15 |
27 |
45 |
13 |
75 |
4 |
105 |
25 |
| 16 |
20 |
46 |
25 |
76 |
16 |
106 |
34 |
| 17 |
1 |
47 |
11 |
77 |
38 |
107 |
10 |
| 18 |
39 |
48 |
18 |
78 |
40 |
108 |
24 |
| 19 |
11 |
49 |
2 |
79 |
30 |
109 |
2 |
| 20 |
16 |
50 |
29 |
80 |
14 |
110 |
38 |
| 21 |
49 |
51 |
20 |
81 |
51 |
111 |
30 |
| 22 |
25 |
52 |
48 |
82 |
17 |
112 |
10 |
| 23 |
26 |
53 |
16 |
83 |
25 |
113 |
39 |
| 24 |
30 |
54 |
29 |
84 |
34 |
114 |
1 |
| 25 |
19 |
55 |
12 |
85 |
23 |
115 |
40 |
| 26 |
32 |
56 |
-3 |
86 |
20 |
116 |
7 |
| 27 |
3 |
57 |
16 |
87 |
9 |
117 |
26 |
| 28 |
40 |
58 |
41 |
88 |
29 |
118 |
36 |
| 29 |
45 |
59 |
19 |
89 |
18 |
119 |
22 |
| 30 |
35 |
60 |
0 |
90 |
46 |
120 |
28 |
Все эти протокольные значения считаются значениями выборки
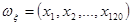
некоторой случайной величины  , а 60 из них, имеющие нечетные номера – значениями выборки , а 60 из них, имеющие нечетные номера – значениями выборки
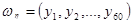
другой случайной величины 
Требуется:
1.
Построить вариационные ряды для случайных величин  и и  . .
2.
Произведя группировку элементов каждой выборки (используя формулу Стерджеса) построить статистические ряды распределения случайных величин  и и  . .
Образец заполнения таблицы для статистического ряда.
3.
Построить гистограммы распределения случайных величин  и и  . .
4.
Найти выборочное среднее 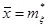 , , 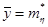 и исправленные выборочные дисперсии: и исправленные выборочные дисперсии: 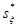 , , 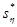 случайных величин случайных величин  и и  . .
5.
Проверить, используя метод 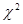 гипотезу о нормальном распределении, каждой из случайных величин гипотезу о нормальном распределении, каждой из случайных величин  и и  при уровне значимости при уровне значимости 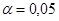 . .
6.
Построить график функции плотности распределения 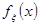 случайной величины случайной величины  в одной системе координат с гистограммой.( в одной системе координат с гистограммой.(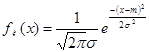 взяв в качестве математического ожидания их статистические оценки взяв в качестве математического ожидания их статистические оценки 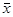 и и 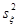 ) и вычислив значение функции ) и вычислив значение функции 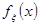 в точках: в точках: 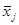 , , 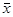 , а также в точке левее первого и правее правого промежутка группировки. , а также в точке левее первого и правее правого промежутка группировки.
7.
Выполнить задание 6 для случайной величины  . .
8.
Найти доверительные интервалы для математических ожиданий и дисперсий случайных величин  и и  , соответствующие доверительной вероятности , соответствующие доверительной вероятности 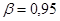 . .
9.
Проверить статистическую гипотезу 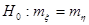 при альтернативной гипотезе при альтернативной гипотезе 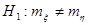 на уровне значимости на уровне значимости 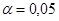 . .
10.
Проверить статистическую гипотезу 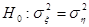 при альтернативной гипотезе при альтернативной гипотезе 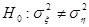 на уровне значимости на уровне значимости 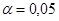 . .
Решение
1.
Построить вариационные ряды для случайных величин  и и  . .
Вариационный ряд величины 
| -6 |
12 |
22 |
33 |
| -5 |
12 |
23 |
34 |
| -4 |
12 |
23 |
34 |
| -3 |
12 |
24 |
34 |
| 0 |
13 |
24 |
35 |
| 1 |
14 |
25 |
36 |
| 1 |
14 |
25 |
36 |
| 1 |
15 |
25 |
36 |
| 1 |
16 |
25 |
37 |
| 2 |
16 |
25 |
38 |
| 2 |
16 |
25 |
38 |
| 3 |
16 |
25 |
38 |
| 3 |
16 |
26 |
39 |
| 4 |
16 |
26 |
39 |
| 4 |
17 |
26 |
40 |
| 4 |
17 |
27 |
40 |
| 6 |
17 |
27 |
40 |
| 7 |
18 |
28 |
40 |
| 7 |
18 |
29 |
41 |
| 9 |
19 |
29 |
44 |
| 9 |
19 |
29 |
45 |
| 9 |
19 |
30 |
46 |
| 9 |
19 |
30 |
48 |
| 10 |
19 |
30 |
48 |
| 10 |
19 |
30 |
49 |
| 10 |
20 |
31 |
49 |
| 10 |
20 |
31 |
51 |
| 11 |
20 |
32 |
52 |
| 11 |
20 |
32 |
55 |
| 11 |
21 |
32 |
58 |
Вариационный ряд величины 
| 1 |
21 |
| 2 |
22 |
| 2 |
23 |
| 3 |
23 |
| 4 |
24 |
| 4 |
25 |
| 6 |
25 |
| 9 |
25 |
| 9 |
25 |
| 10 |
26 |
| 10 |
26 |
| 11 |
26 |
| 11 |
27 |
| 12 |
27 |
| 12 |
30 |
| 13 |
30 |
| 14 |
31 |
| 15 |
32 |
| 16 |
37 |
| 16 |
38 |
| 16 |
38 |
| 17 |
39 |
| 17 |
40 |
| 18 |
44 |
| 19 |
45 |
| 19 |
48 |
| 19 |
49 |
| 19 |
51 |
| 20 |
52 |
| 20 |
58 |
2.
Произведя группировку элементов каждой выборки (используя формулу Стерджеса) построить статистические ряды распределения случайных величин  и и  . .
Найдем количество элементов выборок после группировки элементов
Величина  : : 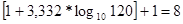
Величина  : : 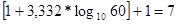
Сгруппировав элементы получим статистический ряд распределения случайной величины 
Реклама

| № пр-ка
|
Границы промежутка
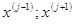
|
Середина промежутка
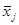
|
Количество элементов выборки в промежутке
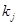
|
Частота для промежутка
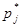
|
| 1 |
-8 ; 0 |
-4 |
4 |
0.0333 |
| 2 |
-0 ; 8 |
4 |
15 |
0.1250 |
| 3 |
8 ; 16 |
12 |
19 |
0.1583 |
| 4 |
16 ; 24 |
20 |
25 |
0.2083 |
| 5 |
24 ; 32 |
28 |
24 |
0.2000 |
| 6 |
32 ; 40 |
36 |
17 |
0.1417 |
| 7 |
40 ; 48 |
44 |
8 |
0.0667 |
| 8 |
48 ; 56 |
52 |
8 |
0.0667 |
Сгруппировав элементы получим статистический ряд распределения случайной величины 
| № пр-ка |
Границы промежутка
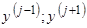
|
Середина промежутка
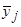
|
Количество элементов выборки в промежутке
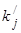
|
Частота для промежутка
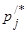
|
| 1 |
0; 9 |
4,5 |
7 |
0.1167 |
| 2 |
9 ; 18 |
13,5 |
16 |
0.2667 |
| 3 |
18 ; 27 |
22,5 |
19 |
0.3167 |
| 4 |
27 ; 36 |
31,5 |
6 |
0.1000 |
| 5 |
36 ; 45 |
40,5 |
6 |
0.1000 |
| 6 |
45 ; 54 |
49,5 |
5 |
0.0833 |
| 7 |
54 ; 63 |
58,5 |
1 |
0.0167 |
3.
Построить гистограммы распределения случайных величин  и и  . .
Гистограммы распределения приведены на графиках с теоретическими функциями распределения.
4.
Найти выборочное среднее 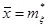 , , 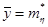 и исправленные выборочные среднеквадратические отклонения: и исправленные выборочные среднеквадратические отклонения: 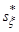 , , 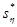 случайных величин случайных величин  и и  . .
Выборочное среднее 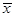 случайной величины случайной величины  равно равно
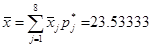
Выборочное среднее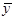 случайно величины случайно величины  равно равно
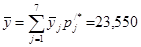
Найдем исправленное среднеквадратическое отклонение 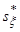 случайной величины случайной величины  : :
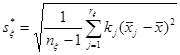 =14.3632 =14.3632
Найдем исправленное среднеквадратическое отклонение 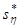 случайной величины случайной величины  : :
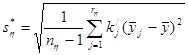 =13.5727 =13.5727
5.
Проверить, используя метод 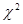 гипотезу о нормальном распределении, каждой из случайных величин гипотезу о нормальном распределении, каждой из случайных величин  и и  при уровне значимости при уровне значимости 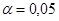 . .
Проверим гипотезу о нормальном распределении случайной величины  . .
Используя предполагаемый закон распределения, вычислим теоретические частоты по формуле
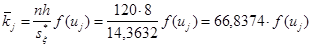 , где , где 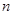 - объем выборки, - объем выборки, 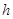 - шаг (разность между двумя соседними вариантами, - шаг (разность между двумя соседними вариантами, 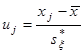 , , 
Построим вспомогательную таблицу:
 |
 |
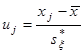 |
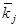 |
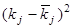 |
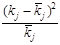 |
| 1 |
4 |
-1.9169 |
4.2461 |
0.0606 |
0.014 |
| 2 |
15 |
-1.3600 |
10.5760 |
19.572 |
1.850 |
| 3 |
19 |
-0.8030 |
19.3161 |
0.0999 |
0.005 |
| 4 |
25 |
-0.2460 |
25.8695 |
0.7561 |
0.0292 |
| 5 |
24 |
0.3110 |
25.4056 |
1.9757 |
0.0778 |
| 6 |
17 |
0.8680 |
18.2954 |
1.6780 |
0.0917 |
| 7 |
8 |
1.4249 |
9.6610 |
2.7590 |
0.2856 |
| 8 |
8 |
1.9819 |
3.7409 |
18.139 |
4.8491 |
В итоге получим 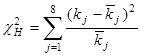 = 7,2035 = 7,2035
По таблице критических точек распределения 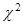 ([1], стр. 465), по уровню значимости ([1], стр. 465), по уровню значимости 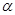 =0,05 и числу степеней свободы 8-3=5 находим =0,05 и числу степеней свободы 8-3=5 находим
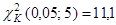
Т.к. 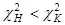 , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины  . .
Для случайной величины  : :
Используя предполагаемый закон распределения, вычислим теоретические частоты по формуле
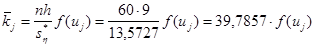 , где , где 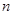 - объем выборки, - объем выборки, 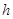 - шаг (разность между двумя соседними вариантами, - шаг (разность между двумя соседними вариантами, 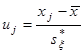 , , 
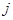 |
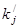 |
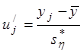 |
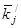 |
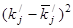 |
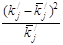 |
| 1 |
7 |
-1.4036 |
5.9274 |
1.1504 |
0.1941 |
| 2 |
16 |
-0.7405 |
12.0665 |
15.4725 |
1.2823 |
| 3 |
19 |
-0.0774 |
15.8248 |
10.0820 |
0.6371 |
| 4 |
6 |
0.5857 |
13.3702 |
54.3197 |
4.0627 |
| 5 |
6 |
1.2488 |
7.2775 |
1.6319 |
0.2242 |
| 6 |
5 |
1.9119 |
2.5519 |
5.9932 |
2.3485 |
| 7 |
1 |
2.5750 |
0.5765 |
0.1794 |
0.3111 |
В итоге получим 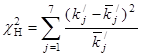 =8.1783 =8.1783
По таблице критических точек распределения 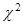 ([1], стр. 465), по уровню значимости ([1], стр. 465), по уровню значимости 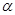 =0,05 и числу степеней свободы 7 - 3=4 находим =0,05 и числу степеней свободы 7 - 3=4 находим
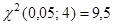
Т.к. 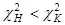 , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины  . .
6.
Построить график функции плотности распределения 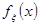 случайной величины случайной величины  в одной системе координат с гистограммой.( в одной системе координат с гистограммой.(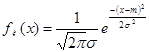 взяв в качестве математического ожидания
и дисперсии их статистические оценки взяв в качестве математического ожидания
и дисперсии их статистические оценки 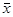 и и 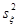 ) и вычислив значение функции ) и вычислив значение функции 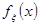 в точках: в точках: 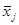 , , 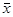 , а также в точке левее первого и правее правого промежутка группировки. , а также в точке левее первого и правее правого промежутка группировки.
7.
Выполнить задание 6 для случайной величины  . .
8.
Найти доверительные интервалы для математических ожиданий и дисперсий случайных величин  и и  , соответствующие доверительной вероятности , соответствующие доверительной вероятности 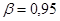 . .
Реклама

Найдем доверительный интервал для математического ожидания 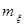 : :
Рассмотрим статистику 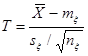 , имеющую распределение Стъюдента с , имеющую распределение Стъюдента с 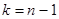 степенями свободы. Тогда требуемый доверительный интервал определится неравенством степенями свободы. Тогда требуемый доверительный интервал определится неравенством 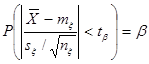 . И доверительный интервал для . И доверительный интервал для 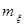 выглядит следующим образом: выглядит следующим образом:
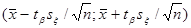
Найдем 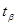 по таблицам ([2], стр. 391). По по таблицам ([2], стр. 391). По 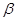 =0,95 и =0,95 и 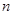 =120 находим: =120 находим: 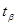 =1,980. Тогда требуемый доверительный интервал примет вид: =1,980. Тогда требуемый доверительный интервал примет вид:
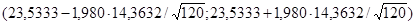
То есть: (20,93721;26,12946).
Найдем доверительный интервал для математического ожидания 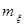 : :
Рассмотрим статистику 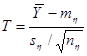 , имеющую распределение Стъюдента с , имеющую распределение Стъюдента с 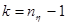 степенями свободы. Тогда требуемый доверительный интервал определится неравенством степенями свободы. Тогда требуемый доверительный интервал определится неравенством 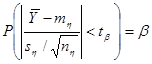 . И доверительный интервал для . И доверительный интервал для 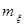 выглядит следующим образом: выглядит следующим образом:
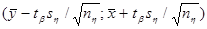
Найдем 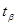 по таблицам ([2], стр. 391). По по таблицам ([2], стр. 391). По 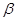 =0,95 и =0,95 и 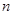 =60 находим: =60 находим: 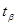 =2,001. Тогда требуемый доверительный интервал примет вид: =2,001. Тогда требуемый доверительный интервал примет вид:
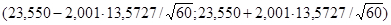
То есть: (20,043;27,056).
Известно, что если математическое ожидание неизвестно, то доверительный интервал для дисперсии при доверительной вероятности 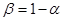 имеет вид имеет вид
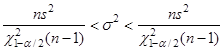
Для случайной величины  найдем: найдем:
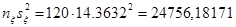 . .
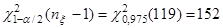
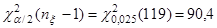
Таким образом, имеем доверительный интервал:  (162,8696; 273,8515). (162,8696; 273,8515).
Для случайной величины  найдем найдем
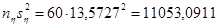
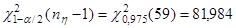
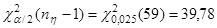
Таким образом, имеем доверительный интервал: 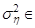 (134,82; 277,8554). (134,82; 277,8554).
(Квантили распределения 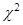 найдены по таблице [3], стр. 413). найдены по таблице [3], стр. 413).
9.
Проверить статистическую гипотезу 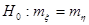 при альтернативной гипотезе при альтернативной гипотезе 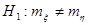 на уровне значимости на уровне значимости
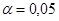 . .
Рассмотрим статистику
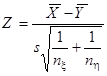 , ,
где
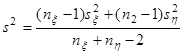 , ,
которая имеет распределение Стъюдента 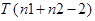 , ,
Тогда область принятия гипотезы 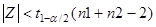 . .
Найдем s:
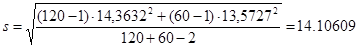
Найдем значение статистики 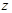 : :
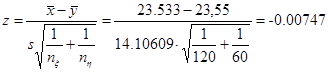
По таблице квантилей распределения Стъюдента ([2], стр. 391)
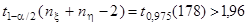
Т. к. 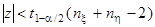 , то гипотеза , то гипотеза 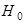 принимается. Предположение о равенстве математических ожиданий принимается. Предположение о равенстве математических ожиданий 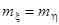 не противоречит результатам наблюдений.
не противоречит результатам наблюдений.
10.
Проверить статистическую гипотезу 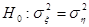 при альтернативной гипотезе при альтернативной гипотезе 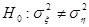 на уровне значимости на уровне значимости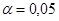 . .
Рассмотрим статистику 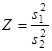 , где , где 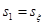 , , 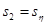 т.к. т.к. 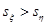 . Эта статистика имеет распределение Фишера . Эта статистика имеет распределение Фишера 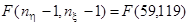 . Область принятия гипотезы . Область принятия гипотезы 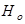
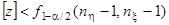
Найдем значение статистики 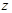 : :
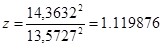
По таблицам найдем 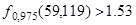 . Т.к. . Т.к. 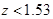 , то гипотеза , то гипотеза 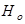 принимается. Предположение принимается. Предположение 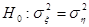 не противоречит результатам наблюдений.
не противоречит результатам наблюдений.
Библиографический список
1. Сборник задач по математике для втузов. Ч. 3. Теория вероятностей и математическая статистика: Учеб. пособие для втузов / Под. ред. А.В. Ефимова. – 2-е изд., перераб. и доп. – М.: Наука. Гл. ред. физ.-мат. лит. , 1990. – 428 с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 4-е, стер. М.: Высш. Шк., 1997. – 400 с.: ил.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для втузов. Изд. 5-е, перераб. и доп. М., «Высш. школа», 1977.
4. Вентцель Е.С. Теория вероятностей. – М.: 1969, 576 с.
|