Министерство образования и науки РФ
ГОУ ВПО
Саратовский государственный технический университет
Кафедра «Электронные приборы и устройства»
Курсовая работа на тему:
«Оценка погрешностей измерений»
Саратов 2010
Задание к курсовой работе
Заданная выборка имеет вид:
| 72,9137 |
72,2243 |
73,2806 |
732304 |
75,6094 |
| 73,3917 |
72,5557 |
74,4357 |
72,448 |
72,325 |
| 70,5713 |
72,6716 |
71,0304 |
70,5799 |
71,767 |
| 71,6886 |
73,5431 |
72,9935 |
73,2538 |
72,9033 |
| 74,2542 |
72,959 |
73,0988 |
72,738 |
73,08 |
| 70,3713З |
74.9595 |
71,5632 |
73,943 |
74,5532 |
| 73.5407 |
71,1872 |
71,4221 |
71,2018 |
74,2139 |
| 73,8979 |
75,7989 |
71,4815 |
72,0882 |
70,1388 |
| 73,9814 |
73,1069 |
74,173 |
74,5629 |
73,654 |
| 73,0471 |
72,372 |
72,5726 |
70,7069 |
73,1002 |
| 73,9612 |
73.7216 |
73,1189 |
72,1772 |
71,1006 |
| 70,5482 |
73,8402 |
74,6359 |
72,7028 |
73,4373 |
| 74,3261 |
73,5181 |
72,0133 |
71,2549 |
75,4085 |
| 73,4603 |
72,1824 |
71,8583 |
72,2526 |
73,2037 |
| 72,6318 |
72,7662 |
72,685 |
73,8493 |
74,747 |
| 71,4287 |
70,565 |
74,7288 |
75,21 |
71,6711 |
| 72.9558 |
73,223 |
74,1516 |
74,1286 |
72,7163 |
| 72,1847 |
73,0784 |
72,5307 |
74,216 |
71,9055 |
| 72,2845 |
71,7841 |
72,27 |
71,1639 |
74,0282 |
| 73,3143 |
74,2181 |
73,4217 |
70,8937 |
74,6933 |
Необходимо исследовать методы определения погрешностей и методы статистической оценки распределений. Провести расчеты по заданной выборке. При анализе выборки необходимо рассмотреть следующие параметры:
·объем выборки;
·интервальный статистический ряд и частности для каждого интервала;
·медиану распределения;
·размах вариации;
·выборочное среднее;
·выборочную дисперсию;
·среднеквадратическое отклонение;
·эмпирическую функцию распределения.
Так же рекомендуется выдвинуть гипотезу о виде распределения и провести проверку данной гипотезы.
Введение
При практическом использовании тех или иных измерений важно оценить их точность. Термин "точность измерений", т. е. степень приближения результатов измерения к некоторому действительному значению, не имеет строгого определения и используется для качественного сравнения измерительных операций. Для количественной оценки используется понятие "погрешность измерений" (чем меньше погрешность, тем выше точность). Понятие "погрешность" — одно из центральных в метрологии, где используются понятия "погрешность результата измерения" и "погрешность средства измерения". Погрешность результата измерения — это разница между результатом измерения Xи истинным (или действительным) значением Qизмеряемой величины. Она указывает границы неопределенности значения измеряемой величины. Погрешность средства измерения — разность между показанием средства измерения и истинным (действительным) значением измеряемой физической величины. Она характеризует точность результатов измерений, проводимых данным средством.
Оценка погрешности измерений — одно из важных мероприятий по обеспечению единства измерений. Количество факторов, влияющих на точность измерения, достаточно велико, и любая классификация погрешностей измерения в известной мере условна, так как различные погрешности в зависимости от условий измерительного процесса проявляются в различных группах. По характеру проявления погрешности делятся на случайные, систематические, прогрессирующие и грубые (промахи).
Реклама

Оценивание погрешностей производится с целью получения объективных данных о точности результата измерения. Погрешность измерения описывается определенной математической моделью, выбор которой обуславливается имеющимися априорными сведениями об источниках погрешности, а также данными, полученными в ходе измерений. С помощью выбранной модели определяются характеристики и параметры погрешности, используемые для количественного выражения тех или иных ее свойств.
В основу выбора оценок погрешностей положен ряд принципов. Во-первых, оцениваются отдельные характеристики и параметры выбранной модели погрешности. Это связано с тем, что модели погрешностей, как правило, сложны и описываются многими параметрами. Определение их всех весьма затруднительно, а иногда и невозможно. Кроме этого, в большинстве практических случаев полное описание модели погрешности содержит избыточную информацию, в то время как знание отдельных ее характеристик вполне достаточно для достижения цели измерения. Во-вторых, оценки погрешности определяют приближенно, с точностью, согласованной с целью измерения. Это обусловлено тем, что погрешности определяют лишь зону неопределенности результата измерения и их не требуется знать очень точно. В-третьих, погрешности оцениваются сверху, поэтому погрешность лучше преувеличить, чем преуменьшить, так как в первом случае снижается качество измерений, а во втором — возможно полное обесценивание результатов всего измерения. В-четвертых, поскольку стремятся получить реалистические значения оценки погрешности результата измерения, т.е. не слишком завышенные и не слишком заниженные, точность измерений должна соответствовать цели измерения. Излишняя точность ведет к неоправданному расходу средств и времени. Недостаточная точность в зависимости от цели измерения может привести к признанию годным в действительности негодного изделия, к принятию ошибочного решения и т. п.
Элементы теории
В основе любых измерений лежат прямые измерения, в ходе которых находят некоторое числовое значение физической величины. Каждая такая измерительная операция называется наблюдением, а получаемое при этом значение физической величины – результатом наблюдения. Получаемый опытным путем результат наблюдения подвержен случайным отклонениям от истинного значения физической величины. Такой заранее непредсказуемый в каждом данном наблюдении результат является случайной величиной. Многократное повторное проведение опыта позволяет установить статистические закономерности, которым удовлетворяет данная случайная величина.
Реклама

При каждом наблюдении мы получаем некоторое возможное значение физической величины. Всё множество возможных значений измеряемой величины, которые она может принимать в эксперименте, называется генеральной совокупностью.
Это множество может быть как конечным, так и бесконечным. Большинство физических величин имеет непрерывный набор возможных значений, множество которых является бесконечным. Говорят, что такие величины имеют генеральную совокупность бесконечного объёма.
Генеральная совокупность несет полную информацию об измеряемой величине и позволяет (в отсутствие невыявленных систематических погрешностей), несмотря на случайный характер результатов отдельных наблюдений, найти истинное значение x
0
физической величины. В случае физической величины с непрерывным набором значений для нахождения её истинного значения необходимо провести бесконечное число наблюдений, что невозможно. Поэтому на практике ограничиваются конечным числом наблюдений (от единиц до нескольких десятков). Полученный при этом ряд значений физической величины: x
1
, x
2
, ... xN
называют выборкой из генеральной
совокупности
или просто выборкой.
Ввиду ограниченного числа наблюдений в выборке, по ней нельзя найти ни истинного значения измеряемой величины, ни истинной погрешности измерения, и задача сводится к нахождению по выборке наилучших выборочных оценок (наилучших приближенных значений) истинного значения и истинной погрешности измерения.
Чтобы получить представление о законе распределения измеряемой величины, производят группировку данных. Для этого весь интервал значений величины от x
min
до x
max
(рис. 2.1) разбивают на несколько равных интервалов, называемых интервалами группировки данных, шириной Д и центрами xk
, так что k
-й интервал (k
=1, 2…K
) имеет границы (xk
– Д /2, xk
+ Д /2). Далее, распределяют значения x
1
по интервалам. Число точек Nk
, оказавшихся внутри k
-го интервала, даёт число попаданий измеряемой величины в этот интервал. Общее число точек, оказавшихся внутри всех интервалов разбиения, должно быть равно полному числу N
результатов наблюдений в исходной выборке.
Над каждым интервалом Дk
строится прямоугольник высотой
f
k
= Nk
/(N
Д),
где N
– общее число наблюдений. Совокупность таких прямоугольников называется гистограммой.
При построении гистограмм интервалы разбиения не следует брать очень большими или очень маленькими. Так, в первом случае прямоугольники на гистограмме будут иметь примерно одинаковую высоту, а во втором – могут появиться интервалы, в которые не попадет ни одного значения случайной величины. В последнем случае внутри гистограммы будут просветы. Такие гистограммы не дают представления о законе распределения случайной величины.
Высоты и площади прямоугольников на гистограмме имеют следующий смысл. Учитывая, что относительные частоты
Pk
= Nk
/N
приближенно равны вероятности попадания результата каждого отдельного наблюдения в данный интервал, высота каждого прямоугольника на гистограмме
f
k
= Nk
/N
Д= Р
k
/Д
есть вероятность, приходящаяся на единицу длины интервала разбиения или плотность вероятности попадания случайной величины в интервал Дk
с центром в точке xk
.
Площадь каждого прямоугольника
fk
Д= Nk
/N
= Р
k
есть вероятность попадания результата в интервал Дk
.. Сумма площадей прямоугольников, основания которых находятся внутри некоторого интервала [x
1
,x
2
], равна вероятности для каждого отдельного наугад взятого результата попасть в этот интервал.
Расчетная часть
В математической статистике исходная исследуемая случайная величина называется генеральной совокупностью, а полученный из нее набор экспериментальных данных – выборочной совокупностью, или выборкой.
1. Число объектов (наблюдений) в совокупности, генеральной или выборочной, называется ее объемом
; обозначается соответственно через Nи n. В данном случае N=100.
2. Числа ni
, показывающие сколько раз встречаются варианты xi
в ряде наблюдений, называются частотами
, а отношение их к объему выборки – частостями
pi
.
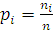 , (1) , (1)
где 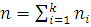 . .
Проранжируем статистические данные. Для определения оптимального значения величины интервала в первом приближении можно воспользоваться формулой Стерджеса
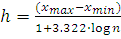 (2) (2)
Воспользовавшись (2) получим 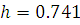 , , 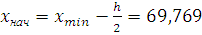 . .
В соответствии с (1) и (2) составим интервальный статический ряд:
Таблица 1
Итервальный статический ряд
| Интервал |
69,768-70,509 |
70,509-71,25 |
71,25-71,991 |
71,991-72,732 |
72,732-73,473 |
73,473-74,214 |
74,214-74,955 |
74,955-75,696 |
75,696-76,437 |
| Частота |
2 |
11 |
11 |
20 |
24 |
16 |
11 |
4 |
1 |
| Частостьpi |
0,02 |
0,11 |
0,11 |
0,2 |
0,24 |
0,16 |
0,11 |
0,04 |
0,01 |
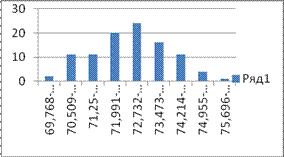
Рисунок 1. Диаграмма частоты в выбранных интервалах
3. Медианой
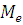 вариационного ряда называется значение признака, приходящееся на середину ряда. В нашем случае имеем: вариационного ряда называется значение признака, приходящееся на середину ряда. В нашем случае имеем:
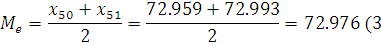
4. Размахом вариации
называется число
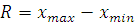 , ,
где или 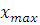 – наибольший, – наибольший, 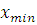 – наименьший вариант ряда. – наименьший вариант ряда.
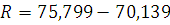
5. Выборочным средним
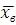 называется среднее арифметическое всех значений выборки: называется среднее арифметическое всех значений выборки:
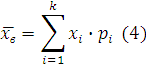
В случае интервального статистического ряда в качестве  следует брать середины интервалов, а следует брать середины интервалов, а 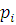 - соответствующие им частости. - соответствующие им частости.
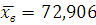
6. Выборочной дисперсией
D
в
называется среднее арифметическое квадратов отклонений значений выборки от выборочной средней, т.е.
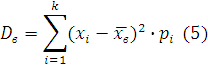
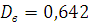
7. Выборочное среднеквадратическое отклонение
выборки определяется формулой:
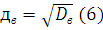
8. Эмпирической (статистической) функцией распределения
называется функция 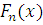 , определяющая для каждого значения x
частость события , определяющая для каждого значения x
частость события 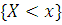 : : 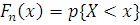 . Для нахождения эмпирической функции . Для нахождения эмпирической функции 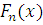 записывают в виде: записывают в виде:
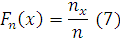
где n– объем выборке, nx
– число наблюдений, меньших х
. Согласно (7) определим значения эмпирической функции распределения в выбранных интервалах.
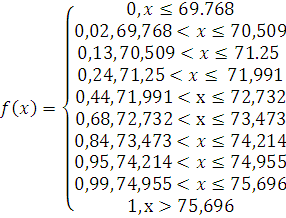
График эмпирической функции распределения имеет вид.
Одной из важных задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по эмпирическому распределению, представляющему вариационный ряд.
Проверим при уровне значимости 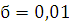 гипотезу гипотезу 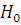 о том, что исследуемая выборка подчиняется нормальному закону распределения. о том, что исследуемая выборка подчиняется нормальному закону распределения.
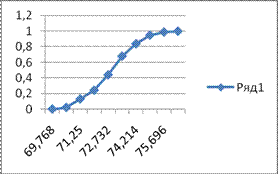
Рисунок 2. График эмпирической функции распределения
Число наблюдений в крайних интервалах меньше 5, поэтому объединим их с соседними. Получим следующий ряд распределения ( n=100).
| Интервалы |
Частота k |
Середина интервалаXcp |
| 69,768-71,25 |
13 |
70,694 |
| 71,25-71,991 |
11 |
71,62 |
| 71,991-72,732 |
20 |
72,362 |
| 72,732-73,473 |
24 |
73,102 |
| 73,473-74,214 |
16 |
73,844 |
| 74,214-74,955 |
11 |
74,584 |
| 74,955-76,437 |
5 |
75,377 |
Вычислим параметры, определяющие нормальный закон распределения.
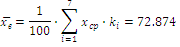
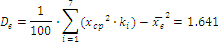
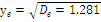
Так как случайная величина имеет нормальное распределение, то для расчета вероятностей 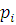 попадания случайной величины Xв интервал используем функцию Лапласа в соответствии со свойствами нормального распределения: попадания случайной величины Xв интервал используем функцию Лапласа в соответствии со свойствами нормального распределения:
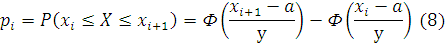
Полученные результаты приведем в следующей таблице:
| Xi
, Xi+1
|
69,768-71,25 |
71,25-71,991 |
71,991-72,732 |
72,732-73,473 |
73,473-74,214 |
74,214-74,955 |
74,955-76,437 |
| ni
|
13 |
11 |
20 |
24 |
16 |
11 |
5 |
| n`=n∙pi
|
10,2 |
14,5 |
20,92 |
22,46 |
17,69 |
9,03 |
5,2 |
Определим критерий Пирсона:
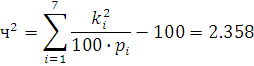
Находим число степеней свободы. По выборке рассчитаны два параметра, значит 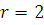 . Количество интервалов . Количество интервалов 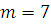 . Следовательно, . Следовательно, 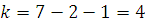 . Зная, что . Зная, что 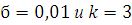 , по таблице находим , по таблице находим 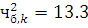 . Поскольку . Поскольку 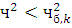 считаем гипотезу верной. считаем гипотезу верной.
9. Осуществим разбиение выборки на произвольное число интервалов, тем самым визуализировав вид плотности распределения случайной величины.
Таблица 2
Разбиение выборки на 20 и 30 интервалов
| № интервала |
Интервал |
Частота, ki |
Интервал |
Частота, ki |
| 1 |
70,138-70,327 |
1 |
70,138-70,422 |
2 |
| 2 |
70,327-70,516 |
1 |
70,422-70,705 |
4 |
| 3 |
70,516-70,705 |
4 |
70,705-70,988 |
2 |
| 4 |
70,705-70,893 |
1 |
70,988-71,271 |
6 |
| 5 |
70,836-71,082 |
2 |
71,271-71,554 |
3 |
| 6 |
71,082-71,271 |
5 |
71,554-71,837 |
5 |
| 7 |
71,271-71,459 |
2 |
71,837-72,120 |
4 |
| 8 |
71,,459-71,648 |
2 |
72,120-72,403 |
9 |
| 9 |
71,648-71,837 |
4 |
72,403-72,686 |
6 |
| 10 |
71,837-72,026 |
3 |
72,686-72,969 |
9 |
| 11 |
72,026-72,214 |
4 |
72,969-73,252 |
11 |
| 12 |
72,214-72,403 |
6 |
73,252-73,535 |
8 |
| 13 |
72,403-72,592 |
4 |
73,535-73,818 |
4 |
| 14 |
72,592-72,781 |
7 |
73,818-74,101 |
7 |
| 15 |
72,781-72,969 |
4 |
74,101-74,384 |
8 |
| 16 |
72,969-73,158 |
8 |
74,384-74,667 |
4 |
| 17 |
73,158-73,347 |
6 |
74,667-74,950 |
3 |
| 18 |
73,347-73,536 |
5 |
74,950-75,233 |
2 |
| 19 |
73,536-73,725 |
4 |
75,233-75,517 |
1 |
| 20 |
73,725-73,913 |
3 |
75,517-75,8 |
2 |
| 21 |
73,913-74,102 |
4 |
| 22 |
74,102-74,291 |
7 |
| 23 |
74,291-74,480 |
2 |
| 24 |
74,480-74,668 |
3 |
| 25 |
74,668-74,857 |
3 |
| 26 |
74,857-75,04 |
1 |
| 27 |
75,04-75,23 |
1 |
| 28 |
75,23-75,423 |
1 |
| 29 |
75,423-75,612 |
1 |
| 30 |
75,612-75,801 |
1 |
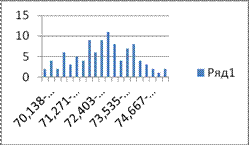
Рисунок 3. Диаграмма плотности распределения случайной величины с 20-и интервальным разбиением
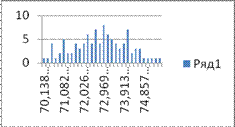
Рисунок 4. Диаграмма плотности распределения случайной величины с 30-и интервальным разбиением
Рассчитаем основные параметры выборки для 20 интервалов:
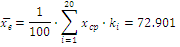
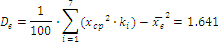

Рассчитаем основные параметры выборки для 30 интервалов:
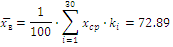
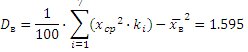
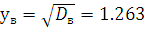
Вывод:
В ходе работы были изучены методы статистической оценки распределения случайной величины. Осуществлены расчеты по представленной выборке, рассмотрены числовые характеристики случайной величины: объем выборки, медиана распределения, размах вариации, выборочное среднее, выборочная дисперсия и среднеквадратическое отклонение.
Построена эмпирическая функция распределения, определяющая частность события для каждого значения случайной величины x
.
Установлен теоретический закон распределения с.в. Рассматриваемая случайная величина имеет нормальное распределение, что подтверждает критерий Пирсона.
Выборка также разбита на 20 и 30 интервалов. Соответствующие гистограммы дают визуальное представление о виде плотности распределения с.в. Основные числовые параметры выборки при увеличении числа интервалов практически не меняются.
Библиографический список
1) Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистики / Письменный Д.Т. - М.: Айрис пресс, 2004. - 252с.
2) Колде Я.К. Практикум по теории вероятностей и математической статистике / Колде Я.К. - М.: Высш. школа, 1991. a - 157с.
3) Сергеев А.Г., Крохин В.В. Метрология: Учеб. пособие для вузов / Сергеев А.Г., Крохин В.В. - М.: Логос, 2001. - 408 с.: ил.
4) Аристов А.И. Метрология, стандартизация, сертификация / Аристов А.И. - М.: Академия, 2008. - 384с.
5) Радкевич Я.М. Метрология, стандартизация, сертификация / Радкевич Я.М. - М.: Высшая школа, 2010 - 792 с.
6) Димов Ю.В. Метрология, стандартизация и сертификация / Димов Ю.В. - СпБ.: Питер, 2010- 464с
|