| Министерство образования и науки РФ
Федеральное государственное образовательное учреждение
высшего профессионального образования
«Чувашский государственный университет им. И. Н. Ульянова»
Факультет управления и экономики
Кафедра высшей математики и информационных технологий
Курсовая работа
По дисциплине: «Математическая логика»
На тему: «Типовые логические устройства в ЭВМ»
Выполнил студент 1-ого курса,
группы АФТ 05-10,
Петухов Дмитрий Николаевич,
Научный руководитель
асс. Мигунова Е.С.
Алатырь 2010
Содержание
Введение. - 3 -
1. Триггеры.. - 4 -
1.1. Типы триггеров. - 10 -
1.1.1.
RS-триггеры
.. - 10 -
JK-триггеры
.. - 11 -
2. Полусумматоры.. - 13 -
3. Сумматоры.. - 14 -
4. Счётчики. - 18 -
5. Регистры.. - 20 -
6.Шифратор. - 22 -
7. Дешифратор. - 23 -
Заключение. - 25 -
Список используемой литературы.. - 27 -
Введение
Данная работа посвящена рассмотрению роли типовых логических устройств в ЭВМ.
Электронная вычислительная машина (ЭВМ), компьютер – комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач.
Во всех современных компьютерах применяется логическая система, изобретения Джорджем Булем.
С развитием электроники появился такой класс электронной техники, как цифровая. Цифровая техника включает в себя такие устройства как триггеры, регистры, счётчики, комбинационные устройства, программируемые логические интегральные схемы и др.
Средством обработки двоичных сигналов в ЭВМ являются логические элементы.
Логический элемент компьютера — это часть электронной логической схемы с одним или несколькими входами и одним выходом, черех которую проходят электрические сигналы, представляющие 0, 1.
К таким устройствам относятся такие типовые логические устройства как триггер, сумматор, полусумматор, шифратор, дешифратор и счётчик. Они предназначены для формирования, обработки и передачи электрических импульсных сигналов и перепадов напряжения и тока, а также для управления информацией и её хранения одном бите, то есть 0 или 1.
Целью данной работы является рассмотрение логических устройств применяемых в ЭВМ, как они устроены и функционируют.
Объектом исследования данной работы стали логические устройства, в состав которых входят: триггеры, сумматоры, полусумматоры, регистры, счётчики, шифраторы и дешифраторы.
Реклама

Курсовое исследование написано при использовании специализированных исследований некоторых авторов. Библиографический список представлен в конце курсовой работы.
1. Триггеры
Триггер — это запоминающий элемент с двумя (или более) устойчивыми состояниями, изменение которых происходит под действием входных сигналов и предназначен для хранения одного бита информации, то есть 0 или 1.
Триггеры подразделяются на две большие группы — динамические и статические. Названы они так по способу представления выходной информации.
Динамический триггер представляет собой систему, одно из состояний которой (единичное) характеризуется наличием на выходе непрерывной последовательности импульсов определённой частоты, а другое — отсутствием выходных импульсов (нулевое). Смена состояний производится внешними импульсами (рис. 1). Динамические триггеры в настоящее время используются редко.
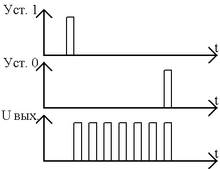
Рис. 1.
Временная диаграмма работы динамического триггера
К статическим триггерам относят устройства, каждое состояние которых характеризуется неизменными уровнями выходного напряжения (выходными потенциалами): высоким — близким к напряжению питания и низким — около нуля. Статические триггеры по способу представления выходной информации часто называют потенциальными.
Статические (потенциальные) триггеры, в свою очередь, подразделяются на две неравные по практическому значению группы — симметричные и несимметричные триггеры. Оба класса реализуются на двухкаскадном усилителе с положительной обратной связью, а названием своим они обязаны способам организации внутренних электрических связей между элементами схемы.
Симметричные триггеры отличает симметрия схемы и по структуре, и по параметрам элементов обоих плеч. Для несимметричных триггеров характерна неидентичность параметров элементов отдельных каскадов, а также и связей между ними.
Симметричные статические триггеры составляют основную массу триггеров, используемых в современной радиоэлектронной аппаратуре. Схемы симметричных триггеров в простейшей реализации (2х2ИЛИНЕ) показаны на (рис. 2).
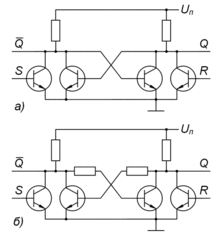
Рис. 2.
Симметричные триггеры:
а — с непосредственной связью между каскадами;
б — с резистивной связью
Основной и наиболее общий классификационный признак — функциональный – позволяет систематизировать статические симметричные триггеры по способу организации логических связей между входами и выходами триггера в определённые дискретные моменты времени до и после появления входных сигналов. По этой классификации триггеры характеризуются числом логических входов и их функциональным назначением (рис. 3).
Реклама

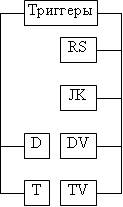
Рис. 3.
Функциональная классификация триггеров
Вторая классификационная схема, независимая от функциональной, характеризует триггеры по способу ввода информации и оценивает их по времени обновления выходной информации относительно момента смены информации на входах (рис. 4).

Рис. 4.
Классификация триггеров по способу ввода информации
Каждая из систем классификации характеризует триггеры по разным показателям и поэтому дополняет одна другую. К примеру, триггеры RS-типа могут быть в синхронном и асинхронном исполнении.
Асинхронный триггер изменяет своё состояние непосредственно в момент появления соответствующего информационного сигнала, с некоторой задержкой равной сумме задержек на элементах составляющих данный триггер.
Синхронные триггеры реагируют на информационные сигналы только при наличии соответствующего сигнала на так называемом входе синхронизации С (от англ. clock). Этот вход также обозначают термином «такт». Такие информационные сигналы называют синхронными. Синхронные триггеры в свою очередь подразделяют на триггеры со статическим (статические) и динамическим (динамические) управлением по входу синхронизации С.
Одноступенчатые триггеры состоят из одной ступени представляющей собой элемент памяти и схему управления, делятся на триггеры со статическим управлением и триггеры с динамическим управлением.
Триггеры со статическим управлением воспринимают информационные сигналы при подаче на вход С логической единицы (прямой вход) или логического нуля (инверсный вход).
Триггеры с динамическим управлением воспринимают информационные сигналы при изменении (перепаде) сигнала на входе С от 0 к 1 (прямой динамический С-вход) или от 1 к 0 (инверсный динамический С-вход). Также встречается название «триггер управляемый фронтом».
Двухступенчатые триггеры бывают, как правило, со статическим управлением. При одном уровне сигнала на входе С информация, в соответствии с логикой работы триггера, записывается в первую ступень (вторая ступень заблокирована для записи). При другом уровне этого сигнала происходит копирование состояния первой ступени во вторую (первая ступень заблокирована для записи), выходной сигнал появляется в этот момент времени с задержкой равной задержке срабатывания ступени. Обычно двухступенчатые триггеры применяются в схемах, где логические функции входов триггера зависят от его выходов, во избежание временных гонок. Двухступенчатые триггеры с динамическим управлением встречаются крайне редко. Двухступенчатый триггер обозначают ТТ.
Триггеры со сложной логикой бывают также одно- и двухступенчатые. В этих триггерах наряду с синхронными сигналами присутствуют и асинхронные. Такой триггер изображён на рис. 5, верхний (S) и нижний (R) входные сигналы являются асинхронными.

Рис. 5.
Схема RS-триггера двухступенчатого со сложной логикой на элементах 2И-НЕ и 3И-НЕ
В графе триггера каждая вершина графа соединена со всеми другими вершинами, при этом переходы от вершины к вершине возможны в обе стороны (двухсторонние). Граф двоичного триггера — две точки соединённые отрезком прямой линии, троичного триггера — треугольник, четверичного триггера — квадрат с диагоналями, пятеричного триггера — пятиугольник с пентаграммой и т. д. При N=1 граф триггера вырождается в одну точку, в математике ему соответствует унарная единица или унарный ноль, а в электронике — монтажная «1» или монтажный «0», то есть простейшее ПЗУ. Устойчивые состояния имеют на графе триггера дополнительную петлю, которая обозначает, что при снятии управляющих сигналов триггер остаётся в установленном состоянии.
Состояние триггера определяется сигналами на прямом и инверсном выходах. При положительном кодировании (позитивная логика) высокий уровень напряжения на прямом выходе отображает значение 1 (состояние = 1), а низкий уровень — значение 0 (состояние = 0). При отрицательном кодировании (негативная логика) высокому уровню (напряжению) соответствует логическое значение "0", а низкому уровню (напряжению) соответствует логическое значение "1".
Изменение состояния триггера (его переключение или запись) обеспечивается внешними сигналами и сигналами обратной связи, поступающими с выходов триггера на входы схемы управления (комбинационной схемы или входной логики). Обычно внешние сигналы, как и входы триггера, обозначают латинскими буквами R, S, T, C, D, V и др. В простейших схемах триггеров отдельная схема управления (КС) может отсутствовать. Поскольку функциональные свойства триггеров определяются их входной логикой, то названия основных входов переносятся на всю схему триггера.
Входы триггеров разделяются на информационные (R, S, T и др.) и управляющие (С, V). Информационные входы предназначены для приема сигналов запоминаемой информации. Названия входных сигналов отождествляют с названиями входов триггера. Управляющие входы служат для управления записью информации. В триггерах может быть два вида управляющих сигналов:
· синхронизирующий (тактовый) сигнал С, поступающий на С-вход (тактовый вход);
· разрешающий сигнал V, поступающий на V-вход.
На V-входы триггера поступают сигналы, которые разрешают (V=1) или запрещают (V=0) запись информации. В синхронных триггерах с V-входом запись информации возможна при совпадении сигналов на информационном С и V-входах.
Каждый тип триггера имеет собственную таблицу работы (таблицу истинности). Выходное состояние триггера обычно обозначают буквой Q. Индекс возле буквы означает состояние до подачи сигнала (t) или после подачи сигнала (t+1). В триггерах с парафазным (двухфазным) выходом имеется второй (инверсный) выход, который обозначают как Q, /Q или Q'.
Кроме табличного определения работы триггера существует формульное задание функции триггера в секвенциальной логике. Например, функцию RS-триггера в секвенциальной логике представляет формула 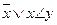 . Аналитическая запись SR-триггера выглядит так: . Аналитическая запись SR-триггера выглядит так: 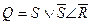 . .
1.1. Типы триггеров
1.1.1.
RS
-
триггеры
RS-триггер, или SR-триггер – триггер, который сохраняет своё предыдущее состояние при нулевых входах и меняет своё выходное состояние при подаче на один из его входов единицы. Граф RS-триггера показан на (рис. 6).
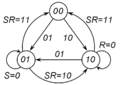
Рис. 6.
Граф переходов асинхронного RS-триггера
При подаче единицы на вход S (от англ. Set – установить) выходное состояние становится равным логической единице. А при подаче единицы на вход R (от англ. Reset – сбросить) выходное состояние становится равным логическому нулю. Состояние, при котором на оба входа R и S одновременно поданы логические единицы, в некоторых случаях является запрещённым, при такой комбинации RS-триггер переходит в третье состояние QQ=00. Одновременное снятие двух «1» практически невозможно. При снятии одной из «1» RS-триггер переходит в состояние, определяемое оставшейся «1». Таким образом RS-триггер имеет три состояния, из которых два устойчивых (при снятии сигналов управления RS-триггер остаётся в установленном состоянии) и одно неустойчивое (при снятии сигналов управления RS-триггер не остаётся в установленном состоянии, а переходит в одно из двух устойчивых состояний).
RS-триггер используется для создания сигнала с положительным и отрицательным фронтами, отдельно управляемыми посредством стробов, разнесённых во времени. Также RS-триггеры часто используются для исключения так называемого явления дребезга контактов.
RS-триггеры иногда называют RS-фиксаторами.
JK-триггеры
JK-триггер работает так же как RS-триггер, с одним лишь исключением: при подаче логической единицы на оба входа J и K состояние выхода триггера изменяется на противоположное. Вход J (от англ. Jump – прыжок) аналогичен входу S у RS-триггера. Вход K (от англ. Kill – убить) аналогичен входу R у RS-триггера. При подаче единицы на вход J и нуля на вход K выходное состояние триггера становится равным логической единице. А при подаче единицы на вход K и нуля на вход J выходное состояние триггера становится равным логическому нулю. JK-триггер в отличие от RS-триггера не имеет запрещённых состояний на основных входах, однако это никак не помогает при нарушении правил разработки логических схем. На практике применяются только синхронные JK-триггеры, то есть состояния основных входов J и K учитываются только в момент тактирования, например по положительному фронту импульса на входе синхронизации.
На базе JK-триггера возможно построить D-триггер или Т-триггер. Как можно видеть в таблице истинности JK-триггера, он переходит в инверсное состояние каждый раз при одновременной подаче на входы J и K логической 1. Это свойство позволяет создать на базе JK-триггера Т-триггер, объединив входы J и К.
| J
|
K
|
Q(t)
|
Q(t+1)
|
| 0
|
0
|
0
|
0
|
| 0
|
0
|
1
|
1
|
| 0
|
1
|
0
|
0
|
| 0
|
1
|
1
|
0
|
| 1
|
0
|
0
|
1
|
| 1
|
0
|
1
|
1
|
| 1
|
1
|
0
|
1
|
| 1
|
1
|
1
|
0
|
Табл. 1.
Таблица истинности JK-триггера
Алгоритм функционирования JK-триггера можно представить формулой:
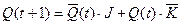 . (фор.1) . (фор.1)
2. Полусумматоры
Полусумматор — логическая схема имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S,C, где S — это бит суммы по модулю, а C — бит переноса. Однако, как можно заметить, для построения схемы двоичного сумматора (трёхразрядный сумматор, тринарный сумматор) необходимо иметь элемент, который суммирует три бита A, B и C, где C — бит переноса из предыдущего разряда, таким элементом является полный двоичный сумматор, который как правило состоит из двух полусумматоров и логического элемента 2ИЛИ (рис. 7).

Рис. 7.
Двоичный полусумматор
3. Сумматоры

Рис. 8.
Сумматор
Сумматор – логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учет знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.
Допустим, требуется сложить двоичные числа 1001 и 0011. Сначала складываем младшие разряды (последние цифры): 1+1=10. Т.е. в младшем разряде будет 0, а единица – это перенос в старший разряд. Далее: 0 + 1 + 1(от переноса) = 10, т.е. в данном разряде снова запишется 0, а единица уйдет в старший разряд. На третьем шаге: 0 + 0 + 1(от переноса) = 1. В итоге сумма равна 1100.
Сумматоры классифицируют по различным признакам.
В зависимости от системы счисления различают:
· двоичные;
· двоично-десятичные (в общем случае двоично-кодированные;
· десятичные;
· прочие (например, амплитудные).
По количеству одновременно обрабатываемых разрядов складываемых чисел:
· одноразрядные;
· многоразрядные.
По числу входов и выходов одноразрядных двоичных сумматоров:
· четвертьсумматоры (элементы "сумма по модулю 2"; элементы "исключающее ИЛИ"), характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;
· полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноименные разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом перенос в следующий (более старший разряд);
· полные одноразрядные двоичные сумматоры, характеризующиеся наличием трех входов, на которые подаются одноименные разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом перенос в следующий (более старший разряд).
По способу представления и обработки складываемых чисел многоразрядные сумматоры подразделяются на:
· последовательные, в которых обработка чисел ведется поочередно, разряд за разрядом на одном и том же оборудовании;
· параллельные, в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется свое оборудование.
Параллельный сумматор в простейшем случае представляет собой n одноразрядных сумматоров, последовательно (от младших разрядов к старшим) соединенных цепями переноса. Однако такая схема сумматора характеризуется сравнительно невысоким быстродействием, так как формирование сигналов суммы и переноса в каждом i-ом разряде производится лишь после того, как поступит сигнал переноса с (i-1)-го разряда. Таким образом, быстродействие сумматора определяется временем распространения сигнала по цепи переноса. Уменьшение этого времени основная задача при построении параллельных сумматоров.
Для уменьшения времени распространения сигнала переноса применяют: конструктивные решения, когда используют в цепи переноса наиболее быстродействующие элементы; тщательно выполняют монтаж без длинных проводников и паразитных емкостных составляющих нагрузки и (наиболее часто) структурные методы ускорения прохождения сигнала переноса.
По способу организации межразрядных переносов параллельные сумматоры, реализующие структурные методы, делят на сумматоры:
· с последовательным переносом;
· с параллельным переносом;
· с групповой структурой;
· со специальной организацией цепей переноса.
По способу выполнения операции сложения и возможности сохранения результата сложения можно выделить три основных вида сумматоров:
· комбинационный, выполняющий микрооперацию "S = A плюс B", в котором результат выдается по мере его образования (это комбинационная схема в общепринятом смысле слова);
· сумматор с сохранением результата "S = A плюс B";
· накапливающий, выполняющий микрооперацию "S = S плюс B".
Последние две структуры строятся либо на счетных триггерах (сейчас практически не используются), либо по структуре "комбинационный сумматор регистр хранения" (сейчас наиболее употребляемая схема).
Важнейшими параметрами сумматоров являются:
· разрядность;
· статические параметры: Uвх, Uвх, Iвх и так далее, то есть обычные параметры интегральных схем;
· динамические параметры. Сумматоры характеризуются четырьмя задержками распространения;
· от подачи входного переноса до установления всех выходов суммы при постоянном уровне на всех входах слагаемых;
· от одновременной подачи всех слагаемых до установления всех выходов суммы при постоянном уровне на входе переноса;
· от подачи входного переноса до установления выходного переноса при постоянном уровне на входах слагаемых;
· от подачи всех слагаемых до установления выходного переноса при постоянном уровне на входах слагаемых.
4. Счётчики
Счётчик числа импульсов – устройство, на выходах которого получается двоичный (двоично-десятичный) код, определяемый числом поступивших импульсов. Счётчики могут строиться на T-триггерах. Основной параметр счётчика – модуль счёта – максимальное число единичных сигналов, которое может быть сосчитано счётчиком. Счётчики обозначают через СТ (от англ. counter).
Счётчики классифицируют:
1) по числу устойчивых состояний триггеров:
· на двоичных триггерах;
· на троичных триггерах;
· на n-ичных триггерах.
2) по модулю счёта:
· двоично-десятичные (декада);
· двоичные;
· с произвольным постоянным модулем счёта;
· с переменным модулем счёта.
3) по направлению счёта:
· суммирующие;
· вычитающие;
· реверсивные.
4) по способу формирования внутренних связей:
· с последовательным переносом;
· с параллельным переносом;
· с комбинированным переносом;
· кольцевые.
5) по способу переключения триггера:
· синхронные;
· асинхронные.
Схему двоичного счетчика можно получить с помощью формального синтеза, однако более наглядным путем представляется эвристический. Таблица истинности двоичного счетчика — последовательность двоичных чисел от нуля до 2n − 1, где n - разрядность счётчика. Наблюдение за разрядами чисел, составляющих таблицу, приводит к пониманию структурной схемы двоичного счетчика. Состояния младшего разряда при его просмотре по соответствующему столбцу таблицы показывают чередование нулей и единиц вида 01010101..., что естественно, т. к. младший разряд принимает входной сигнал и переключается от каждого входного воздействия. В следующем разряде наблюдается последовательность пар нулей и единиц вида 00110011... . В третьем разряде образуется последовательность из четверок нулей и единиц 00001111... и т.д. Из этого наблюдения видно, что следующий по старшинству разряд переключается с частотой, в два раза меньшей, чем данный. Известно, что счетный триггер делит частоту входных импульсов на два. , Сопоставив этот факт с указанной выше закономерностью, видим, что счетчик может быть, построен в виде цепочки последовательно включенных счетных триггеров. Заметим, кстати, что согласно ГОСТу входы элементов изображаются слева, а выходы справа. Соблюдение этого правила ведет к тому, что в числе, содержащемся в счетчике, младшие разряды расположены левее старших.
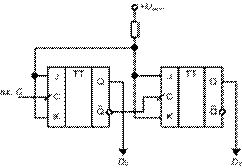
Рис. 9.
Двухразрядный двоичный счётчик с последовательной организацией переноса на T-триггере.
5. Регистры
Регистр – последовательное логическое устройство, используемое для хранения n-разрядных двоичных слов (чисел) и выполнения преобразований над ними.
Регистр представляет собой упорядоченную последовательность триггеров, число которых соответствует числу разрядов в слове. С каждым регистром обычно связано комбинационное цифровое устройство, с помощью которого обеспечивается выполнение некоторых операций над словами.
Фактически любое цифровое устройство можно представить в виде совокупности регистров, соединённых друг с другом при помощи комбинационных цифровых устройств.
Основой построения регистров являются D-триггеры, RS-триггеры.
Регистры классифицируются по следующим видам:
· накопительные (регистры памяти, хранения);
· сдвигающие.
В свою очередь сдвигающие регистры делятся:
1) по способу ввода-вывода информации:
· параллельные – запись и считывание информации происходит одновременно на все входы и со всех выходов;
· последовательные – запись и считывание информации происходит в первый триггер, а та информация, которая была в этом триггере, перезаписывается в следующий - то же самое происходит и с остальными триггерами;
· комбинированные.
2) по направлению передачи информации:
· однонаправленные;
· реверсивные.
Регистром называется функциональный узел, осуществляющий приём, хранение и передачу информации. Регистры состоят из группы триггеров, обычно D. По типу приёма и выдачи информации различают 3 типа регистров:
· С последовательным приёмом и выдачей информации — сдвиговые регистры;
· С параллельным приёмом и выдачей информации — параллельные регистры;
· С параллельно-последовательным приёмом и выдачей информации.
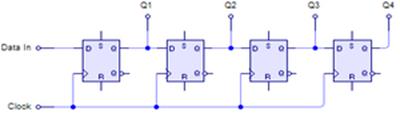
Рис. 10.
4-х разрядный сдвиговый регистр, преобразователь последовательного кода в параллельный и обратно
6.Шифратор
Шифратор (кодер) преобразует единичный сигнал на одном из входов в n-разрядный двоичный код. Наибольшее применение он находит в устройствах ввода информации (пультах управления) для преобразования десятичных чисел в двоичную систему счисления. Предположим, на пульте десять клавиш с гравировкой от 0 до 9. При нажатии любой из них на вход шифратора подается единичный сигнал ( ). На выходе шифратора должен появиться двоичный код ( ). На выходе шифратора должен появиться двоичный код (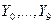 )этого десятичного числа. Как видно из таблицы истинности (табл. 2), в этом случае нужен преобразователь с десятью входами и четырьмя выходами. )этого десятичного числа. Как видно из таблицы истинности (табл. 2), в этом случае нужен преобразователь с десятью входами и четырьмя выходами.
| Входы
|
Выходы
|
| X
|
Y3
|
Y2
|
Y1
|
Y0
|
| 0
|
0
|
0
|
0
|
0
|
| 1
|
0
|
0
|
0
|
1
|
| 2
|
0
|
0
|
1
|
0
|
| 3
|
0
|
0
|
1
|
1
|
| 4
|
0
|
1
|
0
|
0
|
| 5
|
0
|
1
|
0
|
1
|
| 6
|
0
|
1
|
1
|
0
|
| 7
|
0
|
1
|
1
|
1
|
| 8
|
1
|
0
|
0
|
0
|
| 9
|
1
|
0
|
0
|
1
|
Табл. 2.
Таблица истинности
7. Дешифратор
Дешифратор (декодер) – комбинационное устройство, преобразующее n-разрядный двоичный, троичный или k-ичный код в 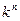 -ичный одноединичный код, где k - основание системы счисления. Логический сигнал появляется на том выходе, порядковый номер которого соответствует двоичному, троичному или k-ичному коду. -ичный одноединичный код, где k - основание системы счисления. Логический сигнал появляется на том выходе, порядковый номер которого соответствует двоичному, троичному или k-ичному коду.
Дешифраторы являются устройствами, выполняющими двоичные, троичные или k-ичные логические функции (операции).
Часто дешифраторы дополняются входом разрешения работы E. Если на этот вход поступает единица, то дешифратор функционирует, в ином случае на выходе дешифратора вырабатывается логический ноль вне зависимости от входных сигналов.
Существуют дешифраторы с инверсными выходами, у такого дешифратора выбранный разряд показан нулём.
Функционирование дешифратора описывается системой конъюнкций:
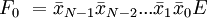
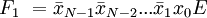
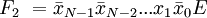
…………………………………………………………
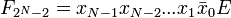
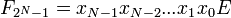
Обратное преобразование осуществляет шифратор.
Дешифраторы - это комбинационные схемы с несколькими входами и выходами, преобразующие код, подаваемый на входы в сигнал на одном из выходов. На выходе дешифратора появляется логическая единица, на остальных — логические нули, когда на входных шинах устанавливается двоичный код определённого числа или символа, то есть дешифратор расшифровывает число в двоичном, троичном или k-ичном коде, представляя его логической единицей на определённом выходе. Число входов дешифратора равно количеству разрядов поступающих двоичных, троичных или k-ичных чисел. Число выходов равно полному количеству различных двоичных, троичных или k-ичных чисел этой разрядности.
Для n-разрядов на входе, на выходе 2n, 3n или kn. Чтобы вычислить, является ли поступившее на вход двоичное, троичное или k-ичное число известным ожидаемым, инвертируются пути в определённых разрядах этого числа. Затем выполняется конъюнкция всех разрядов преобразованного таким образом числа. Если результатом конъюнкции является логическая единица, значит на вход поступило известное ожидаемое число.
Из логических элементов являющихся дешифраторами можно строить дешифраторы на большое число входов. Каскадное подключение таких схем позволит наращивать число дифференцируемых переменных.

Рис. 11.
Пример дешифратора 2×4
Заключение
В ходе данной работы были достигнуты поставленные цели рассмотрения логических устройств применяемых в ЭВМ, как они устроены и функционируют.
Триггеры подразделяются на две большие группы — динамические и статические. Названы они так по способу представления выходной информации. Статические (потенциальные) триггеры, в свою очередь, подразделяются на две неравные по практическому значению группы — симметричные и несимметричные триггеры. Оба класса реализуются на двухкаскадном усилителе с положительной обратной связью, а названием своим они обязаны способам организации внутренних электрических связей между элементами схемы. Статистические триггеры могут классифицироваться двумя способами: функциональный и по вводу информации.
Полусумматор — логическая схема имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров.
Сумматор – логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. Сумматоры классифицируют по системе счисления, одновременно обрабатываемых разрядов складываемых чисел, числу входов и выходов одноразрядных двоичных сумматоров, способу представления и обработки складываемых чисел.
Счётчик числа импульсов – устройство, на выходах которого получается двоичный (двоично-десятичный) код, определяемый числом поступивших импульсов. Счётчики классифицируются по числу устойчивых состояний триггеров, модулю счёта, направлению счёта, способу формирования внутренних связей, способу переключения триггера.
Регистр – последовательное логическое устройство, используемое для хранения n-разрядных двоичных слов (чисел) и выполнения преобразований над ними. Регистры классифицируются на накопительные и сдвигающие. Вторые же – по способу ввода-вывода информации и направлению передачи информации.
Шифратор (кодер) преобразует единичный сигнал на одном из входов в n-разрядный двоичный код. Наибольшее применение он находит в устройствах ввода информации (пультах управления) для преобразования десятичных чисел в двоичную систему счисления.
Дешифратор (декодер) – комбинационное устройство, преобразующее n-разрядный двоичный, троичный или k-ичный код в 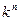 -ичный одноединичный код, где k - основание системы счисления. Из логических элементов являющихся дешифраторами можно строить дешифраторы на большое число входов. Каскадное подключение таких схем позволит наращивать число дифференцируемых переменных. -ичный одноединичный код, где k - основание системы счисления. Из логических элементов являющихся дешифраторами можно строить дешифраторы на большое число входов. Каскадное подключение таких схем позволит наращивать число дифференцируемых переменных.
Список используемой литературы
1. Зельдин Е.А. Цифровые интегральные микросхемы в информационно-измерительной аппаратуре. – Л.: Энергоатомиздат. Ленингр. отд-ние, 1986. – 280 с.
2. Каган Б.Н. Электронные вычислительные машины и системы: Учеб. пособие для вузов. – 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1985. – 552 с.
3. Шило В.А. Популярные цифровые микросхемы: Справочник. – Челябинск: Металлургия, Челябинское отделение, 1988. – 352 с.
4. Микропроцессоры и микропроцессорные комплекты интегральных микросхем: Справочник: В 2 Т. / Н.Н. Аверьянов, А.И. Березенко, Ю.И. Борщенко и др.; Под редакцией В.А. Шехнова. – М.: Радио и связь, 1988. – Т.2. – 368 с.
5. Соломатин Н.М. Логические элементы ЭВМ. М.: Высш. шк., 2000. - 160 с.
6. Букреев И.Н., Горячев В.И., Мансуров Б.М. Микроэлектронные схемы цифровых устройств. М.: Радио и связь, 2000. - 416 с.
|