Министерство образования Российской Федерации
Иркутский Государственный Технический Университет
Кафедра мировой экономики
Контрольная работа по статистике
Иркутск 2007
Анализ рядов динамики
Потребление мясопродуктов на одного члена семьи, кг/год.
| Продукты |
1970 |
1975 |
1980 |
1985 |
1990 |
1995 |
2000 |
2005 |
| Мясо и мясопродукты |
85,6 |
83,9 |
80 |
78,4 |
74,1 |
68,3 |
58,7 |
63,2 |
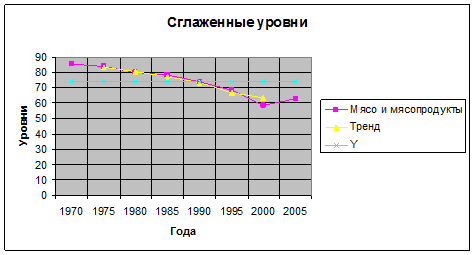
Представим исходные уровни ряда динамики в виде диаграммы.
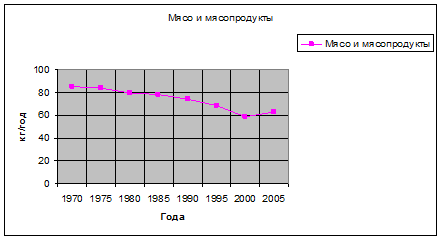
Для анализа потребления мясопродуктов требуется определить относительные величины динамики.
1) Абсолютные приросты изменения уровня (цепные и базисные)
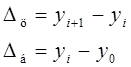
где 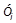 — уровень изучаемого периода; — уровень изучаемого периода; 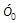 — базисный уровень. — базисный уровень.
2) Для выявления характера изменений потребления мясопродуктов по отдельным периодам экономического развития произведем расчет темпов роста(цепные и базисные).
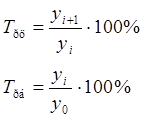
3) Темпы прироста (цепные и базисные)

4) Абсолютное значение 1% прироста (только для цепных показателей)

5) Средний уровень ряда
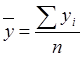
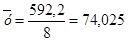
| абс.прирост |
темп роста |
темп прироста |
абс знач прир 1% |
| Год |
базисный |
цепной |
базисный |
цепной |
базисный |
цепной |
| 1970 |
- |
- |
- |
- |
- |
- |
- |
| 1975 |
-1,7 |
-1,7 |
98,01% |
98,01% |
-1,99% |
-1,99% |
85,6 |
| 1980 |
-5,6 |
-3,9 |
93,46% |
95,35% |
-6,54% |
-4,65% |
83,9 |
| 1985 |
-7,2 |
-1,6 |
91,59% |
98,00% |
-8,41% |
-2,00% |
80 |
| 1990 |
-11,5 |
-4,3 |
86,57% |
94,52% |
-13,43% |
-5,48% |
78,4 |
| 1995 |
-17,3 |
-5,8 |
79,79% |
92,17% |
-20,21% |
-7,83% |
74,1 |
| 2000 |
-26,9 |
-9,6 |
68,57% |
85,94% |
-31,43% |
14,06% |
68,3 |
| 2005 |
-22,4 |
4,5 |
73,83% |
107,67% |
-26,17% |
7,67% |
58,7 |
Из полученных базисных относительных величин динамики (темпов роста) видно, что за указанные годы потребление мясопродуктов на одного члена семьи неуклонно возрастало.
Из полученных цепных относительных величин динамики (темпов роста) видно, что по отдельным этапам экономического развития также происходило увеличение потребления.
Сглаживание ряда динамики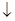
| Год
|
Мясо и мясопродукты
|
Тренд
|
Y
|
| 1970 |
85,6 |
74,025 |
| 1975 |
83,9 |
83,16667 |
74,025 |
| 1980 |
80 |
80,76667 |
74,025 |
| 1985 |
78,4 |
77,5 |
74,025 |
| 1990 |
74,1 |
73,6 |
74,025 |
| 1995 |
68,3 |
67,03333 |
74,025 |
| 2000 |
58,7 |
63,4 |
74,025 |
| 2005 |
63,2 |
74,025 |
Аналитическое выравнивание
| Год |
y
|
t
|
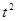
|
yt
|

|

|
| 1970 |
85,6 |
1 |
1 |
85,6 |
87,450 |
3,423 |
| 1975 |
83,9 |
2 |
4 |
167,8 |
83,614 |
0,082 |
| 1980 |
80 |
3 |
9 |
240 |
79,779 |
0,049 |
| 1985 |
78,4 |
4 |
16 |
313,6 |
75,943 |
6,038 |
| 1990 |
74,1 |
5 |
25 |
370,5 |
72,107 |
3,971 |
| 1995 |
68,3 |
6 |
36 |
409,8 |
68,271 |
0,001 |
| 2000 |
58,7 |
7 |
49 |
410,9 |
64,436 |
32,898 |
| 2005 |
63,2 |
8 |
64 |
505,6 |
60,600 |
6,760 |
| Итого |
592,2 |
36 |
204 |
2503,8 |
592,200 |
53,221 |
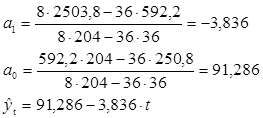 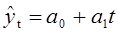
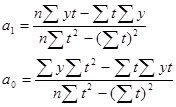
| Год
|
Уровни
|
Y |
Тренд
|
| 1970 |
87,45 |
74,025 |
| 1975 |
83,61428571 |
74,025 |
83,166 |
| 1980 |
79,77857143 |
74,025 |
80,766 |
| 1985 |
75,94285714 |
74,025 |
77,5 |
| 1990 |
72,10714286 |
74,025 |
73,6 |
| 1995 |
68,27142857 |
74,025 |
67,033 |
| 2000 |
64,43571429 |
74,025 |
63,4 |
| 2005 |
60,6 |
74,025 |

Измерение колебаний в рядах динамики
| Год
|
Мясо и мясопродукты
|
у-ср у
|
у-тренд
|
| 1970 |
85,6 |
11,575 |
85,600 |
| 1975 |
83,9 |
9,875 |
0,733 |
| 1980 |
80 |
5,975 |
-0,767 |
| 1985 |
78,4 |
4,375 |
0,900 |
| 1990 |
74,1 |
0,075 |
0,500 |
| 1995 |
68,3 |
-5,725 |
1,267 |
| 2000 |
58,7 |
-15,325 |
-4,700 |
| 2005 |
63,2 |
-10,825 |
63,200 |
| Итого |
0,00 |
146,733 |
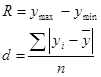
| Года |
Мясо и мясопродукты |
Тренд |
y - тренд |
у -средняя |
| 1970 |
85,6 |
83,166667 |
2,43333333 |
11,575 |
5,921111 |
133,9806 |
| 1975 |
83,9 |
80,766667 |
3,13333333 |
9,875 |
9,817778 |
97,51563 |
| 1980 |
80 |
77,5 |
2,5 |
5,975 |
6,25 |
35,70062 |
| 1985 |
78,4 |
73,6 |
4,8 |
4,375 |
23,04 |
19,14063 |
| 1990 |
74,1 |
67,033333 |
7,06666667 |
0,075 |
49,93778 |
0,005625 |
| 1995 |
68,3 |
63,4 |
4,9 |
5,725 |
24,01 |
32,77563 |
| 2000 |
58,7 |
58,7 |
15,325 |
3445,69 |
234,8556 |
| 2005 |
63,2 |
63,2 |
10,825 |
3994,24 |
117,1806 |
| Итого |
146,733333 |
63,75 |
7558,907 |
671,155 |
| средняя |
макс |
63,2 |
макс |
15,325 |
| 74,025 |
мин |
2,4333333 |
мин |
0,075 |
| R |
60,766667 |
R |
15,25 |
| d |
18,341667 |
d |
7,96875 |
| G |
944,86333 |
G |
83,894375 |
| V |
1276,41% |
V |
113,33% |
Определение сумм квадратов отклонений
| Года |
y
|
yi-y
|
(yi-y)2
|
y1t-y
|
(y1t-y)2
|
yi-y1t
|
(yi-y1t)2
|
| 1970 |
85,6 |
11,575 |
133,981 |
13,425 |
180,231 |
-1,850 |
3,423 |
| 1975 |
83,9 |
9,875 |
97,516 |
9,589 |
91,954 |
0,286 |
0,082 |
| 1980 |
80 |
5,975 |
35,701 |
5,754 |
33,104 |
0,221 |
0,049 |
| 1985 |
78,4 |
4,375 |
19,141 |
1,918 |
3,678 |
2,457 |
6,038 |
| 1990 |
74,1 |
0,075 |
0,006 |
-1,918 |
3,678 |
1,993 |
3,971 |
| 1995 |
68,3 |
-5,725 |
32,776 |
-5,754 |
33,104 |
0,029 |
0,001 |
| 2000 |
58,7 |
-15,325 |
234,856 |
-9,589 |
91,954 |
-5,736 |
32,898 |
| 2005 |
63,2 |
-10,825 |
117,181 |
-13,425 |
180,231 |
2,600 |
6,760 |
| Итого |
592,2 |
671,155 |
617,934 |
53,221 |
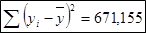
Среднеквадратическая ошибка уравнения тренда:

Выявление изменений сезонных колебаний
| Года |
y
|
Iсез
|
Yi-Y
|
Yi-Y/Y*100%
|
(Iсез-100%)2
|
(Yi-Y)2
|
| 1970 |
85,6 |
115,637% |
11,575 |
15,637% |
0,024 |
133,981 |
| 1975 |
83,9 |
113,340% |
9,875 |
13,340% |
0,018 |
97,516 |
| 1980 |
80 |
108,072% |
5,975 |
8,072% |
0,007 |
35,701 |
| 1985 |
78,4 |
105,910% |
4,375 |
5,910% |
0,003 |
19,141 |
| 1990 |
74,1 |
100,101% |
0,075 |
0,101% |
0,000 |
0,006 |
| 1995 |
68,3 |
92,266% |
-5,725 |
-7,734% |
0,006 |
32,776 |
| 2000 |
58,7 |
79,298% |
-15,325 |
-20,702% |
0,043 |
234,856 |
| 2005 |
63,2 |
85,377% |
-10,825 |
-14,623% |
0,021 |
117,181 |
| Итого |
592,2 |
800,000% |
0,00 |
0,000 |
0,122 |
671,155 |
Задание 1
| Основные фонды, тыс.руб.
|
Продукция, тыс.руб.
|
Число рабочих, чел.
|
Средняя выработка продукции
|
Основные фонды, тыс.руб.
|
Продукция, тыс.руб.
|
Число рабочих, чел.
|
| 5 |
3150 |
2390 |
163 |
14,663 |
3350 |
2310 |
159 |
| 6 |
5150 |
2750 |
178 |
15,449 |
5290 |
2980 |
180 |
| 7 |
4710 |
2500 |
167 |
14,970 |
4650 |
2850 |
170 |
| 8 |
4940 |
2810 |
180 |
15,611 |
4610 |
2950 |
173 |
| 10 |
6820 |
3630 |
208 |
17,452 |
7290 |
4100 |
200 |
| 13 |
6900 |
3950 |
205 |
19,268 |
7500 |
4480 |
192 |
| 17 |
8820 |
5190 |
219 |
23,699 |
9050 |
5430 |
209 |
| 18 |
9350 |
5740 |
230 |
24,957 |
9800 |
6040 |
235 |
| 19 |
9810 |
5590 |
225 |
24,844 |
10320 |
6100 |
240 |
| 23 |
10970 |
6150 |
239 |
25,732 |
11370 |
6540 |
242 |
| 24 |
11050 |
5850 |
236 |
24,788 |
11420 |
6460 |
266 |
| 25 |
11190 |
6750 |
229 |
29,476 |
11350 |
7130 |
240 |
| 26 |
11240 |
6940 |
234 |
29,658 |
11590 |
7350 |
241 |
| 30 |
12090 |
6750 |
232 |
29,095 |
12310 |
6960 |
230 |
| 31 |
12410 |
6820 |
240 |
28,417 |
12650 |
7090 |
246 |
| 33 |
13150 |
6980 |
242 |
28,843 |
13430 |
7680 |
250 |
| 38 |
14300 |
7900 |
250 |
31,600 |
15850 |
8390 |
261 |
| 40 |
14770 |
7860 |
251 |
31,315 |
15030 |
8390 |
262 |
| 41 |
14800 |
7700 |
260 |
29,615 |
15280 |
8100 |
269 |
| 42 |
14980 |
7810 |
264 |
29,583 |
15460 |
8410 |
286 |
| 43 |
15320 |
8090 |
280 |
28,893 |
15840 |
8810 |
290 |
| 45 |
15870 |
8480 |
290 |
29,241 |
16670 |
8900 |
291 |
| 47 |
16810 |
8450 |
324 |
26,080 |
17530 |
9250 |
345 |
| 48 |
17340 |
9290 |
330 |
28,152 |
17600 |
9610 |
341 |
| 50 |
18310 |
10560 |
365 |
28,932 |
18910 |
11000 |
375 |
| Итого |
284250 |
156930 |
6041 |
25,977 |
294150 |
167310 |
6193 |
Задание 2

где 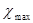 и и 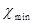 - максимальное и минимальное значения стоимости основных фондов, - максимальное и минимальное значения стоимости основных фондов,
n - число групп.
Образуем четыре группы заводов. Тогда величина интервала равна:
i
=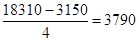
Теперь образуем группы заводов, которые отличаются друг от друга по стоимости основных фондов на эту величину.
| Основные фонды, тыс.руб.
|
Группы
|
| 3150-6940 |
1-ая
|
| 6940-10730 |
2-ая
|
| 10730-14520 |
3-я
|
| 14520-18310 |
4-ая
|
На основании этого составляем таблицу, в которой показываем распределение заводов по размеру основных фондов, продукции, числу рабочих, средней выработки продукции.
| Завод
|
2002 г.
|
| Основные фонды, тыс.руб.
|
Продукция, тыс.руб.
|
Число рабочих, чел.
|
Средняя выработка продукции
|
Группы
|
| 5 |
3150 |
2390 |
163 |
14,663 |
1-ая
|
| 6 |
5150 |
2750 |
178 |
15,449 |
| 7 |
4710 |
2500 |
167 |
14,970 |
| 8 |
4940 |
2810 |
180 |
15,611 |
| 10 |
6820 |
3630 |
208 |
17,452 |
| 13 |
6900 |
3950 |
205 |
19,268 |
| 17 |
8820 |
5190 |
219 |
23,699 |
2-ая
|
| 18 |
9350 |
5740 |
230 |
24,957 |
| 19 |
9810 |
5590 |
225 |
24,844 |
| 23 |
10970 |
6150 |
239 |
25,732 |
3-я
|
| 24 |
11050 |
5850 |
236 |
24,788 |
| 25 |
11190 |
6750 |
229 |
29,476 |
| 26 |
11240 |
6940 |
234 |
29,658 |
| 30 |
12090 |
6750 |
232 |
29,095 |
| 31 |
12410 |
6820 |
240 |
28,417 |
| 33 |
13150 |
6980 |
242 |
28,843 |
| 38 |
14300 |
7900 |
250 |
31,600 |
| 40 |
14770 |
7860 |
251 |
31,315 |
4-ая
|
| 41 |
14800 |
7700 |
260 |
29,615 |
| 42 |
14980 |
7810 |
264 |
29,583 |
| 43 |
15320 |
8090 |
280 |
28,893 |
| 45 |
15870 |
8480 |
290 |
29,241 |
| 47 |
16810 |
8450 |
324 |
26,080 |
| 48 |
17340 |
9290 |
330 |
28,152 |
| 50 |
18310 |
10560 |
365 |
28,932 |
| Итого |
284250 |
156930 |
6041 |
25,977 |
По этим данным хорошо видно изменение стоимости основных фондов и легко обозначить границы групп.
Составим таблицу с системой показателей, куда занесем результаты группировки заводов по стоимости основных фондов.
| Основные фонды, тыс.руб. 2002г.
|
Группы
|
Число предприятий
|
Среднегодовая стоимость ОФ (всего)
|
Среднегодовая стоимость ОФ (на одно пред.)
|
Объем продукции (всего)
|
Объем продукции (на одно пред.)
|
Численность рабочих
|
Производительность труда одного рабочего
|
| 3150-6940 |
1-ая
|
6 |
31670 |
5278,333 |
18030 |
16,376 |
1101 |
16,376 |
| 6940-10730 |
2-ая
|
3 |
27980 |
9326,667 |
16520 |
24,510 |
674 |
24,510 |
| 10730-14520 |
3-я
|
8 |
96400 |
12050,000 |
54140 |
28,465 |
1902 |
28,465 |
| 14520-18310 |
4-ая
|
8 |
128200 |
16025,000 |
68240 |
28,866 |
2364 |
28,866 |
| Итого
|
25 |
284250 |
11370,000 |
156930 |
25,977 |
6041 |
25,977 |
Видно, что для данной отрасли характерной является группа заводов с основными фондами от 14520 до 18310 тыс. руб., которая имеет максимальные значения по всем показателям.
Реклама

Таким образом, в отличие от ряда распределения группировка позволяет сделать конкретные и содержательные выводы. Данная группировка показывает, что наиболее крупные предприятия имеют лучшие производственные показатели. Около 16 предприятий (группы 3 и 4) имеют больше всех основных фондов и дают максимальный объем промышленной продукции, имея около 60% общего числа рабочих.
Группировка эта произведена простая
, так как была выполнена по одному признаку, а так же аналитическая (факторная)
, поскольку устанавливает связь между взаимодействующими признаками – факторным и результативным. Чем больше основные фонды (результативный признак), тем больше среднегодовая стоимость основных фондов как на одно предприятие, так и всего (факторный признак), а также увеличивается объем продукции (всего) и производительность труда одного рабочего.
Задание 3
| Группы
|
Основные фонды, тыс.руб.
|
Численность рабочих, Fi
|
Середина интервала, Хi
|
ХiFi
|
Накопленные частоты, S
|
| 1-ая
|
3150-6940 |
1101 |
6620 |
7288620 |
1101 |
| 2-ая
|
6940-10730 |
674 |
12305 |
8293570 |
1775 |
| 3-я
|
10730-14520 |
1902 |
17990 |
34216980 |
3677 |
| 4-ая
|
14520-18310 |
2364 |
23675 |
55967700 |
6041 |
| Итого
|
6041 |
105766870 |

|
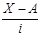
|

|
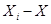
|
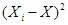
|
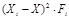
|
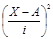
|

|
| -17055 |
-4,5 |
-4954,5 |
-10888,172 |
118552300 |
130526082441,38 |
20,25 |
22295,25 |
| -11370 |
-3 |
-2022 |
-5203,172 |
27073003,9 |
18247204655,47 |
9 |
6066 |
| -5685 |
-1,5 |
-2853 |
481,828 |
232157,751 |
441564043,01 |
2,25 |
4279,5 |
| 0 |
0 |
0 |
6166,828 |
38029761,6 |
89902356334,40 |
0 |
0 |
| -9829,5 |
-9442,690 |
239117207474,27 |
32640,75 |
Имеющиеся показатели и расчетные показатели
| h
|
3790 |
X
|
17508,172 |
| X
o
|
14520 |
Mo
|
15139,597 |
| F1
|
2364 |
Me
|
13211,832 |
| F2
|
1902 |
m1
|
-1,627 |
| F3
|
0 |
X
|
17508,172 |
| F/2
|
3020,5 |
G2
|
39582388,259 |
| Sme-1
|
1775 |
G
|
6291,454 |
| Fme
|
1902 |
m2
|
5,403 |
| Xme
|
10730 |
G2
|
39582388,259 |
| i
|
3790 |
G
|
6291,454 |
| A
|
23675 |
V
|
35,9% |
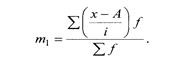
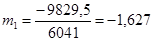
1 способ «способ моментов»:
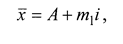

2 способ:
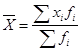
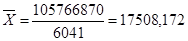
2) 1способ:
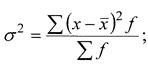
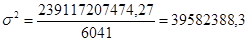
2 способ «способ моментов»:

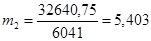
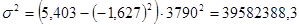
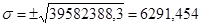
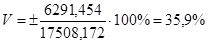

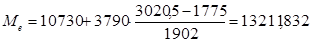
Задание 4
| Завод
|
2003 г.
|
| Основные фонды, тыс.руб.
|
Продукция, тыс.руб.
|
Число рабочих, чел.
|
Средняя выработка продукции
|
| 5 |
3350 |
2310 |
159 |
14,528 |
| 6 |
5290 |
2980 |
180 |
16,556 |
| 7 |
4650 |
2850 |
170 |
16,765 |
| 8 |
4610 |
2950 |
173 |
17,052 |
| 10 |
7290 |
4100 |
200 |
20,500 |
| 13 |
7500 |
4480 |
192 |
23,333 |
| 17 |
9050 |
5430 |
209 |
25,981 |
| 18 |
9800 |
6040 |
235 |
25,702 |
| 19 |
10320 |
6100 |
240 |
25,417 |
| 23 |
11370 |
6540 |
242 |
27,025 |
| Итого
|
73230 |
43780,000 |
2000 |
212,858 |
| ср. выработка |
21,286 |
| Выборка выше средней
|
Число рабочих
|
Удельный вес
|
| 127,458 |
1118 |
0,559 |
| удел. вес |
0,559 |
| G2 |
20,024 |
| хсред |
21,286 |
| под корнем |
0,015 |
| дельта х |
2,192 |
| границы |
23,478 |
| 19,094 |
| дельта омега |
0,122 |
| границы |
0,681 |
| 0,437 |
Задание 5
| 2002 |
2003 |
| Группы
|
Численность рабочих, fo
|
Выработка продукции,Xo
|
XoFo
|
Численность рабочих, F1
|
Выработка продукции,X1
|
X1F1
|
XoF1
|
| 1-ая
|
1101 |
97,413 |
107251,713 |
1074 |
108,734 |
116780,316 |
104621,562 |
| 2-ая
|
674 |
73,5 |
49539 |
684 |
77,1 |
52736,400 |
50274,000 |
| 3-я
|
1902 |
227,609 |
432912,318 |
1876 |
233,464 |
437978,464 |
426994,484 |
| 4-ая
|
2364 |
231,811 |
548001,204 |
2459 |
236,83 |
582364,970 |
570023,249 |
| Итого
|
6041 |
630,333 |
1137704,24 |
6093 |
656,128 |
1189860,150 |
1151913,295 |
При анализе объема продукции строится система общих индексов в агрегатной форме:

Первый индекс показывает изменение объема продукции по всем предприятиям вследствие влияния двух факторов: 1) численности рабочих; 2) производительности труда в каждой группе.
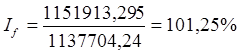
Этот индекс показывает изменение объема продукции за счет влияния численности рабочих.

А этот индекс показывает изменение объема продукции за счет влияния производительности труда в каждой группе.
Между этими индексами существует следующая взаимосвязь, которая позволяет проверить правильность расчетов:

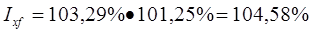
Разность между числителем и знаменателем индексов позволяет определить абсолютное изменение объема продукции всего и за счет влияния каждого фактора.
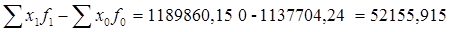 - абсолютное изменение объема продукции, - абсолютное изменение объема продукции,
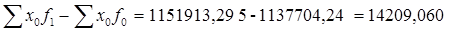 - абсолютное изменение численности рабочих, - абсолютное изменение численности рабочих,
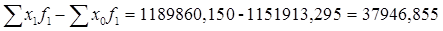 - абсолютное изменение производительности труда, - абсолютное изменение производительности труда,
Динамика средней выработки на одного рабочего по всей совокупности предприятий изучается на основе расчета следующих индексов:
1. Индекс переменного состава:
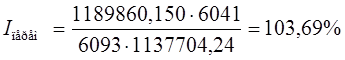
Он отражает изменение средней выработки в зависимости от влияния двух факторов: а) динамики производительности труда в каждой группе; б) структурных сдвигов в составе численности рабочих.
2. Индекс постоянного состава:
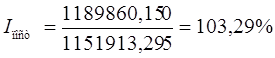
Он показывает как изменилась средняя выработка вследствие влияния только одного фактора — именно изменения выработки в каждой группе.
3. Индекс влияния структурных сдвигов:

Этот индекс отражает динамику средней выработки вследствие структурных сдвигов в численности рабочих. Связь между индексами следующая:
Реклама

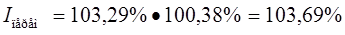
| Индекс объема продукции |
Абсолютное значение |
Индекс численности рабочих |
Абсолютное значение |
Индекс производительности |
Абсолютное значение |
| 104,58% |
52155,915 |
101,25% |
14209,060 |
103,29% |
37946,855 |
| Индекс переменного состава |
Индекс постоянного состава |
Индекс структурных сдвигов |
| 103,69% |
103,29% |
100,38% |
|