Задача 1. Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности
| Номер завода |
Среднегодовая стоимость ОПФ, млн.руб. |
Валовая продукция в сопоставимых ценах, млн. руб. |
| 1 |
3,4 |
3,5 |
| 2 |
3,1 |
3,3 |
| 3 |
3,5 |
3,5 |
| 4 |
4,1 |
4,5 |
| 5 |
5,8 |
7,5 |
| 6 |
5,2 |
6,9 |
| 7 |
3,8 |
4,3 |
| 8 |
4,1 |
5,9 |
| 9 |
5,6 |
4,8 |
| 10 |
4,5 |
5,8 |
| 11 |
4,2 |
4,5 |
| 12 |
6,1 |
8,4 |
| 13 |
6,5 |
7,3 |
| 14 |
2,0 |
2,1 |
| 15 |
6,4 |
7,8 |
| 16 |
4,0 |
4,2 |
| 17 |
8,0 |
10,6 |
| 18 |
5,1 |
5,8 |
| 19 |
4,9 |
5,3 |
| 20 |
4,3 |
4,9 |
| 21 |
5,8 |
6,0 |
| 22 |
7,2 |
10,4 |
| 23 |
6,6 |
6,9 |
| 24 |
3,0 |
3,5 |
| 25 |
6,7 |
7,2 |
С целью изучения зависимости между среднегодовой стоимостью ОПФ и выпуском валовой продукции производите группировку заводов по среднегодовой стоимости ОПФ, образовав 4 группы заводов с равными интервалами. По каждой группе и совокупности заводов подсчитайте:
1. число заводов;
2. среднегодовую стоимость ОПФ – всего и в среднем за один год;
3. стоимость валовой продукции - всего и в среднем за один год;
4. размер валовой продукции на один рубль ОПФ (фондоотдачу);
Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Решение
Величина интервала определяется по формуле:
i=R/m, где R- размах колебания признака;
R= xmax
– xmin
,
где xmax
,
xmin
соответственно максимальное и минимальное значение признака в совокупности;
m- число групп.
i = (xmax
– xmin
)/m = (8,0 – 2,0) / 4 = 6/4 = 1,5
| Группы заводов |
Число заводов |
Среднегодовая стоимость ОПФ, млн.руб. |
Стоимость валовой продукции, млн.руб. |
Фондоотдача (гр.6 / гр. 4) |
| Всего |
В среднем за год |
Всего |
В среднем за год |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 2 – 3,5 |
5 |
15 |
3 |
15,9 |
3,18 |
1,06 |
| 3,5 – 5,0 |
8 |
33,9 |
4,2375 |
39,4 |
4,925 |
1,162 |
| 5,0 – 6,5 |
8 |
46,5 |
5,8125 |
54,5 |
6,8125 |
1,172 |
| 6,5 – 8,0 |
4 |
28,5 |
7,125 |
35,1 |
8,775 |
1,232 |
Выводы:
Как видно по данным, представленным в таблице наиболее высокие показатели среднегодовой стоимости ОПФ, стоимости валовой продукции и фондоотдачи прослеживаются по 3 группе заводов и минимальные показатели по 1 группе.
Задача 2. Имеются следующие данные по зерновым культурам:
| Культура |
В отчетном периоде |
План на предстоящий период |
| Урожайность, ц/га |
Валовой сбор, ц |
Урожайность, ц/га |
Посевная площадь, га |
| Пшеница |
21,0 |
63 000 |
23,0 |
3 300 |
| Ячмень |
19,0 |
38 000 |
20,0 |
1 800 |
Вычислите среднюю урожайность зерновых культур:
1. в отчетном периоде;
2. в планируемом периоде.
Укажите, какой вид средней надо применить для вычисления этих показателей и какие изменения урожайности предусмотрены в плане на предыдущий период.
Решение
Для вычисления показателей применяем арифметическую среднюю взвешенную.
В отчетном периоде средняя урожайность зерновых культур составит:
х = (63 000 + 38 000)/ (63 000 : 21 + 38 000 : 19) = 101 000/(3 000 + 2000)=20,2 ц/га
В плановом периоде соответственно:
х = (23* 3 300 + 20 * 1 800)/ (3 300 + 1 800)= (75 900 + 36 000)/5 100 = 21,94 ц/га
В плане на предыдущий период намечается повышение средней урожайности зерновых культур на 1,74 ц/га (21,94 ц/га – 20,2 ц/га).
Задача 3. В целях изучения норм расходования сырья при изготовлении продукции на заводе проведена 10 % механическая выборка, в результате которой получено следующее распределение изделий по массе:
| Масса изделия, грамм |
Число изделий, шт. |
| До 20 |
10 |
| 20-21 |
20 |
| 21-22 |
50 |
| 22-23 |
15 |
| Свыше 23 |
5 |
| Итого |
100 |
На основе этих данных вычислите:
1. Среднюю массу изделия;
2. средний квадрат отклонений (дисперсию), среднее квадратическое отклонение;
Реклама

3. коэффициент вариации.
Решение
| Масса изделия, грамм (х) |
Число изделий, шт.(n) |
(х-хЇ) |
(х-хЇ)2
|
(х-хЇ)2
* n |
| 10 |
10 |
-9,6 |
92,16 |
921,6 |
| 20,5 |
20 |
0,9 |
0,81 |
16,2 |
| 21,5 |
50 |
1,9 |
3,61 |
180,5 |
| 22,5 |
15 |
2,9 |
8,41 |
126,15 |
| 23,5 |
5 |
3,9 |
15,21 |
76,05 |
| хЇ=19,6 |
100 |
1 320,5 |
Средняя масса изделий = (10*10+20,5*20+21,5*50+22,5*15+23,5*5)/100= 2 040/100 = 20,4 грамм;
Средний квадрат отклонений (дисперсия) = ∑((х-хЇ)2
* n)/∑n =1320,5/100 = 13,205;
Среднее квадратическое отклонение = √ (∑((х-хЇ)2
* n)/∑n) = √1320,5/100 = √13,205 = 3,6339
Коэффициент вариации = Среднее квадратическое отклонение/ хЇ*100 = 3,6339/19,6 * 100%= 0,1854 * 100 =18,54%.
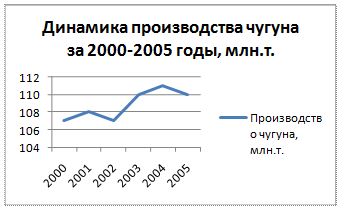
Задача 4. Производство чугуна на заводе характеризуется следующими показателями:
| Годы |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
| Производство чугуна,млн.т. |
107 |
108 |
107 |
110 |
111 |
110 |
Для анализа динамики производства вычислите:
1. Абсолютные приросты (или снижение), темпы роста и темпы прироста (или снижения) по годам и к 2000 году; абсолютное содержание 1 % прироста (снижения). Полученные данные представьте в таблице;
2. Среднегодовое производство чугуна;
3. среднегодовой темп роста и прироста производства чугуна.
Постройте график динамики производства чугуна за 2000-2005 гг. Сделайте выводы.
Решение
| Годы |
Производство чугуна,млн.т. |
Абсолютные приросты |
Темпы роста |
Темпы прироста |
Абсолютное содержание 1% прироста (гр.1/гр.7) |
| По годам |
К 2000 году |
По годам |
К 2000 году |
По годам |
К 2000 году |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 2000 |
107 |
- |
- |
100,0 |
100,0 |
- |
- |
- |
| 2001 |
108 |
1 |
1 |
100,93 |
100,93 |
0,9 |
0,93 |
1,1 |
| 2002 |
107 |
-1 |
0 |
99,0 |
100,0 |
-1,0 |
0,0 |
1,0 |
| 2003 |
110 |
3 |
3 |
102,8 |
102,8 |
2,8 |
2,8 |
1,07 |
| 2004 |
111 |
1 |
4 |
100,9 |
103,7 |
0,9 |
3,7 |
1,11 |
| 2005 |
110 |
-1 |
3 |
99,1 |
102,8 |
-0,9 |
2,8 |
1,11 |
Среднегодовое производство чугуна = (107+108+107+110+111+110)/6 = 653/6= 108,83 млн.т.
Среднегодовой темп роста = (100+100,93+99,0+102,8+100,9+99,1)/6= 602,73/6 = 100,455 %;
Среднегодовой темп прироста = 100,455 % - 100% = 0,455 %
Задача 5. Имеются следующие данные о товарных остатках в 3 квартале райпотребсоюза, млн. руб.
| Группа товаров |
На 1 июля |
На 1 августа |
На 1 сентября |
На 1 октября |
| Продовольственные товары |
1,5 |
1,4 |
1,5 |
1,8 |
| Непродовольственные товары |
3,5 |
3,8 |
3,7 |
3,4 |
Вычислите среднеквартальный остаток:
1. продовольственных товаров;
2. непродовольственных товаров;
3. по обеим товарным группам.
Поясните, почему методы расчета средних уровней рядов динамики в задачах 4 и 5 различны.
Решение
Среднеквартальный остаток составляет:
а) по продовольственным товарам = (1,5+1,4+1,5+1,8)/4 = 6,2/4 = 1,55 млн.р.
б) по непродовольственным товарам = (3,5+3,8+3,7+3,4)/4=14,4/4 = 3,6 млн.р.
в) по обеим товарным группам = (1,5 +3,5+1,4+3,8+1,5+3,7+1,8+3,4)/4=5,15 млн.р.
Для расчета среднеквартального остатка берутся остатки на каждое первое число месяца. Для расчета среднегодовых показателей принимаются для расчета только годовые суммы.
Задача 6. Динамика себестоимости и объема производства продукции характеризуется следующими данными:
| Вид продукции |
Выработано продукции, тыс.ед |
Себестоимость единицы продукции, руб. |
| Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
| Завод № 1 |
| МП-25 |
4,5 |
5,0 |
5,0 |
4,8 |
| ММ-29 |
3,2 |
3,0 |
8,0 |
8,2 |
| Завод № 2 |
| МП-25 |
10,6 |
10,0 |
7,0 |
6,6 |
На основании имеющихся данных вычислите:
1. Для завода № 1 (по двум видам продукции вместе):
а) общий индекс затрат на производство продукции;
б) общий индекс себестоимости продукции;
в) общий индекс физического объема производства продукции.
Определите в отчетном периоде изменение суммы затрат на производство продукции и разложите их по факторам (за счет изменения себестоимости и объема выработанной продукции).
Реклама

Покажите взаимосвязь между вычисленными индексами.
2. Для двух заводов вместе (по продукции МП-25):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости.
Объясните разницу между величинами индексов постоянного и переменного состава.
Решение
1. Общий индекс затрат (Izg
) = (∑ z1 *
g1
)/ (∑ z0 *
g0
) = (5*4,8+3*8,2)/(4,5*5+3,2*8) = 45/46,1=0,976 или 97,6 %;
Для определения влияния каждого из этих показателей в отдельности рассчитаем следующие показатели:
1) Индекс себестоимости (Iz
) = (∑ z1 *
g1
)/ (∑ z0 *
g1
) = (4,8*5+8,2*3)/(5*5+3*8) = 48,6/49 = 0,992 или 99,2 %
2) Индекс физического объема (Ig
) = (∑ z0 *
g1
)/ (∑ z0 *
g0
) = (5*5+8*3)/(5*4,5+8*3,2) = 49/48,1 = 1,019 или 101,9 %
3) Общий индекс затрат (Izg
) = (∑ z1 *
g1
)/ (∑ z0 *
g0
) = (4,8*5+8,2*3)/(5*4,5+8*3,2) = 48,6/48,1 =1,01 или 101 %
Или Izg
= Iz
*
Ig
=0,992 *1,019 =1,011 или 101%.
2. Индекс себестоимости переменного состава (Iпс
):
Iпс
= (∑ z1 *
d1
)/ (∑ z0 *
d0
) = (4.8*0.33 +6,6*0,66)/(5*0,298+7*0,702) = 5,94/6,404 = 0,928 или 92,8 % , где
d1
для завода № 1 = 5/(5+10) = 0,333 или 33,3 %;
d0
для завода № 1 = 4,5/ (4,5+10,6) = 0,298 или 29,8 %;
d1
для завода № 2 = 10/(5+10) = 0,666 или 66,6 %;
d0
для завода № 2 = 10,6/ (10,6+4,5) = 0,702 или 70,2 %.
Индекс фиксированного состава (Iфс
):
Iфс
= (∑ z1 *
d1
)/ (∑ z0 *
d1
) = (4,8*0,33+6,6*0,66)/(5*0,33+7*0,66) = 5,94/6,27 = 0,947 или 94,7 %;
Индекс структурных сдвигов (Iстр
) :
Iстр
= (∑ z0 *
d1
)/ (∑ z0 *
d0
)= (5*0,33+7*0,66)/(5*0,298 + 7*0,702) = 6,27/6,404 = 0,979 или 97,9 %
Проверка:
Iпс = Iфс
* Iстр
= 0,947 * 0979 = 0,928 или 92,8 %.
Разница между величинами индексов постоянного и переменного состава заключается в том, что при расчете индекса фиксированного состава количество выпускаемой продукции как в числителе так и в знаменателе берется на уровне отчетного периода, в то время как при расчете индекса переменного состава показатели одного отчетного периода сопоставляются с данными базисного периода.
Задача 7. Имеются следующие данные о товарообороте магазина потребительской кооперации:
| Товарная группа |
Продано товаров в фактических ценах, тыс.руб. |
| 3 квартал |
4 квартал |
| Мясо и мясопродукты |
36,8 |
50,4 |
| Молочные продукты |
61,2 |
53,6 |
В 4 квартале по сравнению с 3 кварталом цены на мясо и мясные продукты повысились в среднем на 5 %, а на молочные остались без изменения.
Вычислите:
1. Общий индекс товарооборота в фактических ценах.
2. Общий индекс цен.
3. Общий индекс физического объема товарооборота, используя взаимосвязь индексов.
Решение
Индекс товарооборота (Ipg
):
Ipg
= (∑g1
p1
)/(∑ g0
p0
) = (50.4*1.05+53.6*1.0)/(36.8*1+61.2*1) = 106.52/100 =1.065 или 106,5 %
Индекс цен (Ip
):
Ip
=(∑g1
p1
)/(∑ g1
p0
) = (1,05*50,4+1,0*53,6)/(1*50,4+1*53,6)=106,52/104 =1,024 или 102,4 %
Общий индекс физического объема товарооборота (Ig
):
Ig
= Ipg
/ Ip
= 1,065/1,024 =1,04
|