СОДЕРЖАНИЕ
С.
Введение 3
1 Теоретическая часть. Модели динамического программирования 4
1.1 Предмет динамического программирования 4
1.2 Постановка задачи динамического программирования 6
1.3 Принцип оптимальности и математическое описание динамического процесса управления 8 1.4Оптимальное распределение инвестиций 101.5 Выбор оптимальной стратегии обновления оборудования 13
2 Расчетная часть 16
Заключение 30
Список использованных источников 31
ВВЕДЕНИЕ
В настоящее время многие организации в своей деятельности сталкиваются с математическими моделями. Математическая модель – это система математических уравнений, неравенств, формул и различных математических выражений, описывающих поведение реального объекта, составляющих его характеристики взаимосвязи между ними. Процесс построения математической модели называется математическим моделированием. Моделирование и построение математической модели экономического объекта позволяют свести экономический анализ производственных процессов к математическому анализу и принятию эффективных решений. Для этого в планировании и управлении производством необходимо экономическую сущность исследуемого экономического объекта формализовать экономико-математической моделью, т. е. экономическую задачу представить математически.
Данная курсовая работа посвящена рассмотрению моделей динамического программирования. Динамическое программирование в широком смысле представляет собой оптимальное управление процессом, посредством изменения управляемых параметров на каждом шаге, и, следовательно, воздействуя на ход процесса, изменяя на каждом шаге состояние системы. Целью работы является рассмотрение примеров решения различных по своей природе задач, содержание которых требует выбора переменных состояния и управления. Особое внимание уделяется построению оптимальной последовательности операций в коммерческой деятельности.
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. МОДЕЛИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
1.1 ПРЕДМЕТ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Динамическое программирование представляет собой математический аппарат, который подходит к решению некоторого класса задач путем их разложения на части, небольшие и менее сложные задачи. При этом отличительной особенностью является решение задач по этапам, через фиксированные интервалы, промежутки времени, что и определило появление термина динамическое программирование. Следует заметить, что методы динамического программирования успешно применяются и при решении задач, в которых фактор времени не учитывается. В целом математический аппарат можно представить как пошаговое или поэтапное программирование. Решение задач методами динамического программирования проводится на основе сформулированного Р. Э. Беллманом принципа оптимальности: оптимальное поведение обладает тем свойством, что каким бы ни было первоначальное состояние системы и первоначальное решение, последующее решение должно определять оптимальное поведение относительно состояния, полученного в результате первоначального решения.Из этого следует, что планирование каждого шага должно проводиться с учетом общей выгоды, получаемой по завершении всего процесса, что и позволяет оптимизировать конечный результат по выбранному критерию.Таким образом, динамическое программирование в широком смысле представляет собой оптимальное управление процессом, посредством изменения управляемых параметров на каждом шаге, и, следовательно, воздействуя на ход процесса, изменяя на каждом шаге состояние системы.В целом динамическое программирование представляет собой стройную теорию для восприятия и достаточно простую для применения в коммерческой деятельности при решении как линейных, так и нелинейных задач.Динамическое программирование является одним из разделов оптимального программирования. Для него характерны специфические методы и приемы, применительные к операциям, в которых процесс принятия решения разбит на этапы (шаги). Методами динамического программирования решаются вариантные оптимизационные задачи с заданными критериями оптимальности, с определенными связями между переменными и целевой функцией, выраженными системой уравнений или неравенств. При этом, как и в задачах, решаемых методами линейного программирования, ограничения могут быть даны в виде равенств или неравенств. Однако если в задачах линейного программирования зависимости между критериальной функцией и переменными обязательно линейны, то в задачах динамического программирования эти зависимости могут иметь еще и нелинейный характер. Динамическое программирование можно использовать как для решения задач, связанных с динамикой процесса или системы, так и для статических задач, связанных, например, с распределением ресурсов. Это значительно расширяет область применения динамического программирования для решения задач управления. А возможность упрощения процесса решения, которая достигается за счет ограничения области и количества, исследуемых при переходе к очередному этапу вариантов, увеличивает достоинства этого комплекса методов.Вместе с тем динамическому программированию свойственны и недостатки. Прежде всего, в нем нет единого универсального метода решения. Практически каждая задача, решаемая этим методом, характеризуется своими особенностями и требует проведения поиска наиболее приемлемой совокупности методов для ее решения. Кроме того, большие объемы и трудоемкость решения многошаговых задач, имеющих множество состояний, приводят к необходимости отбора задач малой размерности либо использования сжатой информации. Последнее достигается с помощью методов анализа вариантов и переработки списка состояний.Для процессов с непрерывным временем динамическое программирование рассматривается как предельный вариант дискретной схемы решения. Получаемые при этом результаты практически совпадают с теми, которые получаются методами максимума Л. С. Понтрягина или Гамильтона-Якоби-Беллмана.Динамическое программирование применяется для решения задач, в которых поиск оптимума возможен при поэтапном подходе, например, распределение дефицитных капитальных вложений между новыми направлениями их использования; разработка правил управления спросом или запасами, устанавливающими момент пополнения запаса и размер пополняющего заказа; разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; составление календарных планов текущего и капитального ремонтов оборудования и его замены; поиск кратчайших расстояний на транспортной сети; формирование последовательности развития коммерческой операции и т. д. 1.2 ПОСТАНОВКА ЗАДАЧИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Постановку задачи динамического программирования рассмотрим на примере инвестирования, связанного с распределением средств между предприятиями. В результате управления инвестициями система последовательно переводится из начального состояния S0
в конечное Sn
. Предположим, что управление можно разбить на n шагов и решение принимается последовательно на каждом шаге, а управление представляет собой совокупность n пошаговых управлений. На каждом шаге необходимо определить два типа переменных: переменную состояния системы Sk
и переменную управления xk
. Переменная Sk
определяет, в каких состояниях может оказаться система на рассматриваемом k-м шаге. В зависимости от состояния S на этом шаге можно применить некоторые управления, которые характеризуются переменной xk
, которые удовлетворяют определенным ограничениям и называются допустимыми.Допустим, X = (x1
, x2
, …, xk
, …, xn
) – управление, переводящее систему из состояния S0
в состояние Sn
, a Sk
– есть состояние системы на k-м шаге управления. Тогда последовательность состояний системы можно представить в виде графа, изображенного на рис. 1.x1
x2
xk-1
xk
xk+1
xn
S0
→ S1
→ ... → Sk-1
→Sk
→ ... → Sn
Рисунок 1 – График состояний системыПрименение управляющего воздействия xk
на каждом шаге переводит систему в новое состояние S1
(S, xk
) и приносит некоторый результат Wk
(S, xk
). Для каждого возможного состояния на каждом шаге среди всех возможных управлений выбирается оптимальное управление х*k
, такое, чтобы результат, который достигается за шаги с k-го по последний n-й, оказался бы оптимальным. Числовая характеристика этого результата называется функцией Беллмана Fk
(S) и зависит от номера шага k и состояния системы S.
Задача динамического программирования формулируется следующим образом: требуется определить такое управление Х*, переводящее систему из начального состояния S0
в конечное состояние Sn
, при котором целевая функция принимает наибольшее (наименьшее) значение F(S0
, X*) → extr.Особенности математической модели динамического программирования заключаются в следующем:1) задача оптимизации формулируется как конечный многошаговый процесс управления;2) целевая функция (выигрыш) является аддитивной и равна сумме целевых функций каждого шага: F = ∑ Fk
(Sk
−1
, x k
) → extremum ;k =13) выбор управления хk
на каждом шаге зависит только от состояния системы к этому шагу Sk
−1
, и не влияет на предшествующие шаги (нет обратной связи);4) состояние системы Sk
после каждого шага управления зависит только от предшествующего состояния системы Sk
-1
и этого управляющего воздействия хk
(отсутствие последействия) и может быть записано в виде уравнения состояния: Sk
= fk
(Sk
-1, хk
), k = 1, n;5) на каждом шаге управление хk
зависит от конечного числа управляющих переменных, а состояние системы Sk
зависит от конечного числа параметров;6) оптимальное управление представляет собой вектор X*, определяемый последовательностью оптимальных пошаговых управлений: X = (х*1
, х*2
, …, х*k
, …, х*n
), число которых и определяет количество шагов задачи. 1.3 ПРИНЦИП ОПТИМАЛЬНОСТИ И МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИНАМИЧЕСКОГО ПРОЦЕССА УПРАВЛЕНИЯ
В основе метода динамического программирования лежит принцип оптимальности, впервые сформулированный в 1953 г. американским математиком Р. Э. Беллманом: каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая выигрыш на данном шаге. При решении задачи на каждом шаге выбирается управление, которое должно привести к оптимальному выигрышу. Если считать все шаги независимыми, тогда оптимальным управлением будет то управление, которое обеспечит максимальный выигрыш именно на данном шаге. Однако, например, при покупке новой техники взамен устаревшей на ее приобретение затрачиваются определенные средства, поэтому доход от ее эксплуатации в начале может быть небольшой, а в следующие годы новая техника будет приносить больший доход. И наоборот, если принято решение оставить старую технику для получения дохода в текущем году, то в дальнейшем это приведет к значительным убыткам. Этот пример демонстрирует следующий факт: в многошаговых процессах управление на каждом конкретном шаге надо выбирать с учетом его будущих воздействий на весь процесс.Кроме того, при выборе управления на данном шаге следует учитывать возможные варианты состояния предыдущего шага. Например, при определении количества средств, вкладываемых в предприятие в i-м году, необходимо знать, сколько средств осталось в наличии к этому году и какой доход получен в предыдущем (i-1)-м году. Таким образом, при выборе шагового управления необходимо учитывать следующие требования: 1) возможные исходы предыдущего шага Sk
-1
;2) влияние управления хk
на все оставшиеся до конца процесса шаги (n - k).В задачах динамического программирования первое требование учитывают, делая на каждом шаге условные предположения о возможных вариантах окончания предыдущего шага и проводя для каждого из вариантов условную оптимизацию. Выполнение второго требования обеспечивается тем, что в этих задачах условная оптимизация проводится от конца процесса к началу.Условная оптимизация.
На первом этапе решения задачи, называемом условной оптимизацией, определяются функция Беллмана и оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего в соответствии с алгоритмом обратной прогонки. На последнем, n-м шаге, оптимальное управление – х*n
определяется функцией Беллмана: F(S) = max {Wn
(S, xn
)}, в соответствии с которой максимум выбирается из всех возможных значений хn
, причем хn
∈Х.Дальнейшие вычисления производятся согласно рекуррентному соотношению, связывающему функцию Беллмана на каждом шаге с этой же функцией, но вычисленной на предыдущем шаге. В общем виде это уравнение имеет вид: Fn
(S) = max {Wn
(S, xn
) + Fk+1
(S1
(S, xk
))}, xk
∈Х.Этот максимум (или минимум) определяется по всем возможным для k и S значениям переменной управления X.Безусловная оптимизация.
После того, как функция Беллмана и соответствующие оптимальные управления найдены для всех шагов с n-го по первый, осуществляется второй этап решения задачи, называемый безусловной оптимизацией. Пользуясь тем, что на первом шаге (k = 1) состояние системы известно – это ее начальное состояние So
, можно найти оптимальный результат за все n шагов и оптимальное управление на первом шаге x1
, которое этот результат доставляет. После применения этого управления система перейдет в другое состояние S1
(S,х*1
), зная которое, можно, пользуясь результатами условной оптимизации, найти оптимальное управление на втором шаге х*2
, и так далее до последнего n-го шага. Вычислительную схему динамического программирования можно строить на сетевых моделях, а также по алгоритмам прямой прогонки (от начала) и обратной прогонки (от конца к началу). Рассмотрим примеры решения различных по своей природе задач, содержание которых требует выбора переменных состояния и управления.1.4 ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ИНВЕСТИЦИЙ
Требуется распределить имеющиеся В
единиц средств среди n предприятий, доход gi
(xi
) от которых, в зависимости от количества вложенных средств хi
, определяется матрицей (n*n), приведенной в табл. 1, так, чтобы суммарный доход со всех предприятий был бы максимальным. Таблица 1| x \ gi
|
g1
|
g2
|
… |
gi
|
… |
gn
|
| x1
|
g1
(x1
) |
g2
(x1
) |
… |
gi
(x1
) |
… |
gn
(x1
) |
| x2
|
g1
(x2
) |
g2
(x2
) |
… |
gi
(x2
) |
… |
gn
(x2
) |
| xi
|
… |
… |
… |
gi
(xi
) |
… |
… |
| xn
|
g1
(xn
) |
g2
(xn
) |
… |
… |
… |
gn
(xn
) |
Запишем математическую модель задачи.Определить  X* = (х*
1
, х*
2
, …, х*
i
, …, х*
n
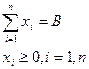), удовлетворяющий условиям и обеспечивающий максимум целевой функцииF(X) = ∑xi
gi
( xi
) → maxОчевидно, эта задача может быть решена простым перебором всех возможных вариантов распределения В единиц средств по n предприятиям, например на сетевой модели. Однако решим ее более эффективным методом, который заключается в замене сложной многовариантной задачи многократным решением простых задач с малым количеством исследуемых вариантов.С этой целью разобьем процесс оптимизации на n шагов и будем на каждом k-м шаге оптимизировать инвестирование не всех предприятий, а только предприятий с k-го по n-е. При этом естественно считать, что в остальные предприятия (с первого по (k–1)-е тоже вкладываются средства, и поэтому на инвестирование предприятий с k-го по n-е остаются не все средства, а некоторая меньшая сумма Сk
≤ В. Эта величина и будет являться переменной состояния системы. Переменной управления на k-м шаге назовем величину хk
средств, вкладываемых в k-e предприятие. В качестве функции Беллмана Fk
(Ck
) на k-м шаге можно выбрать максимально возможный доход, который можно получить с предприятий с k-го по n-е при условии, что на их инвестирование осталось Сk
средств. Очевидно, что при вложении в k-e предприятие хk
средств будет получена прибыль gk
(xk
), а система к (k+1)-му шагу перейдет в состояние Sk+1
и, следовательно, на инвестирование предприятий с (k+1)-го до n-го останется Сk+1
= (Сk
– хk
) средств.Таким образом, на первом шаге условной оптимизации при k = n функция Беллмана представляет собой прибыль только с n-го предприятия. При этом на его инвестирование может остаться количество средств Сn
, 0 ≤ Сn
≤ В. Чтобы получить максимум прибыли с этого предприятия, можно вложить в него все эти средства, т. е. Fn
(Сn
) = gn
(Сn
) и хn
= Сn
.На каждом последующем шаге для вычисления функции Беллмана необходимо использовать результаты предыдущего шага. Пусть на k-м шаге для инвестирования предприятий с k-го по n-е осталось Сk
средств (0 ≤ Сk
≤ В). Тогда от вложения в k-e предприятие хk
средств будет получена прибыль gk
(Ck
), а на инвестирование остальных предприятий (с k-го по n-е) останется Сk+1
= (Сk
– хk
) средств. Максимально возможный доход, который может быть получен с предприятий (с k-го по n-е), будет равен:Fk
(Ck
) = max {gk
(xk
) + Fk
+1
(сk
- xk
)} , k = 1, …, nМаксимум выражения достигается на некотором значении х*
k
, которое является оптимальным управлением на k-м шаге для состояния системы Sk
. Действуя таким образом, можно определить функции Беллмана и оптимальные управления до шага k = 1.Значение функции Беллмана F1
(c1
) представляет собой максимально возможный доход со всех предприятий, а значение х*
1
, на котором достигается максимум дохода, является оптимальным количеством средств, вложенных в первое предприятие. Далее на этапе безусловной оптимизации для всех последующих шагов вычисляется величина Сk
= (Сk-1
– хk-1
) оптимальным управлением на k-м шаге является то значение хk
, которое обеспечивает максимум дохода при соответствующем состоянии системы Sk
. 1.5 ВЫБОР ОПТИМАЛЬНОЙ СТРАТЕГИИ ОБНОВЛЕНИЯ ОБОРУДОВАНИЯ
Важной экономической проблемой является своевременное обновление оборудования: автомобилей, станков, телевизоров, магнитол и т. п. Старение оборудования включает физический и моральный износ, в результате чего растут затраты на ремонт и обслуживание, снижается производительность труда и ликвидная стоимость. Задача заключается в определении оптимальных сроков замены старого оборудования. Критерием оптимальности являются доход от эксплуатации оборудования (задача максимизации) либо суммарные затраты на эксплуатацию в течение планируемого периода (задача минимизации).Предположим, что планируется эксплуатация оборудования в течение некоторого периода времени продолжительностью n лет. Оборудование имеет тенденцию с течением времени стареть и приносить все меньший доход r(t) (t – возраст оборудования). При этом есть возможность в начале любого года продать устаревшее оборудование за цену S(t), которая также зависит от возраста t, и купить новое оборудование за цену P.Под возрастом оборудования понимается период эксплуатации оборудования после последней замены, определенный в годах. Требуется найти оптимальный план замены оборудования с тем, чтобы суммарный доход за все n лет был бы максимальным, учитывая, что к началу эксплуатации возраст оборудования составлял t0
лет.Исходными данными в задаче являются доход r(t) от эксплуатации в течение одного года оборудования возраста t лет, остаточная стоимость S(t), цена нового оборудования P и начальный возраст оборудования t0
.Таблица 2| t |
0 |
1 |
… |
n |
| r |
r(0) |
r(1) |
… |
r(n) |
| S |
S(0) |
S(1) |
… |
S(n) |
При составлении динамической модели выбора оптимальной стратегии обновления оборудования процесс замены рассматривается как n-шаговый, т. е. период эксплуатации разбивается на n-шагов.Выберем в качестве шага оптимизацию плана замены оборудования с k-го по n-й годы. Очевидно, что доход от эксплуатации оборудования за эти годы будет зависеть от возраста оборудования к началу рассматриваемого шага, т. е. k-го года.Поскольку процесс оптимизации ведется с последнего шага (k = n), то на k-м шаге неизвестно, в какие годы с первого по (k-1)-й должна осуществляться замена и, соответственно, неизвестен возраст оборудования к началу k-го года. Возраст оборудования, который определяет состояние системы, обозначим t. На величину t накладывается следующее ограничение:1 ≤ t ≤ t0
+ k – 1Это выражение свидетельствует о том, что t не может превышать возраст оборудования за (k–1)-й год его эксплуатации с учетом возраста к началу первого года, который составляет t0
лет; и не может быть меньше единицы (этот возраст оборудование будет иметь к началу k-го года, если замена его произошла в начале предыдущего (k–1)-го года).Таким образом, переменная t в данной задаче является переменной состояния системы на k-м шаге. Переменной управления на k-м шаге является логическая переменная, которая может принимать одно из двух значений: сохранить (С) или заменить (З) оборудование в начале k-го года: xk
(t) = { С, если оборудование сохраняется { З, если оборудование заменяетсяФункцию Беллмана Fk
(t) определяют как максимально возможный доход от эксплуатации оборудования за годы с k-го по n-й, если к началу k-го возраст оборудования составлял t лет. Применяя то или иное управление, система переходит в новое состояние. Так, например, если в начале k-го года оборудование сохраняется, то к началу (k + 1)-го года его возраст увеличится на единицу (состояние системы станет t+1), в случае замены старого оборудования новое достигнет к началу (k + 1)-го года возраста t = 1 год.На этой основе можно записать уравнение, которое позволяет рекуррентно вычислить функции Беллмана, опираясь на результаты предыдущего шага. Для каждого варианта управления доход определяется как сумма двух слагаемых: непосредственного результата управления и его последствий.Если в начале каждого года сохраняется оборудование, возраст которого t лет, то доход за этот год составит r(t). К началу (k+1)-го года возраст оборудования достигнет (t+1) и максимально возможный доход за оставшиеся годы (с (k+1)-го по n-й) составит Fk+1
(t+1). Если в начале k-го года принято решение о замене оборудования, то продается старое оборудование возраста t лет по цене S(t), приобретается новое за P единиц, а эксплуатация его в течение k-го года нового оборудования принесет прибыль r(0). К началу следующего года возраст оборудования составит 1 год и за все оставшиеся годы с (k+1)-го по n-й максимально возможный доход будет Fk+1
(1). Из двух возможных вариантов управления выбирается тот, который приносит максимальный доход. Функция Fk
(t) вычисляется на каждом шаге управления для всех 1 ≤ t ≤ t0
+ k – 1. Управление при котором достигается максимум дохода, является оптимальным.Значения функции Fn
(t), определяемые Fn-1
(t), Fn-2
(t) вплоть до F1
(t). F1
(t0
) представляют собой возможные доходы за все годы. Максимум дохода достигается при некотором управлении, применяя которое на первом году, мы определяем возраст оборудования к началу второго года. Для данного возраста оборудования выбирается управление, при котором достигается максимум дохода за годы со второго по n-й и так далее. В результате на этапе безусловной оптимизации определяются годы, в начале которых следует произвести замену оборудования.2 РАСЧЕТНАЯ ЧАСТЬ
Построение оптимальной последовательности операций в коммерческой деятельности
Пример
Пусть на оптовую базу «Ларес» прибыло 10 машин с товаром для разгрузки и 8 машин для загрузки товаров, направляемых в магазины. Материально-ответственное лицо оптовой базы осуществляет оформление документов по операциям разгрузки или загрузки для одной машины, а затем переходит к обслуживанию другой машины. Известны затраты по выполнению каждой операции, которые показаны на ребрах графа (рис. 2).Издержки от операций обусловлены простоем транспорта, типом операции (прием или отправка товара) и не зависят от конкретной машины. Необходимо спланировать последовательность операций обоих видов таким образом, чтобы суммарные издержки по приему и отправке товаров для всех машин были минимальными.Решение:
Из условия следует, что состояние экономической системы характеризуется двумя параметрами: количеством принятых и оформленных машин по разгрузке товара и количеством машин, отправленных с товаром в магазины. Поэтому решение будем искать на плоскости X0Y, на ограниченном прямыми прямоугольнике, который является областью допустимых состояний системы. Если по оси X отложить число (10) разгруженных машин, а по оси Y – число (8) загруженных товаром машин, то можно построить на плоскости граф состояний процесса, в котором каждая вершина характеризует состояние операции приема и отгрузки товара на оптовой базе. Ребра этого графа означают выполнение работы по приему или отправке товара на очередной машине. Каждому ребру можно сопоставить издержки, связанные с выполнением операции по разгрузке или загрузке машины.Точка S0
определяет начало процесса, a S1
– конечное состояние, соответствующее приему и отправке всех машин. Оптимизацию процесса будем производить с конечного состояния S1
. Весь процесс разобьем на шаги, их количество k = n + m = 10 + 8 = 18. Каждый шаг представляет собой сечение графа состояний, проходящее через вершины (на рис. 2 сечения показаны косыми линиями).
  К=18 К=17 К=16 К=15 К=14 К=13 К=12 К=11 К=10 К=9Рисунок 2 – Графическая схема связи операцийI этап. Условная оптимизация.
1-й шаг. k = 1. На первом шаге, с задаваемым сечением А1
В1
, из состояний А1
и B1
возможен только один вариант перехода в конечное состояние S1
. Поэтому в вершинах А1
и B1
записываем соответственно издержки 13 и 10. Ребра A1
S1
и B1
Sl
обозначаем стрелкой, направленной в вершину S1
, как показано на рис. 3.   Рисунок 3 – Сетевая модель операции, шаг 1 2-й шаг. k = 2. Второй шаг оптимизации задается сечением по вершинам А2
, В2
, C1
. Из состояний А2
и C1
возможен единственный переход в вершины А1
и B1
соответственно, поэтому в вершинах А2
и C1
записываем суммарные издержки 29 и 28 на первых двух шагах перехода в конечное состояние S1
. Из вершины В2
возможны два варианта перехода: в вершину А1
или вершину B1
. При переходе В2
→ А1
сумма издержек составляет 11 + 13 = 24, на переходе В2
→ В1
сумма составляет 15 + 10 = 25. Из двух вариантов суммарных издержек выбираем наименьшую (24) и обозначаем стрелкой условно оптимальный переход В2
→ А1
, как показано на рис. 4.
Рисунок 4 – Сетевая модель операции, шаг 2 3-й шаг. k = 3. На третьем шаге сечение проходит через вершины А3
, В3
, С2
, D1
. Из вершин А3
и D1
возможен единственный переход в вершины А2
и С1
соответственно. Суммарные издержки для состояния D1
равны 28 + 19 = 47; для состояния А3
: 29 + 20 = 49. Из вершины В3
возможны два варианта перехода: в вершину А2
издержки равны 29 + 9 = 38; в вершину В2
– 13 + 24 = 37
. Для вершины С2
возможен переход в вершину В2
(21 + 24 = 45)
и в вершину С1
(18 + 28 = 46). Выбираем для вершин В3
и С2
наименьшие суммарные издержки и обозначаем стрелкой условно оптимальный переход, как показано на рис. 5.
Рисунок 5 – Сетевая модель операции, шаг 3 4-й шаг. k = 4. Четвертый шаг оптимизации задается сечением по вершинам А4
, В4
, C3
, D2
, Е1
. Из состояний А4
и Е1
возможен единственный переход в вершины А3
и D1
соответственно, поэтому в вершинах А4
и Е1
записываем суммарные издержки:А4
А3
: 18 + 49 = 67
Е1
D1
: 18 + 47 = 65.
Вершина В4
: В4
А3
: 10 + 49 =59 В4
В3
: 13 + 37 = 50.
Вершина С3
: С3
В3
: 20 + 37 =57
С3
С2
: 21 + 45 = 66.Вершина D2
: D2
С2
: 19 + 45 =64 D2
D1
: 11 + 47 = 58.
Рисунок 6 – Сетевая модель операции, шаг 4 5-й шаг. k = 5. На пятом шаге сечение проходит через вершины А5
, В5
, С4
, D3
, Е2
, F1
. Из вершин А5
и F1
возможен единственный переход в вершины А4
и Е1
соответственно:А5
А4
: 15 + 67 = 82
F
1
Е1
: 16 + 65 = 81.
Вершина В5
: В5
А4
: 13 + 67 =80 В5
В4
: 12 + 50 = 62.
Вершина С4
: С4
В4
: 18 + 50 = 68
С4
С3
: 12 + 57 = 69.Вершина D3
: D3
С3
: 18 + 57 = 75 D3
D2
: 11 + 58 = 69.
Вершина Е2
: Е2
D2
: 16 + 58 = 74
Е2
Е1
: 15 + 65 = 80.
Рисунок 7 – Сетевая модель операции, шаг 5 6-й шаг. k = 6. Шестой шаг оптимизации задается сечением по вершинам А6
, В6
, C5
, D4
, Е3
, F2
, G1
. Из состояний А6
и G1
возможен единственный переход в вершины А5
и F1
соответственно, поэтому в вершинах А6
и G1
записываем суммарные издержки:А6
А5
: 13 + 82 = 95
G
1
F
1
: 10 + 81 = 91.
Вершина В6
: В6
А5
: 14 + 82 =96 В
6
В
5
: 1
5
+
62
=
77
.
Вершина С5
: С5
В5
: 10 + 62 = 72
С5
С4
: 12 + 68 = 80.Вершина D4
: D4
С4
: 16 + 68 = 84 D4
D3
: 12 + 69 = 81.
Вершина Е3
: Е
3
D
3
: 1
5
+
69
=
8
4
Е3
Е2
: 14 + 74 = 88.Вершина F2
: F
2
Е
2
: 1
5
+
74
=
89
F2
F1
: 12 + 81 = 93.
Рисунок 8 – Сетевая модель операции, шаг 6 7-й шаг. k = 7. Сечение А7
, В7
, C6
, D5
, Е4
, F3
, G2
, Н1
. Вершина А7
: А7
А6
: 18 + 95 = 113
Вершина Н1
: Н1
G
1
: 11 + 91 = 102
Вершина В7
: В7
А6
: 15 + 95 = 110 В7
В6
: 18 + 77 = 95.
Вершина С6
: С6
В6
: 9 + 77 = 86 С6
С5
: 13 + 72 = 85.
Вершина D5
: D5
С5
: 15 + 72 = 87
D5
D4
: 10 + 81 = 91.Вершина Е4
: Е4
D4
: 15 + 81 = 96
Е4
Е3
: 14 + 84 = 98.Вершина F3
: F3
Е3
: 16 + 84 = 100F
3
F
2
: 10 +
8
9 =
9
9.
Вершина G2
: G2
F2
: 14 + 89 = 103G
2
G
1
: 11 + 91 = 102.
8-й шаг. k = 8. Сечение А8
, В8
, C7
, D6
, Е5
, F4
, G3
, Н2
, I1
. Вершина А8
: А8
А7
: 16 + 113 = 129
Вершина I1
: I
1
Н1
: 12 + 102 = 114
Вершина В8
: В8
А7
: 14 + 113 = 127 В8
В7
: 20 + 95 = 115.
Вершина С7
: С7
В7
: 15 + 95 = 110 С7
С6
: 11 + 85 = 96.
Вершина D6
: D6
С6
: 13 + 85 = 98
D6
D5
: 13 + 87 = 100.Вершина Е5
: Е5
D5
: 13 + 87 = 100
Е5
Е4
: 10 + 96 = 106.Вершина F4
: F
4
Е4
: 14 + 96 = 110
F4
F3
: 18 + 99 = 117.Вершина G3
: G
3
F
3
: 12 + 99 = 111
G3
G2
: 18 + 102 = 120.Вершина Н2
: Н2
G2
: 17 + 102 = 119Н2
Н1
: 12 + 102 = 114.
9-й шаг. k = 9. Сечение А9
, В9
, C8
, D7
, Е6
, F5
, G4
, Н3
, I2
. Вершина А9
: А9
А8
: 10 + 129 = 139
Вершина В9
: В9
А8
: 13 + 129 = 142 В9
В8
: 10 + 115 = 125.
Вершина С8
: С8
В8
: 16 + 115 = 131 С8
С7
: 9 + 96 = 105.
Вершина D7
: D7
С7
: 14 + 96 = 110
D7
D6
: 14 + 98 = 112.Вершина Е6
: Е6
D6
: 15 + 98 = 113
Е6
Е5
: 15 + 100 = 115.Вершина F5
: F
5
Е5
: 12 + 100 = 112
F5
F4
: 16 + 110 = 126.Вершина G4
: G4
F4
: 19 + 110 = 129G
4
G
3
: 9 + 111 = 120.
Вершина Н3
: Н3
G3
: 16 + 111 = 127Н3
Н2
: 10 + 114 = 124.
Вершина I2
: I2
Н2
: 11 + 114 = 125I
2
I
1
: 8 + 114 = 122.
10-й шаг. k = 10. Сечение А10
, В10
, C9
, D8
, Е7
, F6
, G5
, Н4
, I3
. Вершина А10
: А10
А9
: 14 + 139 = 153
Вершина В10
: В10
А9
: 12 + 139 = 151 В10
В9
: 10 + 125 = 135.
Вершина С9
: С9
В9
: 15 + 125 = 140 С9
С8
: 18 + 105 = 123.
Вершина D8
: D8
С8
: 13 + 105 = 118
D8
D7
: 15 + 110 = 125.Вершина Е7
: Е7
D7
: 14 + 110 = 124
Е7
Е6
: 13 + 113 = 126.Вершина F6
: F
6
Е6
: 12 + 113 = 125
F6
F5
: 19 + 112 = 131.Вершина G5
: G
5
F
5
: 13 + 112 = 125
G5
G4
: 11 + 120 = 131.Вершина Н4
: Н4
G
4
: 16 + 120 = 136
Н4
Н3
: 15 + 124 = 139.Вершина I3
: I
3
Н3
: 11 + 124 = 135
I3
I2
: 15 + 122 = 137. 11-й шаг. k = 11. Сечение В11
, C10
, D9
, Е8
, F7
, G6
, Н5
, I4
. Вершина В11
: В11
А10
: 10 + 153 = 163 В11
В10
: 9 + 135 = 144.
Вершина С10
: С10
В10
: 10 + 135 = 145 С10
С9
: 10 + 123 = 133.
Вершина D9
: D9
С9
: 13 + 123 = 136 D9
D8
: 14 + 118 = 132.
Вершина Е8
: Е8
D8
: 11 + 118 = 129
Е8
Е7
: 14 + 124 = 138.Вершина F7
: F
7
Е7
: 10 + 124 = 134
F7
F6
: 18 + 125 = 143.Вершина G6
: G
6
F
6
: 11 + 125 = 136
G6
G5
: 18 + 125 = 143.Вершина Н5
: Н5
G
5
: 15 + 125 = 140
Н5
Н4
: 19 + 136 = 155.Вершина I4
: I4
Н4
: 16 + 136 = 152I
4
I
3
: 14 + 135 = 149.
12-й шаг. k = 12. Сечение C11
, D10
, Е9
, F8
, G7
, Н6
, I5
. Вершина С11
: С11
В11
: 11 + 144 = 155 С11
С10
: 8 + 133 = 141.
Вершина D10
: D10
С10
: 15 + 133 = 148 D10
D9
: 13 + 132 = 145.
Вершина Е9
: Е9
D9
: 15 + 132 = 147 Е9
Е8
: 14 + 124 = 138.
Вершина F8
: F
8
Е8
: 9 + 129 = 141
F8
F7
: 21 + 134 = 155.Вершина G7
: G
7
F
7
: 12 + 134 = 146
G7
G6
: 13 + 136 = 149.Вершина Н6
: Н6
G
6
: 15 + 136 = 151
Н6
Н5
: 16 + 140 = 156.Вершина I5
: I
5
Н5
: 11 + 140 = 151
I5
I4
: 9 + 149 = 158. 13-й шаг. k = 13. Сечение D11
, Е10
, F9
, G8
, Н7
, I6
. Вершина D11
: D11
С11
: 11 + 141 = 152
D11
D10
: 12 + 145 = 157.Вершина Е10
: Е10
D10
: 16 + 145 = 161 Е10
Е9
: 13 + 141 = 154.
Вершина F9
: F
9
Е9
: 11 + 141 = 152
F9
F8
: 20 + 138 = 158.Вершина G8
: G
8
F
8
: 14 + 138 = 152
G8
G7
: 12 + 146 = 158.Вершина Н7
: Н7
G
7
: 14 + 146 = 160
Н7
Н6
: 13 + 151 = 164.Вершина I6
: I
6
Н6
: 10 + 151 = 161
I6
I5
: 17 + 151 = 168. 14-й шаг. k = 14. Сечение Е11
, F10
, G9
, Н8
, I7
. Вершина Е11
: Е11
D11
: 9 + 152 = 161
Е11
Е10
: 11 + 154 = 165.Вершина F10
: F
10
Е10
: 15 + 154 = 169
F10
F9
: 19 + 152 = 171.Вершина G9
: G9
F9
: 13 + 152 = 165G
9
G
8
: 12 + 152 = 164.
Вершина Н8
: Н8
G
8
: 13 + 152 = 165
Н8
Н7
: 15 + 160 = 175.Вершина I7
: I
7
Н7
: 9 + 160 = 169
I7
I6
: 16 + 161 = 177. 15-й шаг. k = 15. Сечение F11
, G10
, Н9
, I8
. Вершина F11
: F
11
Е11
: 16 + 161 = 177
F11
F10
: 18 + 169 = 187.Вершина G10
: G10
F10
: 10 + 169 = 179G
10
G
9
: 10 + 164 = 174.
Вершина Н9
: Н9
G
9
: 9 + 164 = 173
Н9
Н8
: 12 + 165 = 177.Вершина I8
: I
8
Н8
: 13 + 165 = 178
I8
I7
: 14 + 169 = 183. 16-й шаг. k = 16. Сечение G11
, Н10
, I9
. Вершина G11
: G11
F11
: 9 + 177 = 186G
11
G
10
: 10 + 174 = 184.
Вершина Н10
: Н10
G10
: 10 + 174 = 184Н10
Н9
: 10 + 173 = 183.
Вершина I9
: I
9
Н9
: 11 + 173 = 184
I9
I8
: 10 + 178 = 188. 17-й шаг. k = 17. Сечение Н11
, I10
. Вершина Н11
: Н11
G11
: 10 + 184 = 194Н11
Н10
: 9 + 183 = 192.
Вершина I10
: I
10
Н10
: 9 + 183 = 192
I10
I9
: 15 + 184 = 199. 18-й шаг. k = 18. Вершина S0
: S0
Н11
: 10 + 192 = 202
S0
I10
: 13 + 192 = 205. Минимально возможные суммарные издержки по обслуживанию всех 18 машин на оптовой базе «Ларес» составляют 202 усл. ед.II этап. Безусловная оптимизация.
Определяем оптимальную траекторию на исходном сетевом графе, просматривая результаты всех шагов в обратном порядке, учитывая, что выбор некоторого управления на k-м шаге приводит к тому, что состояние на (k-1)-м шаге становится определенным. В результате строим ориентированный граф от состояния S0
к состоянию S1
, представленный на рис. 9, на каждом шаге безусловной оптимизации переход почти всегда единствен и совпадает с построенными условно оптимальными переходами.
Рисунок 9 – Оптимальная последовательность операцийМинимальные издержки Fmin
соответствуют следующему оптимальному пути на графе:(S0
→ H11
→ H10
→ H9
→ G9
→ G8
→ F8
→ E8
→ D8
→ C8
→ C7
→ C6
→ → C5
→ B5
→ B4
→ B3
→ B2
→ A1
→ S1
) иравны: Fmin
= 10 + 9 + 10 + 9 + 12 + 14 + 9 + 11 + 13 + 9 + 11 + 13 + 10 + 12 + 13 + + 13 + 11 + 13 = 202 усл. ед. Таким образом, в соответствии с решением оптимальное управление процессом разгрузки и загрузки машин товаром состоит в следующем: на первом шаге следует оформить документы по загрузке одной машины, на втором – по разгрузке двух машин, затем по загрузке одной машины; далее обслуживать одну машину по разгрузке товара, четыре машины по загрузке, три машины по разгрузке, одну машину по загрузке; в последнюю очередь оформить документы по разгрузке трех машин, по загрузке одной машины и разгрузить последнюю машину.ЗАКЛЮЧЕНИЕ
Динамическое программирование связано с возможностью представления процесса управления в виде цепочки последовательных действий, или шагов, развернутых во времени и ведущих к цели. Таким образом, процесс управления можно разделить на части и представить его в виде динамической последовательности и интерпретировать в виде пошаговой программы, развернутой во времени. Это позволяет спланировать программу будущих действий. Поскольку вариантов возможных планов–программ множество, то необходимо из них выбрать лучший, оптимальный по какому-либо критерию в соответствии с поставленной целью.В курсовой работе основное внимание уделено подробному рассмотрению задачипостроения оптимальной последовательности операций в коммерческой деятельности. Динамическое программирование также применяется для решения таких задач, как распределение дефицитных капитальных вложений между новыми направлениями их использования; разработка правил управления спросом или запасами, устанавливающими момент пополнения запаса и размер пополняющего заказа; разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; составление календарных планов текущего и капитального ремонтов оборудования и его замены; поиск кратчайших расстояний на транспортной сети и т. д.В заключение можно отметить, что методы динамического программирования успешно применяются и при решении задач, в которых фактор времени не учитывается.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1 Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. – М.: Финансы и статистика, 2001.- 544 с.
2 Ломкова Е. Н., Эпов А. А. Экономико-математические модели управления производством (теоретические аспекты): Учеб. пособие. – Волгоград: ВолгГТУ, 2005. – 67 с.3 Холод Н. И., Кузнецов А. В., Жихар Я. Н. и др.; под общ. ред. Кузнецова А. В. Экономико-математические методы и модели: Учеб. пособие. –Мн.: БГЭУ, 2000. – 412 с.4 Шикин Е. В., Чхартищвили А. Г. Математические методы и модели в управлении: Учеб. пособие. – 2-е издание, испр. – М.: Дело, 2002. – 440 с. |
