Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
«Финансовый университет при Правительстве Российской Федерации»
Кафедра «Математическое моделирование экономических процессов»
ТЕОРЕТИКО-ПРАКТИЧЕСКАЯ РАБОТА
по эконометрике
Выполнил:
студент группы РЦБ 3-2 Власов Кирилл
______________________.
Научный руководитель:
к.т.н., профессор Невежин В.П
______________________.
Дата:
« ___ » ____________ 2010 г.
Москва 2010
Оглавление
I.Введение – задание. 3
II.Формулы расчетов. 3
III.Исходные данные. 3
IV.Модели. 3
1.Линейная модель. 3
a)ОАО «РусГидро» (полный анализ). 3
b)ОАО «ЛУКОЙЛ» (результаты исследования). 3
c)ОАО «Сбербанк» (результаты исследования). 3
d)ОАО «Татнефть» (результаты исследования). 3
e)ОАО «Газпром» (результаты исследования). 3
2.Степенная модель. 3
a)ОАО «ЛУКОЙЛ» (полный анализ). 3
b)ОАО «РусГидро» (результаты исследования). 3
c)ОАО «Сбербанк» (результаты исследования). 3
d)ОАО «Татнефть» (результаты исследования). 3
e)ОАО «Газпром» (результаты исследования). 3
3.Показательная модель. 3
a)ОАО «Сбербанк России» (полный анализ). 3
b)ОАО «РусГидро» (результаты исследования). 3
c)ОАО «ЛУКОЙЛ» (результаты исследования). 3
d)ОАО «Татнефть» (результаты исследования). 3
e)ОАО «Газпром» (результаты исследования). 3
4.Модель равносторонняя гипербола. 3
a)ОАО «Татнефть» (Полный анализ). 3
b)ОАО «РусГидро» (результаты исследования). 3
c)ОАО «ЛУКОЙЛ» (результаты исследования). 3
d)ОАО «Сбербанк» (результаты исследования). 3
e)ОАО «Газпром» (результаты исследования). 3
V.Портфель. 3
VI.Прогноз. 3
VII.Выводы:3
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ... 3
Одним из основных механизмов для привлечения и перераспределения капиталов является фондовый рынок, где происходит купля-продажа ценных бумаг.
За последние десятилетия в структуре мирового фондового рынка произошли большие изменения. Неизмеримо увеличились разнообразие его инструментов и усложнилась институциональная структура.
Закончилась эпоха абсолютного господства на мировых фондовых рынках десятка ведущих промышленно развитых стран. Начиная с 1980 года неуклонно возрастает удельный вес формирующихся, развивающихся фондовых рынков, к которым относится и Российский фондовый рынок.
Реклама

Отечественный рынок ценных бумаг, характеризующийся интенсивным ростом количества находящихся в обращении ценных бумаг и объемов торгов, стал важной и неотъемлемой частью экономической жизни нашей страны, что обусловило включение России в систему мирового финансового рынка, присвоение стране международных кредитных рейтингов.
В своей практической деятельности современный трейдер не может обойтись без применения математических методов. Эконометрический анализ позволяет ему определить объекты для инвестирования с целью максимизации доходности своих средств.
Данная работа посвящена исследованию выбора модели, которая лучше всего бы описывала колебания цен акций в зависимости от индекса РТС, и алгоритма построения оптимального портфеля этих ценных бумаг.
В качестве них выбраны котирующиеся на бирже РТС акции пяти крупных эмитентов: ОАО «РусГидро», ОАО «ЛУКОЙЛ», ОАО «Сбербанк», ОАО «Татнефть» и ОАО «Газпром». Исходные данные взяты с сайта РТС в разделе календаря с итогами торгов за каждый день. Для анализа были выбраны данные по средневзвешенным ценам вышеперечисленных акций за май – июнь 2010 года.
По полученным данным был проведен полный эконометрический анализ модели зависимости цены каждой бумаги от цены на индекс РТС, основанной на следующих функциях:
- линейная
- степенная
- показательная
- равносторонняя гипербола
Для каждой указанной функции была:
А) проведена оценка параметров уравнения парной регрессии;
Б) определена теснота связи с помощью показателей корреляции и детерминации;
В) была дана с помощью среднего коэффициента эластичности сравнительная оценка силы связи фактора с результатом.
Г) оценены полученные данные с использованием средней ошибки аппроксимации и F–критерия Фишера.
Д) проведена оценка каждой из полученных моделей из уравнений парной регрессии:
- используя F – тест;
- используя интервальное прогнозирование проверена адекватность оцененной модели
- рассчитаны прогнозные значения цены каждой акции на предполагаемую дату продажи акций, например, 10 дней, 20 дней, 30 дней. Доверительный интервал прогноза для уровня значимости ά = 0,05
Результаты каждого исследования оформляются в таблицу:
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
0 |
Yt
= а0
+ а1
*Xt
|
Та
= |
0 |
| а1
= |
0 |
Тв
= |
0 |
| Дисперсии Х и У
|
средние квадрат. отклонения
|
Tr
= |
0 |
| S2
х= |
0 |
Sx= |
0 |
Tkp
= |
0 |
| S2
у= |
0 |
Sy= |
0 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0 |
R2= |
0 |
| Проверка значимости уравнения регрессии
|
GQ= |
0 |
GQ-1
= |
0 |
| DW= |
0 |
dl= |
0 |
Du= |
0 |
| Dфакт= |
0 |
Dост= |
0 |
F= |
0 |
Fкр
= |
0 |
Вторая часть работы включает составление оптимального портфеля из соответствующих акций.
Для линейной парной регрессионной модели необходимо рассчитать прогноз дисперсии цены каждой бумаги и индекс РТС на выбранную дату. Для этих целей следует сформировать вектор цен на выбранную дату:
Реклама

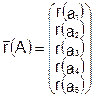
и вычислить ковариационную матрицу, элементы которой определяются исходя из полученных моделей:
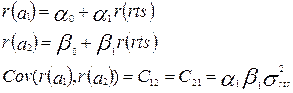
По аналогии следует вычислить остальные компоненты ковариационной матрицы и представить ее в следующем виде:
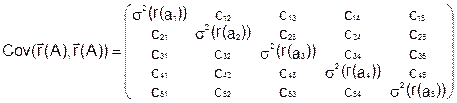
В результате должна быть получена необходимая информация для формирования модели Марковца: 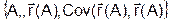
ЗАМЕЧАНИЕ.
Марковец предлагает интерпретировать элементы вектора r как меру привлекательности бумаги, а соответствующую ей дисперсию как меру риска вложений в бумагу.
Теперь можно приступить к формированию оптимального портфеля выбранных бумаг.
1. Портфель Р состоит из количеств акций каждого типа:
Р={n1
, n2
, n3
, n4
, n5
}.
2. Для удобства в соответствие портфелю Р можно поставить вектор X={x1
, x2
, x3
, x4
, x5
}, где xi
– доля бумаг типа i в портфеле. При этом:
x1
+ x2
+ x3
+ x4
+ x5
=1
3. Обозначим символом rp
выручку портфеля в целом за период владения. Эта выручка может быть рассчитана как:
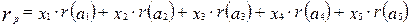 (1) (1)
где
xi
– доля бумаги типа i в пакете
r(ai
) – цена i-ой бумаги на выбранную дату
Так как выручка портфеля величина случайная, следовательно, для нее можно рассчитать математическое ожидание и дисперсию.
Математическое ожидание будет вычисляться по формуле (1), т.к. прогнозные значения r(ai
) вычислены по регрессионной модели.
Дисперсия портфеля, в целом, будет определяться по формуле 2, т.е.:
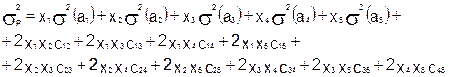 (2) (2)
Доходность и дисперсия портфеля являются его составными функциями.
3.2. Найти портфель, соответствующий минимальному риску. Для этого следует решить следующую задачу математического программирования:
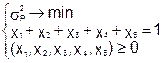 (3) (3)
Решение задачи (3) позволит получить значение минимального риска σР
и соответствующий ему портфель из выбранных бумаг.
Пусть σ0
> σР
некоторое значение риска. Тогда портфель называется оптимальным, если его доходность максимальна при заданном значении риска σ0
.
Оптимальный портфель – это решение задачи математического программирования:
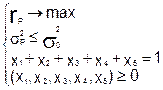 (4) (4)
3.3. Задав три значения для σ0
, следует получить три соответствующих оптимальных портфеля из выбранных бумаг, а затем определить из них наилучший.
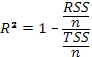
1.
ЛИНЕЙН
1.1. 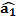 – оценки коэффициентов регрессии, – оценки коэффициентов регрессии,
| ЛИНЕЙН()
|
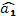 |
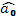 |
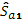 |
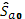 |
| R^2 |
Sε |
| F |
f2 |
| RSS |
ESS |
1.2. 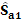 – оценки среднеквадратичного отклонения оценок коэффициентов регрессии, – оценки среднеквадратичного отклонения оценок коэффициентов регрессии,
1.3. R^2 – коэффициент детерминации,
1.4. Sε – оценка среднеквадратичного отклонения ε,
1.5. F – статистика,
1.6. f2 – число степеней свободы,
1.7. RSS – объясненная сумма квадратов отклонений,
1.8. ESS – необъясненная сумма квадратов отклонений.
2.
Тест Дарбина-Уотсона.
2.1. 
3.
Тест Голдфелда – Квандта.
3.1. 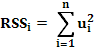 - сумма квадратов остатков. - сумма квадратов остатков.
3.2. 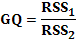
3.3. 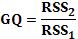
3.4.
4.
F-тест
4.1. 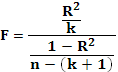
5.
t-критерий Стьюдента
5.1. 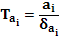
5.2. 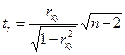
6.
Средняя ошибка аппроксимации
6.1. 
7.
Эластичность
7.1. 
8.
Проверка значимости
8.1. 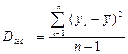
8.2. 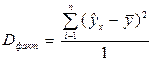
8.3. 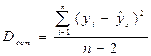
8.4. 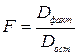
9.
Дисперсия
9.1. 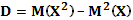
10.
Ср. кв. отклонение
10.1. 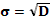
11.
Проверка адекватности
11.1. 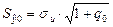
11.2. 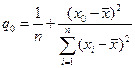
11.3. 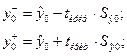
11.4. 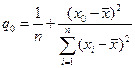
Для проведения анализа данные собраны и сгруппированы в таблице:
| № дня
|
Дата
|
RTS
|
ОАО РусГидро
|
ОАО ЛУКОЙЛ
|
ОАО Сбербанк России
|
ОАО Татнефть
|
ОАО Газпром
|
| HYDR
|
LKOH
|
SBERG
|
TATN
|
GAZP
|
| 1 |
4 май |
1517,83 |
1,67 |
1666,12 |
77,38 |
144,75 |
168,31 |
| 2 |
5 май |
1482,67 |
1,62 |
1656,49 |
75,73 |
141,27 |
163,96 |
| 3 |
6 май |
1450,47 |
1,59 |
1658,37 |
75,30 |
139,96 |
164,94 |
| 4 |
7 май |
1369,91 |
1,52 |
1618,08 |
71,31 |
140,70 |
159,83 |
| 5 |
11 май |
1420,54 |
1,53 |
1606,10 |
74,32 |
132,67 |
159,75 |
| 6 |
12 май |
1485,36 |
1,61 |
1616,29 |
78,85 |
133,87 |
163,76 |
| 7 |
13 май |
1476,03 |
1,62 |
1612,97 |
81,65 |
133,48 |
163,92 |
| 8 |
14 май |
1441,68 |
1,62 |
1596,41 |
78,67 |
129,65 |
160,26 |
| 9 |
17 май |
1422,72 |
1,62 |
1578,90 |
75,96 |
128,49 |
159,61 |
| 10 |
18 май |
1438,94 |
1,64 |
1565,31 |
77,06 |
131,41 |
162,04 |
| 11 |
19 май |
1379,88 |
1,64 |
1537,33 |
74,68 |
129,49 |
158,19 |
| 12 |
20 май |
1303,24 |
1,62 |
1505,25 |
72,85 |
128,40 |
156,15 |
| 13 |
21 май |
1297,91 |
1,53 |
1475,22 |
69,16 |
124,01 |
149,91 |
| 14 |
24 май |
1311,70 |
1,55 |
1476,34 |
70,00 |
125,68 |
150,03 |
| 15 |
25 май |
1226,57 |
1,49 |
1427,46 |
66,19 |
122,73 |
145,75 |
| 16 |
26 май |
1305,25 |
1,54 |
1438,03 |
68,07 |
121,53 |
148,29 |
| 17 |
27 май |
1358,60 |
1,65 |
1482,99 |
70,01 |
125,28 |
156,46 |
| 18 |
28 май |
1366,90 |
1,65 |
1488,47 |
70,86 |
132,14 |
157,31 |
| 19 |
31 май |
1384,59 |
1,66 |
1492,18 |
70,47 |
134,31 |
157,78 |
| 20 |
1 июн |
1373,87 |
1,65 |
1488,92 |
69,26 |
135,26 |
156,41 |
| 21 |
2 июн |
1383,87 |
1,66 |
1525,15 |
70,17 |
134,69 |
160,47 |
| 22 |
3 июн |
1393,12 |
1,68 |
1585,09 |
72,73 |
137,95 |
166,51 |
| 23 |
4 июн |
1360,74 |
1,65 |
1614,23 |
71,41 |
136,47 |
164,04 |
| 24 |
7 июн |
1340,82 |
1,58 |
1602,83 |
69,51 |
130,69 |
159,94 |
| 25 |
8 июн |
1315,61 |
1,59 |
1603,18 |
71,65 |
130,79 |
159,97 |
| 26 |
9 июн |
1334,55 |
1,58 |
1611,34 |
71,74 |
131,54 |
158,85 |
| 27 |
10 июн |
1358,94 |
1,59 |
1636,71 |
72,00 |
136,72 |
157,41 |
| 28 |
11 июн |
1356,79 |
1,62 |
1671,78 |
72,91 |
139,99 |
156,87 |
| 29 |
15 июн |
1396,57 |
1,67 |
1682,50 |
73,84 |
141,50 |
158,39 |
| 30 |
16 июн |
1401,63 |
1,68 |
1708,26 |
76,54 |
142,45 |
158,77 |
| №
|
Дата
|
RTS
|
ОАО РусГидро
|
X
|
Y
|
 |
ui
|
ui
-ui-1
|
(Y-
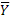 )
2 )
2
|
(Y-
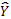 )
2 )
2
|
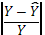 |
| HYDR
|
| 15 |
25 май |
1226,57 |
1,49 |
1226,57 |
1,49 |
1,55 |
0,06 |
0,06 |
0,00 |
0,00 |
0,04 |
| 13 |
21 май |
1297,91 |
1,53 |
1297,91 |
1,53 |
1,58 |
0,05 |
-0,01 |
0,00 |
0,00 |
0,03 |
| 12 |
20 май |
1303,24 |
1,62 |
1303,24 |
1,62 |
1,58 |
-0,04 |
-0,09 |
0,00 |
0,00 |
0,03 |
| 16 |
26 май |
1305,25 |
1,54 |
1305,25 |
1,54 |
1,58 |
0,04 |
0,08 |
0,00 |
0,00 |
0,03 |
| 14 |
24 май |
1311,70 |
1,55 |
1311,70 |
1,55 |
1,58 |
0,03 |
-0,01 |
0,00 |
0,00 |
0,02 |
| 25 |
8 июн |
1315,61 |
1,59 |
1315,61 |
1,59 |
1,59 |
-0,01 |
-0,04 |
0,00 |
0,00 |
0,00 |
| 26 |
9 июн |
1334,55 |
1,58 |
1334,55 |
1,58 |
1,59 |
0,01 |
0,02 |
0,00 |
0,00 |
0,01 |
| 24 |
7 июн |
1340,82 |
1,58 |
1340,82 |
1,58 |
1,60 |
0,02 |
0,01 |
0,00 |
0,00 |
0,01 |
| 28 |
11 июн |
1356,79 |
1,62 |
1356,79 |
1,62 |
1,60 |
-0,02 |
-0,04 |
0,00 |
0,00 |
0,01 |
| 17 |
27 май |
1358,60 |
1,65 |
1358,60 |
1,65 |
1,60 |
-0,05 |
-0,03 |
0,00 |
0,00 |
0,03 |
| 27 |
10 июн |
1358,94 |
1,59 |
1358,94 |
1,59 |
1,60 |
0,02 |
0,07 |
0,00 |
0,00 |
0,01 |
| 23 |
4 июн |
1360,74 |
1,65 |
1360,74 |
1,65 |
1,60 |
-0,05 |
-0,06 |
0,00 |
0,00 |
0,03 |
| 18 |
28 май |
1366,90 |
1,65 |
1366,90 |
1,65 |
1,61 |
-0,04 |
0,00 |
0,00 |
0,00 |
0,03 |
| 4 |
7 май |
1369,91 |
1,52 |
1369,91 |
1,52 |
1,61 |
0,09 |
0,13 |
0,00 |
0,01 |
0,06 |
| 20 |
1 июн |
1373,87 |
1,65 |
1373,87 |
1,65 |
1,61 |
-0,05 |
-0,13 |
0,00 |
0,00 |
0,03 |
| 11 |
19 май |
1379,88 |
1,64 |
1379,88 |
1,64 |
1,61 |
-0,03 |
0,02 |
0,00 |
0,00 |
0,02 |
| 21 |
2 июн |
1383,87 |
1,66 |
1383,87 |
1,66 |
1,61 |
-0,04 |
-0,02 |
0,00 |
0,00 |
0,03 |
| 19 |
31 май |
1384,59 |
1,66 |
1384,59 |
1,66 |
1,61 |
-0,05 |
-0,01 |
0,00 |
0,00 |
0,03 |
| 22 |
3 июн |
1393,12 |
1,68 |
1393,12 |
1,68 |
1,62 |
-0,07 |
-0,02 |
0,00 |
0,00 |
0,04 |
| 29 |
15 июн |
1396,57 |
1,67 |
1396,57 |
1,67 |
1,62 |
-0,06 |
0,01 |
0,00 |
0,00 |
0,03 |
| 30 |
16 июн |
1401,63 |
1,68 |
1401,63 |
1,68 |
1,62 |
-0,06 |
-0,01 |
0,00 |
0,00 |
0,04 |
| 5 |
11 май |
1420,54 |
1,53 |
1420,54 |
1,53 |
1,63 |
0,09 |
0,16 |
0,00 |
0,01 |
0,06 |
| 9 |
17 май |
1422,72 |
1,62 |
1422,72 |
1,62 |
1,63 |
0,01 |
-0,08 |
0,00 |
0,00 |
0,01 |
| 10 |
18 май |
1438,94 |
1,64 |
1438,94 |
1,64 |
1,63 |
-0,01 |
-0,02 |
0,00 |
0,00 |
0,01 |
| 8 |
14 май |
1441,68 |
1,62 |
1441,68 |
1,62 |
1,63 |
0,02 |
0,03 |
0,00 |
0,00 |
0,01 |
| 3 |
6 май |
1450,47 |
1,59 |
1450,47 |
1,59 |
1,64 |
0,05 |
0,03 |
0,00 |
0,00 |
0,03 |
| 7 |
13 май |
1476,03 |
1,62 |
1476,03 |
1,62 |
1,65 |
0,02 |
-0,03 |
0,00 |
0,00 |
0,02 |
| 2 |
5 май |
1482,67 |
1,62 |
1482,67 |
1,62 |
1,65 |
0,03 |
0,01 |
0,00 |
0,00 |
0,02 |
| 6 |
12 май |
1485,36 |
1,61 |
1485,36 |
1,61 |
1,65 |
0,04 |
0,00 |
0,00 |
0,00 |
0,02 |
| 1 |
4 май |
1517,83 |
1,67 |
1517,83 |
1,67 |
1,66 |
0,00 |
-0,04 |
0,00 |
0,00 |
0,00 |
| Сумма: |
0,02 |
0,06 |
0,72 |
| ЛИНЕЙН()
|
Тест Дарбина-Уотсона
|
Тест Голдфелда-Квандта
|
t-критерий Стьюдента
|
| 0,000379 |
1,08702 |
DW |
1,729946 |
RSS1
|
0,027663 |
Та1
= |
2,89575 |
| 0,000131 |
0,181143 |
dl |
1,35 |
RSS2 |
0,031246 |
Та0
= |
6,00091 |
| 0,23046 |
0,045868 |
du |
1,49 |
GQ |
1,129518 |
Tr
= |
2,89575 |
| 8,38537 |
28 |
4-du |
2,51 |
GQ-1
|
0,885334 |
Tkp
= |
2,04841 |
| 0,017642 |
0,058909 |
4-dl |
2,65 |
Fкр
|
2,403447 |
| Оценка a
1
и a0
|
F-тест
|
| Знач |
НГ |
ВГ |
F |
8,38537 |
| a1
|
0,000379 |
0,000112 |
0,000647 |
Fкрит |
3,340386 |
| a0
|
1,08702 |
0,715346 |
1,458694 |
| Средняя ошибка аппроксимации
|
2,40% |
| Эластичность
|
32,53% |
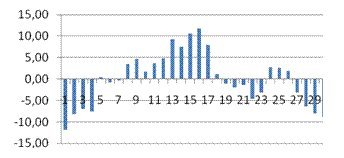
Тест Дарбина-Уотсона.
· du
<DW
<4-
du
, следовательно, автокорреляция отсутствует. Случайные возмущения не зависят друг от друга.
Тест Голдфелда-Квандта
· GQ, GQ-1
<Fкр
– гомоскедастичность.
t-критерий Стьюдента
· ta1
, tа0
> tкр
. ни одним из параметров пренебречь нельзя, оба параметра а0
и а1
являются значимыми.
F-тест
· , следовательно модель является качественной.
Средняя ошибка аппроксимации
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 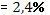 - допустимая ошибка. - допустимая ошибка.
Эластичность
· Расчет коэффициента средней эластичности 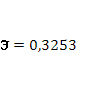 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 32,53%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 32,53%.
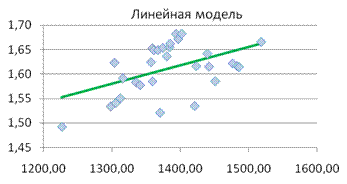 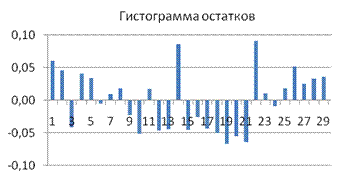
· Проверим адекватность модели используя контролирующую выборку в 40 значений.
| №
|
X
|
Y
|
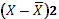 |
Линейн
|
| 1 |
1517,83 |
1,67 |
18809,53472 |
0,000361 |
1,107856 |
| 2 |
1482,67 |
1,62 |
10401,523 |
0,000127 |
0,175597 |
| 3 |
1450,47 |
1,59 |
4870,345005 |
0,236982 |
0,044383 |
| 4 |
1369,91 |
1,52 |
116,0390617 |
8,075224 |
26 |
| 5 |
1420,54 |
1,53 |
1588,648776 |
0,015907 |
0,051216 |
| 6 |
1485,36 |
1,61 |
10957,45378 |
| 7 |
1476,03 |
1,62 |
9091,213862 |
| 8 |
1441,68 |
1,62 |
3720,738576 |
| 9 |
1422,72 |
1,62 |
1767,181433 |
| 10 |
1438,94 |
1,64 |
3393,977919 |
| 11 |
1379,88 |
1,64 |
0,643433163 |
| 12 |
1303,24 |
1,62 |
5997,28549 |
| 13 |
1297,91 |
1,53 |
6851,227633 |
a0
|
a1
|
σu
|
n
|
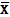 |
n-k
|
| 14 |
1311,70 |
1,55 |
4758,536033 |
1,107856 |
0,000361 |
0,044383 |
28 |
1 380,68 |
26 |
| 15 |
1226,57 |
1,49 |
23750,55258 |
| 16 |
1305,25 |
1,54 |
5690,008176 |
n
|
X0
|
σu
|
∑(Xi-Xср)2
|
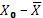 |
q0
|
| 17 |
1358,60 |
1,65 |
487,6210332 |
28 |
1 396,57 |
0,044383 |
122061,8 |
15,89 |
0,037782 |
| 18 |
1366,90 |
1,65 |
189,9474617 |
| 19 |
1384,59 |
1,66 |
15,27134745 |
Sy0
|
ỹ0
|
t крит
|
Y0-
|
Y0+
|
Y0
|
| 20 |
1373,87 |
1,65 |
46,40529031 |
0,045214 |
1,612016 |
2,055529 |
1,519078 |
1,704954 |
1,7 |
| 21 |
1383,87 |
1,66 |
10,16243316 |
| 22 |
1393,12 |
1,68 |
154,7002903 |
| 23 |
1360,74 |
1,65 |
397,6890617 |
| 24 |
1340,82 |
1,58 |
1588,990433 |
a0
|
a1
|
σu
|
n
|
Хср
|
n-k
|
| 25 |
1315,61 |
1,59 |
4234,383776 |
1,107856 |
0,000361 |
0,044383 |
28 |
1 380,68 |
26 |
| 26 |
1334,55 |
1,58 |
2128,174605 |
| 27 |
1358,94 |
1,59 |
472,720776 |
n
|
X0
|
σu
|
∑(Xi-Xср)2
|
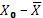 |
q0
|
| 28 |
1356,79 |
1,62 |
570,8344903 |
28 |
1 401,63 |
0,044383 |
122061,8 |
20,95 |
0,039309 |
| 29 |
1396,57 |
1,67 |
| 30 |
1401,63 |
1,68 |
Sy0
|
ỹ0
|
t крит
|
Y0-
|
Y0+
|
Y0
|
| Среднее: |
1380,68 |
0,045247 |
1,613843 |
2,055529 |
1,520836 |
1,706849 |
1,7 |
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
1,08702 |
y = 0,000379 *x + 1,08702 |
Та= |
2,89575 |
| а1
= |
0,00038 |
средние квадрат. отклонения
|
Тв= |
6,00091 |
| Дисперсии Х и У
|
Tr= |
2,89575 |
| S2
х= |
4090,26 |
Sx= |
63,9551 |
Tkp= |
2,04841 |
| S2
у= |
0,00255 |
Sy= |
0,05051 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,48006 |
R2
= |
0,23046 |
| Проверка значимости уравнения регрессии
|
GQ= |
1,12952 |
GQ-1
= |
0,88533 |
| DW= |
1,72995 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт
= |
0,0176 |
Dост
= |
0,0021 |
F= |
8,38537 |
Fкр
= |
3,34039 |
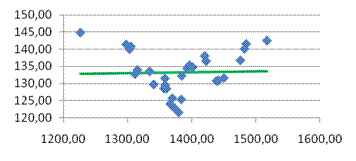
· Сформирована эконометрическая модель в виде линейного уравнения парной регрессии, связывающая величину цены акции с величиной индекса РТС
.
· На основании анализа численного значения коэффициента корреляци
и 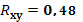 можно сделать вывод о том, что установлена средняя степень связи между стоимостью акции и величиной индекса РТС. можно сделать вывод о том, что установлена средняя степень связи между стоимостью акции и величиной индекса РТС.
· Исходя из коэффициента детерминации 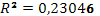 , доля дисперсии цены акции на 23% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 23% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
1381,5262 |
y = 0,139482*x + 1381,526 |
Та= |
0,62294 |
| а1
= |
0,1394818 |
средние квадрат. отклонения
|
Тв= |
4,4601 |
| Дисперсии Х и У
|
Tr= |
0,62294 |
| S2
х= |
4090,2606 |
Sx= |
63,9551 |
Tkp= |
2,04841 |
| S2
у= |
5821,3918 |
Sy= |
76,298 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,1169175 |
R2= |
0,01367 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,99365 |
GQ-1
= |
1,00639 |
| DW= |
0,1814287 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
2387,3019 |
Dост= |
6151,94 |
F= |
0,38806 |
Fкр= |
3,34039 |
 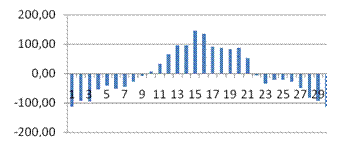
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, tа0
< tкр
. параметры не значимы
· , следовательно модель является не качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 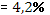 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 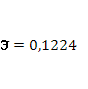 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 12,24%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 12,24%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 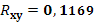 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 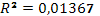 , доля дисперсии цены акции на 1% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 1% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
98,4368 |
y =-0,0184 *x +984368 |
Та= |
-1,8686 |
| а1
= |
-0,0184 |
средние квадрат. отклонения
|
Тв= |
7,2263 |
| Дисперсии Х и У
|
Tr= |
-1,8686 |
| S2
х= |
4090,26 |
Sx= |
63,9551 |
Tkp= |
2,04841 |
| S2
у= |
12,4894 |
Sy= |
3,53403 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
-0,333 |
R2= |
0,11088 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,5347 |
GQ-1
= |
1,87022 |
| DW= |
0,45883 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
41,5439 |
Dост= |
11,8978 |
F= |
3,49173 |
Fкр= |
3,34039 |
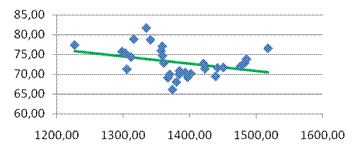 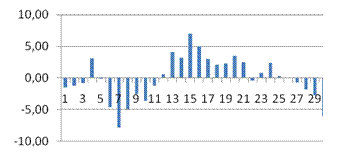
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, tа0
< tкр
. параметры не значимы
· , следовательно модель является качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 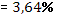 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 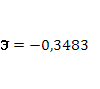 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 34%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 34%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 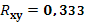 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 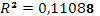 , доля дисперсии цены акции на 11% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 11% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
129,554 |
y = 0,002683 *x +129,5544 |
Та= |
0,15034 |
| а1
= |
0,00268 |
средние квадрат. отклонения
|
Тв= |
5,24701 |
| Дисперсии Х и У
|
Tr= |
0,15034 |
| S2
х= |
4090,26 |
Sx= |
63,9551 |
Tkp= |
2,04841 |
| S2
у= |
36,5133 |
Sy= |
6,04262 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,0284 |
R2= |
0,00081 |
| Проверка значимости уравнения регрессии |
GQ= |
0,70084 |
GQ-1
= |
1,42685 |
| DW= |
0,40126 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
0,8835 |
Dост= |
39,0898 |
F= |
0,0226 |
Fкр= |
3,34039 |
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель является не качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 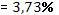 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 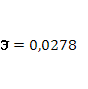 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 2,78%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 2,78%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 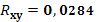 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 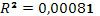 , доля дисперсии цены акции на 0,08% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 0,08% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
5,24491 |
y =-0,00013*x +5,2449 |
Та= |
-1,3871 |
| а1
= |
-0,0001 |
средние квадрат. отклонения
|
Тв= |
40,8691 |
| Дисперсии Х и У
|
Tr= |
-1,3871 |
| S2
х= |
4090,26 |
Sx= |
63,9551 |
Tkp= |
2,04841 |
| S2
у= |
0,00105 |
Sy= |
0,03246 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
-0,2536 |
R2= |
0,06429 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,57106 |
GQ-1
= |
1,75111 |
| DW= |
0,48124 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
51,3533 |
Dост= |
25,8146877 |
F= |
1,92394 |
Fкр= |
3,34039 |
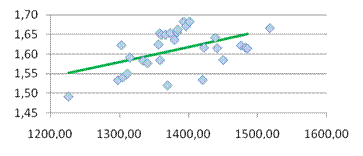 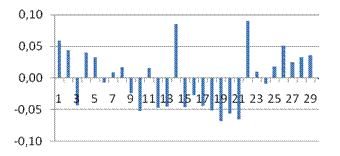
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель является не качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 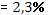 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 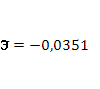 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 3,51%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 3,51%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 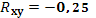 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 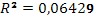 , доля дисперсии цены акции на 0,6% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 0,6% обусловлена дисперсией факторных переменных.
| №
|
Дата
|
RTS
|
ОАО ЛУКОЙЛ
|
X
|
Y
|
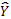 |
ui
|
ui
-ui-1
|
(Y-
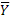 )
2 )
2
|
(Y-
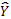 )
2 )
2
|
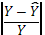 |
| LKOH
|
| 15 |
25 май |
1226,57 |
1666,12 |
7,11 |
7,42 |
1555,15 |
-110,97 |
-110,97 |
365,73 |
12314,41 |
0,07 |
| 13 |
21 май |
1297,91 |
1656,49 |
7,17 |
7,41 |
1563,39 |
-93,11 |
17,86 |
118,64 |
8669,04 |
0,06 |
| 12 |
20 май |
1303,24 |
1658,37 |
7,17 |
7,41 |
1563,98 |
-94,39 |
-1,28 |
105,96 |
8909,09 |
0,06 |
| 16 |
26 май |
1305,25 |
1618,08 |
7,17 |
7,39 |
1564,21 |
-53,87 |
40,52 |
101,38 |
2902,24 |
0,03 |
| 14 |
24 май |
1311,70 |
1606,10 |
7,18 |
7,38 |
1564,93 |
-41,17 |
12,70 |
87,40 |
1695,17 |
0,03 |
| 25 |
8 июн |
1315,61 |
1616,29 |
7,18 |
7,39 |
1565,36 |
-50,92 |
-9,75 |
79,45 |
2593,08 |
0,03 |
| 26 |
9 июн |
1334,55 |
1612,97 |
7,20 |
7,39 |
1567,45 |
-45,52 |
5,40 |
46,55 |
2072,09 |
0,03 |
| 24 |
7 июн |
1340,82 |
1596,41 |
7,20 |
7,38 |
1568,14 |
-28,27 |
17,25 |
37,66 |
799,15 |
0,02 |
| 28 |
11 июн |
1356,79 |
1578,90 |
7,21 |
7,36 |
1569,88 |
-9,02 |
19,25 |
19,38 |
81,38 |
0,01 |
| 17 |
27 май |
1358,60 |
1565,31 |
7,21 |
7,36 |
1570,07 |
4,76 |
13,78 |
17,69 |
22,62 |
0,00 |
| 27 |
10 июн |
1358,94 |
1537,33 |
7,21 |
7,34 |
1570,11 |
32,78 |
28,02 |
17,39 |
1074,51 |
0,02 |
| 23 |
4 июн |
1360,74 |
1505,25 |
7,22 |
7,32 |
1570,30 |
65,05 |
32,27 |
15,80 |
4231,16 |
0,04 |
| 18 |
28 май |
1366,90 |
1475,22 |
7,22 |
7,30 |
1570,96 |
95,75 |
30,70 |
10,98 |
9167,47 |
0,06 |
| 4 |
7 май |
1369,91 |
1476,34 |
7,22 |
7,30 |
1571,29 |
94,94 |
-0,80 |
8,94 |
9014,13 |
0,06 |
| 20 |
1 июн |
1373,87 |
1427,46 |
7,23 |
7,26 |
1571,71 |
144,25 |
49,31 |
6,59 |
20807,61 |
0,10 |
| 11 |
19 май |
1379,88 |
1438,03 |
7,23 |
7,27 |
1572,35 |
134,32 |
-9,93 |
3,71 |
18041,58 |
0,09 |
| 21 |
2 июн |
1383,87 |
1482,99 |
7,23 |
7,30 |
1572,78 |
89,78 |
-44,54 |
2,26 |
8060,56 |
0,06 |
| 19 |
31 май |
1384,59 |
1488,47 |
7,23 |
7,31 |
1572,85 |
84,38 |
-5,40 |
2,03 |
7119,49 |
0,06 |
| 22 |
3 июн |
1393,12 |
1492,18 |
7,24 |
7,31 |
1573,75 |
81,57 |
-2,80 |
0,27 |
6654,12 |
0,05 |
| 29 |
15 июн |
1396,57 |
1488,92 |
7,24 |
7,31 |
1574,12 |
85,19 |
3,62 |
0,03 |
7258,07 |
0,06 |
| 30 |
16 июн |
1401,63 |
1525,15 |
7,25 |
7,33 |
1574,65 |
49,50 |
-35,69 |
0,14 |
2450,69 |
0,03 |
| 5 |
11 май |
1420,54 |
1585,09 |
7,26 |
7,37 |
1576,62 |
-8,47 |
-57,97 |
5,49 |
71,67 |
0,01 |
| 9 |
17 май |
1422,72 |
1614,23 |
7,26 |
7,39 |
1576,85 |
-37,38 |
-28,91 |
6,60 |
1397,32 |
0,02 |
| 10 |
18 май |
1438,94 |
1602,83 |
7,27 |
7,38 |
1578,52 |
-24,31 |
13,07 |
17,97 |
590,88 |
0,02 |
| 8 |
14 май |
1441,68 |
1603,18 |
7,27 |
7,38 |
1578,80 |
-24,39 |
-0,08 |
20,43 |
594,63 |
0,02 |
| 3 |
6 май |
1450,47 |
1611,34 |
7,28 |
7,38 |
1579,69 |
-31,64 |
-7,26 |
29,34 |
1001,39 |
0,02 |
| 7 |
13 май |
1476,03 |
1636,71 |
7,30 |
7,40 |
1582,27 |
-54,43 |
-22,79 |
63,93 |
2963,11 |
0,03 |
| 2 |
5 май |
1482,67 |
1671,78 |
7,30 |
7,42 |
1582,94 |
-88,85 |
-34,41 |
74,98 |
7894,01 |
0,05 |
| 6 |
12 май |
1485,36 |
1682,50 |
7,30 |
7,43 |
1583,20 |
-99,29 |
-10,45 |
79,69 |
9859,16 |
0,06 |
| 1 |
4 май |
1517,83 |
1708,26 |
7,33 |
7,44 |
1586,40 |
-121,86 |
-22,56 |
147,06 |
14849,11 |
0,07 |
| Сумма: |
1493,47 |
173158,93 |
1,27 |
| ЛИНЕЙН()
|
Тест Дарбина-Уотсона
|
Тест Голдфелда-Квандта
|
t-критерий Стьюдента
|
| 0,093382 |
6,685202 |
DW |
0,177693 |
RSS1
|
84353,13 |
Та1
= |
0,47084 |
| 0,198328 |
1,433968 |
dl |
1,35 |
RSS2
|
88805,8 |
Та0
= |
4,66203 |
| 0,007855 |
0,050377 |
du |
1,49 |
GQ |
1,052786 |
Tr
= |
0,47084 |
| 0,221695 |
28 |
4-du |
2,51 |
GQ-1
|
0,949861 |
Tkp
= |
2,04841 |
| 0,000563 |
0,07106 |
4-dl |
2,65 |
Fкр
|
2,403447 |
| Оценка a
1
и a0
|
F-тест
|
| Знач |
НГ |
ВГ |
F |
0,221695 |
| a1 |
0,093382 |
-0,31166 |
0,498421 |
Fкрит |
3,340386 |
| a0 |
6,685202 |
3,742942 |
9,627462 |
| Средняя ошибка аппроксимации
|
4,23% |
| Эластичность
|
9,17% |
Тест Дарбина-Уотсона.
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
Тест Голдфелда-Квандта
· GQ, GQ-1
<Fкр
– гомоскедастичность.
t-критерий Стьюдента
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
F-тест
· , следовательно модель не является качественной.
Средняя ошибка аппроксимации
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 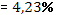 - допустимая ошибка. - допустимая ошибка.
Эластичность
· Расчет коэффициента средней эластичности 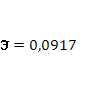 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 9,17%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 9,17%.
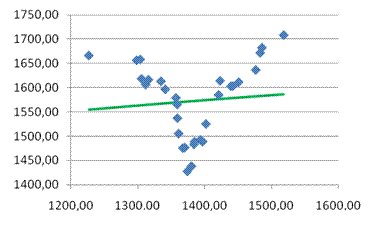 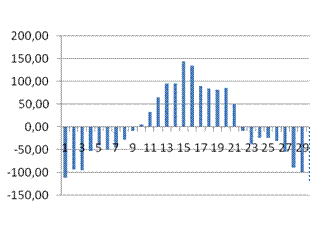
· Проверим адекватность модели используя контролирующую выборку в 40 значений.
| №
|
X
|
Y
|
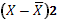 |
Линейн
|
| 1 |
0,000659 |
1708,262 |
4,50308E-09 |
-201352 |
1725,25 |
| 2 |
0,000674 |
1671,785 |
2,65033E-09 |
429896,3 |
312,4374 |
| 3 |
0,000689 |
1611,339 |
1,33288E-09 |
0,008367 |
79,15949 |
| 4 |
0,00073 |
1476,344 |
1,62785E-11 |
0,219373 |
26 |
| 5 |
0,000704 |
1585,087 |
4,83237E-10 |
1374,641 |
162921,8 |
| 6 |
0,000673 |
1682,498 |
2,77759E-09 |
| 7 |
0,000677 |
1636,707 |
2,34714E-09 |
| 8 |
0,000694 |
1603,183 |
1,04362E-09 |
| 9 |
0,000703 |
1614,228 |
5,31824E-10 |
| 10 |
0,000695 |
1602,825 |
9,60026E-10 |
| 11 |
0,000725 |
1438,033 |
1,53662E-12 |
| 12 |
0,000767 |
1658,372 |
1,71214E-09 |
| 13 |
0,00077 |
1656,493 |
1,98284E-09 |
a0
|
a1
|
σu
|
n
|
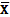 |
n-k
|
| 14 |
0,000762 |
1606,101 |
1,32708E-09 |
1725,25 |
-201352 |
79,15949 |
28 |
0,00072594 |
26 |
| 15 |
0,000815 |
1666,124 |
7,98187E-09 |
| 16 |
0,000766 |
1618,081 |
1,61575E-09 |
n
|
X0
|
σu
|
∑(Xi-Xср)2
|
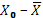 |
q0
|
| 17 |
0,000736 |
1565,315 |
1,02243E-10 |
28 |
0,000716 |
79,15949 |
3,39E-08 |
-9,90029E-06 |
0,038605 |
| 18 |
0,000732 |
1475,218 |
3,18334E-11 |
| 19 |
0,000722 |
1488,475 |
1,37258E-11 |
Sy0
|
ỹ0
|
t крит
|
Y0-
|
Y0+
|
Y0
|
| 20 |
0,000728 |
1427,462 |
3,72722E-12 |
80,673 |
1581,074 |
2,055529 |
1415,248 |
1746,899798 |
1488,923 |
| 21 |
0,000723 |
1482,995 |
1,10827E-11 |
| 22 |
0,000718 |
1492,181 |
6,60489E-11 |
| 23 |
0,000735 |
1505,255 |
8,01731E-11 |
| 24 |
0,000746 |
1596,41 |
3,94895E-10 |
a0
|
a1
|
σu
|
n
|
Хср
|
n-k
|
| 25 |
0,00076 |
1616,286 |
1,16714E-09 |
1725,25 |
-201352 |
79,15949 |
28 |
0,00072594 |
26 |
| 26 |
0,000749 |
1612,975 |
5,46435E-10 |
| 27 |
0,000736 |
1537,328 |
9,85524E-11 |
n
|
X0
|
σu
|
∑(Xi-Xср)2
|
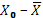 |
q0
|
| 28 |
0,000737 |
1578,897 |
1,23064E-10 |
28 |
0,000713 |
79,15949 |
3,39E-08 |
-1,24853E-05 |
0,040312 |
| 29 |
0,000716 |
1488,923 |
9,80158E-11 |
| 30 |
0,000713 |
1525,145 |
1,55882E-10 |
Sy0
|
ỹ0
|
t крит
|
Y0-
|
Y0+
|
Y0
|
| Среднее:: |
0,000726
|
80,73925 |
1581,595 |
2,055529 |
1415,633 |
1747,556472 |
1525,145 |
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
6,6852018 |
y = x0,0933816
+ 6,6852018 |
Та= |
0,47084 |
| а1
= |
0,0933816 |
средние квадрат. отклонения
|
4,66203 |
6,00091 |
| Дисперсии Х и У
|
Tr= |
0,47084 |
| S2
х= |
0,0021507 |
Sx= |
0,04638 |
Tkp= |
2,04841 |
| S2
у= |
0,0023874 |
Sy= |
0,04886 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,0886311 |
R2
= |
0,00786 |
| Проверка значимости уравнения регрессии
|
GQ= |
1,05279 |
GQ-1
= |
0,94986 |
| DW= |
0,1776926 |
1,49 |
1,35 |
Du= |
1,49 |
| Dфакт
= |
1493,4682 |
0,22169 |
6184,25 |
F= |
0,22169 |
Fкр
= |
3,34039 |
· Сформирована эконометрическая модель в виде степенного уравнения парной регрессии, связывающая величину цены акции с величиной индекса РТС.
· На основании анализа численного значения коэффициента корреляции 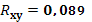 можно сделать вывод о том, что связи между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что связи между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 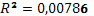 , доля дисперсии цены акции на 0,7% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 0,7% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
-1,9745 |
y =x0,33898
-1,9745 |
Та= |
3,02398 |
| а1
= |
0,33898 |
средние квадрат. отклонения
|
Тв= |
-2,4362 |
| Дисперсии Х и У
|
Tr= |
3,02398 |
| S2
х= |
0,00215 |
Sx= |
0,04638 |
Tkp= |
2,04841 |
| S2
у= |
0,001 |
Sy= |
0,03168 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,49617 |
R2= |
0,24619 |
| Проверка значимости уравнения регрессии
|
GQ= |
1,17198 |
GQ-1
= |
0,85326 |
| DW= |
1,73531 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
0,0192 |
Dост= |
0,00208 |
F= |
9,14443 |
Fкр= |
3,34039 |
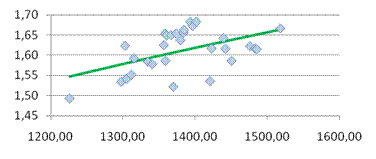 
· du
<DW
<4-
du
, следовательно, автокорреляция отсутствует. Случайные возмущения не зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, tа0
> tкр
. параметры значимы.
· , следовательно модель является качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии  - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 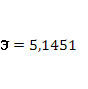 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 514%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 514%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 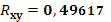 можно сделать вывод о том, что зависимость между стоимостью акции и величиной индекса РТС средняя. можно сделать вывод о том, что зависимость между стоимостью акции и величиной индекса РТС средняя.
· Исходя из коэффициента детерминации 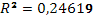 , доля дисперсии цены акции на 24% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 24% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
6,82501 |
y = x-0,3507
+ 6,82501 |
Та= |
-1,9051 |
| а1
= |
-0,3507 |
средние квадрат. отклонения
|
Тв= |
5,12797 |
| Дисперсии Х и У
|
Tr= |
-1,9051 |
| S2
х= |
0,00215 |
Sx= |
0,04638 |
Tkp= |
2,04841 |
| S2
у= |
0,00231 |
Sy= |
0,04801 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
-0,3388 |
R2= |
0,11475 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,5122 |
GQ-1
= |
1,95235 |
| DW= |
0,46154 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
42,4612 |
Dост= |
11,7598 |
F= |
3,62957 |
Fкр= |
3,34039 |
 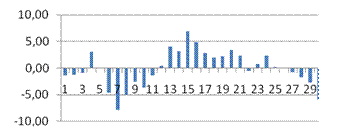
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель является качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 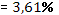 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 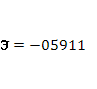 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 59%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 59%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 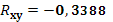 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 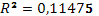 , доля дисперсии цены акции на 11,475% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 11,475% обусловлена дисперсией факторных переменных.
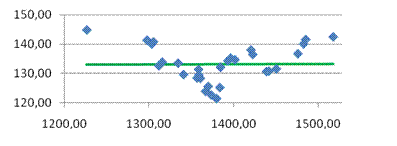
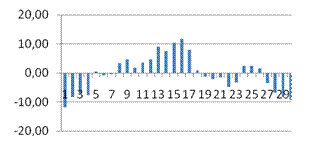
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
4,82811 |
y = x0,00874
+ 4,82811 |
Та= |
0,04715 |
| а1
= |
0,00874 |
средние квадрат. отклонения
|
Тв= |
3,60338 |
| Дисперсии Х и У
|
Tr= |
0,04715 |
| S2
х= |
0,00215 |
Sx= |
0,04638 |
Tkp= |
2,04841 |
| S2
у= |
0,00207 |
Sy= |
0,04548 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,00891 |
R2= |
7,9E-05 |
| Проверка значимости уравнения регрессии |
GQ= |
0,73863 |
GQ-1
= |
1,35386 |
| DW= |
0,39704 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
0,6539 |
Dост= |
39,1412 |
F= |
0,00222 |
Fкр= |
3,34039 |
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель является не качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 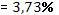 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 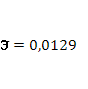 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 1%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 1%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 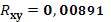 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 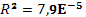 , доля дисперсии цены акции практически не обусловлена дисперсией факторных переменных. , доля дисперсии цены акции практически не обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
6,41465 |
y = x-0,1864
+ 6,41465 |
Та= |
-1,462 |
| а1
= |
-0,1864 |
средние квадрат. отклонения
|
Тв= |
6,95948 |
| Дисперсии Х и У
|
Tr= |
-1,462 |
| S2
х= |
0,00215 |
Sx= |
0,04638 |
Tkp= |
2,04841 |
| S2
у= |
0,00105 |
Sy= |
0,03246 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
-0,2663 |
R2= |
0,07093 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,58543 |
GQ-1
= |
1,70814 |
| DW= |
0,4776 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
56,6954 |
Dост= |
25,6173864 |
F= |
2,13756 |
Fкр= |
3,34039 |
 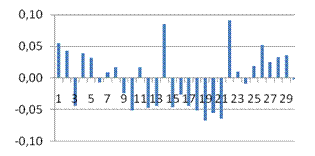
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель является не качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 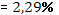 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 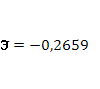 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 26,59%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 26,59%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 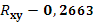 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 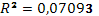 , доля дисперсии цены акции на 0,7% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 0,7% обусловлена дисперсией факторных переменных.
| №
|
Дата
|
RTS
|
ОАО Сбербанк России
|
X
|
Y
|
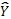 |
ui
|
ui
-ui-1
|
(Y-
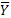 )
2 )
2
|
(Y-
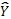 )
2 )
2
|
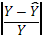 |
| SBERG
|
| 15 |
25 май |
1226,57 |
77,38 |
1226,57 |
4,35 |
75,76 |
-1,63 |
-1,63 |
7,54 |
2,64 |
0,02 |
| 13 |
21 май |
1297,91 |
75,73 |
1297,91 |
4,33 |
74,44 |
-1,29 |
0,33 |
2,05 |
1,67 |
0,02 |
| 12 |
20 май |
1303,24 |
75,30 |
1303,24 |
4,32 |
74,35 |
-0,95 |
0,34 |
1,78 |
0,91 |
0,01 |
| 16 |
26 май |
1305,25 |
71,31 |
1305,25 |
4,27 |
74,31 |
3,00 |
3,95 |
1,69 |
8,99 |
0,04 |
| 14 |
24 май |
1311,70 |
74,32 |
1311,70 |
4,31 |
74,19 |
-0,13 |
-3,13 |
1,40 |
0,02 |
0,00 |
| 25 |
8 июн |
1315,61 |
78,85 |
1315,61 |
4,37 |
74,12 |
-4,73 |
-4,60 |
1,23 |
22,40 |
0,06 |
| 26 |
9 июн |
1334,55 |
81,65 |
1334,55 |
4,40 |
73,78 |
-7,88 |
-3,15 |
0,59 |
62,06 |
0,10 |
| 24 |
7 июн |
1340,82 |
78,67 |
1340,82 |
4,37 |
73,66 |
-5,01 |
2,87 |
0,43 |
25,07 |
0,06 |
| 28 |
11 июн |
1356,79 |
75,96 |
1356,79 |
4,33 |
73,38 |
-2,58 |
2,43 |
0,13 |
6,66 |
0,03 |
| 17 |
27 май |
1358,60 |
77,06 |
1358,60 |
4,34 |
73,34 |
-3,72 |
-1,14 |
0,11 |
13,82 |
0,05 |
| 27 |
10 июн |
1358,94 |
74,68 |
1358,94 |
4,31 |
73,34 |
-1,34 |
2,38 |
0,11 |
1,80 |
0,02 |
| 23 |
4 июн |
1360,74 |
72,85 |
1360,74 |
4,29 |
73,30 |
0,46 |
1,80 |
0,09 |
0,21 |
0,01 |
| 18 |
28 май |
1366,90 |
69,16 |
1366,90 |
4,24 |
73,19 |
4,04 |
3,58 |
0,03 |
16,30 |
0,06 |
| 4 |
7 май |
1369,91 |
70,00 |
1369,91 |
4,25 |
73,14 |
3,14 |
-0,90 |
0,02 |
9,87 |
0,04 |
| 20 |
1 июн |
1373,87 |
66,19 |
1373,87 |
4,19 |
73,07 |
6,88 |
3,73 |
0,00 |
47,29 |
0,10 |
| 11 |
19 май |
1379,88 |
68,07 |
1379,88 |
4,22 |
72,96 |
4,89 |
-1,99 |
0,00 |
23,92 |
0,07 |
| 21 |
2 июн |
1383,87 |
70,01 |
1383,87 |
4,25 |
72,89 |
2,88 |
-2,01 |
0,01 |
8,30 |
0,04 |
| 19 |
31 май |
1384,59 |
70,86 |
1384,59 |
4,26 |
72,88 |
2,02 |
-0,86 |
0,02 |
4,09 |
0,03 |
| 22 |
3 июн |
1393,12 |
70,47 |
1393,12 |
4,26 |
72,73 |
2,26 |
0,24 |
0,08 |
5,10 |
0,03 |
| 29 |
15 июн |
1396,57 |
69,26 |
1396,57 |
4,24 |
72,66 |
3,40 |
1,15 |
0,12 |
11,59 |
0,05 |
| 30 |
16 июн |
1401,63 |
70,17 |
1401,63 |
4,25 |
72,57 |
2,40 |
-1,00 |
0,19 |
5,77 |
0,03 |
| 5 |
11 май |
1420,54 |
72,73 |
1420,54 |
4,29 |
72,24 |
-0,49 |
-2,89 |
0,60 |
0,24 |
0,01 |
| 9 |
17 май |
1422,72 |
71,41 |
1422,72 |
4,27 |
72,20 |
0,78 |
1,28 |
0,66 |
0,62 |
0,01 |
| 10 |
18 май |
1438,94 |
69,51 |
1438,94 |
4,24 |
71,91 |
2,40 |
1,62 |
1,20 |
5,77 |
0,03 |
| 8 |
14 май |
1441,68 |
71,65 |
1441,68 |
4,27 |
71,86 |
0,21 |
-2,19 |
1,31 |
0,04 |
0,00 |
| 3 |
6 май |
1450,47 |
71,74 |
1450,47 |
4,27 |
71,71 |
-0,04 |
-0,25 |
1,69 |
0,00 |
0,00 |
| 7 |
13 май |
1476,03 |
72,00 |
1476,03 |
4,28 |
71,26 |
-0,74 |
-0,70 |
3,06 |
0,54 |
0,01 |
| 2 |
5 май |
1482,67 |
72,91 |
1482,67 |
4,29 |
71,15 |
-1,77 |
-1,03 |
3,47 |
3,12 |
0,02 |
| 6 |
12 май |
1485,36 |
73,84 |
1485,36 |
4,30 |
71,10 |
-2,74 |
-0,97 |
3,65 |
7,51 |
0,04 |
| 1 |
4 май |
1517,83 |
76,54 |
1517,83 |
4,34 |
70,54 |
-6,00 |
-3,26 |
6,12 |
36,02 |
0,08 |
| Сумма: |
39,39 |
332,33 |
1,09 |
| ЛИНЕЙН()
|
Тест Дарбина-Уотсона
|
Тест Голдфелда-Квандта
|
t-критерий Стьюдента
|
| -0,00025 |
4,628202 |
DW |
0,460084 |
RSS1
|
219,6966 |
Та1
= |
-1,8282 |
| 0,000134 |
0,185499 |
dl |
1,35 |
RSS2 |
112,6336 |
Та0
= |
24,9501 |
| 0,10664 |
0,046971 |
du |
1,49 |
GQ |
0,512678 |
Tr
= |
-1,8282 |
| 3,342357 |
28 |
4-du |
2,51 |
GQ-1
|
1,950543 |
Tkp
= |
2,04841 |
| 0,007374 |
0,061776 |
4-dl |
2,65 |
Fкр
|
2,403447 |
| Оценка a
1
и a0
|
F-тест
|
| Знач |
НГ |
ВГ |
F |
3,342357 |
| a1
|
-0,00025 |
-0,00052 |
2,87E-05 |
Fкрит |
3,340386 |
| a0
|
4,628202 |
4,24759 |
5,008814 |
| Средняя ошибка аппроксимации
|
3,64% |
| Эластичность
|
-7,9% |
Тест Дарбина-Уотсона.
· dl
>DW
, следовательно, присутствует автокорреляция отсутствует. Случайные возмущения зависят друг от друга.
Тест Голдфелда-Квандта
· GQ, GQ-1
<Fкр
– гомоскедастичность.
t-критерий Стьюдента
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
F-тест
· , следовательно модель является качественной.
Средняя ошибка аппроксимации
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 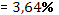 - допустимая ошибка. - допустимая ошибка.
Эластичность
· Расчет коэффициента средней эластичности 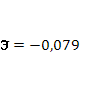 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 7,9%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 7,9%.
 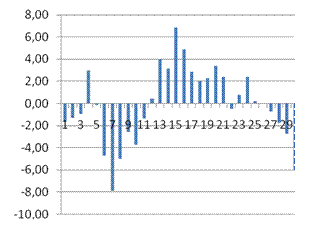
· Проверим адекватность модели используя контролирующую выборку в 40 значений.
| №
|
X
|
Y
|
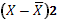 |
Линейн
|
| 1 |
1517,83 |
4,33777 |
18809,53472 |
-0,00023 |
4,614519 |
| 2 |
1482,67 |
4,289276 |
10401,523 |
0,000135 |
0,187002 |
| 3 |
1450,47 |
4,273116 |
4870,345005 |
0,102498 |
0,047266 |
| 4 |
1369,91 |
4,248472 |
116,0390617 |
2,969305 |
26 |
| 5 |
1420,54 |
4,286735 |
1588,648776 |
0,006634 |
0,058085 |
| 6 |
1485,36 |
4,301892 |
10957,45378 |
| 7 |
1476,03 |
4,276664 |
9091,213862 |
| 8 |
1441,68 |
4,271845 |
3720,738576 |
| 9 |
1422,72 |
4,268506 |
1767,181433 |
| 10 |
1438,94 |
4,241492 |
3393,977919 |
| 11 |
1379,88 |
4,220548 |
0,643433163 |
| 12 |
1303,24 |
4,321445 |
5997,28549 |
| 13 |
1297,91 |
4,327235 |
6851,227633 |
a0
|
a1
|
σu
|
n
|
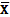 |
n-k
|
| 14 |
1311,7 |
4,308416 |
4758,536033 |
4,614519 |
-0,00023 |
0,047266 |
28 |
1 380,68 |
26 |
| 15 |
1226,57 |
4,348755 |
23750,55258 |
| 16 |
1305,25 |
4,267049 |
5690,008176 |
n
|
X0
|
σu
|
∑(Xi-Xср)2
|
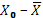 |
q0
|
| 17 |
1358,6 |
4,344591 |
487,6210332 |
28 |
1 396,57 |
0,047266 |
122061,8 |
15,89 |
0,037782 |
| 18 |
1366,9 |
4,236368 |
189,9474617 |
| 19 |
1384,59 |
4,260642 |
15,27134745 |
Sy0
|
ỹ0
|
t крит
|
Y0-
|
Y0+
|
Y0
|
| 20 |
1373,87 |
4,192568 |
46,40529031 |
0,04815 |
4,288947 |
2,055529 |
4,189973 |
4,387922 |
4,2 |
| 21 |
1383,87 |
4,248616 |
10,16243316 |
| 22 |
1393,12 |
4,25514 |
154,7002903 |
| 23 |
1360,74 |
4,288393 |
397,6890617 |
| 24 |
1340,82 |
4,365267 |
1588,990433 |
a0
|
a1
|
σu
|
n
|
Хср
|
n-k
|
| 25 |
1315,61 |
4,36758 |
4234,383776 |
4,614519 |
-0,00023 |
0,047266 |
28 |
1 380,68 |
26 |
| 26 |
1334,55 |
4,402498 |
2128,174605 |
| 27 |
1358,94 |
4,313184 |
472,720776 |
n
|
X0
|
σu
|
∑(Xi-Xср)2
|
 |
q0
|
| 28 |
1356,79 |
4,330164 |
570,8344903 |
28 |
1 401,63 |
0,047266 |
122061,8 |
20,95 |
0,039309 |
| 29 |
1396,57 |
4,237858 |
| 30 |
1401,63 |
4,250938 |
Sy0
|
ỹ0
|
t крит
|
Y0-
|
Y0+
|
Y0
|
| Среднее: |
1380,68 |
0,048186 |
4,287768 |
2,055529 |
4,18872 |
4,386815 |
4,3 |
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
4,6282 |
y = -0,0002x
+ 4,6282 |
Та= |
-1,8282 |
| а1
= |
-0,0002 |
средние квадрат. отклонения
|
Тв= |
24,9501 |
| Дисперсии Х и У
|
Tr= |
-1,8282 |
| S2
х= |
4090,26 |
Sx= |
63,9551 |
Tkp= |
2,04841 |
| S2
у= |
0,00231 |
Sy= |
0,04801 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
-0,3266 |
R2= |
0,10664 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,51268 |
GQ-1
= |
1,95054 |
| DW= |
0,46008 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
39,3874 |
Dост= |
11,8689 |
F= |
3,34236 |
Fкр= |
3,34039 |
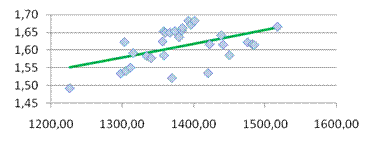
· Сформирована эконометрическая модель в виде линейного уравнения парной регрессии, связывающая величину цены акции с величиной индекса РТС.
· На основании анализа численного значения коэффициента корреляции 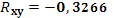 можно сделать вывод о том, что связи между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что связи между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 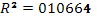 , доля дисперсии цены акции на 10% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 10% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
0,14487 |
y = 0,00024x
+ 0,14487 |
Та= |
2,92833 |
| а1
= |
0,00024 |
средние квадрат. отклонения
|
Тв= |
1,2784 |
| Дисперсии Х и У
|
Tr= |
2,92833 |
| S2
х= |
4090,26 |
Sx= |
63,9551 |
Tkp= |
2,04841 |
| S2
у= |
0,001 |
Sy= |
0,03168 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,4842 |
R2= |
0,23445 |
| Проверка значимости уравнения регрессии
|
GQ= |
1,14827 |
GQ-1
= |
0,87088 |
| DW= |
1,7191 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
0,0183 |
Dост= |
0,00211 |
F= |
8,57512 |
Fкр= |
3,34039 |
 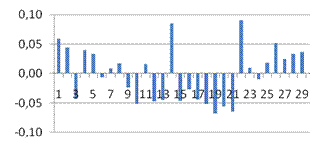
· du
<DW
<4-
du
, следовательно, автокорреляция отсутствует. Случайные возмущения не зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, tа0
> tкр
. параметры значимы, пренебречь ими нельзя.
· , следовательно модель является качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии  - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 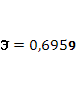 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 69,59%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 69,59%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 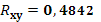 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 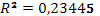 , доля дисперсии цены акции на 23,% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 23,% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
7,2421846 |
y = 0,00008552 x
+ 7,2421846 |
Та= |
0,59606 |
| а1
= |
8,552E-05 |
средние квадрат. отклонения
|
Тв= |
36,4883 |
| Дисперсии Х и У
|
Tr= |
0,59606 |
| S2
х= |
4090,2606 |
Sx= |
63,9551 |
Tkp= |
2,04841 |
| S2
у= |
0,0023874 |
Sy= |
0,04886 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,1119375 |
R2= |
0,01253 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,99596 |
GQ-1
= |
1,00406 |
| DW= |
0,1826641 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
2321,2922 |
Dост= |
6151,8 |
F= |
0,35529 |
Fкр= |
3,34039 |
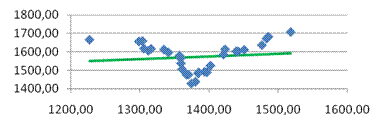 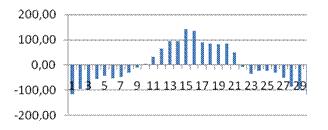
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, tа0
> tкр
. параметры значимы, пренебречь ими нельзя.
· , следовательно модель не является качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 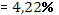 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 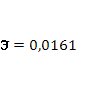 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 1,61%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 1,61%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции  можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 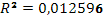 , доля дисперсии цены акции на 1% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 1% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
4,85971 |
y = 0,000023x
+ 4,85971 |
Та= |
0,17011 |
| а1
= |
2,3E-05 |
средние квадрат. отклонения
|
Тв= |
26,1546 |
| Дисперсии Х и У
|
Tr= |
0,17011 |
| S2
х= |
4090,26 |
Sx= |
63,9551 |
Tkp= |
2,04841 |
| S2
у= |
0,00207 |
Sy= |
0,04548 |
| Коэффициент парной корреляции |
Коэффициент детерминации |
| Rxy= |
0,03213 |
R2= |
0,00103 |
| Проверка значимости уравнения регрессии |
GQ= |
0,70281 |
GQ-1
= |
1,42286 |
| DW= |
0,40541 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
1,7008 |
Dост= |
39,1087 |
F= |
0,02894 |
Fкр= |
3,34039 |
 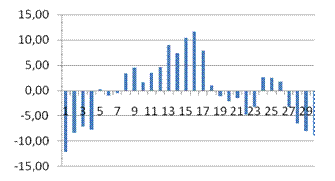
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель является не качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии  - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 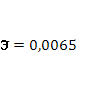 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 0,65%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 0,65%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 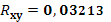 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 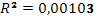 , доля дисперсии цены акции на 0,1% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 0,1% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
5,24491 |
y =-0,0001x
+5,24491 |
Та= |
-1,3871 |
| а1
= |
-0,0001 |
средние квадрат. отклонения
|
Тв= |
40,8691 |
| Дисперсии Х и У
|
Tr= |
-1,3871 |
| S2
х= |
4090,26 |
Sx= |
63,9551 |
Tkp= |
2,04841 |
| S2
у= |
0,00105 |
Sy= |
0,03246 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
-0,2536 |
R2= |
0,06429 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,57106 |
GQ-1
= |
1,75111 |
| DW= |
0,48124 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
51,3533 |
Dост= |
25,8146877 |
F= |
1,92394 |
Fкр= |
3,34039 |
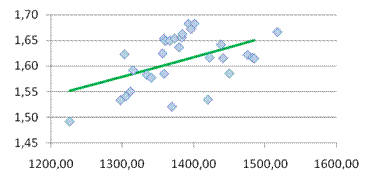 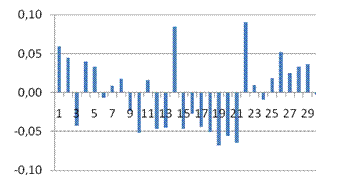
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель является не качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 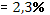 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 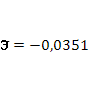 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 3,51%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 3,51%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 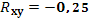 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 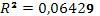 , доля дисперсии цены акции на 0,6% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 0,6% обусловлена дисперсией факторных переменных.
| №
|
Дата
|
RTS
|
ОАО Татнефть
|
X
|
Y
|
 |
ui
|
ui
-ui-1
|
(Y-
 )
2 )
2
|
(Y-
 )
2 )
2
|
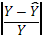 |
TATN
|
| 15 |
25 май |
1226,57 |
144,75 |
0,00082 |
144,75 |
133,57 |
-11,18 |
-11,18 |
0,09 |
124,95 |
0,08 |
| 13 |
21 май |
1297,91 |
141,27 |
0,00077 |
141,27 |
133,42 |
-7,86 |
3,32 |
0,02 |
61,74 |
0,06 |
| 12 |
20 май |
1303,24 |
139,96 |
0,00077 |
139,96 |
133,41 |
-6,56 |
1,30 |
0,02 |
42,98 |
0,05 |
| 16 |
26 май |
1305,25 |
140,70 |
0,00077 |
140,70 |
133,40 |
-7,30 |
-0,74 |
0,02 |
53,27 |
0,05 |
| 14 |
24 май |
1311,70 |
132,67 |
0,00076 |
132,67 |
133,39 |
0,72 |
8,01 |
0,02 |
0,51 |
0,01 |
| 25 |
8 июн |
1315,61 |
133,87 |
0,00076 |
133,87 |
133,38 |
-0,49 |
-1,21 |
0,01 |
0,24 |
0,00 |
| 26 |
9 июн |
1334,55 |
133,48 |
0,00075 |
133,48 |
133,34 |
-0,13 |
0,36 |
0,01 |
0,02 |
0,00 |
| 24 |
7 июн |
1340,82 |
129,65 |
0,00075 |
129,65 |
133,33 |
3,68 |
3,81 |
0,00 |
13,55 |
0,03 |
| 28 |
11 июн |
1356,79 |
128,49 |
0,00074 |
128,49 |
133,30 |
4,82 |
1,13 |
0,00 |
23,19 |
0,04 |
| 17 |
27 май |
1358,60 |
131,41 |
0,00074 |
131,41 |
133,30 |
1,89 |
-2,92 |
0,00 |
3,59 |
0,01 |
| 27 |
10 июн |
1358,94 |
129,49 |
0,00074 |
129,49 |
133,30 |
3,81 |
1,91 |
0,00 |
14,49 |
0,03 |
| 23 |
4 июн |
1360,74 |
128,40 |
0,00073 |
128,40 |
133,30 |
4,89 |
1,08 |
0,00 |
23,93 |
0,04 |
| 18 |
28 май |
1366,90 |
124,01 |
0,00073 |
124,01 |
133,28 |
9,27 |
4,38 |
0,00 |
85,96 |
0,07 |
| 4 |
7 май |
1369,91 |
125,68 |
0,00073 |
125,68 |
133,28 |
7,60 |
-1,67 |
0,00 |
57,81 |
0,06 |
| 20 |
1 июн |
1373,87 |
122,73 |
0,00073 |
122,73 |
133,27 |
10,55 |
2,94 |
0,00 |
111,23 |
0,09 |
| 11 |
19 май |
1379,88 |
121,53 |
0,00072 |
121,53 |
133,26 |
11,73 |
1,18 |
0,00 |
137,57 |
0,10 |
| 21 |
2 июн |
1383,87 |
125,28 |
0,00072 |
125,28 |
133,25 |
7,97 |
-3,76 |
0,00 |
63,55 |
0,06 |
| 19 |
31 май |
1384,59 |
132,14 |
0,00072 |
132,14 |
133,25 |
1,11 |
-6,86 |
0,00 |
1,23 |
0,01 |
| 22 |
3 июн |
1393,12 |
134,31 |
0,00072 |
134,31 |
133,24 |
-1,07 |
-2,18 |
0,00 |
1,15 |
0,01 |
| 29 |
15 июн |
1396,57 |
135,26 |
0,00072 |
135,26 |
133,23 |
-2,03 |
-0,96 |
0,00 |
4,13 |
0,02 |
| 30 |
16 июн |
1401,63 |
134,69 |
0,00071 |
134,69 |
133,22 |
-1,47 |
0,57 |
0,00 |
2,16 |
0,01 |
| 5 |
11 май |
1420,54 |
137,95 |
0,00070 |
137,95 |
133,19 |
-4,76 |
-3,29 |
0,01 |
22,68 |
0,03 |
| 9 |
17 май |
1422,72 |
136,47 |
0,00070 |
136,47 |
133,19 |
-3,28 |
1,48 |
0,01 |
10,75 |
0,02 |
| 10 |
18 май |
1438,94 |
130,69 |
0,00069 |
130,69 |
133,16 |
2,47 |
5,75 |
0,01 |
6,12 |
0,02 |
| 8 |
14 май |
1441,68 |
130,79 |
0,00069 |
130,79 |
133,15 |
2,37 |
-0,11 |
0,01 |
5,60 |
0,02 |
| 3 |
6 май |
1450,47 |
131,54 |
0,00069 |
131,54 |
133,14 |
1,60 |
-0,77 |
0,01 |
2,55 |
0,01 |
| 7 |
13 май |
1476,03 |
136,72 |
0,00068 |
136,72 |
133,10 |
-3,62 |
-5,21 |
0,03 |
13,09 |
0,03 |
| 2 |
5 май |
1482,67 |
139,99 |
0,00067 |
139,99 |
133,09 |
-6,90 |
-3,28 |
0,03 |
47,61 |
0,05 |
| 6 |
12 май |
1485,36 |
141,50 |
0,00067 |
141,50 |
133,09 |
-8,41 |
-1,51 |
0,03 |
70,80 |
0,06 |
| 1 |
4 май |
1517,83 |
142,45 |
0,00066 |
142,45 |
133,04 |
-9,41 |
-1,00 |
0,05 |
88,54 |
0,07 |
| Сумма: |
0,02 |
0,06 |
0,72 |
| ЛИНЕЙН()
|
Тест Дарбина-Уотсона
|
Тест Голдфелда-Квандта
|
t-критерий Стьюдента
|
| 3407,452 |
130,7913 |
DW |
0,383994 |
RSS1
|
617,462 |
Та1
= |
0,10068 |
| 33843,51 |
24,56966 |
dl |
1,35 |
RSS2 |
477,5403 |
Та0
= |
5,32329 |
| 0,000362 |
6,253577 |
du |
1,49 |
GQ |
0,773392 |
Tr
= |
0,10068 |
| 0,010137 |
28 |
4-du |
2,51 |
GQ-1
|
1,293005 |
Tkp
= |
2,04841 |
| 0,396429 |
1095,002 |
4-dl |
2,65 |
Fкр
|
2,403447 |
| Оценка a
1
и a0
|
F-тест
|
| Знач |
НГ |
ВГ |
F |
0,010137 |
| a1
|
3407,452 |
-65710,2 |
72525,12 |
Fкрит |
3,340386 |
| a0
|
130,7913 |
80,37857 |
181,2041 |
| Средняя ошибка аппроксимации
|
3,4% |
| Эластичность
|
1,85% |
Тест Дарбина-Уотсона.
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
Тест Голдфелда-Квандта
· GQ, GQ-1
<Fкр
– гомоскедастичность.
t-критерий Стьюдента
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
F-тест
· , следовательно модель не является качественной.
Средняя ошибка аппроксимации
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 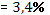 - допустимая ошибка. - допустимая ошибка.
Эластичность
· Расчет коэффициента средней эластичности 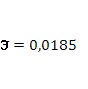 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 1,85%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 1,85%.
 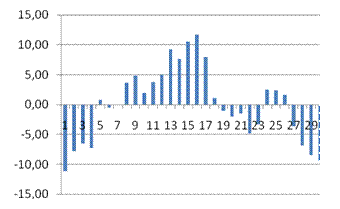
· Проверим адекватность модели используя контролирующую выборку в 40 значений.
| №
|
X
|
Y
|
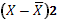 |
Линейн
|
| 1 |
0,000659 |
142,446 |
4,50308E-09 |
4541,709 |
129,8429 |
| 2 |
0,000674 |
139,9897 |
2,65033E-09 |
35134,58 |
25,53489 |
| 3 |
0,000689 |
131,5442 |
1,33288E-09 |
0,000642 |
6,469549 |
| 4 |
0,00073 |
125,6753 |
1,62785E-11 |
0,01671 |
26 |
| 5 |
0,000704 |
137,9529 |
4,83237E-10 |
0,699386 |
1088,232 |
| 6 |
0,000673 |
141,4995 |
2,77759E-09 |
| 7 |
0,000677 |
136,7182 |
2,34714E-09 |
| 8 |
0,000694 |
130,7891 |
1,04362E-09 |
| 9 |
0,000703 |
136,4654 |
5,31824E-10 |
| 10 |
0,000695 |
130,6861 |
9,60026E-10 |
| 11 |
0,000725 |
121,5317 |
1,53662E-12 |
| 12 |
0,000767 |
139,9621 |
1,71214E-09 |
| 13 |
0,00077 |
141,2744 |
1,98284E-09 |
a0
|
a1
|
σu
|
n
|
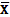 |
n-k
|
| 14 |
0,000762 |
132,6729 |
1,32708E-09 |
129,8429 |
4541,709 |
6,469549 |
28 |
0,00 |
26 |
| 15 |
0,000815 |
144,7476 |
7,98187E-09 |
| 16 |
0,000766 |
140,7004 |
1,61575E-09 |
n
|
X0
|
σu
|
∑(Xi-Xср)2
|
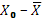 |
q0
|
| 17 |
0,000736 |
131,4057 |
1,02243E-10 |
28 |
0,00 |
6,469549 |
0,0 |
0,00 |
0,038605 |
| 18 |
0,000732 |
124,0129 |
3,18334E-11 |
| 19 |
0,000722 |
132,142 |
1,37258E-11 |
Sy0
|
ỹ0
|
t крит
|
Y0-
|
Y0+
|
Y0
|
| 20 |
0,000728 |
122,725 |
3,72722E-12 |
6,593246 |
133,0949 |
2,055529 |
119,5423 |
146,6476 |
135,3 |
| 21 |
0,000723 |
125,2816 |
1,10827E-11 |
| 22 |
0,000718 |
134,31 |
6,60489E-11 |
| 23 |
0,000735 |
128,4037 |
8,01731E-11 |
| 24 |
0,000746 |
129,6521 |
3,94895E-10 |
a0
|
a1
|
σu
|
n
|
Хср
|
n-k
|
| 25 |
0,00076 |
133,8721 |
1,16714E-09 |
129,8429 |
4541,709 |
6,469549 |
28 |
0,00 |
26 |
| 26 |
0,000749 |
133,4779 |
5,46435E-10 |
| 27 |
0,000736 |
129,4917 |
9,85524E-11 |
n
|
X0
|
σu
|
∑(Xi-Xср)2
|
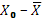 |
q0
|
| 28 |
0,000737 |
128,4874 |
1,23064E-10 |
28 |
0,00 |
6,469549 |
0,0 |
0,00 |
0,040312 |
| 29 |
0,000716 |
135,2644 |
| 30 |
0,000713 |
134,6905 |
Sy0
|
ỹ0
|
t крит
|
Y0-
|
Y0+
|
Y0
|
| Среднее: |
0,000726
|
6,59866 |
133,0832 |
2,055529 |
119,5195 |
146,6469 |
134,7 |
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
130,791 |
y = -0,021 *x + 187,8 |
Та= |
0,10068 |
| а1
= |
3407,45 |
средние квадрат. отклонения
|
Тв= |
5,32329 |
| Дисперсии Х и У
|
Tr= |
0,10068 |
| S2
х= |
1,1E-09 |
Sx= |
3,4E-05 |
Tkp= |
2,04841 |
| S2
у= |
36,5133 |
Sy= |
6,04262 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,01902 |
R2= |
0,00036 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,77339 |
GQ-1
= |
1,293 |
| DW= |
0,38399 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
0,3964 |
Dост= |
39,1072 |
F= |
0,01014 |
Fкр= |
3,34039 |
· Сформирована эконометрическая модель в виде линейного уравнения парной регрессии, связывающая величину цены акции с величиной индекса РТС.
· На основании анализа численного значения коэффициента корреляции 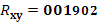 можно сделать вывод о том, что установлена средняя степень связи между стоимостью акции и величиной индекса РТС. можно сделать вывод о том, что установлена средняя степень связи между стоимостью акции и величиной индекса РТС.
· Исходя из коэффициента детерминации 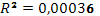 , доля дисперсии цены акции на 0,036% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 0,036% обусловлена дисперсией факторных переменных.
| Результаты исследования: |
| Параметры модели |
Уравнение регрессии |
Проверка значимости коэф-тов |
| а0
= |
2,15768 |
y = -0,021 *x + 187,8 |
Та= |
-3,0832 |
| а1
= |
-753,83 |
средние квадрат. отклонения |
Тв= |
12,156 |
| Дисперсии Х и У |
Tr= |
-3,0832 |
| S2
х= |
1,1E-09 |
Sx= |
3,4E-05 |
Tkp= |
2,04841 |
| S2
у= |
0,00255 |
Sy= |
0,05051 |
| Коэффициент парной корреляции |
Коэффициент детерминации |
| Rxy= |
-0,5034 |
R2= |
0,25346 |
| Проверка значимости уравнения регрессии |
GQ= |
1,17675 |
GQ-1
= |
0,8498 |
| DW= |
1,76399 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
0,0194 |
Dост= |
0,00204 |
F= |
9,50615 |
Fкр= |
3,34039 |
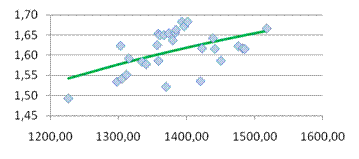 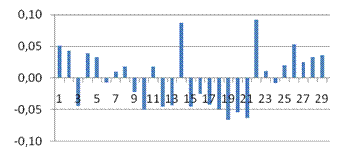
· du
<DW
<4-
du
, следовательно, автокорреляция отсутствует. Случайные возмущения не зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель является качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 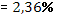 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 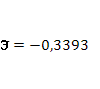 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 34%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 34%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 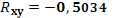 можно сделать вывод о том, что зависимость между стоимостью акции и величиной индекса РТС низкая. можно сделать вывод о том, что зависимость между стоимостью акции и величиной индекса РТС низкая.
· Исходя из коэффициента детерминации 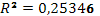 , доля дисперсии цены акции на 25% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 25% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
1688,305 |
y = -0,021 *x + 187,8 |
Та= |
-0,3688 |
| а1
= |
-157237,1 |
средние квадрат. отклонения
|
Тв= |
5,45428 |
| Дисперсии Х и У
|
Tr= |
-0,3688 |
| S2
х= |
1,138E-09 |
Sx= |
3,4E-05 |
Tkp= |
2,04841 |
| S2
у= |
5821,3918 |
Sy= |
76,298 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
-0,069524 |
R2= |
0,00483 |
| Проверка значимости уравнения регрессии
|
GQ= |
1,10709 |
GQ-1
= |
0,90327 |
| DW= |
0,1712681 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
844,1435 |
Dост= |
6207,06 |
F= |
0,136 |
Fкр= |
3,34039 |
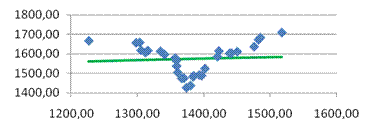 
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель не является качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 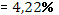 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 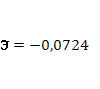 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 7%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 7%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 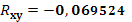 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 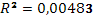 , доля дисперсии цены акции на 0,4% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 0,4% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
45,9459 |
y = -0,021 *x + 187,8 |
Та= |
2,01747 |
| а1
= |
37319,4 |
средние квадрат. отклонения
|
Тв= |
3,42134 |
| Дисперсии Х и У
|
Tr= |
2,01747 |
| S2
х= |
1,1E-09 |
Sx= |
3,4E-05 |
Tkp= |
2,04841 |
| S2
у= |
12,4894 |
Sy= |
3,53403 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,35625 |
R2= |
0,12691 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,5304 |
GQ-1
= |
1,88536 |
| DW= |
0,46241 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
47,5526 |
Dост= |
11,6832 |
F= |
4,07018 |
Fкр= |
3,34039 |
 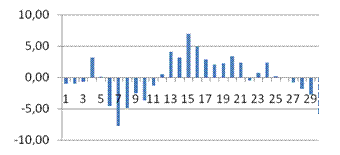
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель является качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 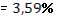 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 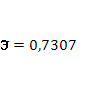 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 73%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 73%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 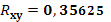 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 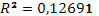 , доля дисперсии цены акции на 12% обусловлена дисперсией факторных переменных. , доля дисперсии цены акции на 12% обусловлена дисперсией факторных переменных.
| Результаты исследования:
|
| Параметры модели
|
Уравнение регрессии
|
Проверка значимости коэф-тов
|
| а0
= |
127,119 |
y = -0,021 *x + 187,8 |
Та= |
1,6001 |
| а1
= |
43679,8 |
средние квадрат. отклонения
|
Тв= |
6,41435 |
| Дисперсии Х и У
|
Tr= |
1,6001 |
| S2
х= |
1,1E-09 |
Sx= |
3,4E-05 |
Tkp= |
2,04841 |
| S2
у= |
25,9185 |
Sy= |
5,09103 |
| Коэффициент парной корреляции
|
Коэффициент детерминации
|
| Rxy= |
0,28945 |
R2= |
0,08378 |
| Проверка значимости уравнения регрессии
|
GQ= |
0,59903 |
GQ-1
= |
1,66937 |
| DW= |
0,47135 |
dl= |
1,35 |
Du= |
1,49 |
| Dфакт= |
65,1431 |
Dост= |
25,4433273 |
F= |
2,56032 |
Fкр= |
3,34039 |
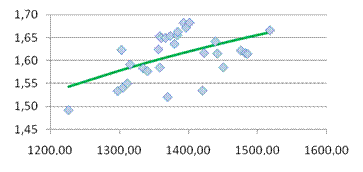 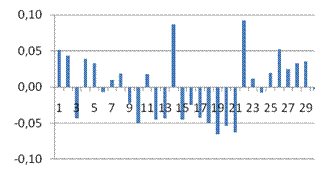
· dl
>DW
, следовательно, автокорреляция присутствует. Случайные возмущения зависят друг от друга.
· GQ, GQ-1
<Fкр
– гомоскедастичность.
· ta1
, < tкр
. ta0
, > tкр
,следовательно, пренебречь константой нельзя.
· , следовательно модель является не качественной.
· Рассчитанная средняя ошибка аппроксимации статистических данных линейным уравнением парной регрессии 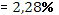 - допустимая ошибка. - допустимая ошибка.
· Расчет коэффициента средней эластичности 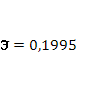 показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 13%. показывает, что при изменении индекса РТС на 1% величина стоимости акции изменится на 13%.
· В процессе интервального прогнозирования установлено, что все значения эндогенной переменной из контрольной выборки попадают в доверительные интервалы, следовательно, оцененная модель может быть признана адекватной.
· На основании анализа численного значения коэффициента корреляции 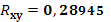 можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет. можно сделать вывод о том, что зависимости между стоимостью акции и величиной индекса РТС нет.
· Исходя из коэффициента детерминации 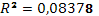 доля дисперсии цены акции на 8% обусловлена дисперсией факторных переменных. доля дисперсии цены акции на 8% обусловлена дисперсией факторных переменных.
Таблица доходности по индексу и каждой акции:
| RTS
|
ОАО РусГидро
|
ОАО ЛУКОЙЛ
|
ОАО Сбербанк России
|
ОАО Татнефть
|
ОАО Газпром
|
| HYDR
|
LKOH
|
SBERG
|
TATN
|
GAZP
|
| -0,02316 |
-0,02977 |
-0,00578 |
-0,02129 |
-0,02399 |
-0,02582 |
| -0,02172 |
-0,01922 |
0,001134 |
-0,00577 |
-0,00929 |
0,005964 |
| -0,05554 |
-0,04075 |
-0,0243 |
-0,05294 |
0,005275 |
-0,031 |
| 0,036959 |
0,009167 |
-0,0074 |
0,042234 |
-0,05705 |
-0,00045 |
| 0,045631 |
0,052011 |
0,006341 |
0,06095 |
0,009038 |
0,02505 |
| -0,00628 |
0,00459 |
-0,00205 |
0,035534 |
-0,00294 |
0,00097 |
| -0,02327 |
-0,00411 |
-0,01027 |
-0,03655 |
-0,02866 |
-0,02228 |
| -0,01315 |
0,000687 |
-0,01097 |
-0,03449 |
-0,00898 |
-0,0041 |
| 0,011401 |
0,01564 |
-0,0086 |
0,014532 |
0,022712 |
0,015264 |
| -0,04104 |
-0,00311 |
-0,01788 |
-0,03092 |
-0,01457 |
-0,0238 |
| -0,05554 |
-0,00829 |
-0,02086 |
-0,02449 |
-0,0084 |
-0,01288 |
| -0,00409 |
-0,05506 |
-0,01995 |
-0,05069 |
-0,0342 |
-0,03994 |
| 0,010625 |
0,010955 |
0,000764 |
0,012177 |
0,013405 |
0,000817 |
| -0,0649 |
-0,03771 |
-0,03311 |
-0,05437 |
-0,02348 |
-0,02854 |
| 0,064146 |
0,032796 |
0,007405 |
0,028375 |
-0,00972 |
0,017403 |
| 0,040873 |
0,072829 |
0,031267 |
0,028465 |
0,030855 |
0,055136 |
| 0,006109 |
-0,00226 |
0,003695 |
0,012099 |
0,05476 |
0,005394 |
| 0,012942 |
0,007955 |
0,00249 |
-0,00549 |
0,016406 |
0,002984 |
| -0,00774 |
-0,00529 |
-0,00218 |
-0,01713 |
0,007106 |
-0,00866 |
| 0,007279 |
0,001028 |
0,024327 |
0,013166 |
-0,00424 |
0,02594 |
| 0,006684 |
0,016359 |
0,039303 |
0,036445 |
0,024221 |
0,037685 |
| -0,02324 |
-0,01988 |
0,018384 |
-0,01806 |
-0,01078 |
-0,01486 |
| -0,01464 |
-0,04359 |
-0,00706 |
-0,02665 |
-0,04235 |
-0,02501 |
| -0,0188 |
0,009118 |
0,000223 |
0,030818 |
0,000788 |
0,00022 |
| 0,014396 |
-0,00525 |
0,005087 |
0,001272 |
0,005773 |
-0,00703 |
| 0,018276 |
0,001187 |
0,015744 |
0,003555 |
0,039333 |
-0,00907 |
| -0,00158 |
0,024864 |
0,021432 |
0,012691 |
0,023929 |
-0,00344 |
| 0,029319 |
0,029 |
0,006408 |
0,012697 |
0,010785 |
0,009692 |
| 0,003623 |
0,006634 |
0,015313 |
0,036529 |
0,006689 |
0,002441 |
| Средие:
|
-0,00229 |
0,000708 |
0,000996 |
9,26E-05 |
-0,00026 |
-0,00179 |
| ЛИНЕЙН()
|
| HYDR
|
LKOH
|
SBERG
|
TATN
|
GAZP
|
| 0,643994 |
0,002184 |
0,32532 |
0,001742 |
0,763936 |
0,001843 |
0,226605 |
0,000258 |
0,473715 |
-0,00071 |
| 0,122021 |
0,003668 |
0,084956 |
0,002554 |
0,130902 |
0,003935 |
0,148386 |
0,004461 |
0,098893 |
0,002973 |
| 0,507789 |
0,019697 |
0,351947 |
0,013714 |
0,557799 |
0,02113 |
0,079507 |
0,023952 |
0,459413 |
0,015963 |
| 27,8545 |
27 |
14,66327 |
27 |
34,0582 |
27 |
2,332122 |
27 |
22,94572 |
27 |
| 0,010806 |
0,010475 |
0,002758 |
0,005078 |
0,015206 |
0,012055 |
0,001338 |
0,01549 |
0,005847 |
0,00688 |
 |
0,0007082
|
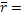 |
0,0009962
|
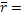 |
9,2E-05
|
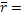 |
-0,00026
|
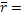 |
-0,00179
|
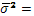 |
0,000388
|
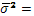 |
0,000283
|
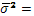 |
0,000971
|
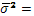 |
0,000620
|
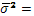 |
0,000456
|
Ковариационная матрица:
| HYDR
|
LKOH
|
SBERG
|
TATN
|
GAZP
|
| HYDR
|
0,000388
|
0,000188 |
0,000442 |
0,000131 |
0,000274 |
| LKOH
|
0,000188 |
0,000283
|
0,000223 |
0,000066 |
0,000138 |
| SBERG
|
0,000442 |
0,000223 |
0,000971
|
0,000156 |
0,000325 |
| TATN
|
0,000131 |
0,000066 |
0,000156 |
0,000620
|
0,000096 |
| GAZP
|
0,000274 |
0,000138 |
0,000325 |
0,000096 |
0,000456
|
Потенциальные портфели акций:
| №
|
Рисковость
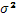 |
HYDR
|
LKOH
|
SBERG
|
TATN
|
GAZP
|
Доходность
r
|
σ
|
| 1 |
0,000 |
0,035 |
0,529 |
0,000 |
0,227 |
0,209 |
0,000 |
0,014 |
| 2 |
0,000 |
0,053 |
0,716 |
0,029 |
0,121 |
0,082 |
0,001 |
0,015 |
| 3 |
0,000 |
0,049 |
0,806 |
0,029 |
0,055 |
0,062 |
0,001 |
0,015 |
| 4 |
0,000 |
0,039 |
0,883 |
0,029 |
0,016 |
0,033 |
0,001 |
0,016 |
| 5 |
0,000 |
0,000 |
1,000 |
0,000 |
0,000 |
0,000 |
0,001 |
0,017 |
Разработка наборов акций в портфелях проводилась при помощи инструмента «Поиск решений» при минимальном значении риска, максимальном значении доходности и при промежуточных значениях риска.
Первый портфель наименее рисковый и наименее доходный из рассмотренных, последний – наиболее доходный и наиболее рисковый из рассмотренных. Риск при выборе набора акций №5 на 41,34% выше, чем при №1, но доходность в восемь с половиной раз выше, так что целесообразно выбрать для вложения средств именно акции «ОАО ЛУКОЙЛ», не взирая на показатель риска σ2
=0,00028.
На основе полученных моделей был проведен прогноз значений средневзвешенной цены акций на 22 июня, 2 и 16 июля.
| Дата
|
22 июн |
2 июл |
16 июл |
| RTS
|
1434,93 |
1316,65 |
1389,92 |
| HYDR
|
Y факт
|
1,77309 |
1,49833 |
1,57027 |
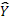 лин лин
|
1,63111 |
1,58626 |
1,61404 |
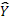 степ степ
|
1,63148 |
1,58459 |
1,61394 |
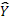 пок пок
|
1,63081 |
1,58519 |
1,61330 |
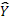 гип гип
|
1,63233 |
1,58514 |
1,61532 |
| LKOH
|
Y
|
1685,25 |
1567,26 |
1609,90 |
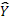 лин лин
|
1612,62 |
1527,08 |
1580,07 |
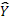 степ степ
|
1578,11 |
1565,48 |
1573,42 |
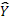 пок пок
|
1579,56 |
1563,66 |
1573,49 |
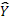 гип гип
|
1578,73 |
1568,88 |
1575,18 |
| SBERG
|
Y
|
82,5370 |
72,7674 |
80,5776 |
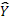 лин лин
|
75,4890 |
69,9581 |
73,3843 |
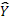 степ степ
|
71,9416 |
74,1450 |
72,7501 |
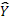 пок пок
|
71,9835 |
74,1012 |
72,7821 |
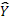 гип гип
|
71,9537 |
74,2901 |
72,7959 |
| TATN
|
Y
|
144,85 |
138,42 |
144,76 |
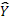 лин лин
|
136,33 |
129,49 |
133,73 |
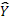 степ степ
|
133,17 |
133,07 |
133,13 |
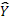 пок пок
|
133,286 |
132,93 |
133,15 |
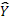 гип гип
|
133,166 |
133,38 |
133,24 |
| GAZP
|
Y
|
160,15 |
146,07 |
157,17 |
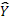 лин лин
|
162,24 |
154,55 |
159,32 |
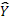 степ степ
|
157,571 |
160,12 |
158,51 |
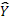 пок пок
|
157,633 |
160,05 |
158,55 |
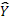 гип гип
|
157,559 |
160,29 |
158,55 |
По визуальной оценке прогноз достаточно неточен и отражает лишь прямую/обратную зависимость показателей от индекса РТС с большой погрешностью. Также проблематично определить модель, лучшим образом подходящую для прогнозных целей.
После проведенной работы затруднительно определить наиболее удачную модель для прогноза: все модели имеют массу недостатков.
Для компании «ОАО РусГидро» все модели подходят лучшим образом, чем для остальных организаций, но лишь из-за специфики начальных данных (более низкая цена за акцию, меньший разброс).
Сложности анализа, скорее всего, связаны с неверным выбором экзогенных переменных: индекс РТС сам зависит от многих компаний, в том числе и от рассматриваемых – а также с очень широким спектром определяющих факторов, влияющих на цены акций (в том числе день недели, сезон, фундаментальные факторы).
Модели были получены на основе данных за полтора месяца, поэтому не могут отражать долгосрочных тенденций.
Июню и июлю 2010 года на фондовых рынках была присуща ситуация неопределённости, подверженности колебаний моментным настроениям, что вообще затрудняло всяческий анализ и прогноз ситуации.
Таким образом, в ходе работы по моделированию средневзвешенной цены на акции пяти компаний было доказано, что при данной выборке и при данном подходе невозможно адекватно оценить ситуацию и правильно её спрогнозировать.
1. Бывшев В.А, Введение в эконометрию: Учебное пособие. Ч. 2. – М.: Финансовая академия, 2003
2. Бывшев В.А. Эконометрика: учеб. пособие. – М.: Финансы и статистика, 2008
3. Фондовая биржа РТС [http://www.rts.ru]
|