МЕТОД ДИНАМІЧНОГО ПРОГРАМУВАННЯ
1 Принцип оптимальності
Оптимальне керування в будь-який момент часу не залежить від передісторії процесу і визначається тільки станом системи в поточний момент і метою керування. Якщо в якийсь період часу керування було неоптимальним, то наслідки цього в майбутньому виправити вже не можна. Під метою керування розуміються вимоги, яким повинна задовольняти керована система, наприклад, це може бути приведення системи в заданий стан або забезпечення певних умов руху протягом заданого періоду часу.
Отже, принцип оптимальності характеризує наступний за заданим станом рух системи, але він може не мати місця для траєкторії, що передує цьому стану.
2 Метод динамічного програмування
Розглянемо застосування методу динамічного програмування до розв’язання неперервних задач оптимального керування. У цьому випадку треба виконати дискретизацію початкової задачі, тобто початкову задачу потрібно замінити близькою їй дискретною задачею. Розглянемо динамічну систему, закон руху якої описується автономним диференціальним рівнянням
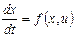 ,(1) ,(1)
де 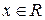 , , 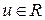 – кусково-неперервні функції. – кусково-неперервні функції.
Припустимо, що початковий стан системи 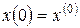 заданий, а на керування накладено обмеження заданий, а на керування накладено обмеження 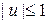 . Вважатимемо, що час руху . Вважатимемо, що час руху 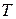 фіксований. Цільовий функціонал задачі в цьому випадку матиме вигляд: фіксований. Цільовий функціонал задачі в цьому випадку матиме вигляд:
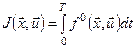 .(2) .(2)
Для дискретизації неперервної задачі (1) – (2) розіб'ємо відрізок 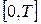 на на 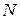 інтервалів довжиною інтервалів довжиною
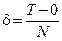
кожний, де 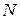 – натуральне число . Значення функцій – натуральне число . Значення функцій 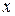 і і 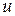 будемо далі визначати лише в дискретні моменти часу будемо далі визначати лише в дискретні моменти часу 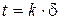 , де , де 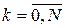 . Для цього введемо позначення . Для цього введемо позначення 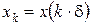 , , 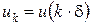 , і замінимо диференціальне рівняння (1) різницевим, апроксимуючи першу похідну значеннями в дискретні моменти часу: , і замінимо диференціальне рівняння (1) різницевим, апроксимуючи першу похідну значеннями в дискретні моменти часу:
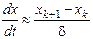 . .
З останнього співвідношення випливає, що
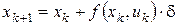 , , 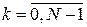 .(3) .(3)
Інтегральному цільовому функціоналу (2) відповідає інтегральна сума
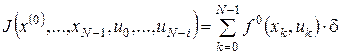 .(4) .(4)
Отже, ми перейшли до дискретної задачі, у якій потрібно знайти такі керування 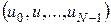 , що задовольняють обмеженню , що задовольняють обмеженню 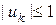 , , 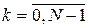 , і мінімізують функціонал (4) за початкових умов , і мінімізують функціонал (4) за початкових умов 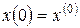 . Очевидно, що результати розв’язання цієї задачі будуть тим точніше апроксимувати початкову неперервну задачу, чим більше . Очевидно, що результати розв’язання цієї задачі будуть тим точніше апроксимувати початкову неперервну задачу, чим більше 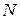 . .
Розглянемо співвідношення
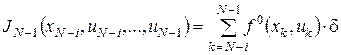 , , 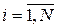 , ,
де 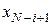 , …, , …, 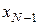 визначаються за рекурентними формулами (3), і позначимо визначаються за рекурентними формулами (3), і позначимо
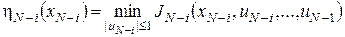 . .
Величина 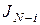 – це частина інтегральної суми (4), що відноситься до моментів часу – це частина інтегральної суми (4), що відноситься до моментів часу
Реклама

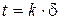 , ,
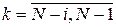
і залежить від стану 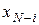 системи в момент часу системи в момент часу
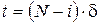 . .
Відповідно до принципу оптимальності, керування 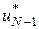 на останньому етапі треба обирати так, щоб на останньому етапі треба обирати так, щоб
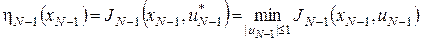 . .
Далі будемо розглядати лише задачі, у яких зазначений мінімум досягається в єдиній точці.
На наступному етапі визначимо керування 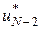 , для якого , для якого
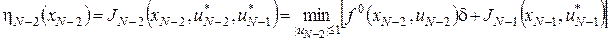 , ,
де
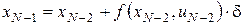 , ,
а
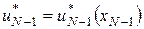
– керування, що залежить від стану, у якому перебуває система. Отже, на передостанньому відрізку часу знайдене оптимальне керування як функція від стану 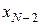 , в якому перебуватиме система на момент часу , в якому перебуватиме система на момент часу
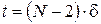 . .
Повторюючи цю процедуру, на 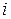 -му етапі потрібно визначити оптимальне керування -му етапі потрібно визначити оптимальне керування 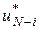 , що задовольняє співвідношенню , що задовольняє співвідношенню
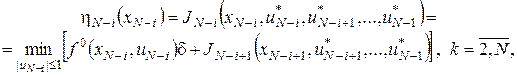 (5) (5)
де
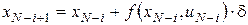
відповідно до (3). Співвідношення (5) називаються рекурентними співвідношеннями Беллмана.
Після того, як на останньому етапі буде знайдено значення 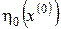 і оптимальне керування і оптимальне керування 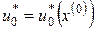 , то за відомим значенням , то за відомим значенням 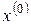 можна визначити послідовно можна визначити послідовно 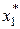 , , 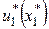 , …, , …, 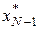 , , 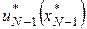 , , 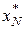 . При цьому значення . При цьому значення 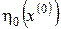 відповідає мінімальному значенню функціонала (4). відповідає мінімальному значенню функціонала (4).
Наведений алгоритм розв’язання задачі оптимального керування методом динамічного програмування можна перенести на загальний випадок задачі керування з векторним законом руху (1), тобто якщо 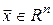 , , 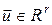 . .
3 Принцип оптимальності для задачі оптимального керування з фіксованим часом і вільним правим кінцем
Розглянемо автономну систему
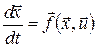 ,(6) ,(6)
з цільовим функціоналом
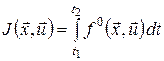 ,(7) ,(7)
у якому початковий і кінцевий моменти часу 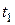 і і 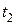 задані, і заданий початковий стан задані, і заданий початковий стан 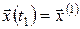 . .
Починаючи з будь-якого моменту часу 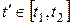 , відрізок оптимальної траєкторії , відрізок оптимальної траєкторії 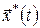 , , 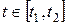 від точки від точки 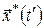 до точки до точки 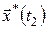 також є оптимальною траєкторією. також є оптимальною траєкторією.
Відносно початкового відрізка оптимальної траєкторії до точки 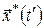 можна стверджувати, що цей відрізок є оптимальною траєкторією, лише у тому випадку, коли точка можна стверджувати, що цей відрізок є оптимальною траєкторією, лише у тому випадку, коли точка 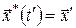 фіксована (наприклад, у багатоточкових задачах керування), тобто коли за умовами припустима траєкторія обов'язково повинна проходити через точку фіксована (наприклад, у багатоточкових задачах керування), тобто коли за умовами припустима траєкторія обов'язково повинна проходити через точку 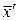 . Якщо ж задана тільки початкова точка . Якщо ж задана тільки початкова точка 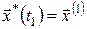 , то відрізок оптимальної траєкторії може і не бути оптимальною траєкторією, тобто може не доставляти оптимальне значення функціоналу (7). , то відрізок оптимальної траєкторії може і не бути оптимальною траєкторією, тобто може не доставляти оптимальне значення функціоналу (7).
4 Рівняння Беллмана в задачі з фіксованим часом і вільним правим кінцем
Розглянемо систему з законом руху (6) і критерієм оптимальності (2). Початковий стан системи заданий:
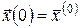 ,(8) ,(8)
час руху 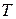 відомий, а кінцевий стан відомий, а кінцевий стан 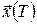 – невідомий. Побудована таким чином задача – це задача з фіксованим часом і вільним правим кінцем. – невідомий. Побудована таким чином задача – це задача з фіксованим часом і вільним правим кінцем.
Позначимо через 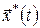 , ,  оптимальну траєкторію, яка відповідає оптимальному керуванню оптимальну траєкторію, яка відповідає оптимальному керуванню 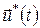 . Зафіксуємо деякий момент часу . Зафіксуємо деякий момент часу 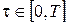 і відповідну йому точку і відповідну йому точку 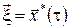 на оптимальній траєкторії. Відповідно до принципу оптимальності, відрізок траєкторії на оптимальній траєкторії. Відповідно до принципу оптимальності, відрізок траєкторії 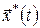 від точки від точки 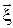 до точки до точки 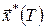 є оптимальною траєкторією і надає найменшого значення функціоналу є оптимальною траєкторією і надає найменшого значення функціоналу
Реклама

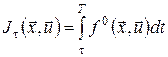
серед всіх припустимих процесів 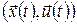 на відрізку часу на відрізку часу 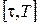 з початковим станом з початковим станом 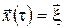 , тобто , тобто
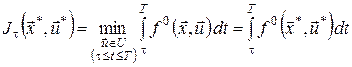 . .
Припустимо, що для будь-якої точки 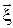 фазового простору фазового простору 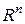 і будь-якого моменту часу і будь-якого моменту часу 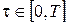 існує оптимальна траєкторія з початковою умовою існує оптимальна траєкторія з початковою умовою 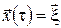 , яка надає найменшого значення функціоналу , яка надає найменшого значення функціоналу 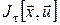 . Позначимо це мінімальне значення через . Позначимо це мінімальне значення через
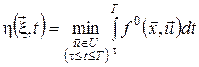 . .
Функція 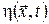 , що задана у всіх точках , що задана у всіх точках 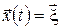 , простору , простору 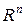 , , 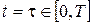 , називається функцією Беллмана. , називається функцією Беллмана.
Припустимо, що 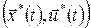 , , 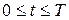 , – оптимальний процес і оптимальна траєкторія , – оптимальний процес і оптимальна траєкторія 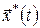 задовольняє початковій умові задовольняє початковій умові 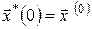 . Тоді . Тоді
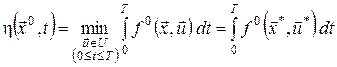
визначає цільовий функціонал (2) початкової задачі.
Розглянемо приріст 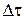 і відповідний йому момент часу і відповідний йому момент часу 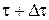 . Очевидно, що останнє співвідношення можна переписати так: . Очевидно, що останнє співвідношення можна переписати так:
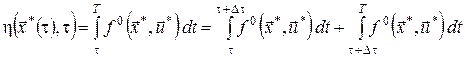 .(9) .(9)
Відповідно до принципу оптимальності, відрізок оптимальної траєкторії від точки 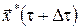 до точки до точки 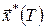 також є оптимальною траєкторією, тобто також є оптимальною траєкторією, тобто
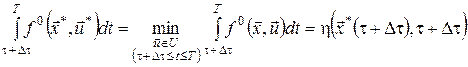 , ,
тому співвідношення (9) можна переписати у вигляді
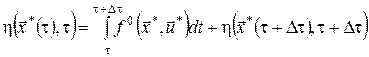 .(10) .(10)
Очевидно, що другий доданок в (10) залежить від стану системи 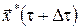 (оскільки оптимальне значення функціонала (оскільки оптимальне значення функціонала 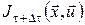 залежить від початкового стану системи залежить від початкового стану системи 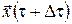 і для кожного початкового стану і для кожного початкового стану 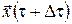 оптимальне значення функціонала оптимальне значення функціонала 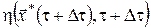 різне). У цей стан різне). У цей стан 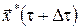 , у свою чергу, система попадає під дією керування , у свою чергу, система попадає під дією керування 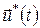 , яке діє на інтервалі часу , яке діє на інтервалі часу 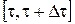 . Отже, значення . Отже, значення 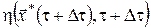 залежатиме від вибору керування на відрізку залежатиме від вибору керування на відрізку 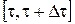 . .
Дійсно, розглянемо різні припустимі керування 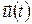 на відрізку на відрізку 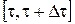 . Їм відповідатиме набір траєкторій . Їм відповідатиме набір траєкторій 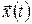 , що виходять із точки , що виходять із точки 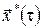 , яка лежить на оптимальній траєкторії , яка лежить на оптимальній траєкторії 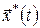 . На кожній траєкторії із цього набору фазова точка в момент часу . На кожній траєкторії із цього набору фазова точка в момент часу 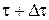 попаде в деякий стан попаде в деякий стан 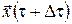 . .
Виберемо керування 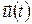 на відрізку на відрізку 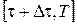 так, щоб траєкторія так, щоб траєкторія 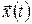 на цьому відрізку була оптимальною. Це оптимальне керування в загальному випадку різне для кожної траєкторії пучка. Очевидно, що вибираючи одне – оптимальне – серед всіх можливих керувань на цьому відрізку була оптимальною. Це оптимальне керування в загальному випадку різне для кожної траєкторії пучка. Очевидно, що вибираючи одне – оптимальне – серед всіх можливих керувань 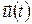 , , 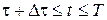 для кожної із траєкторій для кожної із траєкторій 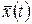 , ми фіксуємо подальший стан кожної із них і при цьому одержуємо мінімальне значення функціонала , ми фіксуємо подальший стан кожної із них і при цьому одержуємо мінімальне значення функціонала
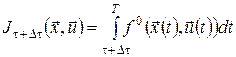 , ,
яке дорівнює
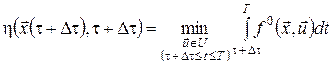 . .
Очевидно, що це значення залежить від стану 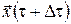 . А оскільки, як було встановлено раніше, стан . А оскільки, як було встановлено раніше, стан 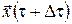 залежав від вибору керування залежав від вибору керування 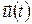 на відрізку на відрізку 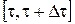 , то й значення , то й значення 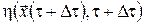 також залежатиме від того, яким було обрано керування також залежатиме від того, яким було обрано керування 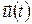 , , 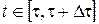 . .
Розглянемо значення функціонала 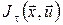 на траєкторіях з набору, побудованого вище при на траєкторіях з набору, побудованого вище при 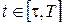 . Оскільки відрізок кожної траєкторії . Оскільки відрізок кожної траєкторії 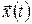 від точки від точки 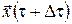 до точки до точки 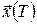 є оптимальним відповідно до принципу максимуму, то значення функціонала дорівнює є оптимальним відповідно до принципу максимуму, то значення функціонала дорівнює
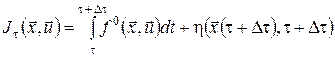 .(11) .(11)
Ясно, що останнє співвідношення різне для кожної з траєкторій 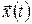 і відповідного цій траєкторії керування і відповідного цій траєкторії керування 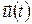 на відрізку на відрізку 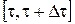 . Виберемо серед всіх значень . Виберемо серед всіх значень 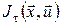 мінімальне. Оскільки обидва доданки в (11) залежать тільки від вибору керування мінімальне. Оскільки обидва доданки в (11) залежать тільки від вибору керування 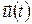 на інтервалі на інтервалі 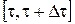 , то і мінімальне значення (11) залежатиме тільки від вибору керування на цьому інтервалі, тобто , то і мінімальне значення (11) залежатиме тільки від вибору керування на цьому інтервалі, тобто
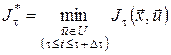 . .
Побудований набір траєкторій є підмножиною більш широкої множини всіх припустимих функцій, на яких шукається найменше значення функціонала 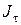 . Тому в загальному випадку має місце нерівність . Тому в загальному випадку має місце нерівність
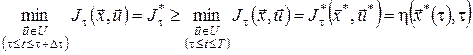 .(12) .(12)
Але оскільки оптимальна траєкторія 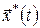 належить до побудованого набору траєкторій, то в співвідношенні (12) насправді має місце рівність, тобто належить до побудованого набору траєкторій, то в співвідношенні (12) насправді має місце рівність, тобто
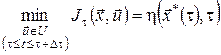 . .
Звідси з урахуванням (11) одержимо
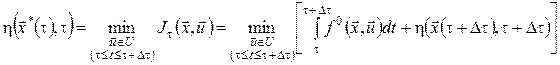 , (13) , (13)
тобто оптимізація процесу проводиться тільки для 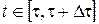 , тому що для , тому що для 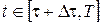 траєкторія вже оптимальна. траєкторія вже оптимальна.
Розглянемо поведінку останнього співвідношення при 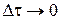 , тобто коли інтервал , тобто коли інтервал 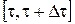 , на якому шукається оптимальне керування, звужується до точки. Відповідно до закону руху , на якому шукається оптимальне керування, звужується до точки. Відповідно до закону руху
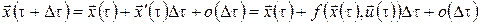 . .
Вважатимемо, що функція Беллмана 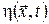 неперервно диференційована по всіх своїх аргументах. Тоді неперервно диференційована по всіх своїх аргументах. Тоді
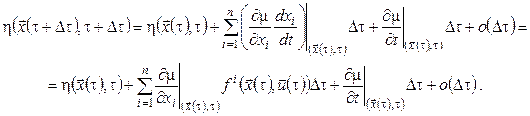 (14) (14)
Позначатимемо далі
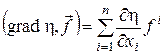 . .
Співвідношення (14) з урахуванням цього позначення набуде вигляду
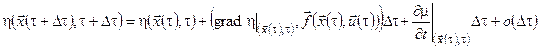 . .
Використовуючи останнє співвідношення, рівність (13) можна подати у вигляді
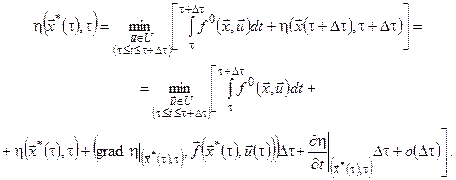 (15) (15)
Оскільки функції 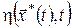 і і 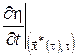 у правій частині (15) не залежать від у правій частині (15) не залежать від 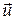 , їх можна винести за знак мінімуму. Після скорочень одержимо , їх можна винести за знак мінімуму. Після скорочень одержимо
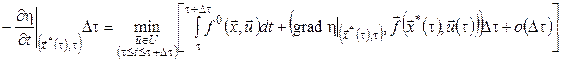 . .
Припустимо, що функція 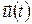 є неперервною на відрізку є неперервною на відрізку 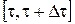 . Розділивши останнє співвідношення на . Розділивши останнє співвідношення на 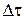 , при , при 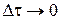 одержимо одержимо
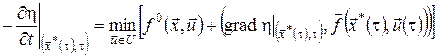 .(16) .(16)
Останнє співвідношення називається рівнянням Беллмана. Воно є аналогом рекурентних рівнянь Беллмана дискретної задачі оптимального керування для випадку неперервної системи.
Замінивши 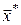 на на 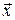 , де , де 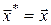 – оптимальна траєкторія, одержимо з (16) – оптимальна траєкторія, одержимо з (16)
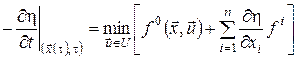 .(17) .(17)
До рівняння Беллмана додаються крайові умови, що випливають безпосередньо з визначення функції Беллмана:
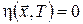 .(18) .(18)
Рівняння Беллмана – це диференціальне рівняння в частинних похідних відносно функції 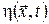 . Але це рівняння не є лінійним через наявність у (17) операції мінімізації. Фактично це означає підстановку в рівняння такого . Але це рівняння не є лінійним через наявність у (17) операції мінімізації. Фактично це означає підстановку в рівняння такого 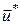 , на якому досягається мінімум і яке змінюється в залежності від значень , на якому досягається мінімум і яке змінюється в залежності від значень 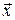 і і 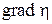 . .
5 Рівняння Беллмана в задачі з фіксованими кінцями та вільним часом
Додамо до задачі (2), (6), (9) умову закріплення правого кінця траєкторії 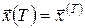 , де , де 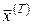 – задано, а – задано, а 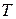 – невідомо. У цьому випадку функція Беллмана залежатиме тільки від поточного стану системи. Дійсно, згідно з визначенням функції Беллмана – невідомо. У цьому випадку функція Беллмана залежатиме тільки від поточного стану системи. Дійсно, згідно з визначенням функції Беллмана
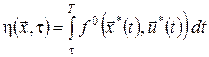 . .
Якщо підінтегральна функція не залежить від 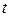 , то значення інтеграла , то значення інтеграла 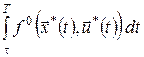 при фіксованих при фіксованих 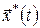 і і 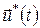 залежить тільки від довжини інтервалу інтегрування залежить тільки від довжини інтервалу інтегрування 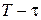 , який можна визначити з автономної системи (6), якщо відомі точки , який можна визначити з автономної системи (6), якщо відомі точки 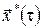 і і 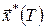 фазової траєкторії. Тому різниця фазової траєкторії. Тому різниця 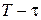 – це функція від аргументів – це функція від аргументів 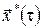 і і 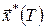 , а , а 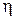 не залежить явно від не залежить явно від 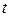 . У цьому випадку . У цьому випадку 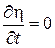 і рівняння Беллмана для задачі із закріпленими кінцями набуває вигляду і рівняння Беллмана для задачі із закріпленими кінцями набуває вигляду
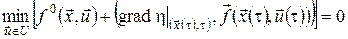 . .
6 Рівняння Беллмана в задачі швидкодії
Розглянемо задачу оптимальної швидкодії з фіксованими кінцями і вільним часом, закон руху якої має вигляд (6) і задані початковий стан 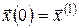 та кінцевий стан та кінцевий стан 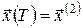 . Час . Час 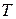 невідомий і його потрібно знайти з умови мінімізації цільового функціонала невідомий і його потрібно знайти з умови мінімізації цільового функціонала
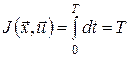 . .
У задачі з фіксованими кінцями і вільним часом функція Беллмана залежить тільки від поточного стану системи і не залежить від моменту, починаючи з якого розглядається її еволюція (доведення аналогічно п. 5), тобто 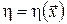 . .
Вважатимемо, що функція 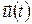 неперервна на будь-якому відрізку неперервна на будь-якому відрізку 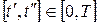 і для будь-якої точки фазового простору і для будь-якої точки фазового простору 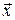 і будь-якого моменту часу і будь-якого моменту часу 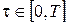 існує оптимальна траєкторія, а функція існує оптимальна траєкторія, а функція 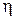 неперервно диференційована за своїми аргументами. Тоді необхідна умова оптимальності у вигляді рівняння Беллмана (17), (18) для даної задачі матиме вигляд: неперервно диференційована за своїми аргументами. Тоді необхідна умова оптимальності у вигляді рівняння Беллмана (17), (18) для даної задачі матиме вигляд:
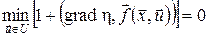 , ,
або
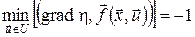
за заданих крайових умов 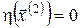 . .
Очевидно, що якщо процес 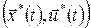 – оптимальний, то, будучи підставленим у рівняння Беллмана, він дасть тотожність – оптимальний, то, будучи підставленим у рівняння Беллмана, він дасть тотожність
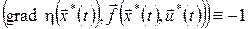 . .
Зауваження. Оскільки функція Беллмана 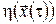 дорівнює мінімальному значенню цільового функціонала, що характеризує перехід системи в кінцевий стан зі стану дорівнює мінімальному значенню цільового функціонала, що характеризує перехід системи в кінцевий стан зі стану 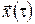 , то в задачі оптимальної швидкодії ця функція показує оптимальний час переходу , то в задачі оптимальної швидкодії ця функція показує оптимальний час переходу 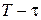 зі стану зі стану 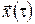 у фіксований стан у фіксований стан 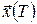 . .
7 Зв'язок методу динамічного програмування із принципом максимуму
Розглянемо задачу оптимального керування з фіксованими кінцями та вільним часом (6) з цільовим функціоналом 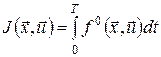 , і крайовими умовами , і крайовими умовами 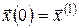 , , 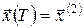 . Вважатимемо, що час . Вважатимемо, що час 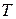 невідомий. невідомий.
Оптимальне керування будемо вибирати серед кусково-неперервних вектор-функцій 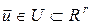 . За принципом динамічного програмування для оптимального процесу . За принципом динамічного програмування для оптимального процесу 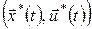 існує такий розв’язок існує такий розв’язок 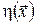 рівняння Беллмана рівняння Беллмана
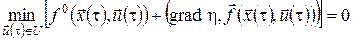 ,(19) ,(19)
що 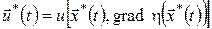 – значення, на якому досягається мінімум у лівій частині рівняння (19). – значення, на якому досягається мінімум у лівій частині рівняння (19).
Доведемо, що з рівняння (19) випливає існування деякого вектора 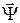 , який задовольняє співвідношенням принципу максимуму. Нехай , який задовольняє співвідношенням принципу максимуму. Нехай 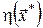 – функція Беллмана, що відповідає оптимальному процесу – функція Беллмана, що відповідає оптимальному процесу 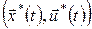 . Розглянемо нову змінну . Розглянемо нову змінну
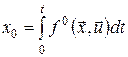
і нову функцію
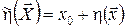 , ,
де 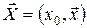 . .
Використовуючи ці позначення, перетворимо рівняння Беллмана. Очевидно, що
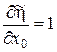 , , 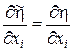 , , 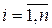 , ,
тому
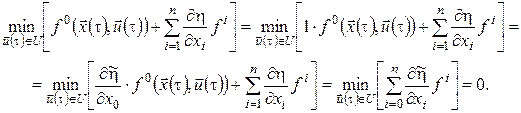
Оскільки 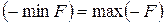 , то останнє співвідношення можна привести до вигляду: , то останнє співвідношення можна привести до вигляду:
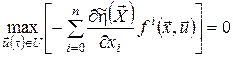 .(20) .(20)
Позначимо
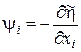 , , 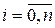 . .
Тоді формула (20) стає аналогом функції Понтрягіна
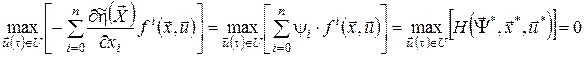 , ,
де 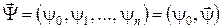 . .
Це означає, що на оптимальному процесі 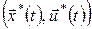 функція Понтрягіна набуває максимального значення, рівного 0. Очевидно, що функція Понтрягіна не залежить від функція Понтрягіна набуває максимального значення, рівного 0. Очевидно, що функція Понтрягіна не залежить від 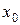 , тому що , тому що 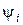 і і 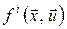 , , 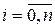 не залежать від не залежать від 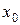 . .
Доведемо, що спряжені змінні 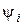 задовольняють спряженій системі задовольняють спряженій системі
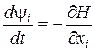 , , 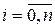 .(21) .(21)
Для цього припустимо, що функція Беллмана 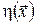 має неперервні частинні похідні другого порядку. Позначимо має неперервні частинні похідні другого порядку. Позначимо
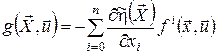 .(22) .(22)
Оскільки оптимальне керування 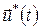 однозначно визначає оптимальну траєкторію однозначно визначає оптимальну траєкторію 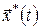 , то функція , то функція 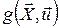 досягає на кожному фіксованому досягає на кожному фіксованому 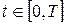 по змінній по змінній 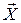 максимального значення, рівного 0, у точці максимального значення, рівного 0, у точці 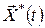 , що відповідає оптимальному керуванню , що відповідає оптимальному керуванню 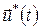 в цій точці. У цьому випадку для функції в цій точці. У цьому випадку для функції 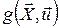 в будь-який момент часу для процесу в будь-який момент часу для процесу 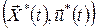 буде виконана умова буде виконана умова
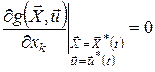 , , 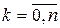 , , 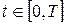 .(23) .(23)
Продиференціюємо співвідношення (22):
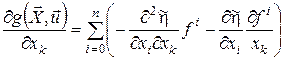 , , 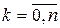 . .
Тоді відповідно до (23) для оптимального процесу дістанемо
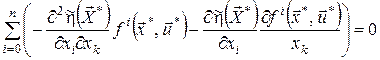 , , 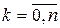 .(24) .(24)
Оскільки
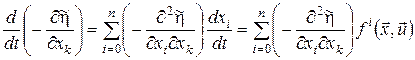 , ,
то співвідношення (24) можна переписати у вигляді:
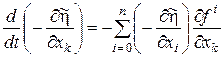 , ,
або, з урахуванням позначень (21),
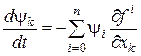 , , 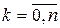 . .
Оскільки 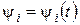 , то , то
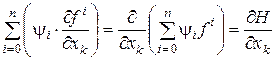 , ,
а це, у свою чергу означає, що
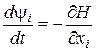 , , 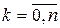 . .
Отже, встановлено теоретичний зв'язок принципу максимуму з методом динамічного програмування. Але на практиці виконати подібну операцію не завжди можливо. Так наприклад, рівняння (21) було отримано в припущенні, що функція Беллмана 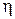 має неперервні похідні другого порядку, що не завжди виконується. має неперервні похідні другого порядку, що не завжди виконується.
Обидва методи придатні для задач, у яких відсутні обмеження на керування, і всі функції гладкі. Кожний з цих методів може бути застосований там, де не працює інший. Рівняння Беллмана вимагає більше припущень для застосування (неперервність і диференційованість функцій), а принцип максимуму складніше використовувати для розв’язання дискретних задач.
|