Контрольная работа по дисциплине «Математика»
для студентов заочного отделения
1. Найти пределы функций:
а) 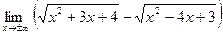 =; =; 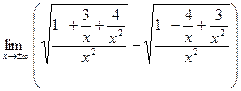 = =
= 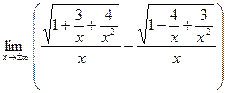 = = 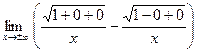 = =
= 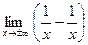 = = 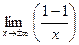 = = 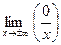 = 0; = 0;
б) 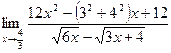 = = 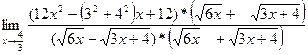 = =
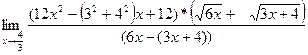 = =
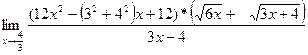 = =
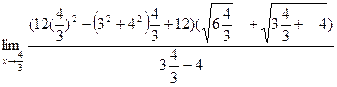 = = 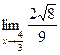 = = 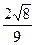 =.6290; =.6290;
в) 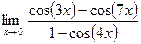 = = 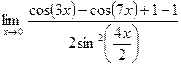 = =
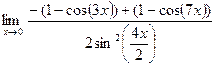 = = 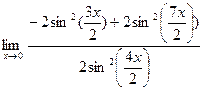 = = 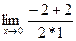 = 0; = 0;
г) 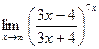 = =  = = 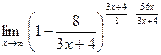 = = 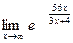 = =
= ln 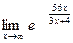 = = 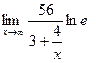 = ln e* = ln e*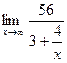 = 1*56/3 = 18.667; = 1*56/3 = 18.667;
д) 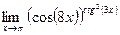 ; ; 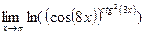 = = 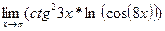 = =
= 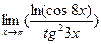 = = 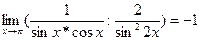 ; ;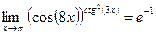 ; ;
е) 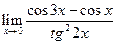 = = 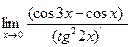 = = 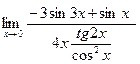 = =
= 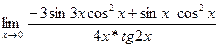 = = 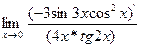 + + 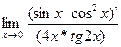 = =
= 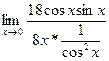 - - 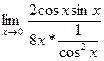 = = 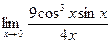 - - 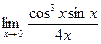 = =
= 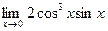 = 2. = 2.
2. Найти производные 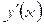 функций: функций:
а) 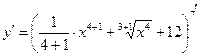 = = 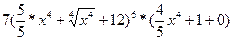 = =
= 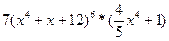 ; ;
б) 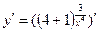 = = 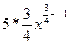 = = 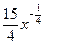 = =  ; ;
в) 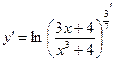 = = 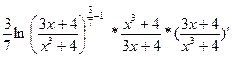 = =
= 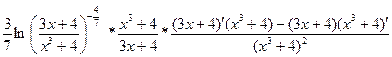 = =
= 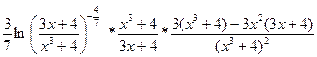 = =
= 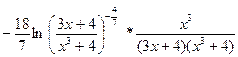 ; ;
г) 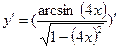 = =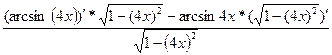 = =
= 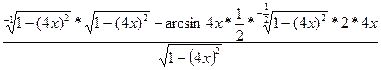 = =
= 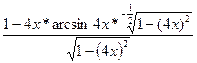 = = 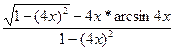 ; ;
д) 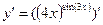 = = 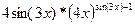 ; ;
е) 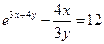 ; ; 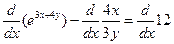 ; ;
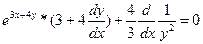 ; ;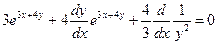
ж) 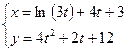 ; ;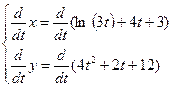 ; ; 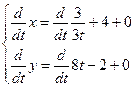 ; ;
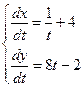 ; ; 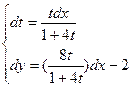 ; ;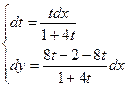 ; ; 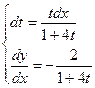 ; ;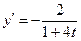 ; ;
з) 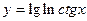 . .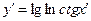 = = 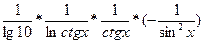 = =
= 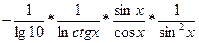 = = 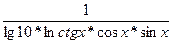 ; ;
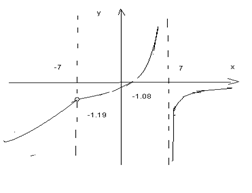
3. С помощью методов дифференциального исчисления построить график функции
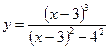 . .
1 Знаменатель положительный не для всех значений Х, область определения функции имеет точку разрыва. 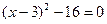 отсюда IхI=7 или точки разрыва х = -7 и х=7. отсюда IхI=7 или точки разрыва х = -7 и х=7.
2. Функция нечетная, следовательно график симметричен относительно центра координат. У(-х) = -У(х). Периодической функция не является.
3. Поскольку область определения вся вещественная ось, вертикальных асимтот график не имеет.
4. Найдем асимптоты при 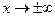 в виде у = kх+b. Имеем: в виде у = kх+b. Имеем:
k =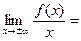 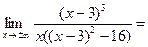 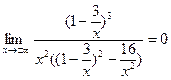
b = 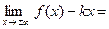 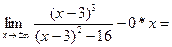 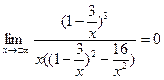
Таким образом при 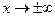 асимптотой служит прямая ОХ оси координат. асимптотой служит прямая ОХ оси координат.
Найдем левый и правый пределы в точках разрыва функции х=-7 и х=+7
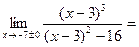 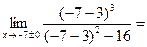 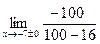 =-1,19, =-1,19,
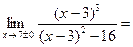 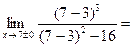 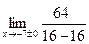 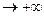 . .
В точке (-7:-1,19) первый разрыв функции, К разрыву функции х=7 функции приближается бесконечно близко.
5. Найдем точки пересечения с осями координат:
Точка (0:3,86) с осью ОУ.
6. Исследуем на возрастание и убывание:
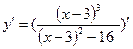 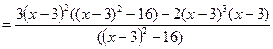 = =
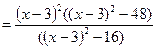 . .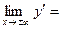 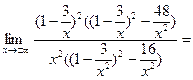 0; 0;
Это говорит о том что функция возрастающая.
Строим график:
4. Найти интегралы при m=3, n=4:
а)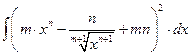 = = 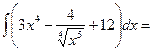 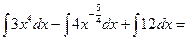
= 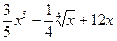 : :
б)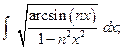 = = 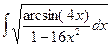 = =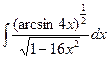 пусть t = arcsin4x, пусть t = arcsin4x,
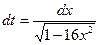 получим получим 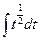 = = 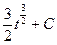 = = 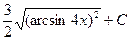 . .
в)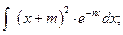 = = 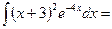 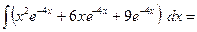
= 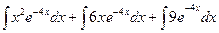 ; ;
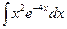 = =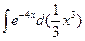 = =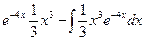 . .
Решаем равенство и получим:
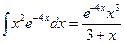 ; ;
аналогично второе слагаемое
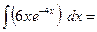 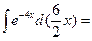 3 3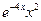 - -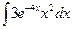 получим получим 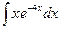 = = 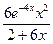
подставим все в последнее равенство
… = 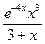 + + 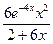 +9 +9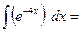 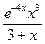 + +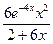 - -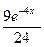 +С. +С.
г)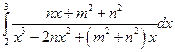 .= .= 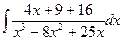 = = 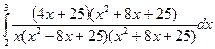 = =
= 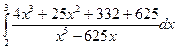 = =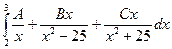 = =
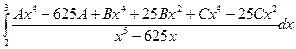 = ….избавившись = ….избавившись
от знаменателя получим
B+C+A=0; 25B=332; -625A=625; 25=25(B-C);
Т.е.: A=1; B= 13.28; C=-12.28;
…= 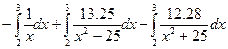 = = = =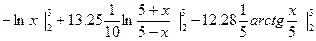 = 2,527766. = 2,527766.
5. Вычислить интегралы или установить их расходимость при m=3, n=4:
а) 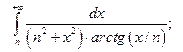 = = 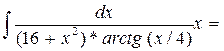 … …
пусть t = arctg(x/4), тогда 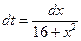 и и 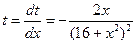 подставим и получим подставим и получим
… = 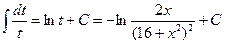 ; ;
б)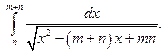 = = 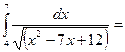 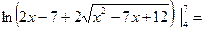
= 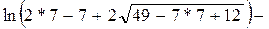 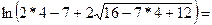 0,6880057. 0,6880057.
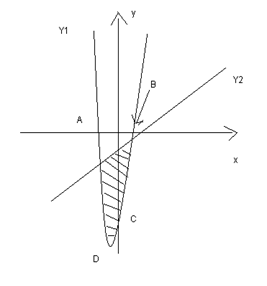
6. Построить схематический чертеж и найти площадь фигуры, ограниченной линиями: 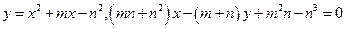 , при m=3, n=4. , при m=3, n=4.
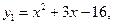 
 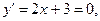 х = -1,5, у = -18,25. х = -1,5, у = -18,25.
точки пересечения с осью ОХ: А(-4,19:0) и В(1,19:0) с осью ОУ – С(0:-16), точка перегиба – D(-1,5:-18,25)
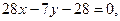 или или 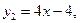
Точки пересечения двух функций:
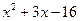 = = 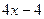 и и 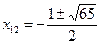 т.е.: т.е.: 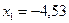 и и 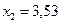 . .
Площадь получиться из выражения
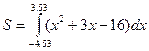 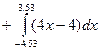 = = 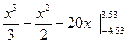 = 49,679. = 49,679.
График выглядит:
7. Найти частные производные 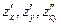 функций при m=3, n=4: функций при m=3, n=4:
Реклама

а)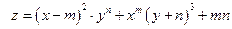 = =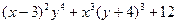 , ,
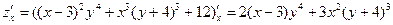 , ,
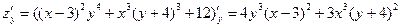 , ,
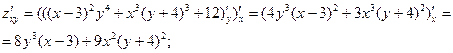
б)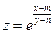 . . 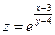 ; ;
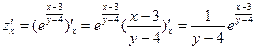 ; ;
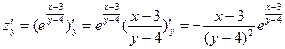
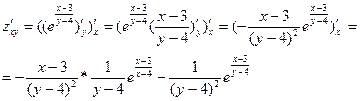
8. Найти дифференциал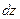 функции: функции: 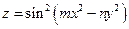 при m=3, n=4. при m=3, n=4.
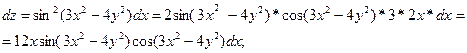
9. Для функции 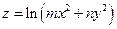 в точке в точке 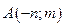 найти градиент и производную по направлению найти градиент и производную по направлению 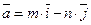 при m=3, n=4. при m=3, n=4.
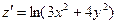 в точке А(-4,3) в точке А(-4,3)
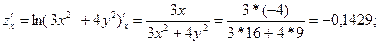
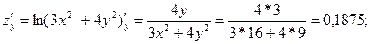
grad(z) = (-0,1429:0,1875);
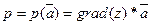 =grad(z)* ( =grad(z)* (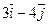 )*cos )*cos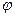 =… =…
cos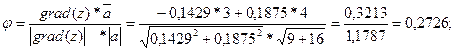
10. Найти наибольшее и наименьшее значения функции при m=3, n=4
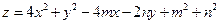
в области, заданной неравенствами:
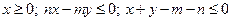 . .
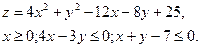
D=AC-B;
A=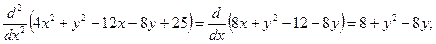
B=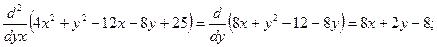
C=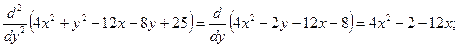
D=AC-B=(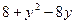 )( )(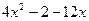 ) - ) - 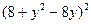 ; ;
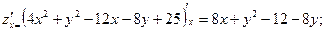
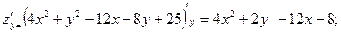
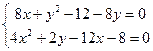 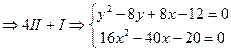
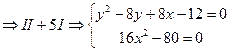 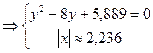
найдем
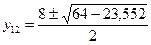 ; ; 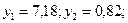
Получим четыре точки: 1) (2,236:7,18), (1,236:0,82), (-2,236:7,18), (-2,236:0,82).
A=8+7,18*7,18-8*7,18=2,11 > 0;
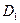 = -114,74 < 0 – нет экстремума функции, = -114,74 < 0 – нет экстремума функции,
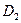 = 45097,12 > 0 – min функции = 45097,12 > 0 – min функции 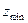 = 12,279; = 12,279;
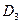 = 1767.38 > 0 - min функции = 1767.38 > 0 - min функции 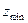 = 65,94; = 65,94;
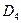 = -160,296 < 0 – нет экстремума функции. = -160,296 < 0 – нет экстремума функции.
11. Изменить порядок интегрирования при m=3, n=4:
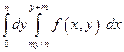 . .
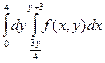 = = 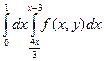 , так как , так как 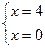 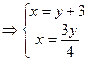 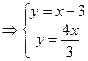
подставляя x = 0 x = 4 в последние уравнения получим
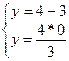 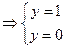 . .
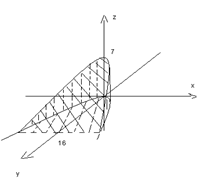
12. Сделать чертеж и найти объем тела, ограниченного поверхностями 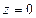 , , 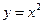 и плоскостью, проходящей через точки и плоскостью, проходящей через точки 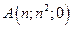 , , 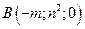 и и 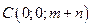 . .
А)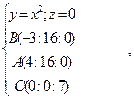 см. рис. см. рис.
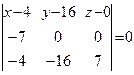
- получим уравнение плоскости, через которую проходят точки А, В и С.
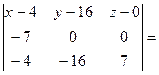 7(х-4)+7*16*(z-0)-(y-16)*4+4(z-0)+49(y-16)+16(x-4)= 7(х-4)+7*16*(z-0)-(y-16)*4+4(z-0)+49(y-16)+16(x-4)=
23x-812+116z-45y=0
Получим пределы интегрирования:
Для z – от 0 до z=7-0,198x+0,388y. Для у – от 0 до у=х^2. Для х – от 0 до х=76,81(объем фигуры разбиваем пополам).
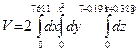 = = 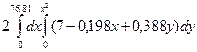 = =
=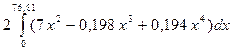 = = 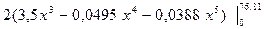 = =
=232,109 куб.ед.,
13. Вычислить при m=3, n=4 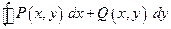 , где , где 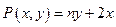 , , 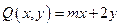 , а контур , а контур 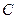 образован линиями образован линиями 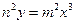 , , 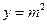 , , 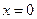 . .
а) непосредственно;
б) по формулам Грина.
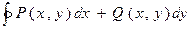 , ,
P(x,y) = 4y+2x, Q(x,y) = 3x+2y, и контур С образован линиями 16y = 9x^3, y = 9, x = 0.
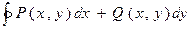 = = 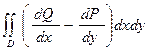 = =
= 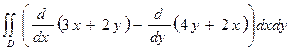 = =
= 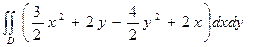 = =
= 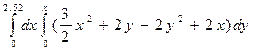 = =
= 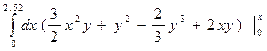 = =
= 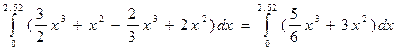 = =
= 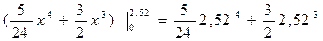 =32,4060912, =32,4060912,
где пределы интегрирования были получены:
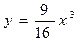 и у = 9, то и у = 9, то 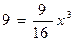 откуда х = откуда х = 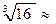 2,52. 2,52.
14. Даны поле 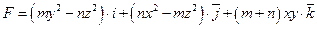 и пирамида с вершинами и пирамида с вершинами 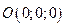 , , 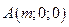 , ,  , ,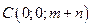 . Найти при m=3, n=4: . Найти при m=3, n=4:
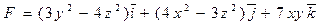
O(0:0:0), A(3:0:0), B(0:4:0), C(0:0:7).
а) поток поля 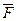 через грань через грань 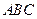 пирамиды в направлении нормали, составляющей острый угол с осью пирамиды в направлении нормали, составляющей острый угол с осью 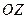 ; ;
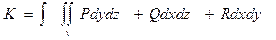 = =
= 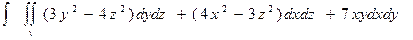 = =
=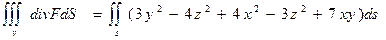 = =
=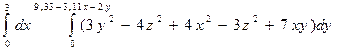 = =
=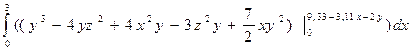 =… =…
после подстановки и преобразования однородных членов получим:
… = 8423,43 - 3336,03*у - 293,9*z^2 +118,98*у^2 – 24y^3 + 42y*z^2, т.е.
поток поля
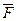 = 8423,43 - 3336,03*у - 293,9*z^2 +118,98*у^2 – 24y^3 + 42y*z^2. = 8423,43 - 3336,03*у - 293,9*z^2 +118,98*у^2 – 24y^3 + 42y*z^2.
б) поток поля 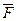 через внешнюю поверхность пирамиды с помощью теоремы Остроградского – Гаусса; через внешнюю поверхность пирамиды с помощью теоремы Остроградского – Гаусса;
в) циркуляцию поля 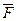 вдоль замкнутого контура вдоль замкнутого контура 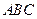 ; ;
с помощью теоремы Стока (обход контура происходит в положительном направлении относительно внешней нормали к поверхности пирамиды).
rot(F) = 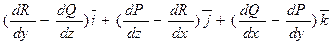 , ,
в нашем случае 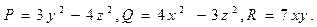
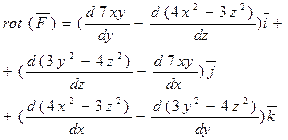
15. Найти первообразные и вычислить значение определенного интеграла:
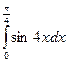 = = 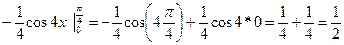 . .
|