Курсовая работа
ГЕНЕРАЦИЯ ПОЛИНОМОВ
Оглавление
Введение
Глава 1. Теоретическая часть по генерации полиномов
1.1 Теория полиномов
1.1.1 Основные определения, используемые в теории полиномов
1.1.2 Определение полинома
1.1.3 Основные свойства полиномов
1.1.4 Используемые в исследовании теоремы и их доказательства
1.2 Генерация полиномов
Глава 2. Практическая часть по генерации полиномов
2.1 Алгоритм генерации полиномов.
2.2 Написание программы, реализующей алгоритм генерации полиномов
2.2.1 Преодоление проблем, возникших при написании программы
2.2.2 Описание и пояснение некоторых частей программы
2.3 Листинг программы, реализующей алгоритм генерации полиномов
Заключение
Список использованных источников и литературы
Приложение
Введение
В данной курсовой работе рассмотрена проблема генерации полиномов (многочленов) по их введенным корням. Целью курсовой работы явилась разработка действенного алгоритма и написание на его основе программы, которая генерирует полином по его введенным корням. Проблема разработки алгоритма для генерации полиномов и написание на его основе программы является практически актуальной, так как ни для кого не секрет, что в последнее время на рынке литературы широко распространены так называемые «решебники». В них можно найти не только решения к заданиям из учебников, но и к заданиям из методической литературы, из которой учителя составляют контрольные и прочие работы для проверки знаний учащихся. В связи с этим, знания учащихся снижаются, а «успеваемость», которая перестала быть истинным критерием знаний учащегося, растет. Поэтому у учителей остается один выход – самим составлять проверочные работы. Однако временные возможности учителя ограничены, и он просто не в состоянии составить оригинальные задания на целый класс. Составленный алгоритм и программа, реализующая его, способны облегчить труд учителя в свете этой проблемы, так как за очень короткое время программный продукт способен сгенерировать полином по его введенной степени и корням. Соответственно, не прикладывая ни каких больших умственных усилий, а значит и больших временных ресурсов, учитель сможет составить множество оригинальных заданий, при этом у него останется время для других не менее важных дел.
Реклама

Данная курсовая работа состоит двух глав, включающих в себя каждый несколько параграфов и подпунктов.
В первой главе приведена теоретическая часть по генерации полиномов, включающая основные понятия и определения теории полиномов, основные теоремы алгебры и теории полиномов, дающие научную основу для разработки алгоритма генерации полиномов и написании на его основе программы.
Во второй главе рассказывается об основных проблемах, с которыми я столкнулся при составлении алгоритма и написании программы, приводится алгоритм генерации полиномов, описываются некоторые важные части программы, основывающейся на алгоритме, и приводится листинг программного продукта.
В заключении говорится о проблемах, с которыми столкнулся при составлении алгоритма и написании на его основе программы и о путях усовершенствования предложенного алгоритма и программы.
Глава 1. Теоретическая часть по генерации полиномов
1.1 Теория полиномов
1.1.1 Основные определения, используемые в теории полиномов
В первой главе этот пункт можно назвать одним из важнейших, так как в его содержании будут приведены определения основных понятий алгебры и теории полиномов, без которых не представлялось бы возможным понимание всего того, о чем будет говориться в остальных параграфах и главах.
Определение 1.
Множество – набор, совокупность, собрание каких-либо объектов, называемых его элементами, обладающими общим для всех них характеристическим свойством. [4, С. 382]
Определение 2.
Бинарная операция – правило, по которому каждой паре (a, b) элементов множества G однозначно ставится в соответствие некоторый элемент с того же множества G. [7, С. 11]
Определение 3.
Множество R, в котором заданы две бинарные операции + (сложение) и (умножение), называется полем, если выполняются следующие условия (аксиомы поля):
Сложение:
1. Коммутативность: a + b = b + a.
2. Ассоциативность: a + (b + c) = (a + b) + c.
3. Существование нуля: существует такой элемент 0,
что а + 0 = а для любого элемента а.
4. Существование противоположного: для любого элемента, а существует такой элемент (-а), что а + (-а) = 0.
Умножение:
1. Коммутативность: a ∙ b = b ∙ a.
2. Ассоциативность: a ∙ (b ∙ c) = (a ∙ b) ∙ c.
3. Существование единицы: существует такой элемент 1, что а∙1 = а для всякого элемента а.
4. Существование обратного: для любого элемента а ≠ 0 существует такой элемент а-1
, такой что а ∙ а-1
= 1.
Реклама

Сложение и умножение:
Дистрибутивность: a ∙ (b + c) = a ∙ b + а ∙ c. [2, С. 16]
Определение 4.
Коммутативным кольцом называется множество, в котором выполняются аксиомы поля, кроме, может быть, требования существования обратного элемента а-1
для любого а ≠ 0. [2, С. 23]
Определение 5.
Пусть S – множество. Отображение S * S → S – закон композиции – общее название для операции, производящей из двух элементов a, b S третий элемент c S третий элемент c S. [4, С. 279] S. [4, С. 279]
Определение 6.
Моноид – множество G с ассоциативным законом композиции. [4, С. 386]
Определение 7.
Если f(c) = 0, т.е. многочлен f(x) обращается в нуль при подстановке в него числа с вместо неизвестного, то с называется корнем многочлена f(x). [1, С. 144]
Определение 8.
Ненулевой элемент кольца, произведение которого на некоторый ненулевой элемент равно нулю, называется делителем нуля. [4, С. 176]
Определение 9.
Кольцо называется целостным (или областью целостности), если оно коммутативно и не содержит делителей нуля. [2, С. 26]
Определение 10.
Многочлен называется приводимым в кольце многочленов, если у него существуют делители со степенью больше нуля, но меньше степени полинома, иначе неприводимым. [6, С. 54]
1.1.2 Определение полинома
В математике и ее разделах существует несколько определений такого понятия как полином. Здесь и далее будем называть полином также степенным многочленом или просто многочленом. Приведем некоторые из них.
Первое определение взято из [3, С. 60]
Пусть R – некоторое кольцо. Построим с помощью нового, не принадлежащего кольцу R, символа х выражение вида f(х) = ∑аv
xv
, в которых суммирование ведется по какому-то конечному множеству целочисленных значений индекса v≥0 и «коэффициенты» аv
принадлежат кольцу R. Такие выражения называются многочленами; символ х называется переменной, v – степенью полинома.
Второе определение взято из [7, С. 131-133]
Пусть S – некоторое множество и N – моноид натуральных чисел. Обозначим через N(S) множество функций S → N, которые равны 0 для почти всех элементов из S. Пусть х S и t S и t N. Всякий элемент р N. Всякий элемент р N(S) имеет единственное представление в виде произведения N(S) имеет единственное представление в виде произведения 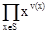 , где v: S→N – отображение, для которого v(x) = 0 при почти всех х. Такое произведение назовем примитивным многочленом и будем обозначать , где v: S→N – отображение, для которого v(x) = 0 при почти всех х. Такое произведение назовем примитивным многочленом и будем обозначать 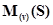 или просто или просто 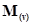 . .
Пусть А- коммутативное кольцо. Тогда можно образовать множество моноидов A[N(S)] над А, которую будем называть кольцом многочленов от S над A. По определению всякий элемент из A[N(S)] имеет единственное представление в виде линейной комбинации 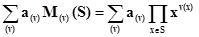 , где (v) пробегает все отображения множества S в N, обращающиеся в ноль для почти всех (v). Элементы из А[N(S)] называются многочленами от S над А. Элементы , где (v) пробегает все отображения множества S в N, обращающиеся в ноль для почти всех (v). Элементы из А[N(S)] называются многочленами от S над А. Элементы 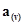 называются коэффициентами многочлена. Если S состоит из одного символа Х, то всякий многочлен может быть записан в виде называются коэффициентами многочлена. Если S состоит из одного символа Х, то всякий многочлен может быть записан в виде
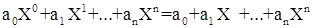 , ,
где 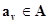 и n – некоторое целое число ≥ 0, называющееся степенью полинома. и n – некоторое целое число ≥ 0, называющееся степенью полинома.
Ниже приведенное определение взято из [1, С. 130]
Многочленом (или полиномом) n-й степени от неизвестного х называется сумма выражений с целыми степенями:
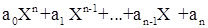 . .
Коэффициенты 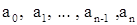 будем считать произвольными числами, причем старший коэффициент будем считать произвольными числами, причем старший коэффициент 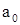 должен быть отличен от нуля. Для сокращенной записи многочленов употребляются символы f(x), g(x) и т.д. должен быть отличен от нуля. Для сокращенной записи многочленов употребляются символы f(x), g(x) и т.д.
В данной курсовой работе можно использовать любое из приведенных определений полинома, но в общем последнее определение полинома проще для понимания, но имеет не мене глубокий смысл, чем остальные, так как позволяет взглянуть на полином как на некоторое формальное выражение вполне определенное набором своих коэффициентов (что гораздо упрощает работу с полиномами при их генерации) с одной стороны и как на функцию от переменного Х (с точки зрения математического анализа) с другой стороны.
1.1.3 Основные свойства полиномов
1. Равенство одного полинома другому.
Два многочлена f(x) и g(x) будут считаться равными (или тождественно равными), f(x) = g(x), в том случае, если равны их коэффициенты при одинаковых степенях неизвестного. [1, С. 131]
2. Сложение и умножение полиномов.
Пусть 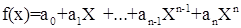 и и 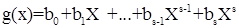 , где , где 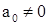 , , 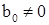 , n, s – степени многочленов f(x) и g(x). Если n ≥ s (иначе переобозначим степени полиномов), то их суммой называется многочлен , n, s – степени многочленов f(x) и g(x). Если n ≥ s (иначе переобозначим степени полиномов), то их суммой называется многочлен 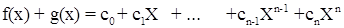 , коэффициенты которого получаются сложением коэффициентов f(x) и g(x), стоящих при одинаковых степенях переменного, т.е. , коэффициенты которого получаются сложением коэффициентов f(x) и g(x), стоящих при одинаковых степенях переменного, т.е. 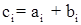 , i = 0, 1, …, n. Степень суммы равна n, если n ≥ s, но при n = s она может оказаться меньше n, а именно в том случае если , i = 0, 1, …, n. Степень суммы равна n, если n ≥ s, но при n = s она может оказаться меньше n, а именно в том случае если 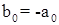 . [1, С. 132] . [1, С. 132]
Произведением многочленов f(x) и g(x) называется многочлен 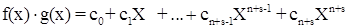 , коэффициенты которого определяются следующим образом , коэффициенты которого определяются следующим образом 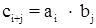 , так как , так как 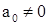 , , 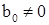 , то , то 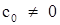 , поэтому степень произведения многочленов равна n + s. [1, С. 132] , поэтому степень произведения многочленов равна n + s. [1, С. 132]
3. Замкнутость относительно сложения и умножения. Исходя из первых двух свойств многочлена, очевидно, что складывая или перемножая два каких-либо многочлена от одного и того же переменного с коэффициентами из К, мы получим однозначно многочлен с коэффициентами из того же кольца К.
1.1.4 Используемые в исследовании теоремы и их доказательства
Т1.
[1, С. 134]
Для любых двух многочленов f(x) и g(x) можно на найти такие многочлены q(x) и r(x), что
f(x) = g(x) ∙ q(x) + r(x), (1.1)
причем степень r(x) меньше степени g(x) или же r(x) = 0. Многочлены q(x) и r(x), удовлетворяющие этому условию определяются однозначно.
Доказательство.
[1, С. 134-135]
Докажем сперва вторую половину теоремы. Пусть существуют еще многочлены q1(x) и r1(x), также удовлетворяющие равенству
f(x) = g(x) ∙ q1(x) + r1(x), (1.2)
причем степень r1(x) меньше степени g(x) или равна нулю. Приравнивая друг другу правые части равенств (1.1) и (1.2), получим:
g(x) ∙ [q(x) – q1(x)] = r1(x) – r(x).
Степень правой части этого равенства меньше степени g(x), степень же левой части была бы при 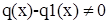 больше или равна степени g(x). Поэтому должно быть q(x) – q1(x) = 0, т.е. q(x) = q1(x), а тогда и r(x) = r1(x), что и требовалось доказать. больше или равна степени g(x). Поэтому должно быть q(x) – q1(x) = 0, т.е. q(x) = q1(x), а тогда и r(x) = r1(x), что и требовалось доказать.
Переходим к доказательству первой половины теоремы. Пусть многочлены f(x) и g(x) имеют соответственно степени n и s. Если n < s, то можно положить q(x) = 0, r(x) = f(x). Если же n ≥ s, то воспользуемся методом деления многочленов с действительными коэффициентами, расположенных по убывающим степеням неизвестного. Пусть
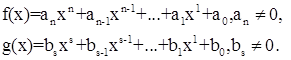
Полагая
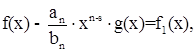 (1.3) (1.3)
мы получаем многочлен, степень которого меньше n. Обозначим эту степень через n1, а старший коэффициент многочлена f1
(x) – через аn
1
. Положим, далее, если все еще n1 ≥ s,
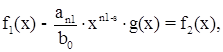 (1.4) (1.4)
Обозначим эту степень через n2, а старший коэффициент многочлена f2
(x) – через аn
2
. Положим, далее, если все еще n2 ≥ s,
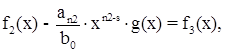 (1.5)и т.д. (1.5)и т.д.
Так как степень многочленов f1
(x), f2
(x), … убывают, n > n1 > n2 > …, то мы дойдем после конечного числа шагов до такого многочлена fk
(x),
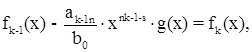 (1.k) (1.k)
степень которого nk меньше s, после чего наш процесс останавливается. Складывая теперь равенства (1.3), (1.4), (1.5), …, (1.k) мы получим:
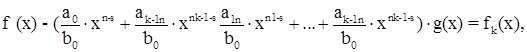
т.е. многочлены
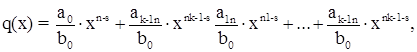

Действительно удовлетворяют равенству (1.2), причем степень r(x) действительно меньше степени g(x).
Т2.
[1, С. 135]
Многочлен g(x) тогда и только тогда будет делителем многочлена f(x), если существует многочлен q(x), удовлетворяющий равенству
f(x) = g(x) 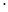 q(x) (2.1) q(x) (2.1)
Доказательство.
[1, С. 135-136]
Если g(x) является делителем для f(x), то в качестве q(x) следует взять частное от деления f(x) на g(x).
Обратно, пусть многочлен q(x), удовлетворяющий равенству (2.1), существует. Из Т1 о единственности многочленов q(x) и r(x), удовлетворяющих равенству f(x) = g(x) ∙ q(x) + r(x) и условию, что степень r(x) меньше степени g(x), в нашем случае следует, что частное от деления f(x) на g(x) равно q(x), а остаток равен нулю.
Т3.
[3, С. 106]
Если а – корень многочлена f(x), то f(x) делится на х – а.
Доказательство.
[3, С. 106 -107]
Деление f(x) на х – а дает равенство f(x) = (x –a) ∙ q(x) +r(x). Подставим в это равенство х = а: 0 = r(x), откуда f(x) = (x –a) ∙ q(x).
Т4. Основная теорема алгебры.
[1, С. 147]
Всякий многочлен с любыми числовыми коэффициентами, степень которого не меньше единицы имеет хотя бы один корень, в общем случае комплексный.
Доказательство.
См. [1, C.147 – 156]
Следствие 4.1
[1, С. 156]
Многочлен f(x) степени n над полем комплексных чисел имеет каноническое разложение с точностью до множителя нулевой степени вида f(x)=c ∙ (x – a1
) ∙ (x – a2
) ∙ … ∙ (x – an
). Причем это разложение единственное.
Доказательство.
См. [1, С. 156-157]
Следствие 4.2
Всякий многочлен f(x) степени n, n ≥ 1, с любыми числовыми коэффициентами имеет n корней, если каждый корень считать столько раз, какова его кратность.
Доказательство.
См. [1, С. 157]
Из всех приведенных теорем и следствий наибольшее значение для данной курсовой работы имеют следствия 4.1 и 4.2, так как в них говориться, что любой многочлен в общем случае может разлагаться на многочлены первой степени с точностью до множителя нулевой степени, т.е. с точностью до числового коэффициента, и их количество с учетом кратности равно степени разлагаемого многочлена и что многочлены, входящие в каноническое разложение, содержат в себе все корни разлагаемого полинома, соответственно с учетом их кратности.
Это не маловажно, так как теперь можно говорить о том, что, имея степень генерируемого полинома и его корни, мы можем с точностью до числового коэффициента определить и получить необходимый полином указанной степени.
1.2 Генерация полиномов
Генерация достаточно молодая и полностью не исследованная область
информатики и программирования. Дать точного и полного определения, что такое генерация пока еще не возможно. Под генерацией в общем случае понимается процесс динамического изменения некоторых программных параметров. Теоретически генерация может быть случайной, однако на практике случайную генерацию организовать практически не возможно. Так, например, генерация случайных чисел (в действительности псевдо случайных) зависит от многих параметров (время, дата и т.д.). Тема этой курсовой работы генерация полиномов. В программе, реализующей алгоритм генерации полинома, происходит заведомо неслучайная генерация коэффициентов полинома, так как она зависит от двух параметров: степени полинома и его корней
Глава 2. Практическая часть по генерации полиномов
2.1 Алгоритм генерации полиномов
Исследовав теоретическую часть по проблеме генерации полиномов, приступил к практическому применению полученных знаний. Прежде, чем приступать к написанию кода программы, генерирующей полиномы по введенной пользователем степени и корням, составил алгоритм для решения данной задачи.
Алгоритм.
1. Ввести степень генерируемого полинома.
2. Если степень не была введена или был введен символ, не являющийся цифрой, или было введено число меньше двух, то выдать сообщение об ошибке и перейти к пункту 1, иначе, при корректном вводе, перейти к пункту 3.
3. Организовать цикл (количество итераций равно степени генерируемого полинома) для ввода корней генерируемого полинома.
4. Ввести корни генерируемого полинома.
5. Если корень не был введен или был введен символ, не являющийся цифрой, то выдать сообщение об ошибке и перейти к пункту 4, иначе, при корректном вводе, перейти к пункту 6.
6. После окончания работы цикла произвести перемножение введенных корней генерируемого полинома в соответствии с правилами перемножения полиномов (см. пункт 1.1.3.2)
7. Вывести получившийся полином в порядке убывания степеней переменной на экран.
2.2 Написание программы, реализующей алгоритм генерации полиномов
2.2.1 Преодоление проблем, возникших при написании программы
При написании кода программы, реализующей алгоритм генерации полиномов, столкнулись с рядом трудностей.
Во-первых, необходимо было реализовать проверку вводимых данных, чтобы вводимые значениями были только цифры и числа. Для преодоления первой проблемы был разработан следующий алгоритм, реализация которого будет приведена ниже.
1. Инициализировать цикл с постусловием.
2. Ввести значение в виде строки.
3. Инициализировать цикл (количество итераций равно длине введенной пользователем строки).
4. Перемещаться во введенной строке посимвольно.
5. Если символ цифра перейти к пункту 6, иначе перейти к пункту 8.
6. Переводим символ в цифру.
7. Прибавляем цифру к числу, которое будет являться переводом введенной строки, если она число, предварительно умноженное его на десять.
8. Выдаем сообщение об ошибке и переходим к пункту 2.
9. Запоминаем получившееся число при корректном вводе.
Второй проблемой явилось переполнение типа данных – longпри перемножении (в данной программе, написанной на языке С). Однако она была решена при написании функций проверки при перемножении и общей проверки коэффициентов генерируемого полинома, которые будут приведены ниже.
Третья проблема – переполнение буфера. При написании программы пришлось увеличить буфер для ввода значений, но при считывании рассматривать только первые девять символов, чтобы заведомо не превысить максимальное значение используемого типа, и, если было введено более девяти символов, то выдать сообщение об ошибке и попросить пользователя заново ввести значение.
Четвертая проблема – хранение введенных данных. Для ее преодоления было использовано четыре массива; в первом (массив m)будут храниться все корни генерируемого полинома (его размер – 2∙n, где n – степень генерируемого полинома), второй и третий – вспомогательные (участвуют в перемножении), в третьем (массив b) будет храниться корень генерируемого многочлена, взятый из первого массива, (его размер – 2); во втором (массив a) вначале храниться корень генерируемого многочлена из первого массива, а после первого перемножения в него будет перезаписываться результат перемножения для следующего выполнения этой операции (размер – n+1); последний массив (массив c) – результирующий, содержит все коэффициенты генерируемого многочлена после перемножения (размер n+1).
2.2.2 Описание и пояснение некоторых частей программы
В данном пункте будут приведены некоторые части программы, реализующей алгоритм генерации полиномов, с пояснениями.
1. Функция реализующая нахождение модуля числа типа long
long Modul(long a)
{
if (a<0)
return (-a);
else
return (a);
}
Если функция получила отрицательное число, то она возвращает число с противоположным знаком, в противном случае само число.
Входные данные – число типа long.
Выходные данные – число типа long.
2. Функция проверки возможности выхода за диапазон типа long при перемножении корней генерируемого полинома.
int provper(long a, long b)
{
if(b==0 || a==0)
return(1);
else
if(Modul(a)<MAXLONG/Modul(b))
return(1);
else
return(0);
}
Если одно из переданных функции значений равно нулю, то функция возвращает единицу, иначе, если абсолютное значение одного из полученных функций значений меньше, чем число равное частному от деления максимального значения типа long на другое введенное значение, т.е., если при перемножении полученных функцией значений, их произведение не выходит за диапазон типа long, то функция возвращает единицу, в противном случае – ноль.
Входные данные – два числа типа long.
Выходные данные – число типа int (единица или ноль).
3. Функция проверки выхода за диапазон при сложении коэффициентов генерируемого полинома при одинаковых степенях переменного.
int provsum(long a, long b)
{
if(Modul(a)<(MAXLONG-Modul(b)))
return(1);
else
return(0);
}
Если одно из переданных функции значений меньше, чем разность максимального значения типа long и другого переданного значения, то функция возвращает единицу, в противном случае – ноль.
Входные данные – два числа типа long.
Выходные данные – число типа int (единица или ноль).
4. Функция, перемножающая два многочлена.
void peremnoz (long *a, int n, long *b, long *c)
{
long z=0;
int i,j;
for ( i=0; i<n;i++)
for( j=0; j<2; j++)
{
if(provper(*(a+i),*(b+j))==1)
z=(*(a+i)*(*(b+j)));
else
*(c+(i+j))=MAXLONG;
if(provsum(z,*(c+(i+j)))==1)
*(c+(i+j))+=z;
else
*(c+(i+j))=MAXLONG;
}
}
В функции инициализируются два цикла, один из которых вложен в другой. Внешний пробегает по всем коэффициентам первого многочлена, участвующего в перемножении (в программе реализуется в виде массива a, а коэффициенты многочлена – элементы массива а), внутренний – по коэффициентам второго многочлена (в программе – в виде массива b, коэффициенты многочлена – элементы массива b). Если перемножение коэффициентов (элементов массивов) возможно (начинает работу функция intprovper(longa, longb)), т.е. не произойдет выход за диапазон типа long, то результат перемножения записываем в переменную z, в противном случае, соответствующему коэффициенту результирующего многочлена (в программе – массив c, коэффициенты многочлена – элементы массива) присваивается максимальное значение (MAXLONG) типа longи внутренний цикл прекращает свою работу. Если произведение коэффициентов массива не вышло за диапазон типа long, то проверяем: не произойдет ли выход за диапазон типа long при сложении получившегося значения (храниться в переменной z) с коэффициентом результирующего многочлена (элемент массива c) (начинает работу функция intprovsum(longa, longb)); если сложение возможно, то к соответствующему коэффициенту результирующего многочлена (элемент массива c) прибавляется результат перемножения коэффициентов первых двух многочленов (значение переменной z), иначе, соответствующему коэффициенту результирующего многочлена присваивается максимальное значение (MAXLONG) типа long.
Работа функции перемножения основана на свойствах полинома (см. пункт 1.1.3).
Входные данные: три указателя типа long (на массивы, участвующие в перемножении, и на результирующий массив), число типа int (количество элементов первого массива).
5. Функция проверки нахождения коэффициентов генерируемого полинома в диапазоне используемого типа.
int prov(long *a, int n)
{
int i, y=0;
for(i=0;i<n+1;i++)
if(Modul(*(a+i))==MAXLONG)y++;
return (y);
}
В функции инициализируется цикл (количество итераций равно степени генерируемого многочлена, увеличенной на единицу). Производим движение по коэффициентам генерируемого многочлена (элементам массива a); если абсолютное значение какого-либо коэффициента генерируемого многочлена равно максимальному значению (MAXLONG) типа long, то значение флага (переменной y), изначально равное нулю, увеличиваем на единицу.
Входные данные: указатель типа long (на массив a), число типа int (степень генерируемого полинома, увеличенная на единицу).
Выходные данные: число типа int.
6. Часть программы, переводящая символ, являющийся цифрой, в число.
{
w=s[i]-'0';
q=10*q+w;
x=1;
}
Если введенный символ – цифра, то из кода этого символа вычитаем из кода символа код нуля и получаем число, соответствующее введенному символу.
2.3 Листинг программы, реализующей алгоритм генерации полиномов
#include <stdio.h>
#include <conio.h>
#include <math.h>
#include <string.h>
#include <ctype.h>
#include <stdlib.h>
#include <values.h>
#include <time.h>
long Modul(long a)
{
if (a<0) return (-a);
else return (a);
}
int provper(long a, long b)
{
if(b==0 || a==0)return(1);
else
if(Modul(a)<MAXLONG/Modul(b)) return(1);
else return(0);
}
int provsum(long a, long b)
{
if(Modul(a)<(MAXLONG-Modul(b))) return(1);
else return(0);
}
void peremnoz (long *a, int n, long *b, long *c) {
long z=0;
int i,j;
for ( i=0; i<n;i++)
for( j=0; j<2; j++)
{
if(provper(*(a+i),*(b+j))==1)
z=(*(a+i)*(*(b+j)));
else *(c+(i+j))=MAXLONG;
if(provsum(z,*(c+(i+j)))==1)
*(c+(i+j))+=z;
else *(c+(i+j))=MAXLONG;
}
}
int prov(long *a, int n)
{
int i, y=0;
for(i=0;i<n+1;i++)
if(Modul(*(a+i))==MAXLONG)y++;
return (y);
}
void main()
{
int stepen=0, n=2, w, x=0, i, k, f=1;
long *a, *b, *m, *c, q=0, z;
char *s;
s=(char *) calloc(900, sizeof(char ));
clrscr();
do{
printf("Введите степень не меньшую, чем 2 и не большую, чем 100:");
gets(s);
if(strlen(s)<1)
{
printf("\nНе было введено значения. Повторите ввод\n");
x=0;
}
if(strlen(s)>9)
{
printf("\nВведено более 9 символов. Повторите ввод\n");
x=0;
}
else
{
for( i=0;i<strlen(s); i++)
if (isdigit(s[i])!=0)
{
w=s[i]-'0';
q=10*q+w;
x=1;
}
else
{
printf("\nВведен символ или пробел. Повторите ввод\n");
x=0;
break;
}
stepen=q;
free(s);
s=(char *) calloc(900, sizeof(char ));
q=0;
w=0;
}
}while( stepen<2 || stepen>100 || x==0);
clrscr();
a=(long *) calloc(stepen+1, sizeof(long ));
b=(long *) calloc(2, sizeof(long ));
m=(long *) calloc((stepen)*2, sizeof(long ));
c=(long *) calloc(stepen+1, sizeof(long ));
for(i=0;i<stepen*2;i++)
{
if(i%2==0)
{
do{
q=0;
printf("Введитекореньмногочлена#%d ", (i/2)+1);
gets(s);
if(strlen(s)<1)
{
printf("\nНе было введено значения. Повторите ввод\n");
x=0;
}
if(strlen(s)>9)
{
printf("\nВведено более 9 символов. Повторите ввод\n");
x=0;
}
else
{
if(s[0]=='-')
for(k=1; k<strlen(s); k++)
if (isdigit(s[k])!=0)
{
w=s[k]-'0';
q=10*q+w;
x=1;
f=-1;
}
else
{
printf("\nВведен символ или пробел. Повторите ввод\n");
x=0;
break;
}
else
for( k=0; k<strlen(s);k++)
if (isdigit(s[k])!=0)
{
w=s[k]-'0';
q=10*q+w;
x=1;
f=1;
}
else
{
printf("\nВведен символ или пробел. Повторите ввод\n");
x=0;
break;
}
}
free(s);
s=(char *) calloc(900, sizeof(char ));
} while(x==0);
if(f==1)
{
*(m+i)=q;
q=0;
w=0;
*(m+i)=-*(m+i);
}
else
if(f==-1)
{
*(m+i)=q;
q=0;
w=0;
}
}
else *(m+i)=1;
}
for(i=0;i<2;i++)
{
*(a+i)=*(m+i);
*(b+i)=*(m+2+i);
}
for( k=0;k<stepen-1;k++)
{
peremnoz(a,n,b,c);
for( w=0; w<n+1; w++)
{
*(a+w)=*(c+w);
*(c+w)=0;
}
for(w=0;w<2;w++)
*(b+w)=*(m+(i*n)+w);
n++;
}
clrscr();
if(prov(a,stepen)!=0)
{
printf("\nПроизошел выход за диапазон типа.");
printf("\n\nПри следующем использовании данного программного продукта будьте осторожны с\n вводимыми значениями степени и корней");
printf("\n\nСпасибо, что пользовались моим прогаммным продуктом!:)");
printf("\n\nНажмите любую кнопку.");
}
else
{
printf("\Генериремый полином:\n");
printf("x^%d",stepen);
for(i=stepen-1;i>0;i--)
{
if(i==1)
if(*(a+i)==-1) printf("-x");
else
if(*(a+i)==1) printf("+x");
else
if(*(a+i)<0) printf("%ldx",*(a+i));
else
if(*(a+i)>0) printf("+%ldx",*(a+i);
else n++;
else
if(*(a+i)==-1) printf("-x^%d",i);
else
if(*(a+i)==1) printf("+x^%d",i);
else
if(*(a+i)<0)
printf("%ldx^%d",*(a+i),i);
else
if(*(a+i)>0)
printf("+%ldx^%d",*(a+i),i);
else n++;
}
if(a[0]<0) printf("%ld",a[0]);
else
if(a[0]>0) printf("+%ld",a[0]);
else n--;
printf("=0");
printf("\n\nСпасибо, что пользовались моим прогаммным продуктом!:)");
printf("\n\nНажмите любую кнопку.");
}
free(a);
free(b);
free(c);
free(m);
free(s);
getch();
}
Входные данные: числа типа long.
Выходные данные: числа типа long.
1. При введенных значениях степени и корней генерируемого полинома, не допускающих выход за диапазон типа long, – коэффициенты генерируемого многочлена с соответствующими степенями переменных.
2. При не корректно введенных значениях:
1. Если при вводе степени введено число меньше двух и больше 100, то выдается сообщение о не корректном вводе с просьбой повторить ввод заново.
2. Если не было введено значение степени или корня полинома, то выдается сообщение о не корректном вводе с просьбой повторить ввод заново.
3. Если было введено более девяти символов, то выдается сообщение о не корректном вводе с просьбой повторить ввод.
4. Если был введен символ или пробел, то выдается сообщение о не корректном вводе с просьбой повторить ввод.
5. Если произошел выход за диапазон типа long, то выдается сообщение о не корректном вводе с просьбой при следующем использовании данного программного продукта быть аккуратными при вводе степени генерируемого полинома и его корней, чтобы не допустить выход за диапазон используемого типа.
Результаты теста данного программного продукта можно увидеть в Приложении.
В заключение данной курсовой работы хотелось бы кратко сказать о проделанной работе, о проблемах, с которыми столкнулся при выполнении поставленной цели, и о перспективах развития и улучшения данного программного продукта.
Целью данной курсовой работы было составить алгоритм генерации полиномов по введенной степени и корням и написать программу, реализующую этот алгоритм.
Чтобы выполнить поставленную цель, необходимо было решить три задачи:
1. Поиск литературы по предмету данной курсовой работы.
2. Составление алгоритма для выполнения поставленной цели.
3. Написание программы, реализующей составленный алгоритм.
При решении третьей задачи столкнулся с рядом трудностей:
1. Организацией ввода значений и проверки его корректности. Необходимо было проверять, чтобы введенные значения являлись только числами.
2. Организацией хранения введенных данных для удобного обращения к ним в ходе написания и работы программы.
3. Проверки, чтобы при работе программы не произошел выход за диапазон используемого типа.
Основными источниками, помогавшими выполнить поставленную цель, явились:
1. Книги по линейной алгебре, в которых содержался материал по теории полиномов.
2. Книги по информатике и программированию.
3. Курс лекций, прочитанных в рамках дисциплин «Программирование на языке Си», «Информатика», «Структуры и алгоритмы компьютерной обработки данных», «Алгебра и теория чисел».
Результатом данной курсовой работы стал алгоритм генерации полиномов и написанная на его основе программа. Данная программа предназначена для работы с целыми числами, хотя алгоритм является действенным и при работе с вещественными числами, а при некоторых его усовершенствованиях (организации работы с мнимой частью) и с комплексными. Следовательно, одной из перспектив развития данного алгоритма является его улучшение для работы с комплексными числами, а программы – написание ее для работы со всеми числами: целыми, вещественными, комплексными.
Так же реально улучшить временную характеристику алгоритма и программы, если после проверки «не вышло ли произведение или сумма коэффициентов многочлена» за диапазон типа, если все же выход произошел, сразу же остановить работу алгоритма и программы и выдать пользователю сообщение об ошибке.
Чтобы более полно использовать возможности алгоритма, его лучше реализовывать на тех языках программирования, у которых типы данных имеют достаточно большие диапазоны.
Решив последнюю задачу, можно сразу решить такие задачи, как увеличение вводимого значения степени генерируемого полинома и количества вводимых символов и буфера.
Не трудно заметить, что при перемножении вещественных чисел с дробной частью количество цифр в дробной части их произведения будет равно, в общем случае, сумме количества символов перемножаемых чисел, поэтому количество символов в дробной части произведения при большом количестве символов в дробной части перемножаемых чисел достаточно быстро увеличивается.
Следовательно, одной из серьезнейших проблем при работе с вещественными и комплексными числами встает проблема точности, которую, в принципе на все сто процентов разрешить никогда не удастся, так как программист всегда будет ограничен в ресурсах, поэтому представить вещественные можно только лишь с определенной точностью, иногда вполне достаточной.
Надеюсь, что мой опыт в разработке подобных программных продуктов будет полезен другим людям, и данная программа из области исследования при выполнении курсовой работы, при условии, конечно же, его усовершенствования, выйдет в свет как полностью готовый к использованию программный продукт и будет востребован не только в целях методических разработок.
Список использованных источников и литературы
1. КурошА.Г. Курс высшей алгебры / А.Г. Курош. – М.: Наука, 1968. – 431с.
2. Шафаревич И.Р. Основные понятия алгебры / И.Р. Шафаревич. – Ижевск: Ижевская республиканская типография, 1999. – 348с.
3. Варден ван дер Б.Л. Алгебра / Б.Л. ван дер Варден. – М.: Наука, 1979. – 623с.
4. Математика. Большой энциклопедический словарь / Гл. ред. Ю.В. Прохоров. – 3-е изд. – М.: Большая Российская энциклопедия, 1998. – 848 с.: ил.
5. Подбельский В.В. Язык Си++: Учебное пособие. – 5 –е изд. / В.В. Подбельский. – М.: Финансы и статистика, 2003. – 560с.: ил.
6. Устян А.Е. Методические материалы по курсу «Алгебра и теория чисел» для студентов – государственников / А.Е. Устян. – Тула: Тул.гос.пед.ун –т им. Л.Н. Толстого, 1992. – 86с.
7. Зарисский О. Коммутативная алгебра. Том I / О. Зарисский, П. Самюэль. – М.: Издательство иностранной литературы, 1963. – 371с.
8. Ленг С. Алгебра / С. Ленг. – М.: Наука, 1999. – 564с.
Приложение
Таблица тестов
В таблице приведены результаты некоторых тестов программы.
Обратите внимание на то, что в скобках показаны некорректно введенные данные и сообщения программы об ошибках с просьбами повторить ввод.
| номер теста |
входные данные |
выходные данные |
| 1 |
2;
1, 2
|
x^2-3x+2=0 |
| 2 |
3;
1, 2, 3
|
x^3-6x^2+11-6=0 |
| 3 |
10;
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
|
x^10-10x^9+45x^-120x^7+210x^6-
-252x^5+210x^4-120x^3 + 45x^2-10x+1
|
| 4 |
4;
1234, 4321, 23 ,32
|
Произошел выход за диапазон типа |
| 5 |
2;
999999999, 1
|
x^2-10000000000x+999999999 |
| 6 |
2;
0 , 0
|
x^2=0 |
| 7 |
(-4),(1), 3;
(q), ( ), 0, 1, 100
|
(Введен символ или пробел повторите ввод), (Введите степень не меньшую, чем 2, и не большую, чем 100), (Введен символ или пробел повторите ввод), (Не было введено значения),
x^3-101x^2+100x=0
|
| 8 |
5;
-1, 1, -2, 2, 0
|
x^5-5x^3+4x=0 |
| 9 |
10;
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
|
x^10-45x^9+870x^8-9450x^7+63273x^6-
-269325x^5+723680x^4-1172700x^3+
+1026576x^2-362880x
|
| 10 |
25;
1, 2, 3, 4, 5, 6, 7, 8, 9, 9, 8, 7, 6, 5, 4, 3, 2, 1, 1, 2, 3, 4, 5, 6, 7
|
Произошел выход за диапазон типа |
|