 Министерство образования и науки РФ Министерство образования и науки РФ
Государственное образовательное учреждение
высшего профессионального образования
Владимирский государственный университет
Кафедра автоматизации технологических процессов
Реферат
по предмету: “
Моделирование систем”
на тему: ”Отделение корней. Графический и аналитический методыотделения корней”
Группа ЗАУ91-107
Руководитель
Кирилина А.Н.
Разработал студент
Ерёмин Е.С.
|
Содержание
1. Отделение корней............................................................................ 3
2. Графический метод.......................................................................... 4
3. Аналитический метод (табличный или шаговый).......................... 5
4. Метод половинного деления (Дихотомии)...................................... 9
1. Отделение корней
В общем случае отделение корней уравнения f(x)=0
базируется на
известной теореме, утверждающей, что если непрерывная функция f(x)
на
концах отрезка [a,b]
имеет значения разных знаков, т.е. f(a)×f(b)< 0
, то в указанном промежутке содержится хотя бы один корень. Например, для уравнения f(x)=x3
-6x+2=0
видим, что при  при при  что уже свидетельствует о наличии хотя бы одного корня. что уже свидетельствует о наличии хотя бы одного корня.
Для уравнения  видим, что видим, что  Обнаружив, что Обнаружив, что  устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело). устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
Если предварительный анализ функции затруднителен, можно “пойти в лобовую атаку”. При уверенности в том, что все корни различны, выбираем некоторый диапазон возможного существования корней (никаких универсальных рецептов!) и производим “прогулку” по этому интервалу с некоторым шагом, вычисляя значения f(x)
и фиксируя перемены знаков. При выборе шага приходится брать его по возможности большим для минимизации объема вычислений, но достаточно малым, чтобы не пропустить перемену знаков.
Этот метод основан на построении графика функции y=f(x). Если построить график данной функции, то искомым отрезком [a,b], содержащим корень уравнения (1), будет отрезок оси абсцисс, содержащий точку пересечения графика с этой осью. Иногда выгоднее функцию f(x) представить в виде разности двух более простых функций, т.е.  и строить графики функций и строить графики функций  и и  . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох. . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.
Реклама

Пример.
Графически решить уравнение  . .
Решение.
Запишем исходное уравнение в виде:  , т.е. , т.е.  и и  . .
Таким образом, корни данного уравнения могут быть найдены как абсциссы точек пересечения кривых  и и  . .
Теперь построим графики функций и определим интервал изоляции корня.

Рис. 1.
|
Из рис.1 видно, что корень находится на отрезке [1,2]. В качестве приближенного значения этого корня можно взять значение х=1.5. Если взять шаг по оси Ох меньше, то и значение корня можно получить более точное. |
Для отделения корней полезно помнить следующие известные теоремы:
1) если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. f(a)f(b)<0, то внутри этого отрезка содержится, по крайне мере, один корень уравнения f(x)=0;
2) если непрерывная и монотонная функция f(x) на отрезке [a,b] принимает на концах отрезка значения разных знаков, то внутри данного отрезка содержится единственный корень;
3) если функция f(x) непрерывна на отрезка [a,b] и принимает на концах отрезка значения разных знаков, а производная ее сохраняет постоянный знак внутри отрезка, то внутри отрезка существует корень уравнения (1) и притом единственный.
Если исходное уравнение имеет близкие корни или функция f(x) сложная, то для отделения отрезков изоляции можно воспользоваться методом деления отрезка на части (шаговым методом).
Сначала определяют знаки функции в граничных точках области. Затем отрезок разбивается с помощью промежуточных точек x=a1
,a2
,…. Если окажется, что в двух соседних точках ak
и ak
+1
функция f(x) имеет разные знаки, то в силу приведенной теоремы, можно утверждать, то на этом отрезке имеется по крайне мере один корень.
Теперь необходимо убедиться, что на выбранном отрезке находится единственный корень. Для этого можно проверить меняет ли знак производная функции f(x) на этом интервале.
Пример.
Найти интервалы изоляции корня уравнения 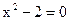 на [0,4] на [0,4]
Решение.
Построим таблицу значений, где 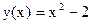 : :
| x |
y(x) |
| 0 |
-2 |
| 1 |
-1 |
| 2 |
2 |
| 3 |
7 |
| 4 |
14 |
Из таблицы значений видно, что функция y(x) меняет знак на отрезке [1,2], поэтому корень находится на этом отрезке.
Для отделения корней алгебраического уравнения (2) с действительными коэффициентами полезно помнить следующие известные теоремы алгебры:
1) если 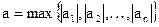 , , 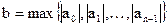 , то все корни уравнения (2) расположены в кольце , то все корни уравнения (2) расположены в кольце
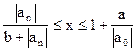 , (3) , (3)
2) если а максимум модулей отрицательных коэффициентов уравнения, 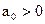 и первый отрицательный коэффициент последовательности и первый отрицательный коэффициент последовательности 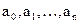 есть есть 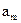 , то все положительные корни уравнения меньше , то все положительные корни уравнения меньше 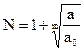 (если отрицательных коэффициентов нет, то нет и положительных корней). (если отрицательных коэффициентов нет, то нет и положительных корней).
3) если 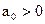 и при и при 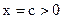 имеют место неравенства имеют место неравенства 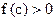 , , 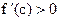 , ¼, , ¼, 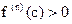 , то число с служит верхней границей положительных корней уравнения (2). , то число с служит верхней границей положительных корней уравнения (2).
Реклама

4) Пусть заданы многочлены
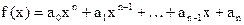 , ,
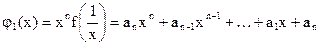 , ,
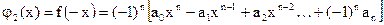 , ,
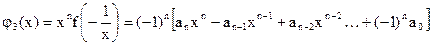
и N0
, N1
, N2
, N3
верхние границы положительных корней соответственно многочленов f(x), 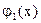 , , 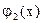 , , 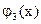 . Тогда все положительные корни уравнения (2) лежат на отрезке . Тогда все положительные корни уравнения (2) лежат на отрезке 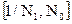 , а все отрицательные корни на отрезке , а все отрицательные корни на отрезке 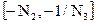 . .
Пример.
Отделить корни данного алгебраического уравнения, используя теорему 4: 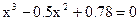 . .
Решение.
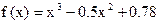 , ,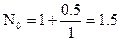 , ,
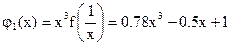 , , 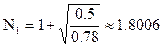 , ,
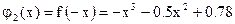 , , 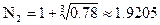 , ,
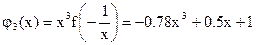 , , 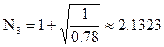 . .
Таким образом корни уравнения могут лежать на интервалах 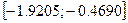 , , 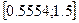 . .
Для определения количества действительных корней уравнения (2) необходимо воспользоваться теоремой Декарта
: число положительных корней уравнения (2) с учетом их кратности равно числу перемен знаков в последовательности коэффициентов 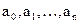 (при этом равные нулю коэффициенты не учитываются) или меньше этого числа на четное число. (при этом равные нулю коэффициенты не учитываются) или меньше этого числа на четное число.
Теорема Декарта не требует больших вычислений, но не всегда дает точное количество действительных корней уравнения (2).
Замечание.
Для определения количества отрицательных корней достаточно применить теорему Декарта к многочлену 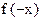 . .
Если уравнение (2) не имеет кратных корней на [a,b], то точное число действительных корней дает теорема Штурма.
Предположим, что уравнение (2)не имеет кратных корней. Обозначим через 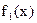 производную производную 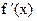 ; через ; через 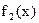 остаток от деления остаток от деления 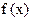 на на 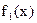 , взятый с обратным знаком; через , взятый с обратным знаком; через 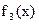 остаток от деления остаток от деления 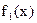 на на 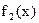 , взятый с обратным знаком и т.д., до тех пор пока не придем к постоянной. Полученную последовательность , взятый с обратным знаком и т.д., до тех пор пока не придем к постоянной. Полученную последовательность
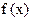 , , 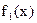 , , 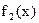 , …, , …, 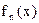 (4) (4)
назовем рядом Штурма.
Теорема Штурма:
Число действительных корней уравнения f(x)=0, расположенных на отрезке [a,b], равно разности между числом перемен знаков в последовательности (4) при х=a и числом перемен знаков в последовательности (4) при х=b.
Замечание.
Использование теоремы Штурма на практике, связано с большой вычислительной работой при построении рядя Штурма.
Пример.
Отделить корни данного алгебраического уравнения, используя теорему Штурма: 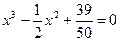
Решение.
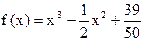 , ,
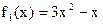 , ,
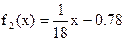 , ,
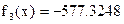
Построим таблицу для подсчета смены знаков:
| -¥ |
-1 |
-0.4 |
0.5 |
1 |
¥ |
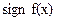 |
- |
- |
+ |
+ |
+ |
+ |
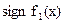 |
+ |
+ |
+ |
+ |
+ |
+ |
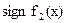 |
- |
- |
- |
- |
- |
+ |
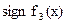 |
- |
- |
- |
- |
- |
- |
| Число перемен знаков |
2 |
2 |
1 |
1 |
1 |
1 |
Из таблицы подсчета смены знаков видно, что есть один корень данного уравнения, и он находится на [-1;-0.4].
Пусть дано уравнение (1), где функция f(x) непрерывна на отрезке [a,b] и f(a)f(b)<0. Для нахождения корня этого уравнения, принадлежащего данному отрезку [a,b], делим его пополам. Если значение 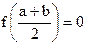 , то , то 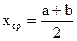 - корень уравнения. Если - корень уравнения. Если 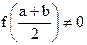 , то выбираем тот, из полученных отрезков , то выбираем тот, из полученных отрезков 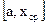 или или 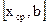 на концах которого функция f(x) имеет противоположные знаки. Новый отрезок полученный указанным способом на концах которого функция f(x) имеет противоположные знаки. Новый отрезок полученный указанным способом 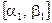 снова делим пополам и процесс снова повторяем. снова делим пополам и процесс снова повторяем.
Продолжая этот процесс, получим либо точное значение корня уравнения или бесконечную последовательность вложенных друг в друга отрезков 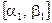 , , 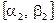 , …, , …, 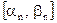 , … таких, что , … таких, что 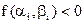 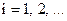 , причем , причем 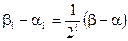 . .
Замечание.
Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, т.к. при увеличении точности существенно возрастает объем вычислительной работы.
Пример.
Уточнить корень уравнения 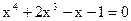 , лежащий на отрезке [0,1]. , лежащий на отрезке [0,1].
Решение.
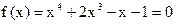 . .
1 этап: а=0, 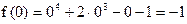 , ,
b=1, 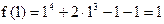 , ,
f(0)f(1)=-1<0
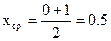 , , 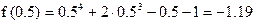
f(0)f(0.5)>0, значит корня на отрезке [0;0.5] нет.
f(0.5)f(1)<0, значит корень находится на [0.5;1].
2 этап: a=0.5, f(0.5)=-1.19
b=1, f(1)=1
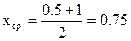 , , 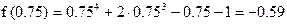
f(0.5)f(0.75)>0, значит корня на отрезке [0.5;0.75] нет.
f(0.75)f(1)<0, значит корень находится на [0.5;1].
Дальше процесс продолжается аналогичным образом.
Список используемой литературы
1. Пирумов У. Г.. Численные методы : учебное пособие для вузов по направлению "Прикладная математика" / У. Г. Пирумов .— 3-е изд., испр. — Москва : Дрофа, 2004 .— 221 с. : ил., табл. — (Высшее образование) .— Библиогр.: с. 216 .— Имен. указ.: с. 217 .— ISBN 5-7107-8777-9.
2. Киреев В. И.. Численные методы в примерах и задачах : учебное пособие для технических вузов / В. И. Киреев, А. В. Пантелеев .— Изд. 2-е, стер .— Москва : Высшая школа, 2006 .— 480 c. : ил., табл .— (Прикладная математика для втузов) .— Библиогр.: с. 477-480 .— ISBN 5-06-004763-6.
3. Катаева Л.Ю. Методическая разработка по курсу "Вычислительная математика" /РГОТУПС МПС РФ; Н. Новгород, 2003 г.
|