ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «КЕМЕРОВСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Математический факультет
Кафедра автоматизации исследований и технической кибернетики
Реферат
“Решение нелинейных уравнений методом деления отрезка пополам”
студента 3 курса
Ткаченко Ивана Сергеевича
Специальность 010501
«Прикладная математика и информатика»
Преподаватель:
Преслер В.Т.
КЕМЕРОВО 2009
Оглавление
1 Формулировка задачи
2 Математическая постановка задачи
2.1 Метод решения задачи
2.2 Способы ввода, вывода и организации данных
2.3 Исключительные ситуации и реакция на них
2.4 Модульная организация программы
2.5 Спецификация данных
2.6 Организация вычислительного процесса
3 Разработка блок-схемы алгоритма задачи
4 Создание программы на алгоритмическом языке
5 Построение тестов и отладка программы
1
Формулировка задачи
Найти корни нелинейного уравнения 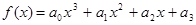 . Значения коэффициентов . Значения коэффициентов 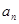 , границы отрезка интегрирования и значение допустимой погрешности задаются пользователем. , границы отрезка интегрирования и значение допустимой погрешности задаются пользователем.
Вычисление корня функции методом деления отрезка пополам.
Корень функции F(x) — это такое значение ее аргумента х*, при котором выполняется условие F(x*) = 0. Известно, что для решения такого уравнения необходимо задать интервал [a, b], на котором будет происходить поиск решения. Если решение действительно существует, является на этом интервале единственным , принадлежит заданному интервалу и функция F(x) принимает на границах интервала значения противоположных знаков. Другими словами, произведение значений функции на границах интервала отрицательно: F(a)F(b) < 0. Далее исходный интервал делится средней точкой с = (а+b)/2 на две равные части, из которых выбирается лишь та, которая содержит решение уравнения. Процедура деления отрезка пополам повторяется до тех пор, пока корень функции не будет найден с заданной точностью. Оценкой погрешности в данном случае может быть величина последнего интервала |а-b| или значение |F(x)|.
Исходные данные в этой задаче – это коэффициенты уравнения, точность решения и отрезок [a,b], на котором ищется решение уравнения.
Под внутренней формой будем понимать организацию данных в оперативной памяти. При этом будем использовать два типа этой организации – явного отображения посредством окна вывода сообщений и неявного размещения в памяти в форме простых переменных.
Реклама

Результат этой задачи, т.е. корень будем отображать сразу в этом окне вывода сразу после его нахождения.
Вычислительный процесс этой задачи базируется на координатах отрезка[a,b] , точности e вещественного типа и функцие 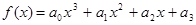 .
.
Исключительные ситуации могут возникнуть тогда, когда введены коэффициенты уравнения, при которых нет действительных корней. При возникновении этой ситуации программа прекращает работу, выводит сообщение о том, что у этого уравнения нет действительных корней. Также исключительная ситуация возникает тогда, когда отрезок, на котором ищется решение уравнения не имеет корней или имеет два корня. В этом случае программа прекращает работу и выводит сообщение о том, что неправильно задан отрезок. Для того, чтобы правильно задать отрезок программа выводит корни этого уравнения, найденные методом решения квадратных уравнений.
2.4 Модульная организация программы
Решение поставленной задачи представляет форму программной реализации алгоритма как цельная программа и функция, к которой обращается главная программа.
При рекурсивной организации программы имеем стандартный модуль, но содержащий функцию funct
.
Функция funct
типа real
. Функция возвращает значения. Все переменные в программе глобальные. Значения коэффициентов передаются в функцию.
Исходные данные:
a0, a1, a2 – коэффициенты уравнения типа Real;
e – точность решения типа Real;
a, b – координаты отрезка типа Real.
Результирующие данные:
x – переменная хранящая значение точки(I итерация, корень) типа Real;
i – счетчик итераций типа Integer.
Промежуточные данные:
x_pre - переменная, хранящая предыдущее значение точки (i-1 итерация) типа Real;
d– дискриминант типа Real;
x1 –первый корень уравнения, найденный методом решения квадратных уравнений через дискриминант типа Real;
x2 - второй корень уравнения, найденный методом решения квадратных уравнений через дискриминант типа Real;
Вычислительный процесс базируется на следующем подходе. Проверяем есть ли у заданного уравнения действительные корни по формуле: D=a1^2-a0*a2. Если D<0, значит действительных корней нет и решить такую систему у нас не получится. Если действительные корни есть, то найдем их методом решения квадратных уравнений через дискриминант. Проверим единственность корня на заданном отрезке [a,b]. Если на этом отрезке существует не один корень или вообще не существует корней, то надо задать другой отрезок. Затем делим отрезок пополам и проверяем на какой его половине лежит корень. Для этого значение функции должна быть разного знака на концах отрезка. Полученный отрезок мы опять делим пополам. Этот итерационный процесс мы продолжаем до тех пор пока модуль разности между точкой, полученной на i-й итерации и точкой, полученной на (i-1) итерации не будет меньше заданной точности. Это и будет корнем уравнения.
Реклама

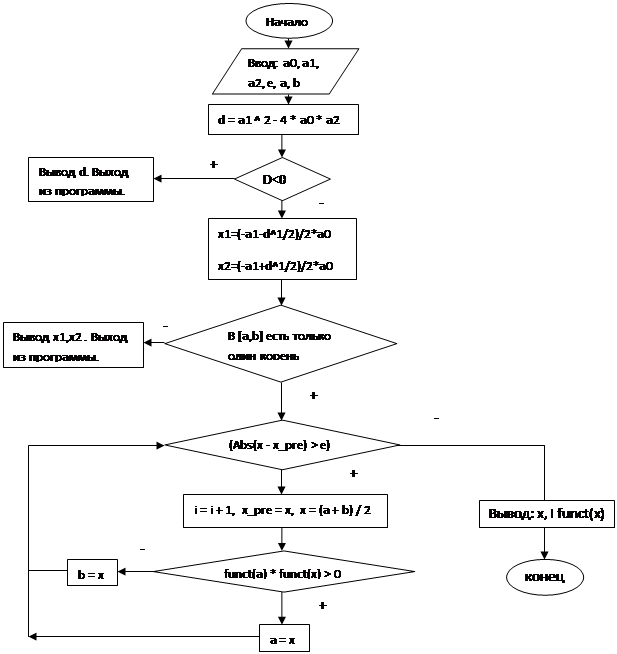
Блок-схема решения задачи представлена ниже
4 Создание программы на алгоритмическом языке
Для реализации программы решения поставленной задачи использован алгоритмический язык VBA, возможности которого достаточны для реализации задач подобного типа. Для отображения результатов (корни уравнения) использовано Windows-окно для вывода сообщений. Результат, выводимый через это окно, сохраняется только на время его существования. Ниже представлен листинг варианта программы, разработанный согласно представленной расчетной схемы и графическому алгоритму.
Private a0, a1, a2, e, a, b, x, i
Private Sub CommandButton1_Click()
a0 = CDbl(TextBox2.Text)
a1 = CDbl(TextBox3.Text)
a2 = CDbl(TextBox4.Text)
e = CDbl(TextBox5.Text)
a = CDbl(TextBox9.Text)
b = CDbl(TextBox10.Text)
d = a1 ^ 2 - 4 * a0 * a2
TextBox14.Text = d
If d < 0 Then
Label16.Visible = True
TextBox7.Text = ""
TextBox8.Text = ""
TextBox11.Text = ""
TextBox12.Text = ""
TextBox13.Text = ""
Exit Sub
Else
Label16.Visible = False
End If
x1 = (-a1 - d ^ (1 / 2)) / 2 * a0
x2 = (-a1 + d ^ (1 / 2)) / 2 * a0
TextBox12.Text = x1
TextBox13.Text = x2
t = 0
If (a < x1) And (a < x2) And (b > x1) And (b > x2) Then t = 1
If (a < x1) And (a < x2) And (b < x1) And (b < x2) Then t = 1
If (a > x1) And (a > x2) And (b > x1) And (b > x2) Then t = 1
If (a > x1) And (a < x2) And (b > x1) And (b < x2) Then t = 1
If t = 1 Then
Label14.Visible = True
TextBox7.Text = ""
TextBox8.Text = ""
TextBox11.Text = ""
Exit Sub
Else
Label14.Visible = False
Label16.Visible = False
i = 0
x = a
Do
i = i + 1
x_pre = x
x = (a + b) / 2
If funct(a) * funct(x) > 0 Then
a = x
Else
b = x
End If
Loop While (Abs(x - x_pre) > e)
TextBox7.Text = x
TextBox8.Text = i
TextBox11.Text = funct(x)
End If
End Sub
Private Sub CommandButton3_Click()
UserForm1.Hide
End Sub
Function funct(x)
funct = a0 * x ^ 2 + a1 * x + a2
End Function
В программе всегда выводятся корни, полученные методом решения квадратного уравнения, чтобы сравнить их с полученными результатами, найденными при помощи метода деления отрезка пополам. В ходе тестирования программы ошибок выявлено не было. Результаты всегда находятся с точность до заданного ε.
|