Вариант 3.
1. Решите уравнение 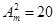
Решение
По определению
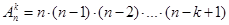 . .
Тогда 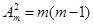 и уравнение принимает вид и уравнение принимает вид 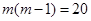 или или 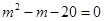 откуда получаем откуда получаем 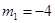 и и 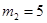
Так как m может быть только натуральным числом, то значение 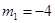 отбрасываем. отбрасываем.
Ответ:
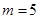 . .
2. В урне находится 12 белых и 8 черных шаров. Найти вероятность того, что два одновременно изъятых наудачу шара будут черными
Решение
При выборе двух шаров из 20 существует 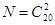 различных вариантов, где различных вариантов, где 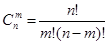 , тогда , тогда
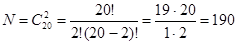
Определим благоприятных исходов, т.е. извлечены два черных шара. Два черных шара из 8 можно выбрать 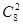 способами следовательно, число благоприятных исходов способами следовательно, число благоприятных исходов
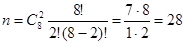 . .
Искомая вероятность, согласно классическому определению вероятности, равна отношению числа благоприятных исходов к числу всех исходов:
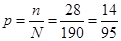 . .
Ответ:
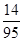 . .
3. Найдите вероятность того, что наудачу взятое двузначное число окажется кратным либо 4, либо 5, либо тому и другому
Решение
Воспользуемся классическим определением вероятности. Двузначные числа начинаются с 10 и заканчиваются 99 и всего их 90, т.е. N= 90. Теперь посчитаем, сколько у нас чисел кратных либо 4, либо 5, либо тому и другому.
Число кратное 4-м имеет вид 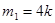 , кратное 5 , кратное 5 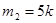 , кратное 4 и 5 , кратное 4 и 5 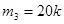 . .
В интервале от 10 до 99 всего 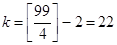 числа кратных четырем (2 кратных до десяти), числа кратных четырем (2 кратных до десяти), 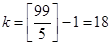 чисел кратных пяти (1 кратное до 10) и чисел кратных пяти (1 кратное до 10) и 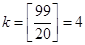 числа кратных и четырем и пяти. числа кратных и четырем и пяти.
Так как множество чисел кратных 4 и множество чисел кратных 5 не пересекаются, то всего получается 22 + 18 = 40 чисел удовлетворяющих необходимому нам условию, причем числа кратные и четырем и пяти уже входят в эти 40 чисел. В итоге получаем, что вероятность того, что наудачу взятое двузначное число окажется кратным либо 4, либо 5, либо тому и другому равна 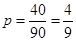 . .
Ответ:
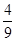 . .
4. В партии 10 деталей, из которых 8 стандартные. Из этой коробки наудачу извлекается 2 детали. Х – число стандартных деталей. Найти закон распределения, функцию распределения дискретной случайной величины Х, а также основные числовые характеристики
Решение
Среди 2-х извлеченных деталей может быть 0, 1 или 2 стандартные.
Найдем вероятность каждого исхода.
0 стандартных: 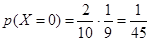
1 стандартная: 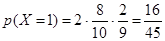
2 стандартных: 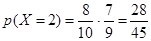
Закон распределения принимает вид:
Запишем функцию распределения полученной случайной величины Х:
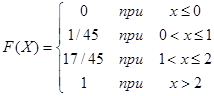
Математическое ожидание М(Х) дискретной случайной величины находится по формуле:
Реклама

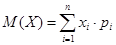 , и подставляя данные, получим: , и подставляя данные, получим:
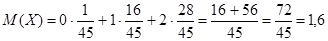
Дисперсию дискретной случайной величины можно вычислить по формуле:
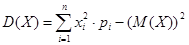 , и, подставляя данные, получим: , и, подставляя данные, получим:
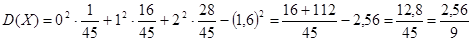
Среднеквадратичное отклонение:
s(Х)=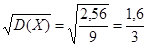
Ответ:
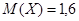 ; ; 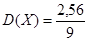 ; ; 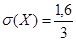 . .
5. По данной выборке постройте полигон. Найти эмпирическую функцию.
Решение
Построим полигон частот – ломаную, соединяющую точки с координатами (Хi
; Ni
).
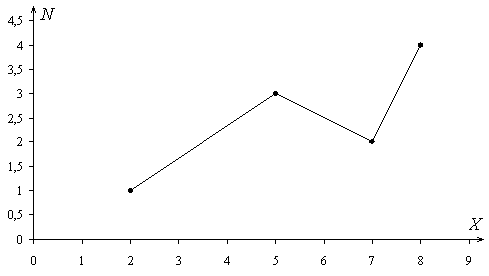
Объем выборки равен N = 1 + 3 + 2 + 4 = 10.
Найдем относительные частоты и составим эмпирическую функцию распределения:
| Хi
|
2 |
5 |
7 |
8 |
| wi
|
0,1 |
0,3 |
0,2 |
0,4 |
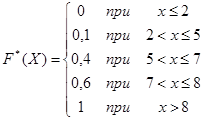
Ответ:
решение выше.
|