Государственное образовательное учреждение
высшего профессионального образования
«Забайкальский государственный гуманитарно-педагогический
университет им. Н.Г. Чернышевского» (ЗабГГПУ)
Факультет физико-математический
Кафедра фундаментальной и прикладной математики,
теории и методики обучения математики
Курсовая работа
Тема: Методика обучения учащихся исследованию функций с помощью производной
Выполнила: студентка 141 группы
Просолова В. Ю.
Проверил: доцент кафедры
ФиПМТиМОМ
к.п.н. Тонких Г.Д.
Чита, 2010 г.
Оглавление
Введение…………………………………………………………………..3
§1. Методика обучения учащихся исследованию функций на монотонность и нахождение экстремумов……………………………………………...5
§2. Применение общей схемы к исследованию функций……………14
§3. Типичные ошибки учащихся при исследовании функций………………………………………………………………………………19
§4. План-конспект урока по теме: «Применение производной к исследованию функций»…………………………………………………………......24
Заключение………………………………………………………………26
Список используемой литературы…………………………………......27
Введение
Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решить многие задачи и парой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес.
Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Развитие математики со времён Древнего Египта, Вавилона, Греции прошло не малый путь, меняясь и преобразовываясь.
При изучении процессов реального мира (физических, химических, биологических, экономических и всевозможных других) мы постоянно встречаемся с характеризующими их величинами, меняющимися в течение рассматриваемых процессов. При этом часто бывает, что изменению одной величины сопутствует и изменение другой или даже, более того, изменение одной величины является причиной изменения другой. Взаимосвязные изменения числовых характеристик рассматриваемых величин приводят к их функциональной зависимости в соответствующих математических моделях. Поэтому понятие функции является одним из самых важных понятий в математике и ее приложениях.
Реклама

Школьный курс характеризуется содержательным раскрытием понятий, утверждений и методов, относящихся к началам анализа, выявлением их практической значимости. При изучении вопросов анализа широко используются наглядные соображения: уровень строгости изложения определяется с учётом общеобразовательной направленности изучения начал анализа и согласуется с уровнем строгости приложений изучаемого материала в смежных дисциплинах [5].
Цель изучения курса алгебры и начала анализа в 10-11 классах систематическое изучение функций как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций, подготовки необходимого апорта для изучения геометрии и физики.
Цель: рассмотреть методические особенности обучения учащихся исследованию функций с помощью производной
Задачи:
- рассмотреть методику обучения учащихся исследованию функций на монотонность и нахождение экстремумов
- показать применение общей схемы к исследованию функций
- рассмотреть типичные ошибки учащихся при исследовании функций
- показать план-конспект урока по теме: «Применение производной к исследованию функций»
Объект исследования: процесс обучения курсу «Алгебра и начала анализа».
Предмет исследования: методика обучения учащихся исследованию функций.
Методы исследования: анализ научно-методической литературы; изучение нормативных документов.
§1.
Методика обучения учащихся исследованию функций с помощью производной на монотонность и нахождение экстремумов
В соответствии со стандартом среднего (полного) общего образования по математике раздел «Функции» включает следующие вопросы:
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
Учащиеся должны уметь:
· определять значение функции по значению аргумента при различных способах задания функции;
· строить графики изученных функций;
· описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
Реклама

· решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
· использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
· вычислять производные элементарных функций, используя справочные материалы;
· исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа [10].
Применение производной к исследованию функций, построению графиков, решению задач на нахождение наибольших и наименьших значений – важнейший раздел темы «Производная и ее применение». Материал этой темы используется при изучении многих классов функций: тригонометрических, показательной, логарифмической и др. Он имеет также очень большое прикладное значение и играет большую роль в установлении межпредметных связей (в особенности с курсом физики).
Приведем тематическое планирование раздела: «Применения производной» в соответствии с учебником Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений/ А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др. [8].
Тематическое планирование
№
урока
|
Содержание учебного материала |
| 1,2 |
Касательная к графику функции. Уравнение касательной |
| 3,4 |
Производная в физике и технике. Механический смысл производной |
| 5-7 |
Признак возрастания (убывания) функции |
| 8-10 |
Критические точки функции, максимумы и минимумы |
| 11-13 |
Примеры применения производной к исследованию функции |
| 14-16 |
Наибольшее и наименьшее значения функции |
| 17 |
Контрольная работа |
Изучение темы «Применение производной к исследованию функций» требует знания некоторых определений и теорем, которые изучались ранее. Эти сведения следует повторить до изучения темы: понятия возрастания и убывания функции на множестве, определение производной, ее геометрический смысл, в связи с этим – понятия касательной, углового коэффициента прямой, условие параллельных прямых.
В ходе решения задач ученикам понадобится находить производные функций, пользоваться известными графиками для построения графиков других функций. Повторить нужно и метод интервалов. Наконец, для усвоения понятия экстремума функции и доказательства соответствующих теорем надо вспомнить определение предела функции. Поскольку в дальнейшем обучении будет идти речь о необходимых и достаточных условиях, и эти понятия должны быть усвоены учащимися [7].
Признак возрастания (убывания) функции
.
Одно из основных применений производной в школьном курсе алгебры и начал анализа − это исследование функций, в частности нахождение промежутков возрастания и убывания. Программой по математике сформулированы требования к усвоению этого материала − учащиеся должны уметь находить промежутки возрастания (убывания) функций.
Для подготовки к сознательному усвоению формулируемого в теме достаточного признака возрастания (убывания) функции (до его введения) полезно рассмотреть учащимся геометрические иллюстрации, на которых показаны графики функций, имеющих разный характер изменения, а также касательные в точках, принадлежащих к промежуткам возрастания и промежуткам убывания функций. Анализируя расположение касательных по отношению к оси абсцисс (угол наклона) и определяя тем самым знаки значений производной, учащиеся подводятся к самостоятельному формулированию требуемых признаков [1].
Достаточный признак возрастания функции
. Если 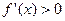 в каждой точке интервала в каждой точке интервала 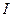 , то функция , то функция 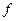 возрастает на возрастает на 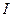 . .
Достаточный признак убывания функции.
Если 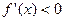 в каждой точке интервала в каждой точке интервала 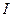 , то функция , то функция 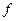 убывает на убывает на 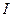 . .
Доказательство этих признаков проводится на основании формулы Лагранжа.
Учащимся необходимо разъяснить наглядный смысл признаков, который приводится из физических рассуждений.
Пусть движущаяся по оси ординат точка в момент времени 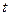 имеет ординату имеет ординату 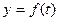 . Тогда скорость этой точки в момент времени . Тогда скорость этой точки в момент времени 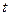 равна равна 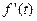 . Если . Если 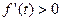 в каждый момент времени из промежутка в каждый момент времени из промежутка 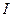 , то точка движется в положительном направлении оси ординат, т. е. если , то точка движется в положительном направлении оси ординат, т. е. если 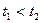 , то , то  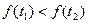 . Это означает, что функция . Это означает, что функция 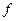 возрастает на промежутке возрастает на промежутке 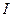 [2]. [2].
Пример.
Найти промежутки возрастания и убывания функции.
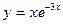
Решение: найдем производную функции (заметим, что она существует для всех 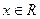 ): ):
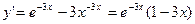 . .
Приравняем производную к нулю: 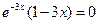 , откуда , откуда 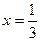 . .
При 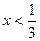 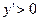 , следовательно, при , следовательно, при 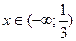 , функция возрастает, а при , функция возрастает, а при 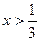 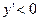 , следовательно, при , следовательно, при 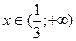 , функция убывает [3]. , функция убывает [3].
После рассмотрения темы на возрастание (убывание) функции, вводится понятие критической точки или экстремумов функции.
Критические точки функции, ее максимумы и минимумы.
Теоретический материал этой темы составляет основу получения общего метода решения большого класса задач − задач на нахождение экстремумов функций. На этапе, где рассматривается общая схема исследования функции, у учащихся еще не было метода нахождения точек экстремума. В данной теме рассматривается необходимый признак экстремума (Теорема Ферма) и достаточный признак максимума и минимума. После изучения темы каждый учащийся должен уметь находить экстремумы функций.
1. Для активного восприятия учащимся нового материала целесообразно повторить понятие точек экстремума и понятие экстремума.
2. Используя таблицу с рисунками (графиками функций), с помощью системы наводящих вопросов можно подвести учащихся к самостоятельному формулированию (к упрощенной формулировке) признаков максимума и минимума функции:
1) Укажите точки максимума и минимума функции.
2) Определите знак значений производной функции в промежутке слева от точки максимума (минимума).
3) Определите знак значений производной функции в промежутке справа от точки максимума (минимума).
4) Как меняется знак производной при прохождении через точку максимума (минимума)?
Доказательство признаков максимума и минимума функции необходимо проводить с привлечением учащихся [1].
Рассмотрим определение критической точки:
Определение.
Внутренние точки области определения функции, в которых она равна нулю или не существует, называют критическими точками этой функции.
Эти точки играют важную роль при построении графика функции, поскольку только они могут быть точками экстремума функции. Рассмотрим соответствующее утверждение, его называют теоремой Ферма.
Необходимое условие экстремума.
Если точка 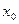 является точкой экстремума функции является точкой экстремума функции 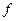 , то она равна нулю: , то она равна нулю: 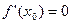 . .
Важно отметить, что теорема Ферма лишь необходимое условие экстремума: из того, что производная в точке 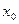 обращается в нуль, необязательно следует, что в этой точке функция имеет экстремум. Например, производная функции обращается в нуль, необязательно следует, что в этой точке функция имеет экстремум. Например, производная функции 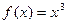 обращается в нуль в точке 0, но экстремума в этой точке не имеет. обращается в нуль в точке 0, но экстремума в этой точке не имеет.
Рассмотрим теперь критические точки, в которых производная не существует.
Пример 1.
Рассмотрим функцию 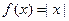 . Эта функция не имеет производной в точке 0. Значит, 0 − критическая точка. Очевидно, что в точке 0 функция имеет минимум. . Эта функция не имеет производной в точке 0. Значит, 0 − критическая точка. Очевидно, что в точке 0 функция имеет минимум.
Пример 2.
Точка 0 для функции 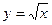 не является критической: в ней производная не существует, но она не внутренняя точка области определения. не является критической: в ней производная не существует, но она не внутренняя точка области определения.
Из теоремы Ферма следует, что при нахождении точек экстремумов функции требуется в первую очередь найти ее критические точки. Но как видно из рассмотренных примеров, вопрос о том, действительно ли данная критическая точка есть точка экстремума, требует дополнительного исследования. При этом часто помогают такие достаточные условия существования экстремума в точке.
Признак максимума функции.
Если функция 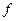 непрерывна в точке непрерывна в точке 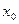 , а , а 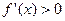 на интервале на интервале 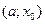 и и 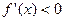 на интервале на интервале 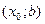 , то точка , то точка 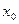 является точкой максимума функции является точкой максимума функции 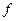 . .
Учащимся удобно пользоваться упрощенной формулировкой этого признака: если в точке 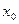 производная меняет знак с плюса на минус, то производная меняет знак с плюса на минус, то 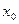 есть точка максимума. есть точка максимума.
Признак минимума функции.
Если функция 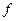 непрерывна в точке непрерывна в точке 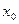 , , 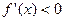 на интервале на интервале 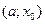 и и 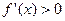 на интервале на интервале 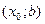 , то точка , то точка 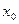 является точкой минимума функции является точкой минимума функции 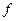 . .
Удобно пользоваться упрощенной формулировкой этого признака: если в точке 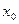 производная меняет знак с минуса на плюс, то производная меняет знак с минуса на плюс, то 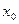 есть точка минимума [2]. есть точка минимума [2].
Пример.
Найти экстремумы функции 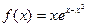 . .
Решение: область определения заданной функции есть множество всех действительных чисел. Найдем критические точки функции, для чего решим уравнение 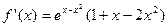 . .
Так как  , то имеем , то имеем 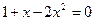 , откуда , откуда 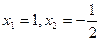 . .
Исследуем знак производной функции на всех промежутках, на которые стационарные точки разбили множество 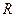 . При . При 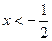 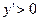 , при , при 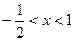 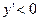 , а при , а при 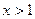 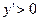 . Итак, . Итак, 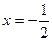 - точка максимума функции, а - точка максимума функции, а 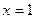 - точка минимума функции. - точка минимума функции.
С учащимися необходимо рассмотреть тему на наибольшее и наименьшее значение функции, обращая особое внимание на тот факт, что наибольшее (наименьшее) значение функции не является максимумом (минимумом) функции.
Наибольшее и наименьшее значения функции.
Решение многих практических задач часто сводится к нахождению наибольшего и наименьшего значений непрерывной на отрезке функции. В курсах анализа доказывается теорема Вейерштрасса, утверждающая, что непрерывная на отрезке 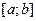 функция функция 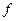 принимает на этом отрезке наибольшее и наименьшее значение, т. е. существуют точки отрезка принимает на этом отрезке наибольшее и наименьшее значение, т. е. существуют точки отрезка 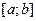 , в которых , в которых 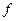 принимает наибольшее и наименьшее на принимает наибольшее и наименьшее на 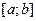 значения. значения.
Чтобы найти наибольшее и наименьшее значение функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее[2].
Пример.
Найти наибольшее и наименьшее значение функции 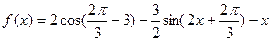 на отрезке на отрезке 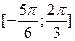 . .
Решение: запишем выражение для функции в более удобном виде, воспользовавшись для этого свойством четности функции косинуса 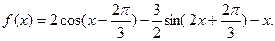
Найдем 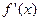
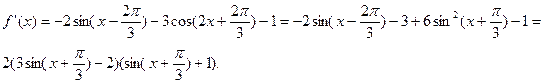
Найдем значения аргумента, при которых 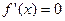 , для чего решим уравнения , для чего решим уравнения 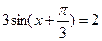 и
и 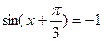 . Имеем следующую совокупность решений . Имеем следующую совокупность решений
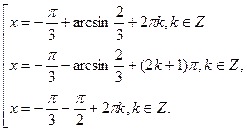
Отрезку 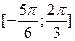 принадлежит только три решения уравнения принадлежит только три решения уравнения 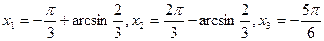 . .
Действительно, длина заданного в условии задачи отрезка меньше 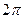 , то есть меньше разности каждой из трех арифметических прогрессий, записанной выше совокупности решений, поэтому рассматриваемому отрезку принадлежит не более одного числа каждого семейства. , то есть меньше разности каждой из трех арифметических прогрессий, записанной выше совокупности решений, поэтому рассматриваемому отрезку принадлежит не более одного числа каждого семейства.
Так как функция 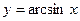 возрастает на своей области определения, то возрастает на своей области определения, то  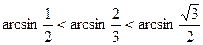 , то есть , то есть 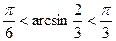 , откуда следует, что , откуда следует, что 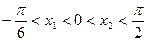 . То есть отрезку . То есть отрезку 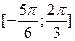 принадлежат принадлежат 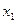 и и 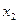 . .
Находя значения 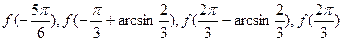 и сравнив их , находим, что на отрезке и сравнив их , находим, что на отрезке 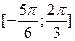 функции функции 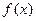 имеет наибольшее значение имеет наибольшее значение 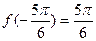 , а наименьшее значение , а наименьшее значение 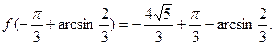
§2. Применение общей схемы к исследованию функций
Теоретический материал, который требуется для изучения исследований функций с помощью производной уже известен учащимся. В данной теме фактически систематизируются знания учащихся, относящиеся к вопросам нахождения промежутков возрастания (убывания) и экстремумов, показывается общий метод получения результатов. Таким образом, изучение этой темы завершает рассмотрение теоретических вопросов, связанных с исследованием функций. Все положения, которые нужно отразить в решении задания на исследование, имеют теоретические обоснования, общие методы решения.
В ходе изучения этой темы учащиеся должны научиться проводить исследование функций по общей схеме и строить их графики. Построения графика функции необходимо начинать с исследования функции, которое состоит в том, что для данной функции:
1) находят ее область определения;
2) выясняют, является ли функция 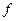 четной или нечетной, является ли периодической; четной или нечетной, является ли периодической;
3) точки пересечения графика с осями координат;
4) промежутки знакопостоянства;
5) промежутки возрастания и убывания;
6) точки экстремума и значения 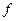 в этих точках; в этих точках;
7) исследуют поведение функции в окрестности «особых» точек и при больших по модулю 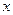 ; ;
На основании такого исследования строится график функции.
Исследование функции на возрастание (убывание) и на экстремум удобно проводить с помощью производной. Для этого сначала находят производную функции 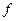 и ее критические точки, а затем выясняют, какие из них являются точками экстремума. и ее критические точки, а затем выясняют, какие из них являются точками экстремума.
Пример 1.
Исследуем функцию 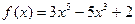 и построим ее график. и построим ее график.
Проведем исследование по указанной схеме.
1) 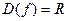 , так как , так как 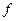 - многочлен. - многочлен.
2) Функция 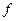 не является ни четной, ни нечетной не является ни четной, ни нечетной
3) График 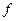 пересекается с осью ординат в точке пересекается с осью ординат в точке 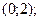 чтобы найти точки пересечения с осью абсцисс, надо решить уравнение чтобы найти точки пересечения с осью абсцисс, надо решить уравнение 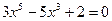 , один из корней легко найти , один из корней легко найти 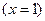 . Другие корни (если они есть) могут быть найдены только приближенно. Промежутки знакопостоянства не находим. . Другие корни (если они есть) могут быть найдены только приближенно. Промежутки знакопостоянства не находим.
4) Найдем производную функции 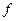 : :
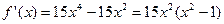
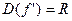 , поэтому критических точек, для которых , поэтому критических точек, для которых 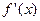 не существует, нет. не существует, нет.
Заметим, что 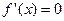 , если , если 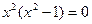 , т.е. при значениях аргумента, равных 0,-1 и 1. Рассматриваемая функция имеет три критические точки. , т.е. при значениях аргумента, равных 0,-1 и 1. Рассматриваемая функция имеет три критические точки.
Составляем таблицу:
В первой строке этой таблицы указаны в порядке возрастания критические точки функции и ограниченные ими промежутки. В третьей строке записаны выводы о ходе изменения данной функции. Критическая точка равная 0 функции 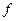 не является точкой экстремума [2]. не является точкой экстремума [2].
Строим график функции (рис.1). Строить его удобно по промежуткам, которые указаны в таблице.
Пример 2.
Исследовать функцию 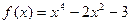
1) 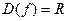
2) Функция четная, исследование ее можно проводить на промежутке 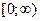 . .
3) Найдем точки пересечения графика функции с осями координат, т.е. решим уравнение 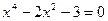 . Пусть . Пусть 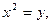 тогда уравнение примет вид: тогда уравнение примет вид: 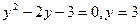 или или 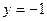 , т.е. , т.е. 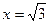 или или 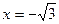 , , 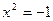 не имеет решения. Получили две точки пересечения с осью абсцисс не имеет решения. Получили две точки пересечения с осью абсцисс 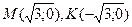 . График пересекает ось ординат в точке . График пересекает ось ординат в точке 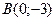 . .
4) Найдем производную функции 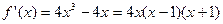
5) Найдем критические точки функции:
а) 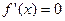 , если , если 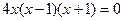 , ,  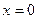 , или , или 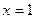 , или , или 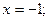
б) 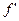 определена на всей определена на всей 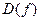
6) Определим знак производной на промежутках, найдем значения в точках -1, 0, 1. Полученные данные занесем в таблицу и построим график [2].
Построим график данной функции (рис. 2):
Приведем примеры заданий для самостоятельной работы по исследованию функций.
Исследуйте функцию и постройте ее график:
1) 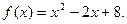
2) 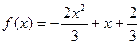
3) 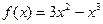
4) 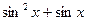
5) 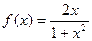
После изучения данной темы учащимся предлагается контрольная работа.
Контрольная работа по теме «Производная и ее применение»
I вариант
1. Дана функция 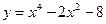 . Найдите: . Найдите:
а) промежутки возрастания и убывания функции;
б) точки экстремума;
в) наибольшее и наименьшее значения функции на отрезке 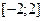 . .
2. Постройте график функции 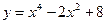 . .
3. Составьте уравнение касательной к графику функции 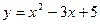 в точке с абсциссой в точке с абсциссой 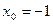 . .
4. В какой точке касательная к графику функции 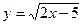 параллельна прямой параллельна прямой 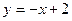 ? ?
5. Найдите наибольшее и наименьшее значения функции 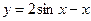 на отрезке на отрезке 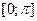 . .
II вариант
1. Дана функция 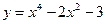 . Найдите: . Найдите:
а) промежутки возрастания и убывания функции;
б) точки экстремума;
в) наибольшее и наименьшее значения функции на отрезке 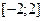 . .
2. Постройте график функции 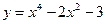 . .
3. Составьте уравнение касательной к графику функции 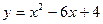 в точке с абсциссой в точке с абсциссой 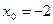 . .
4. В какой точке касательная к графику функции 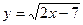 параллельна прямой параллельна прямой 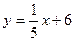 ? ?
5. Найдите наибольшее и наименьшее значения функции 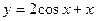 на отрезке на отрезке 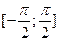 [10]. [10].
§3. Типичные ошибки учащихся при исследовании функций
При проведении исследования функций учащиеся часто допускают ошибки. Большое число ошибок допускается при построении графиков функции с использованием производной.
а) Пусть требуется исследовать с помощью производной функцию 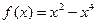 и построить ее график. Результаты исследования функции оформим в виде таблицы (таб. 1). и построить ее график. Результаты исследования функции оформим в виде таблицы (таб. 1).
Таблица 1
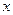 |
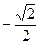 |
0 |
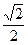 |
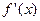 |
+ |
0 |
− |
0 |
+ |
− |
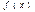 |
 |
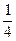 |
 |
0 |
 |
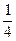 |
 |
| Max |
min |
max |
Покажем ошибочные эскизы графиков, которые учащиеся изображают по данной таблице (рис. 3,4,5,6)
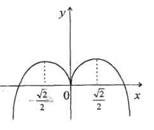 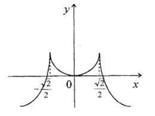 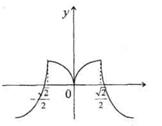
На каждом из этих рисунков допущены грубые математические ошибки и происходят они из-за того, что учащиеся используют из таблицы лишь сведения о том, где функция возрастает и где убывает, и совершенно не берут во внимание существование производной функции в критических точках. В таблице 1 отмечено, что в точках, 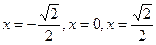 производная функции существует, а это означает, что в точках с этими абсциссами можно провести касательную. Тот факт, что производная функции в этих точках равна нулю, означает, что в точках с этими абсциссами касательные к кривой должны быть параллельны оси Ox
. Анализ рисунков 3,4,5,6 показывает, что указанное выше требование нарушено, а именно, на рисунке 3 нельзя провести касательную к кривой с абсциссой производная функции существует, а это означает, что в точках с этими абсциссами можно провести касательную. Тот факт, что производная функции в этих точках равна нулю, означает, что в точках с этими абсциссами касательные к кривой должны быть параллельны оси Ox
. Анализ рисунков 3,4,5,6 показывает, что указанное выше требование нарушено, а именно, на рисунке 3 нельзя провести касательную к кривой с абсциссой 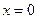 ; на рисунках 4 и 5 – в точках с абсциссами ; на рисунках 4 и 5 – в точках с абсциссами 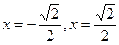 ; на рисунке 6 – в точках с абсциссами ; на рисунке 6 – в точках с абсциссами 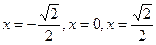 . .
Правильный график функции 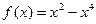 показан на рисунке 7. показан на рисунке 7.
б) При исследовании функции на монотонность учащиеся очень часто не учитывают точек, в которых функция неопределенна. Приведем пример такой ошибки.
Исследовать функцию 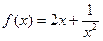 на монотонность. на монотонность.
Часто учащиеся поступают так: 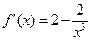 ; находят точки, в которых производная равна нулю: ; находят точки, в которых производная равна нулю: 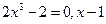 ; затем, множество всех действительных чисел разбивают точкой ; затем, множество всех действительных чисел разбивают точкой 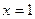 на два промежутка на два промежутка 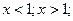 находят знаки производной на каждом промежутке и делают затем ошибочный вывод о монотонности функции на каждом из этих двух промежутков. находят знаки производной на каждом промежутке и делают затем ошибочный вывод о монотонности функции на каждом из этих двух промежутков.
Поступать же надо было так. Множество всех действительных чисел следовало бы разбить на промежутки точками, в которых функция не определена и точками в которых производная равна либо нулю, либо равна бесконечности, либо не существует. В данном случае мы получим три промежутка: 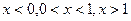 . Знак производной функции на каждом из них отмечен на рисунке 8. . Знак производной функции на каждом из них отмечен на рисунке 8.
Ответ должен быть записан в следующем виде:
на промежутке 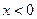 функция возрастает; функция возрастает;
на промежутке 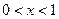 функция убывает; функция убывает;
на промежутке 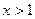 функция возрастает. функция возрастает.
По поводу записи ответа отметим следующее: если функция 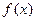 непрерывна в каком-либо из концов промежутка возрастания (убывания), то его можно присоединить к этому промежутку. Так, в нашем случае, в точке непрерывна в каком-либо из концов промежутка возрастания (убывания), то его можно присоединить к этому промежутку. Так, в нашем случае, в точке 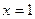 функция непрерывна, а значит промежутки могли бы быть записаны так: функция непрерывна, а значит промежутки могли бы быть записаны так: 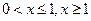 . .
в) Ряд ошибок связан с решением текстовых задач на экстремум. Проанализируем эти ошибки.
Очень часто учащиеся в процессе решения задач на экстремум при исследовании полученной функции на наибольшее (наименьшее) значение делают такой вывод: «Функция на промежутке имеет один максимум, тогда максимальное значение и будет наибольшим». Такое утверждение содержит ошибки, разберем суть этих ошибок.
На рисунке 9 показан график такой функции, которая на промежутке 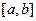 имеет одну точку максимума, но максимальное значение не является имеет одну точку максимума, но максимальное значение не является наибольшим; наибольшее значение функция достигает в точке 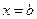 . .
Учащиеся были бы почти правы, если бы они записали вывод в таком виде: «Функция на промежутке имеет один экстремум, который максимум, тогда максимальное значение будет и наибольшим на данном промежутке». Этому утверждению соответствует рисунок 10.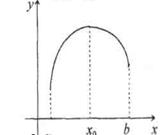
Но и последнее утверждение содержит ошибку. На рисунке 9 показан график функции, которая на отрезке 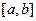 имеет одну точку экстремума, которая является точкой максимума, но максимальное значение не является на этом промежутке наибольшим; наибольшее значение достигается при имеет одну точку экстремума, которая является точкой максимума, но максимальное значение не является на этом промежутке наибольшим; наибольшее значение достигается при 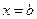 . .
Обобщая проведенные рассуждения, вывод, сделанный учащимися, должен быть таким: «Непрерывная
функция имеет на промежутке одну точку экстремума
, которая является точкой максимума, тогда это максимальное значение и будет наибольшим на указанном промежутке».
Приведенных в работе примеров типичных ошибок, допускаемых учащимися при изучении Алгебры и начал анализа, вполне достаточно, чтобы показать учителю насколько важно учить учеников, а им самим учиться, рефлексивно- оценочной деятельности, которая позволит устранить и предупредить подобного рода ошибки [5].
§4. План-конспект урока по теме «Производная и ее применение»
Цель урока:
обобщить и систематизировать знания и умения учащихся по теме «Производная и ее применение».
Тип урока:
обобщения и систематизация знаний
Структура урока:
1. Постановка цели урока.
2. Актуализация опорных знаний и умений.
3. Самостоятельная работа.
4. Подведение итогов работы на уроке.
Оборудование урока:
1. Рисунки. 2. Кодоскоп. Кодопозитивы.
Выбор методов обучения.
Основные методы − эвристические и репродуктивные.
Ход урока:
1. Постановка цели урока.
Учитель сообщает учащимся цель урока.
2. Актуализация опорных знаний и умений.
На данном этапе урока учащиеся сидят по группам, соответствующим ими выбранной тематике домашнего задания (количество учащихся в группе корректируется учителем по 5-6 человек). Столы стоят таким образом, чтобы учащиеся могли видеть доску. Четыре представителя от каждой группы излагают у доски одну из задач, подобранных из различных пособий, и отвечают на вопросы:
1. Геометрический смысл производной.
2. Физический смысл производной.
3. Роль знака производной для определения возрастания или убывания функции на некотором промежутке.
4. Дать определение (в широком смысле) касательной, проведенной к графику данной функции через точку 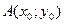 . Записать уравнение касательной. . Записать уравнение касательной.
Пока они готовятся, все учащиеся слушают историческую справку, делая соответствующие записи в тетрадях.
Заслушав план решения каждой задачи, записанной на доске, учащиеся делают вывод о том, что наиболее емкое применение производная находит при решении различных задач и построении графиков функций.
3. Самостоятельная работа.
Учащимся дается задание: «Исследовать функцию 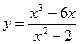 и построить ее график» и построить ее график»
При фронтальной беседе с группами вырисовывается алгоритм решения задачи и чертеж к ней.
4.Урок заканчивается подведением итогов Учащимся дается домашнее задание: найти в дополнительной литературе задачи на применение производной в других науках.
Заключение
В курсовой работе рассмотрена методика обучения учащихся исследованию функций с помощью производной. Нами выполнен анализ содержания стандарта среднего (полного) общего образования по математике, учебника Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений/ А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.. с точки зрения изучения функций и их исследования с помощью производной
В работе показано применение общей схемы к исследованию функций, разработаны задания для самостоятельной работы, контрольная работа.
Нами проанализированы типичные ошибки учащихся при исследовании функций и построении графиков. В курсовой работе представлен план-конспект урока по теме: «Применение производной к исследованию функций»
Список используемой литературы
1. Алгебра и начала анализа в 9-10 классах: Пособие для учителя / Л. О. Денищева, Ю. П. Дудницын, Б. М. Ивлев и др. − М.: Просвещение, 1988. – 272с.
2. Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений/ А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова. − 7-е изд., доп. − М.: Просвещение, 1998. − 365с.
3. Далингер В. А. Начала математического анализа. − Омск: ООО «Издательство-Полиграфист», 2002.-158с.
4. Далингер В.А. Методика обучения учащихся элементам математического анализа: Учебное пособие. − Омск: Издательство ОмГПУ, 1997. – 149с.: ил. -70, таб. 9.
5. Дороднов А.М., Острецов И.Н., Петросов В.А. Графики функций. Учеб. пос. для пост. в вузы-М.: Высшая школа,1972.
6. Зубкова Л. Н. Урок-семинар по теме «Производная и ее применение», Журнал «Математика в школе» №6, с.57-59.
7. Методика преподавания математики в средней школе: Частная методика: Учеб. Пособие для студентов пед. институтов по физ.-мат. Спец. / А. Я. Блох, В. А. Гусев, Г. В. Дорофеев и др.; Сост. В. И. Мишин. − М.: Просвещение, 1987. – 416с.
8. Саакян С. М., Дудницын Ю. П. Примерное планирование учебного материала по математике в 10-11 классах, Журнал «Математика в школе» №7, с.2-5.
9. Тульчинская Е. Е. Поурочное планирование и контрольные работы по алгебре и началам анализа, Журнал «Математика в школе» №10, с.27.
10. Электронный ресурс: http://freemath.ru/load/shkolnaja_matematika
|